Buck-boost变换器的建模与控制 第二次作业

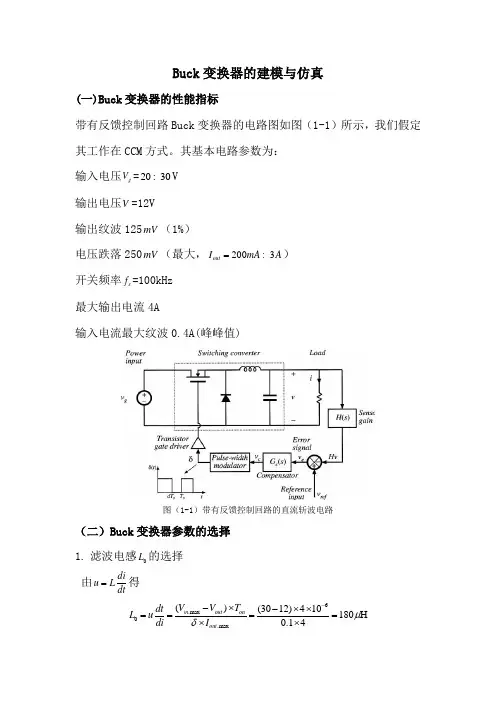
Buck 变换器的建模与仿真(一)Buck 变换器的性能指标带有反馈控制回路Buck 变换器的电路图如图（1-1）所示，我们假定其工作在CCM 方式。

其基本电路参数为： 输入电压g V =2030V 输出电压V =12V 输出纹波125mV （1%）电压跌落250mV （最大，2003out I mA A =） 开关频率s f =100kHz 最大输出电流4A输入电流最大纹波0.4A(峰峰值)图（1-1）带有反馈控制回路的直流斩波电路（二）Buck 变换器参数的选择 1. 滤波电感0L 的选择 由diu Ldt=得 6.max 0.max ()(3012)410180H 0.14in out on out V V T dt L u di I μδ--⨯-⨯⨯====⨯⨯这里我们取0L 为180H μ 最大负载时的峰值电流为.max .max 40.054 4.22peak out out I I I A δ=+=+⨯=2. 滤波电容0C 的选择 由dui cdt=得 其向量形式为I j cU ω=I jcUω=所以需要穿越频率的带宽为2outc out outI f C V π∆=∆如果假定穿越频率为10kHz250892.8out c out V mZ m I ∆===Ω∆ 原则上为了留有设计裕量，电阻的阻抗按13计算阻抗选取 根据上面计算结果，我们可以在Rubycon 公司的ZL 系列，16V 中选取以下规格：C=330F μ,760C rms I mA =@105A C =︒ ,72ESR low R m =Ω@20A T C =︒ ,220ESR low R m =Ω@10A T C =-︒电容ESR 的阻抗应小于输出电容在穿越频率处的阻抗11482 6.2810330c out m f C k π==Ω⨯⨯86c Z m ≤==Ω设计余量不足，我们重新选ZL 系列中C=1000F μ，同样的过程，我们可以得出满足条件。

用状态空间平均法为buck -boost 变换器建模选取了状态空间平均法为电路建模，当变换器满足低频假设和小纹波假设时，对于状态变量与输入变量可以用一个开关周期内的平均值代替瞬时值，并近似认为平均值在一个开关周期内维持恒值。

这种方法使不同结构的变换器的解析模型有了统一的形式。

DCM 模式下，buck -boost 电路比CCM 模式多了一种工作状态。

一、列写状态方程和电感电流平均变量方程 1. 工作状态1 开关管导通，二极管截止 设状态变量()()()i t x t v t ⎡⎤=⎢⎥⎣⎦，()i t 为电感电流，()v t 为输出电压 输出变量()()g y t i t ⎡⎤=⎣⎦，()g i t 为输入电流 输入变量()()g u t v t ⎡⎤=⎣⎦，()g v t 为输入电压inVR根据电路图，变换器的状态方程和输出方程如下：()001()()1()()00g di t i t dt v t L dv t v t RC dt ⎡⎤⎡⎤⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦[]()()100*()()g g i t i t v t v t ⎡⎤=+⎢⎥⎣⎦则10010A RC ⎡⎤⎢⎥=⎢⎥-⎣⎦，110B L ⎡⎤⎢⎥=⎢⎥⎣⎦，[]110C =，[]10E = 2. 工作状态2 开关管截止，二极管导通inVR变换器的状态方程和输出方程如下：[]()10()0()11()()g di t i t dt L v t dv t v t C RC dt ⎡⎤⎡⎤-⎢⎥⎢⎥⎡⎤=+⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦ []()()000*()()g g i t i t v t v t ⎡⎤=+⎢⎥⎣⎦则21011L A C RC ⎡⎤-⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦，[]20B =，[]200C =，[]20E = 3. 工作状态3 开关管和二极管都截止inV R变换器的状态方程和输出方程如下：()00()0()1()()00g di t i t dt v t dv t v t RC dt ⎡⎤⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎢⎥⎣⎦⎢⎥⎣⎦[]()()000*()()g g i t i t v t v t ⎡⎤=+⎢⎥⎣⎦则30010A RC ⎡⎤⎢⎥=⎢⎥-⎣⎦，300B ⎡⎤=⎢⎥⎣⎦，[]300C =，[]30E =列写电感电流平均变量方程()1()()()2sTs g Ts Ts d T i t v t v t L<>=<>-<> 上式为电感电流在12[0,()]s d d T +时间段内的平均电感电流二、求静态工作点和D23121D D D =--根据分阶段列写的状态方程与输出方程可得到2112233201D L A D A D A D A D C RC ⎡⎤-⎢⎥=++=⎢⎥⎢⎥-⎢⎥⎣⎦ 11122330D B D B D B D B L ⎡⎤⎢⎥=++=⎢⎥⎣⎦[]11223310C DC D C D C D =++= []1122330E D E D E D E =++=根据0AX BU Y CX EU+=⎧⎨=+⎩，可以得到变换器的稳态方程组2120010g D D I LV L D V CRC ⎡⎤-⎡⎤⎢⎥⎡⎤⎢⎥+=⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥-⎣⎦⎢⎥⎣⎦ []100*g g I I D V V ⎡⎤=+⎢⎥⎣⎦12sg D T I V L=从上式可得210g D V DV -+=20VD I R-= 可以得到用1D 和2D 表示的变比M12g D VM V D == 可以解得未知量2D 、I 、g I 和变比M21122sg D L K RT M I DV I D I D R =======当变换器运行在闭环情况下，M 、K 、V 已知，因此将1D 和2D 、I 表达为M 、K 、V 的函数更便于确定系统的控制策略。

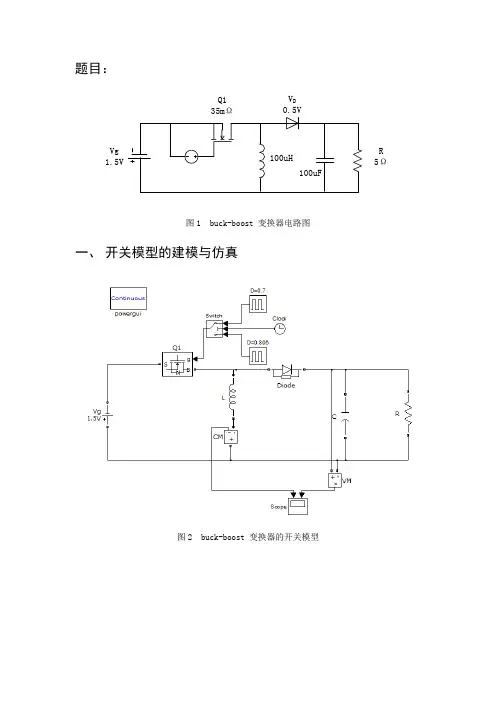
题目：Vg 1.5VQ135m Ω100uH100uFR5ΩV D0.5V图1 buck-boost 变换器电路图一、开关模型的建模与仿真图2 buck-boost 变换器的开关模型占空比由0.806变化到0.7的电感电流波形占空比由0.806变化到0.7的电容电压波形图3 buck-boost 变换器的开关模型的仿真二、 大信号模型与仿真1、 开关导通时：Vg 1.5VR on35m ΩV-图4 开关导通时的工作状态此时，电感电压和电容电流方程：(t)v (t)v (t)(t)(t)(t)(t)L g on c di L i R dt dv v i C dt R ⎧==-⎪⎪⎨⎪==-⎪⎩2、 开关断开时：100uH100uFVi c+-0.5Vi图5 开关断开时的工作状态此时，电感电压和电容电流方程：(t)v (t)(t)(t)(t)(t)(t)L D c di L V v dt dv v i C i dt R ⎧==--⎪⎪⎨⎪==-⎪⎩3、平均方程电源电压、电感电流、电容电压变化的不大均为低频信号，则(t)(t)g g v v = ；(t)(t)i i =；v(t)v(t)=又因为：(t)v (t)L d i L dt= (t)(t)c d v i Cdt= 则有，电感电压平均方程：()()'v (t)d(t)v (t)(t)+d (t)(t)L g on D i R V v =---电容电流平均方程：''(t)(t)(t)(t)d(t)()d (t)((t))=d (t)(t)c v v v i i i R R R=-+--+ 输入电流平均方程：g (t)d(t)(t)i i =4、大信号模型：()()''g (t)d(t)v (t)(t)+d (t)(t)d (t)(t)=d (t)(t)(t)d(t)(t)g on D d i L i R V v dt v v C i dt R i i ⎧=---⎪⎪⎪-+⎨⎪⎪=⎪⎩由方程可得到三个等效电路：-+-+-+g (t)i v (t)g (t)v D (t)i 'D (t)i d (t)v Cdt(t)d i Ldt'(0.5D )VonDR '(t)D v v (t)g D 图6 buck-boost 变换器的大信号模型的等效电路大信号模型的仿真电路：图7 大信号模型仿真电路图大信号模型的仿真波形：占空比随时间变化的波形电容电压随占空比变化的波形图8 大信号模型仿真波形图三、 小信号模型假设，gv (t)=V +v (t)d(t)=D+d(t)(t)=(t)v(t)=V+v(t)(t)=(t)g g g g g i I i i I i ΛΛΛΛΛ⎧⎪⎪⎪⎪⎨+⎪⎪⎪⎪+⎩ 且各变量的扰动值远小于其稳态值。

DC―DC开关变换器的建模与非线性行为控制一、Buck-Boost变换器工作原理Buck-Boost变换器电路如图1（a）所示。

Buck-Boost变换器功率级工作原理：当功率开关管S导通时，二极管D受反向电压关断，电感电流>上升。

当上升达到参考电流I时，S断开，>通过D进行续流，此时D导通。

如果在下一个时钟脉冲到来时大于0，则电路工作于连续导电模式（CCM），电路波形图1（b）所示；如果在下一个时钟脉冲到来前已降到0，则电路工作于不连续导电模式（DCM），此时开关S和D都关断，电路波形图1（c）所示。

控制级工作原理：将电感电流的采样值与参考电流I输入比较放大器A（其放大系数为K），得到误差信号e=（I-），该误差信号与锯齿波信号相比较，控制输出信号调节占空比D，进而控制开关S的导通时。

二、Buck-Boost变换器非线性行为在进行Buck-Boost变换器非线性行为分析前，做如下假设：（1）负载上的电压V恒定不变，可看作是一个电压源。

在实际电路中只要滤波电容足够大，这一假设是成立的；（2）变换器中所有器件均为理想器件，忽略其寄生参数。

1、连续导电模式在t=t（n=0，1，2，…）时刻，S闭合。

此时系统的微分方程为：（1）在t=t+DT（n=0，1，2，…）（D为系统的占空比）时刻，S 断开，此时系统的微分方程为：（2）当电感电流达到参考电流值时，电路开关S由导通转换为关断。

电感电流在时刻的采样值与基准电流I输入比较器A，A的反馈倍数为K，系统的采样控制方程为：（3）en输入PWM控制器，与锯齿波相比较，形成的占空比规律如下：（4）采用A开关映射的数据采样方法，即在开关S闭合的时刻采样数据。

设在t=tn（n=0，1，2…）和t=tn+T （n=0，1，2…）时刻电感电流采样值分别为in，in+1，则系统的离散方程为：（5）将式（3）和式（4）代入式（5），得：（6）其中：式（6）即为系统CCM的离散迭代方程。

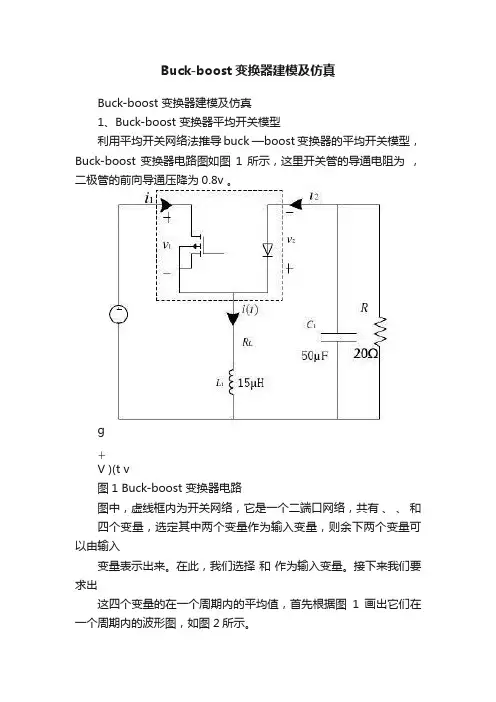
Buck-boost变换器建模及仿真Buck-boost 变换器建模及仿真1、Buck-boost 变换器平均开关模型利用平均开关网络法推导buck —boost 变换器的平均开关模型，Buck-boost 变换器电路图如图1所示，这里开关管的导通电阻为，二极管的前向导通压降为0.8v 。

gV )(t v图1 Buck-boost 变换器电路图中，虚线框内为开关网络，它是一个二端口网络，共有、、和四个变量，选定其中两个变量作为输入变量，则余下两个变量可以由输入变量表示出来。

在此，我们选择和作为输入变量。

接下来我们要求出这四个变量的在一个周期内的平均值，首先根据图1画出它们在一个周期内的波形图，如图2所示。

)(1t v s dT sT (1i sdT s)(1t i )(2t i )(1t v on R )(2t v )(1t i )(2t v图2 开关网络电压电流的曲线图根据图2，写出)(1t i 、)(2t i 、)(1t v 、)(2t v 在一个周期内平均值：（1）（2）（3）（4）由式（3）与（4）得（5）将公式（1）与（5）代入（3）中得（6）将公式（6）中两边的)(1t v 合并得到下面式子：（7）由（1）与（2）得（8）])([)()(')()()(211D T T on T V t v t d t d t i t d R t v s s s +><+><=><= ><)()()(')(12(2vD(2t i ss s T T t i t d t i ><=><)()()(1s s T T t i t d t i ><=><)()(')(2))()((')()()(11s s s T C D g on T T t V V V t d R t i t d t v ><-++><=>s +><+><+>=<><由式（7）（8）可以得到开关网络的平均开关模型，如图3所示：图3 平均开关模型把图1中的开关网络用图3所示的平均开关模型代替可得到图4所示的Buck-boost 变换器的开关模型电路。

实验一：Buck-Boost变换器状态空间平均模型建模（一）实验目的1.掌握Matlab的程序编程2.掌握电力电子变换器的状态空间平均建模（二）实验原理1．升降压斩波电路原理图1.升降压斩波电路原理图该电路的基本工作原理：当可控开关V处于通态时，电源E经V向电感L供电使其储存能量，此时电流为i1。

同时，电容C维持输出电压基本恒定并向负载R供电。

此后，使V关断，电感L储存的能量向负载释放，电流为i2。

当V处于通态期间，u L=E；而当V处于断态期间，u L=u0。

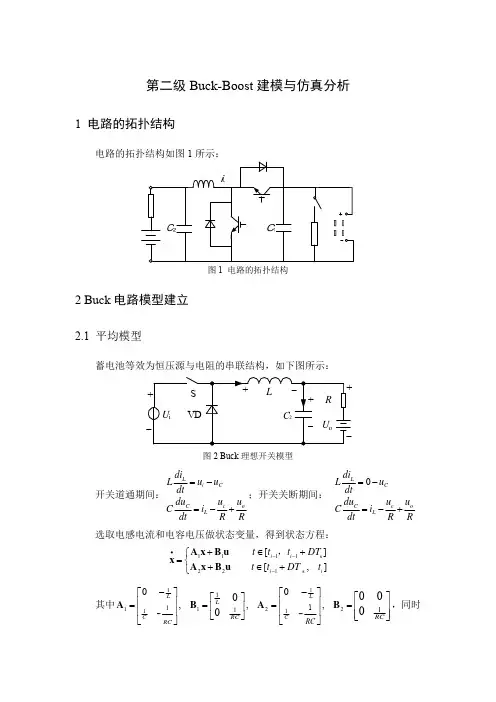
于是，Et on=U0t off，所以输出电压为U0=t ont offE=α1−αE由EI1=U0I2，得出输出电流为I2=1−ααI12.状态空间平均法的原理状态空间平均法是平均法的一阶近似，其实质为：根据线性RLC元件、独立电源和周期性开关组成的原始网络，以电容电压、电感电流为状态变量，按照功率开关器件的“ON”和“OFF”两种状态，利用时间平均技术，得到一个周期内平均状态变量，将一个非线性电路转变为一个等效的线性电路，建立状态空间平均模型。

对于不考虑寄生参数的理想PWM变换器，在连续工作模式（CCM）下一个开关周期有两个开关状态相对应的状态方程为：ẋ=A1x+B1v i，0≤t≤dTẋ=A2x+B2v i，dT≤t≤T式中d为功率开关管导通占空比，d=t on/T，t on为导通时间，T为开关周期；x=[i L u C]，x是状态变量，ẋ是状态变量的导数，i L是电感电流,u C是电容电压，E是开关变换器的输入电压；A1,A2,B1,B2是系数矩阵,与电路的结构参数有关。

对上式进行平均得到状态平均方程为ẋ=Ax+Bv i，A=d A1+(1-d)A2, B=d B1+(1-d)B2,这就是著名的状态空间平均法。

可此式可见，时变电路变成了非时变电路，若d为常数，则这个方程描述的系统是线性系统，所以状态空间平均法的贡献是把一个开关电路用一个线性电路来替代。

1 概述直流-直流变流电路的功能是将直流电变为另一固定电压或可调电压的直流电，包括直接直流变流电路和间接直流变流电路。

其中，直接直流变流电路又叫斩波电路，它包括降压斩波电路（Buck Chopper）、升压斩波电路（Boost Chopper)、升降压斩波电路（Buck/Boost）、Cuk斩波电路、Sepic斩波电路和Zeta斩波电路共六种基本斩波电路。

Buck/Boost升降压斩波电路同时具有Buck斩波电路和Boost斩波电路的特点，能对直流电直接进行降压或者升压变换，应用广泛。

本文将对Buck/Boost升降压斩波电路进行详细的分析。

RVDRVDRVD2 主电路拓扑和控制方式Buck/Boost 主电路的构成Buck/Boost 变换器的主电路与Buck 或Boost 变换器所用元器件相同，也由开关管、二极管、电感、电容等构成，如图1所示。

与Buck 和Boost 不同的是电感L 在中间，不在输出端也不在输入端，且输出电压极性与输入电压极性相反。

开关管也采用PWM 控制方式。

Buck/Boost 变换器也由电感电流连续和断续两种工作方式，但在实际应用中，往往要求电流不断续，即电流连续，当电路中电感值足够大时，就能使得电路工作在电流连续的状态下。

因此为了分析方便，现假设电感足够大，则在一个周期内电流连续。

图2-1 Buck/Boost 主电路结构图电流连续时有两个开关模态，即V 导通时的模态1，等效电路见图2（a ）；V 关断时的模态2，等效电路见图2（b ）。

（a ）V 导通（b）V关断，VD续流图2-2 Buck/Boost不同模态等效电路ttttt电感电流连续时的工作原理及基本关系电感电流连续工作时的工作主要波形见图2-3。

图2-3电感电流连续时的主要波形为了方便分析，假设电感、电容的值足够大，并且忽略电感的寄生电容。

电感电流连续工作时，Buck/Boost 变换器有V 导通和V 关断两种工作模态。

一种四开关buck-boost变换器的控制电路及控制方法-概述说明以及解释1.引言1.1 概述概述:四开关buck-boost变换器是一种常用的电力电子变换器，具有宽电压输入范围和高效率的特点。

本文旨在介绍一种针对四开关buck-boost 变换器的控制电路及控制方法，以优化其性能和稳定性。

通过对该变换器的介绍、控制电路设计和控制方法分析，我们将展示该变换器在电能转换和控制方面的重要性和潜力。

通过本文的阐述，读者将对四开关buck-boost变换器有更深入的了解，并对其在实际应用中具有的优势有更清晰的认识。

1.2 文章结构文章结构部分是对整篇文章的内容进行简要介绍，提供读者一个整体的框架和概念。

在这篇文章中，我们首先介绍了引言部分，其中包括概述、文章结构和目的。

接着我们将详细讲解正文部分，包括四开关buck-boost 变换器的介绍、控制电路设计和控制方法分析。

最后我们将总结这篇文章，展望其创新性，探讨其应用前景。

整篇文章将从理论到实践，全面介绍一种四开关buck-boost变换器的控制电路及控制方法。

1.3 目的:本文旨在研究一种四开关buck-boost变换器的控制电路及控制方法，通过对该变换器的性能进行分析和优化，提高其效率和稳定性。

通过对控制电路的设计和控制方法的分析，我们将深入探讨该变换器在不同工况下的工作原理，为其在实际应用中提供更好的指导和参考。

同时，通过这项研究，我们也希望能够为电力电子领域的技术发展和应用提供一定的借鉴和启示，推动相关技术的进步和发展。

最终，我们的目的是通过这篇文章对四开关buck-boost变换器的控制进行深入研究，为相关领域的研究人员和工程师提供有益的参考和启示，推动电力电子技术的不断创新和进步。

2.正文2.1 四开关buck-boost变换器介绍四开关buck-boost变换器是一种高效率、高性能的DC-DC变换器，可以实现输入电压向上或向下转换为稳定的输出电压。