下载文档原格式
第1章绪论
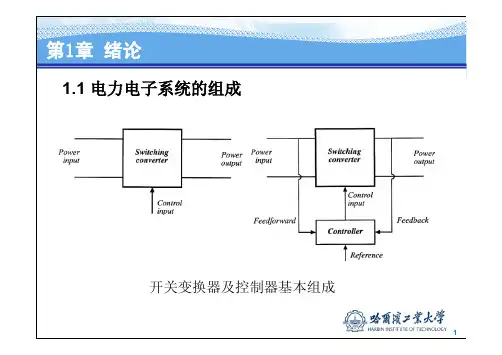
1.1 电力电子系统的组成
1.1 电力电子系统的组成
1.1 电力电子系统的组成
1.1 电力电子系统的组成
1.1 电力电子系统的组成
1.1 电力电子系统的组成
1.2 电力电子系统建模目的
1.2 电力电子系统建模目的
1.3 电力电子电路模型分类与建模方法
1.3 电力电子电路模型分类与建模方法
1.3 电力电子电路模型分类与建模方法
型
1.3 电力电子电路模型分类与建模方法
1.3 电力电子电路模型分类与建模方法
1.3 电力电子电路模型分类与建模方法
1.3 电力电子电路模型分类与建模方法
1.4 电力电子电路建模特点建模过程：
1.4 电力电子电路建模特点
．器件模型的适用性
1.5 电力电子系统仿真技术的发展
1.5 电力电子系统仿真技术的发展
More automation
自动化流水生产线
Automatic Assembly Line
1.6 本课程关注的焦点
教学安排
教学安排。
无穷大功率电源供电系统仿真假设无穷大功率电源供电系统，在0.02s时刻变压器低压母线发生三相短路故障，仿真其短路电流周期分量幅值和冲击电流的大小。
线路参数L=50km，x1=0.4Ω/km，r1=0.17Ω/km；变压器Sn=20MV·A，短路电压Us%=10.5，短路损耗ΔPs=135kw，空载损耗ΔP0=22kw，空载电流I0%=0.8，变比kT=110/11，高低压绕组均为Y行联接；并设供电点电压为110KV。
其对应的Simulink仿真模型如图1-1所示。
图1-1 无穷大功率电源供电系统的Simulink仿真图表1-1 图1-1仿真电路中各模块名称及提取路径模块名提取路径无穷大功率电源Three-Phase Source SimPowerSystems/Eletrical Sources三相并联RLC负荷模块5MW SimPowerSystems/Elements串联RLC支路Three-phaseParallelRLCBranch SimPowerSystems/Elements三相故障模块Three-phase-Fault SimPowerSystems/Elements三相电压电流测量模块V-I-M SimPowerSystems/Measurements示波器模块Scope Simulink/Sinks电力系统图形用户界面Poweigui SimPowerSystems双绕组变压器模块Three-PhaseTransformer SimPowerSystems/Elements图1-2 电源模块的参数设置变压器T 采用“Three-PhaseTransformer （Two Windings ）”模型。
根据给定的数据，计算折算到110kv 侧的参数如下：变压器的电阻为2233221351101010 4.0820000s N T N PU R S ∆⨯=⨯=⨯Ω=Ω 变压器的电抗为22332%10.5110101063.5310010020000s N T N U U X S ⨯=⨯=⨯Ω=Ω⨯ 变压器的漏感：63.53/(2)0.2022 3.1450T T L X f H H π===⨯⨯变压器的励磁电阻为2233301101010 5.51022N m U R P =⨯=⨯Ω=⨯Ω∆ 变压器的励磁电抗为22330100100110101075625%0.820000N m N U X I S ⨯=⨯=⨯Ω=Ω⨯ 变压器的励磁电感为75625/(2)240.82 3.1450m m L X f H H π===⨯⨯变压器模块中的参数采用有名值则设置如图1-3所示图1-3采用有名值时变压器模块的参数设置如果要采用标幺值，则在Similink 的三相变压器模型中，一次、二次绕组漏感和电阻的标幺值以额定功率和一次、二次侧各自的额定线电压为基准值，励磁电阻和励磁电感以额定功率和一次额定线电压为基准值。
电力电子器件的建模与控制随着电力电子技术的不断发展，电力电子器件在工业、航空、船舶、军事等领域中的应用日益广泛。
电力电子器件的建模与控制是电力电子技术的重要研究方向。
本文将从建模与控制两个方面对电力电子器件进行探讨。
一、电力电子器件的建模建立电力电子器件的数学模型是研究电力电子器件必不可少的一步。
通过建模，可以分析电路的性能、控制器的设计和控制策略的优化。
下面将介绍常用的电力电子器件的建模方法。
1.硅控整流器模型硅控整流器是一种常见的电力电子器件。
硅控整流器的模型可使用平均值模型来建立。
该模型假设输电电压和输出电流是恒定的，并考虑了开关器件的导通与关闭时间。
该模型的参数包括输入电压、输出电流、开关器件的电阻和电容等参数。
2.IGBT模型IGBT是一种常见的功率晶体管。
IGBT的模型可使用双极性晶体管模型来建立。
该模型假设管子中的电荷可以被充电和放电，并将管子的行为分为两个状态：导通状态和截止状态。
该模型的参数包括输电电压、支路电阻、门控电源电压、漏极电流等参数。
3.电容模型电容是一种基本的电力电子器件。
电容的模型可以使用电容模型来建立。
该模型假设电容器可以储存电荷，并导致电势差的变化。
该模型的参数包括电容量、电势差、储能能量等参数。
二、电力电子器件的控制通过控制器对电力电子器件进行控制，可以实现对电路的控制和优化。
在控制器的设计与开发过程中，我们通常需要考虑以下三个方面的内容：1.控制器的输出控制器的输出是控制电路的关键。
输出应具有良好的稳定性和准确性，并且应相应地响应输入信号。
2.控制器的输入控制器的输入是从传感器、计算机或其他控制器获得的信号。
输入信号应被正确识别和处理，并被传递给控制器以支持合理的控制策略。
3.控制器的策略为实现良好的控制性能，必须实施合理的控制策略。
控制策略应该基于目标性能指标，例如输出电流和功率，恰当地融合传感器技术、控制算法和装置等。
总结电力电子器件的建模与控制是电力电子技术发展的关键。
《电力电子仿真技术》大作业一、（20分）单相桥式不可控整流电路仿真。
1、实验目的：掌握单相桥式不可控整流电路在电阻电感负载时的工作2、实验要求：交流电压220V（有效值），50Hz，直流侧滤波电容1000微法。
负载电阻10欧姆，10毫亨。
3、实验内容：（1）搭建电路模型（5分）。
电源参数（2）记录负载电压和电容电流波形（5分）。
（3）搭建二极管额定电流计算子系统，显示二极管额定电流计算结果（10分）。
分析：二极管电流对时间积分后除以二极管导通的时间求得二极管额定电流子系统如下：考虑到仿真时间为0.1，而二极管导通时间为其一半，所以导通时间为0.05子系统接入总电路后的图如下：额定电流为26.154、实验结果分析实验能看出单相桥式不可控整流电路仿真的自然换相点以及计算算出二极管的额定电流二、（20分）单相桥式可控整流电路仿真。
1、实验目的：掌握单相桥式可控整流电路仿真，并观察各个器件的波形以了解其工作原理。
2、实验要求：交流电压220V（有效值），50Hz。
负载电阻10欧姆，10毫亨。
3、实验内容（1）搭建触发信号子系统，显示触发信号。
脉冲信号一参数设置为脉冲信号二参数设置相位相差180度（2）搭建电路模型（5分）。
（3）记录晶闸管电压和电流波形（5分）。
（4）画出负载电压平均值随控制角的变化曲线（10分）。
4、实验结果分析：仿真波形与理论分析一致三、（20分）三相桥式可控整流电路仿真。
1、实验目的：通过三相桥式可控整流电路仿真了解电路原理以及加深印象。
2、实验要求：交流相电压220V（有效值），50Hz。
变压器漏感为5毫亨。
负载电阻10欧姆，10毫亨，反电势400V。
控制角120度。
3、实验内容：（1）搭建电路模型（5分）（2）记录负载电压和电流波形（5分）。
（3）搭建换相压降计算子系统，显示换相压降计算结果（10分）。
换相压降=3/2πXI负载电流平均值计算换相压降计算结果：有问题。
四、（20分）升降压直流斩波电路仿真。
上海电机学院卢昌钰 BG0801 10号1.单相半波可控整流电路（1）电阻性负载（R=1欧姆，U2=220V,α=30°）接线图电阻性负载二次电压，输出电压，二次电流，输出电流，晶闸管电压曲线输入电压与输出电压波形（2）阻感负载（R=1欧姆，L=0.05H，U2=220V,α=30°）接线图阻感负载二次电压，输出电压，二次电流，输出电流，晶闸管电压曲线输入电压与输出电压波形（3）阻感负载+续流二极管（R=1欧姆，L=0.05H，U2=220V,α=30°）有问题接线图阻感负载二次电压，输出电压，二次电流，输出电流，晶闸管电压曲线输入与输出电压波形2.单相桥式全控整流电路（1）电阻性负载（R=1欧姆，U2=220V,α=60°）电阻性负载电路图搭建电阻负载输入电压和输出电压对比电阻负载直流电压和电流波形电阻负载时晶闸管T1的波形电流i2的曲线（2）电感性负载（R=1欧姆，L=0.05H,α=60°，U2=220V,）阻感负载电路图搭建阻感负载电压输入与输出波形阻感负载输出电流id阻感负载输出电压ud阻感负载交变时的电流i2阻感负载交变时的电压u2阻感负载VT1的电压波形（3）电感性负载+续流二极管（R=1欧姆，L=0.05H,α=60°，U2=220V,）电感性负载+续流二极管接线图输入和输出电压波形负载电流负载电压二次侧电流晶闸管两端电压3.单相桥式半空整流电路（1）电阻负载（R=1欧姆，α=60°，U2=220V,）接线图二次侧电压，负载电压，二次侧电流，负载电流，晶闸管电压，二极管电压，二极管电流波形图（2）阻感负载（R=1欧姆，L=0.05H，α=60°，U2=220V,）接线图二次侧电压，负载电压，二次侧电流，负载电流，晶闸管电压，二极管电压，二极管电流波形图（3）阻感负载+续流二极管（R=1欧姆，L=0.05H，α=60°，U2=220V,）接线图二次侧电压，负载电压，二次侧电流，负载电流，晶闸管VT1电压，二极管VD4电压，二极管VD4电流波形图4.三相半波可控整流电路电阻负载接线图（0°）三相输入电压输出电流和电压晶闸管1的电流电压输出波形（电阻0°）三相输入电压输出电流和电压晶闸管1的电流电压输出波形（电阻30°）阻感负载接线图（30°）三相输入电压输出电流和电压晶闸管1的电流电压输出波形（阻感30°）阻感负载+续流二极管接线图（30°）5．三相全控整流电路电阻负载接线图（30°导通角）三相输入输出电压对比，晶闸管1电压，输出电流电压图形（30°）阻感负载接线图（30°导通角）三相输入输出电压对比，晶闸管1电压，输出电流电压图形（30°）阻感负载+续流二极管接线图（30°导通角）6 降压BUCK电路降压斩波电路（电流连续）接线图BUCK变换器电感电流连续时仿真波形BUCK变换器电感电流断续时仿真波形7 升压Boost电路升压Boost变换器仿真接线图升压Boost变换器连续工作升压Boost变换器断续工作8 单相全桥方波逆变电路单相全桥方波电阻负载逆变电路接线图电阻负载逆变器直流侧电流，输出交流电压电流方波波形单相全桥方波阻感负载逆变电路接线图阻感负载逆变器直流侧电流，输出交流电压电流方波波形9 三相方波逆变电路三相方波逆变电路接线图三相方波逆变电路仿真波形（感性无功=100Var）10单极性的PWM方式下的单相全桥逆变电路在下：输出电压，电流和直流侧电流波形。
三相桥式电压型逆变器电路的建模与仿真实验摘要：本文在对三相桥式电压型逆变电路做出理论分析的基础上，建立了基于MATLAB的三相桥式电压型逆变电路的仿真模型并对其进行分析与研究，用MATLAB 软件自带的工具箱进行仿真，给出了仿真结果，验证了所建模型的正确性。
关键词：逆变；MATLAB；仿真第一章概述1.1电力电子技术顾名思义，可以粗略地理解，所谓电力电子技术就是应用于电力领域的电子技术。
电子技术包括信息电子技术和电力电子技术两大分支。
通常所说的模拟电子技术和数字电子技术都属于信息电子技术。
电力电子技术中所变换的"电能"和"电力系统"所指的"电力"是有一定差别的。
两者都指"电能"，但后者更具体，特指电力网的"电力"，前者则更一般些。
具体地说，电力电子技术就是对电能进行变换和控制的电子技术。
更具体一点，电力电子技术是通过对电子运动的控制对电能进行变换和控制的电子技术。
其中，用来实现对电子的运动进行控制的器件叫电力电子器件。
目前所用的电力电子器件均由半导体材料制成，故也称电力半导体器件。
电力电子技术所变换的"电力"，功率可以大到数百兆瓦甚至吉瓦，也可以小到数瓦甚至是毫瓦级。
信息电子技术主要用于信息处理，而电力电子技术则主要用于电力变换，这是二者本质上的不同。
1.2电力电子技术的应用（1）一般工业中，采用电力电子装置对各种交直流电动机进行调速，一些对调速性能要求不高的大型鼓风机近年来也采用变频装置以达到节能的目的，除此之外，有些对调速没有特别要求的电机为了避免启动时的电流冲击而采用软启动装置，这种软启动装置也是电力电子装置。
电化学工业大量使用直流电源，电解铝、电解食盐水以及电镀装置均需要大容量整流电源。
电力电子产品还大量应用于冶金工业中的高频或中频感应加热电源、淬火电源及直流电弧炉电源等场合。
电力电子建模与控制基于BUCK变换器反馈控制设计专业：电气工程姓名：________ 荏学号：13S053072BUCK 变换器反馈控制设计第一部分：设计目标图1 Buck 变换器系统根据给定的条件，要求完成以下设计任务：1•建立系统的传递函数TF ;2. 给定参数：主电感 L 50 H R C 0.05 ,V g 30V V 。
15V ，R 5 C 100 F ,R 0 。
设计补偿网络Gc(s);3. 画出补偿前后系统传递函数的bode 图；4. 讨论补偿传递函数Gc(s)对于系统零点、极点、输出调节、输出阻抗及对 系统动态性能的影响。
第二部分：传递函数的建立与仿真、系统开环传递函数建立:图2统一电路模型对于给定的buck 变换器电路，如图1所示。
|«|表1 BUCK 变换器统一电路模型参数i)1. BUCK 变换器占空比至输出传递函数 G vd (s):由以上模型和参数课求得占空比至输出的传递函数 G vd (s):2. 主拓扑参数选择:本文控制系统中反馈电阻选择：R X 1bbk ,R y 1bbk ，即反馈系数 1H(s)孑开关频率为f s 1bbkHz ，参考电压为5V ，锯齿波幅值3V 。
3. 工作方式：根据BUCK 变换器电流连续与断续状态的临界电感公式为1 D?V g D 2T sD ?利用Matlab 软件画出G b (s)的bode图，如图3所示，从图中可以看出，系 统的幅值裕度无穷大，然而，相角裕度比价小，只有Pm=15.7deg 不符合系统的要求。
CgnwTWC,V g (R sR c RC)G vd (s)R (L R c RC) s LC (R R c ) s 2(1)1crit2L代入给定的参数值，可知, 电感电流 I I crit ，电路工作在连续CCM 模式。
二、补偿前系统传递函数bode 图1•原始回路增益函数G 0(s)G b (s) H(s)G.(s)G vd (s) V g (R sRRC& RV m 1 s(R F C RC s 2LC(R R)(3)代入相应数值后 100 1 100 1OO 32.补偿前系统传递函G b (s)530(5 2.5 10 s)5 7.5 10 5s 25.25 10 9s 2bode 图 5 2.5 10 5s1 1.5 10 5s 5.05 109s 2三、系统时域内实时仿真□Ucret 曰Tm = Le-[J7 5.Flp=i 阻 Tgiii图4 BUCK 主电路实时仿真图 对应的仿真波形图如图5所示：从仿真波形中可以看出，系统的动态特性较差，存在较大的输出超越量和较长的 调节时间，稳态时，输出结果并非精确的15V ，故存在较大的稳态误差。
通常选 择相位裕度在45度左右，增益裕度在10dB 左右，因此需要加入补偿网络Gc(s)，3txJe D 购 idTHGm = Inf Pm = 157 deg (at 346e 104 rad*sj§p- S H 图3补偿前系统开环系统bode 图利用matlab/Simulink 中相关的模块，搭建开环实时仿真电路图 ，如图 4所示:Pul 笙GsH&alSfMosfet亠.——E 十S[ D 4+30VRLV M图中黑色线条代表输出电压波形，紫红色代表流过电感的电流波形，黄色为矩形波发生器波形。
取其中一小段观察，如图6所示:图6稳态时系统波形图第三部分：补偿网络的设计一、补偿器传递函数(4)图1中所示的补偿器网络为一种有源超前--滞后补偿网络，其传递函数为匚(訂価恃)■ ™■—i lO ()〃( R、+ 点)(1 + s??2 G)[1 + *(R] + 尺、)Cj j［州(c, ++ 尤t * g 3有源趙审J 二滞后补fS 网培二右两个零点，二个极点. 零点为：Alh 知2乙G 人=驾"咅(&：比)-东屆根点为：A ，M 碧=0.为虞乩厶=¥ = 2聞二"厂書二—K T C T Q2n■^^sass^ _______________ •一工靠a.A这里 R 3 R 1 ,C 2 C 1。
二、补偿器设计方法1.采用推荐公式f g f s /5即f g 20kHz ，f s 为BUCK 变换器的开关频率，一般说来，补偿后的回路函数f g 越大，变换器的动态速度越快。
从bode 图中可以看出，原始回路函数G 0(s)有两个相近的极点，极点的频率 为f p1,p21/(2 J L C) 2.25 103H Z ，可将补偿网络GJs)两个零点设计为原始回1路函数G o (s)两个相近的极点频率的1/2,即f z1 f z2 ^f pw 1.2 始回路函数G o (s)有一个零点，这是由于输出滤波电容的等效串联电阻2.零极点确定 103H Z 。
原 Rc 引起 的，此时可用补偿网络的极点来补偿，令 G c (s)的极点f p2 "ZESR 5f p3 10f s两个零点：f zi f Z 2£f p1,p2 1.2 103H Z ； 三个极点：f pi 0，P1 f p2f ZESR 32kHz ，f p3 10f p1 22.5kHz 。
3.补偿网络G c(s)参数求取(4)4.补偿网络G c (s)的bode 图G c (s)的表达式为:(1 1.3 104s)2cks ：1 5 106s)(1 7 106s)(5)其中 k R i (C i C 2)。
原始回路函数G 0(s)在f g 的增益为:G o (j2 f g )1 1.2 10 55 2.5 10 5j2 f gj2 f g5.05 10-9(j2f g )20.075补偿网络G c (s)在f g 的增益为:G c (j2 f g )13.3零点f zl 、f z2处的增益为:AVfz2极点f p2的增益为:G o (j2 f g )G c (j2 f g ) -^200^133M 闕20荷0.8fp2fg求取补偿网络电路各元件的参数: AV 2R LR3G c (j2 f g32^03 13.320 1c 321.3假设R 210k ，可得 R 3R 2 AV 24702 f z1R 20.013 FC3—1—0.01 F2 f p2R 3C2—1—707pF 2 f RR 11 2 f z2C 313.3ks(1 5 106s)(1 7 10 6s) s1.2 105s 2 3.5 10"1s 3对应的bode 图：'七一-图7补偿网络G c （s ）的bode 图第四部分：补偿后系统性能分析一、补偿后系统的bode 图1.补偿后系统传递函数为G(s) G c (s) G 0(s)2.补偿后系统的bode 图:5 25800 1.58 s 9.8 10 s 一，、5800 (1 1.3 104s)2G c (s),1 ■ ! I =-.Jrt. ~-r IM j "Tin討「■K b. . 4i ・蚯 gWj :业••■: I •••亠十-I.F": -■■ _ 11 J ^1111 1111 111_屜可 环 山*1图8补偿后系统的bode图此时从图中可以看出，系统的相位裕度为 50.3度，幅值裕度足够大，能很好地满足系统的稳定性和快速响应性要求。
二、补偿后系统实时仿真1.补偿后时域内BUCK 变换器仿真图Dophyl2.补偿后时域内BUCK 动态波形图3U2S201510ODD3 002 anzB amt OQOT none 盯陌 oni图10补偿后时域内BUCK 动态波形图图10表明了系统的动态性能得到了改善，响应速度和稳态精度有很大程度 上的提高。
-0—— S-aq-JT □& 1499|Cont 叶 1＞单|打图9补偿后时域内BUCK 变换器仿真图CJ 0 [171 Qiim? Discret e, Ffi - EPlnst尺■士 曷jhial3.局部图选取0.0059s~0.0060s 时间内局部波形图进行分析。
a? 9.2? 9.岀 3.26 3.20 S3 ±32 朋 4 3.3E 536-3Tirr#on#i: 'Ui xlO图11局部图纹波大约为0.06V 左右，系统的稳态精度较好。
第五部分：总结本文通过对BUCK 变换器的建模与仿真，运用反馈补偿控制知识，最终完 成了一套控制补偿网络的设计，仿真结果也较好的验证了设计的正确性： 由开环 系统的响应时间长，稳态精度差，超调量过大等缺点，经过补偿环节的设计之后， 较好地解决了这些问题。
当然补偿设计也不是唯一的，设计过程中运用过了相关 经验公式，并简化了一些条件，最终形成的结果也肯定不是最佳的。
15.02 15 HJHh .J ■'・ J■ lib.:J .... 1..L.1 JT,111 ：-3屮・■ ■ T .I。
