土的本构模型综述

土的剑桥模型发展综述----97dbe56c-6ead-11ec-b680-7cb59b590d7d土体本构理论是岩土工程学科的重要基础理论。

随着对土体力学特性的不断深入,塑性理论逐渐被应用于土体本构关系的研究中来。

roscoe[1]于1963年提出著名的剑桥粘土模型,是应用塑性理论的代表,被看做现代土力学的开端。

在本构理论的研究和发展过程中，各种建模思想层出不穷，各种形式的土体本构模型层出不穷，但唯一公认的弹塑性模型是剑桥模型。

目前，国际岩土本构法的一个主要发展趋势是回归剑桥模型，并在剑桥模型的基础上对其进行改进和修正。

本文简要介绍了剑桥模式，并对剑桥模式的发展进行了系统评述。

1.关于剑桥模型及修正剑桥模型1958年至1963年，英国剑桥大学的Roscoe等人[1]在正常固结粘土和弱超固结粘土三轴试验的基础上，提出了剑桥粘土的本构模型，标志着人们对土壤力学性质的理解出现了第一次飞跃。

他们系统地将“帽”屈服准则、正交流动准则和加工硬化定律应用于cam模型，提出了临界状态线、状态边界界面和弹性壁等一系列物理概念，形成了第一个相对完整的土塑性模型。

Roscoc和Burland[2]进一步修正了剑桥模型，认为剑桥模型的屈服面轨迹应为椭圆，并给出了著名的修正剑桥模型。

可以说，剑桥模型开创了土壤力学的临界状态理论。

试验证明,对于正常固结粘土和弱固结的饱和重塑粘土,孔隙比e与外力p,q之间存在有唯一的关系,且不随应力路径而发生变化。

该模型本文试图描述在实验室试验中观察到的现象，即从初始状态加载到保持塑性恒定体积变形的临界状态。

其基本组成如下：(1)在(e,p)平面中,存在一条曲线,在正常固结粘性土中的所有应力遵循此路径,这被称为正常固结线(ncl)。

这条线提供了体积硬化规则,可以被广义化为一般应力条件。

（2）（E，P，q）空间中有一条直线，所有剩余态都遵循这条路径，这与实验类别和初始条件无关。

这条线平行于（E，P）平面上的正常固结线，在该平面上发生剪切变形而不发生体积变形。

文章编号（黑体加粗）：1000－7598－(2003) 02―0304―03（编号用Times New Roman）饱和土本构模型研究进展摘要：自20世纪50年代以来，随着计算机技术的发展，许多能够描述饱和土体复杂力学行为的本构模型相继被提出来，但由于模型数量较多，很多模型较为复杂，因此不被工程师们所接受。

综述近60年来饱和土体静力本构和动力本构的发展情况，对每种模型进行简单的介绍，以求尽可能多的囊括近年来较为成熟的各类模型，便于工程师与科研工作者对这些模型有所了解，并能在工程中进一步完善和应用。

关键词：中图分类号：TU 443（Times New Roman）文献标识码：AAdvance in research on constitutive model of saturated soilAbstract: s ince 1950’s, with the development of computer science, many constitutive models were proposed to describe the complicated nature of saturated soil. However, the number of the new model is too large and many of them are not accepted by engineers. We review the development of saturated soil constitutive and soil dynamics constitutive in nearly 60 years, and introduce as many relevant maturity models briefly as possibly in order to make engineers and scientists know about these models and utilize them in real projects.Key words:1.引言土作为一个自然形成的天然材料，具有复杂的物理力学性质，普遍认为用统一的土的本构模型完全模拟土的物理力学性质是十分困难的[1]，现有的模型普遍都具有局限性。

常用土体本构模型及其特点小结山中一草线弹性模型线弹性模型遵从虎克定律，只有2个参数，即弹性模量E和泊松比V,它是最简单的应力-应变关系，但无法描述土的很多特征，主要应用于早期的有限元分析及解析方法中，可用来近似模拟较硬的材料如岩土。

Duncan-Chang（ DC 模型DC模型是一种非线性弹性模型，它用双曲线来模拟土的三轴排水试验的应力-应变关系（图1）。

它侧重于刻画土体应力-应变曲线非线性的简单特征，通过弹性参数的调整来近似地考虑土体的塑性变形。

但所用的理论仍然是弹性理论而没有涉及到任何塑性理论，故仍不能反映如应力路径对变形的影响、土体的剪胀特性和球应力对剪应变的影响等土体的很多重要性质。

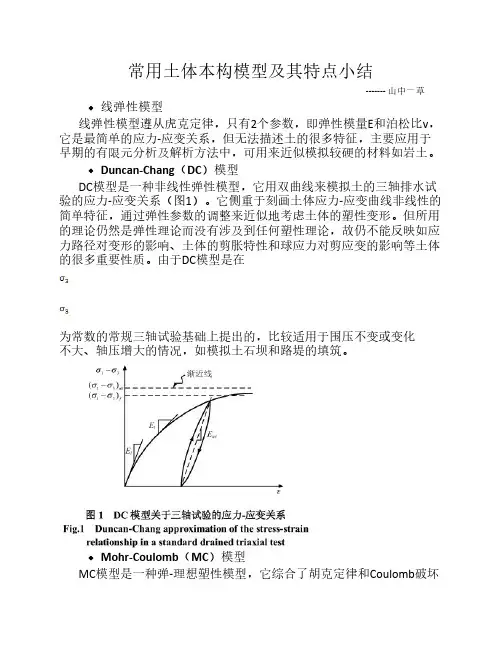
由于DC模型是在二为常数的常规三轴试验基础上提出的，比较适用于围压不变或变化不大、轴压增大的情况，如模拟土石坝和路堤的填筑。

图】IK模型关于三轴试验的应力-应变关系Fig.l Duncan-Chang approxiniathm of the siress-strainrd nt kinship Ln ft standard drained triAxt*! te&lMohr-Coulomb （MC）模型MC模型是一种弹-理想塑性模型，它综合了胡克定律和Coulomb破坏准则。

有5个参数，即控制弹性行为的2个参数：弹性模量E和泊松比v及控制塑性行为的3个参数：有效黏聚力c、有效内摩擦角和剪胀角。

MC模型采用了弹塑性理论，能较好地描述土体的破坏行为但却认为土体在达到抗剪强度之前的应力-应变关系符合胡克定律，因而并不能较好地描述土体在破坏之前的变形行为，且不能考虑应力历史的影响及区分加荷和卸荷。

故MC模型能较好地模拟土体的强度问题，MC模型的六凌锥形屈服面（图2）与土样真三轴试验的应力组合形成的屈服面吻合得较好，因此MC模型适合于低坝、边坡等稳定性问题的分析。

Drucker -Prager( DP)模型DP模型对MC模型的屈服面函数作了适当的修改，采用圆锥形屈服面（图3）来代替MC模型的六凌锥屈服面，易于程序的编制和进行数值计算。

常用土体本构模型及其特点小结------- 山中一草线弹性模型线弹性模型遵从虎克定律，只有2个参数，即弹性模量E和泊松比v，它是最简单的应力-应变关系，但无法描述土的很多特征，主要应用于早期的有限元分析及解析方法中，可用来近似模拟较硬的材料如岩土。

Duncan-Chang（DC）模型DC模型是一种非线性弹性模型，它用双曲线来模拟土的三轴排水试验的应力-应变关系（图1）。

它侧重于刻画土体应力-应变曲线非线性的简单特征，通过弹性参数的调整来近似地考虑土体的塑性变形。

但所用的理论仍然是弹性理论而没有涉及到任何塑性理论，故仍不能反映如应力路径对变形的影响、土体的剪胀特性和球应力对剪应变的影响等土体的很多重要性质。

由于DC模型是在为常数的常规三轴试验基础上提出的，比较适用于围压不变或变化不大、轴压增大的情况，如模拟土石坝和路堤的填筑。

Mohr-Coulomb（MC）模型MC模型是一种弹-理想塑性模型，它综合了胡克定律和Coulomb破坏准则。

有5个参数，即控制弹性行为的2个参数：弹性模量E和泊松比v及控制塑性行为的3个参数：有效黏聚力c、有效内摩擦角和剪胀角。

MC模型采用了弹塑性理论，能较好地描述土体的破坏行为但却认为土体在达到抗剪强度之前的应力-应变关系符合胡克定律，因而并不能较好地描述土体在破坏之前的变形行为，且不能考虑应力历史的影响及区分加荷和卸荷。

故MC模型能较好地模拟土体的强度问题，MC模型的六凌锥形屈服面（图2）与土样真三轴试验的应力组合形成的屈服面吻合得较好，因此MC模型适合于低坝、边坡等稳定性问题的分析。

Drucker -Prager（DP）模型DP模型对MC模型的屈服面函数作了适当的修改，采用圆锥形屈服面（图3）来代替MC模型的六凌锥屈服面，易于程序的编制和进行数值计算。

它存在与MC模型同样地缺点，相对而言，在模拟岩土材料时，MC 模型较DP模型更加适合。

修正剑桥模型（MCC）MCC模型为等向硬化的弹塑性模型，它修正了剑桥模型的弹头形屈服面，采用帽子屈服面（椭圆形）（图4），以塑性体应变为硬化参数，能较好地描述黏性土在破坏之前的非线性和依赖于应力水平或应力路径的变形行为，MCC模型从理论上和试验上都较好地阐明了土体的弹塑性变形特征，是应用最为广泛的软土本构模型之一。

土的本构关系土体是天然地质材料的历史产物。

土是一种复杂的多孔材料,在受到外界荷载作用后,其变形具有以下特性：①土体的变形具有明显的非线性,如:土体的压缩试验e～p 曲线、三轴剪切试验的应力—应变关系曲线、现场承载板试验所得的p～s曲线等; ②土体在剪切应力作用下会产生塑性应变,同时球应力也引起塑性应变; ③土体尤其是软粘土,具有十分明显的流变特性;④由于土体的构造或沉积等原因,使土具有各向异性; ⑤紧砂、超固结粘土等在受剪后都表现出应变软化的特性; ⑥土体的变形与应力路径有关,证明不同的加载路径会出现较大的差别; ⑦剪胀性等。

为了更好地描述土体的真实力学—变形特性,建立其应力、应变和时间的关系,在各种试验和工程实践经验的基础上提出一种数学模型,即: 土体的本构关系。

自从Roscoe等人首次建立了剑桥模型以来, 土的本构关系的研究经历了一个蓬勃发展的阶段, 出现了一些具有实用价值的本构模型。

虽然很多的理论为建立土的本构关系提供了有力的工具, 但是由于土是一种三相体材料, 在性质上既不同于固体也不同于液体, 是介于两者之间的特殊材料, 所以人们常借助于固体力学或流体力学理论, 同时结合工程实践经验来解决土工问题, 从而研究土的本构关系形成了自己一套独特的方法—半理论半经验的方法。

建立一个成功的本构关系关键有两点：第一要建立一个函数能较好地反映土在受力下的响应特征；第二要充分利用试验结果提供的数据比较容易地确定模型参数。

模型都需要满足以下基本条件：（1）不违背更高一级的基本物理原理（如热力学第一、第二定律）。

（2）建立在一定的力学理论基础之上（如弹性理论、塑性理论等）。

（3）模型参数能够通过常规试验求取。

从工程应用的角度出发，研究问题的精度就需要进行合理的控制，从而在计算精度与计算设备、计算难度、计算时间以及计算成本之间获得平衡。

另外，任何理论、方法都应以实践应用为目的，这样才具有价值。

综合上述两点，从工程应用的角度去分析各种土的本构关系是非常有必要的。

正常固结黏土的三维弹塑性本构模型正常固结黏土的三维弹塑性本构模型正常固结黏土是地下工程中常见的基础土。

由于它的重要性，建立一个准确的三维弹塑性本构模型对于分析土体变形和破裂行为至关重要。

正常固结黏土的三维弹塑性本构模型被广泛研究，本文将介绍几种常见的模型及其特点。

虽然弹性理论和弹塑性理论可以用来描述正常固结黏土的变形行为，但由于正常固结黏土实际上是一种非线性材料，因此需要使用弹塑性本构模型来更好地模拟实际情况。

1. 经典Drucker-Prager本构模型经典Drucker-Prager本构模型是最早的正常固结黏土三维弹塑性本构模型之一。

该模型假设土体处于剪切强度线上方，并在下垫面施加一定的正应力。

该模型的主要局限在于它是刚性塑性的，无法模拟正常固结黏土的压缩行为。

其次，该模型只能描述单一的剪切带，难以应用于非均质土体的模拟。

2. Mohr-Coulomb本构模型Mohr-Coulomb本构模型是较为常用的正常固结黏土三维弹塑性本构模型之一。

基于Mohr-Coulomb准则，该模型考虑到了土体的体积塑性，并可以通过改变剪切强度线来模拟不同类型的土。

该模型的缺点在于它无法模拟土体的非线性压缩行为。

此外，该模型也难以应用于非均质土体的模拟。

3. 双重Drucker-Prager本构模型双重Drucker-Prager本构模型是在经典Drucker-Prager本构模型的基础上进行改进的。

其允许土体出现多个剪切带，同时可以对非线性压缩行为进行较好的模拟。

该模型的缺点在于它仅适用于单一的土体类型模拟，并不能很好地模拟不同类型的土。

4. Cam-clay模型Cam-clay模型假设土体是一种可压缩的材料，并且它的体积变化与剪切应变有关。

该模型可以很好地模拟土体的体积塑性行为。

该模型的缺点在于它无法模拟土体的弹性行为，因此只适用于较大的应变范围内。

此外，该模型也难以应用于非均质土体解析。

总体来说，正常固结黏土的三维弹塑性本构模型具有复杂性和多样性。

岩土本构模型原理及应用简述 摘要：简述了岩土本构模型中弹性本构模型、弹塑性本构模型及粘弹塑性模型的建立、应用范围和局限性。认为当前的岩土本构模型，简单便于计算的模型不能反映岩土真实的力学性状，而精细复杂的模型参数难以确定，难以推广应用。直至现阶段还没有一种能适应任何条件的普遍本构模型，目前岩土本构模型研究有必要向这方面发展。

关键词：岩土弹性本构模型 弹塑性本构模型 粘弹塑本构模型 在实际工程中岩土体常常有很复杂的应力-应变特性，如非线性、弹性、塑性、粘性以及剪胀性、应变硬化（软化）、各向异性等，同时受到应力路径、应力历史以及岩土的状态、组成、结构和温度不同程度的影响。因此为了反映岩土真实的力学性状，必须建立较为复杂的本构模型。而实际工程应用中，在满足一定的精度条件下，又要求简单实用。虽然至今的岩土本构模型达数百种，但大体上分为下述几类：弹性模型、弹塑性模型、粘弹塑性模型等。

1 弹性本构模型 弹性模型是建立在弹性理论基础上的本构模型。最简单的是线弹性模型，即广义胡克定律。非线性弹性模型一般可分为三类：Cauchy弹性模型、超弹模型和次弹性模型。非线性弹性模型是线弹性模型的推广，按照拟合应力-应变曲线的形状分为：折线型、双曲线型、对数曲线型等。按照采用的弹性系数又可分为E-μ（弹性模量-泊松比）非线性弹性模型，K-G（体积变形模量-切变模量）非线性弹性模型，以及用其他形式表示的弹性模型。

1.1 线弹性本构模型 弹性是一种理想的固体特性。实际土体在外载荷作用下，只有在应变很小时才发生弹性变形。模拟土体应力应变性质的最古老、最简单的方法是采用线弹性模型，即假设土体应力一应变之间存在一一对应的线形关系：σij=F（εij），反映在土体应力一应变关系矩阵式{σ}=[D]{ε}中，弹性模量矩阵[D]是常量。

由于土体弹性性质的方向性决定了各线弹性模型独立弹性常数个数。对一般的均质连续各向异性弹性体，有21个独立弹性常数，正交各向异性线弹性模型具有9个独立弹性常数，横观各向同性线弹性模型具有5个独立弹性常数，最简单的各向同性线弹性模型（虎克定律）具有2个独立弹性常数。

常用土体本构模型及其特点小结-------山中一草线弹性模型线弹性模型遵守虎克定律，只有2个参数，即为弹性模量e和泊松比v，它就是最简单的形变-快速反应关系，但无法叙述土的很多特征，主要应用于早期的有限元分析及解析方法中，需用去对数演示较软的材料例如岩土。

?duncan-chang（dc）模型dc模型是一种非线性弹性模型，它用双曲线来模拟土的三轴排水试验的应力-应变关系（图1）。

它侧重于刻画土体应力-应变曲线非线性的简单特征，通过弹性参数的调整来近似地考虑土体的塑性变形。

但所用的理论仍然是弹性理论而没有涉及到任何塑性理论，故仍不能反映如应力路径对变形的影响、土体的剪胀特性和球应力对剪应变的影响等土体的很多重要性质。

由于dc模型是在为常数的常规三轴试验基础上提出的，比较适用于围压不变或变化不大、轴压增大的情况，如模拟土石坝和路堤的填筑。

mohr-coulomb（mc）模型mc模型是一种弹-理想塑性模型，它综合了胡克定律和coulomb破坏准则。

有5个参数，即控制弹性行为的2个参数：弹性模量e和泊松比v及控制塑性行为的3个参数：有效黏聚力c、有效内摩擦角和剪胀角。

mc模型采用了弹塑性理论，能较好地描述土体的破坏行为但却认为土体在达到抗剪强度之前的应力-应变关系符合胡克定律，因而并不能较好地描述土体在破坏之前的变形行为，且不能考虑应力历史的影响及区分加荷和卸荷。

故mc模型能较好地模拟土体的强度问题，mc模型的六凌锥形屈服面（图2）与土样真三轴试验的应力组合形成的屈服面吻合得较好，因此mc模型适合于低坝、边坡等稳定性问题的分析。

drucker-prager（dp）模型dp模型对mc模型的屈服面函数作了适当的修改，采用圆锥形屈服面（图3）来代替mc模型的六凌锥屈服面，易于程序的编制和进行数值计算。

它存在与mc模型同样地缺点，相对而言，在模拟岩土材料时，mc模型较dp模型更加适合。

修正剑桥模型（mcc）mcc模型为等向硬化的弹塑性模型，它修正了剑桥模型的弹头形屈服面，采用帽子屈服面（椭圆形）（图4），以塑性体应变为硬化参数，能较好地描述黏性土在破坏之前的非线性和依赖于应力水平或应力路径的变形行为，mcc模型从理论上和试验上都较好地阐明了土体的弹塑性变形特征，是应用最为广泛的软土本构模型之一。

饱和黄土动力本构模型及其在桩—土—结构体系地震动力相互作用中的应用饱和黄土动力本构模型及其在桩—土—结构体系地震动力相互作用中的应用地震对于建筑结构的影响是一个长期以来备受关注的问题。

特别是当建筑结构位于饱和黄土地区时，地震作用下桩—土—结构体系的相互作用将更为复杂。

因此，研究饱和黄土的动力本构模型以及其在地震动力相互作用中的应用是非常重要的。

首先，我们需要了解什么是饱和黄土。

饱和黄土是一种具有特殊土性质的土壤，其主要成分是粘粒和胶体颗粒。

它具有较高的含水量和较强的液态状态，因此在地震中容易发生液化现象。

液化是指土壤在地震作用下失去强度，表现出类似液体的特性。

这就给建筑结构的稳定性和安全性带来了较大的挑战。

在研究饱和黄土的动力本构模型时，我们需要考虑一系列因素，包括土壤的基本性质、动力特性、孔隙水压力以及土体的非线性行为等。

在地震中，土壤的动力特性是非常重要的，它包括土体的固有周期、阻尼特性以及动力刚度等。

固有周期是指土体在地震作用下振动的周期，可以用来评估土体的稳定性。

阻尼特性则是指土体消耗能量的能力，对减小地震作用对建筑结构的影响至关重要。

在考虑土体的非线性行为时，我们需要将土体看作一个复杂的弹塑性体。

在地震动力下，饱和黄土的应变—应力关系呈现出非线性特点，包括弹性阶段、塑性阶段以及液化阶段等。

了解这些非线性特点可以帮助我们更好地预测地震对建筑结构的影响，并提出有效的改善措施。

在地震动力相互作用中，桩—土—结构体系也发挥着重要的作用。

桩和土体之间的相互作用可以通过简化的数值模型来表示，但在实际工程中，需要从更细致的角度考虑各种因素。

例如，土壤的液化将导致桩的承载力减小，从而影响结构的稳定性。

因此，我们需要建立更精确的模型来描述桩—土—结构体系的相互作用，并通过合理的设计来抵抗地震的影响。

近年来，随着地震工程的发展，研究者们提出了一些新的方法和技术来解决饱和黄土动力本构模型及其在桩—土—结构体系地震动力相互作用中的问题。

混凝土本构模型综述### 学号：#############摘要：木文综述了近年来国内外混凝土木构模型的一些讨论状况.对国内外最新的几种混凝上木构模型进行了述评.指出了各种模型的适用条件及其优缺点.最终.依据现有的讨论成果及混凝上材料的试验讨论结果，得出了建立混凝上动力本构模型中应考虑的主要因素，并且从几个方面展望混凝土本构模型的进展方向。

关键字：混凝土；本构模型；经典力学基础；新兴力学基础引言凝土是以水泥为胶凝材料的多组分多相非匀质的复合材料，对混凝土强度的形成、破损的过程与机理以及如何设计和计算强度，都是特别简单的问题。

混凝土的本构模型是指描述材料力学性质的数学表达式即对材料的应力应变性状的数学模拟.迄今为止人们对各种材料提出的各种各样的本构模型数不胜数依据这些模型对材料力学性能特征的描述可归纳为四大类：1线弹性模型2非线弹性模型3塑性理论模型4其它力学理论模型.线弹性模型和塑性理论模型以成熟的力学理论（弹性理论和塑性理论）的观点和方法为基础移植于特定材料而建立.非线弹性模型以线弹性模型为基础是弹性理论中广义虎克定律的推广主要依据材料的试验数据和规律进行总结和回归分析而得到.其它力学理论模型是指借鉴一些新兴的力学分支结合特定材料特点推导而得的相应本构模型.⑴ 1基于经典力学基础上的本构模型⑵⑶ 1.1线弹性本构模型该模型假定混凝土为抱负弹性体应力与应变成正比应变在加卸载时沿同始终线变化完全卸载后无残余变形应力与应变有确定的唯一关系弹性模量为常量.考虑混凝土材料性能的方向性差异尚可建立不同简单程度的线弹性本构模型如各向异性本构模型正交异性本构模型各向同性本构模型等⑷。

这类模型适用于：①混凝土的应力水平较低内部微裂缝和塑性变形很小②预应力结构或受约束结构开裂之前③体形简单结构的初步分析或近似计算④某些结构选用不同的本构模型对其计算结果不敏感时等状况.⑸该模型是迄今进展最成熟的材料本构模型，能较好地描述混凝土受拉和低应力受压时的性能，也适于描述混疑土其它受力状况下的初始阶段，基于这类模型运用到有限元分析中已有很多胜利的例子。