二、八、十、十六进制对照表
- 格式:pptx
- 大小:64.52 KB
- 文档页数:1
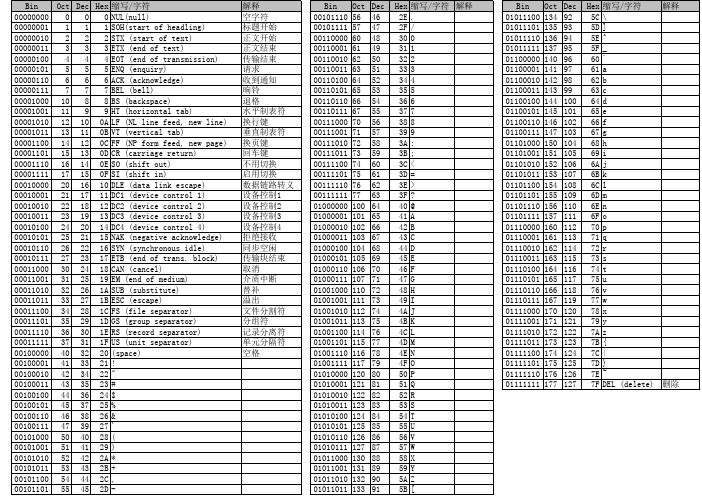
Bin Oct Dec Hex缩写/字符解释Bin Oct Dec Hex缩写/字符解释Bin Oct Dec Hex缩写/字符解释00000000000NUL(null)空字符 0010111056462E.01011100134925C\00000001111SOH(start of headling)标题开始0010111157472F/ 01011101135935D]00000010222STX (start of text)正文开始00110000604830001011110136945E^00000011333ETX (end of text)正文结束00110001614931101011111137955F_00000100444EOT (end of transmission)传输结束001100106250322011000001409660`00000101555ENQ (enquiry)请求001100116351333011000011419761a00000110666ACK (acknowledge)收到通知001101006452344011000101429862b00000111777BEL (bell)响铃001101016553355011000111439963c000010001088BS (backspace)退格0011011066543660110010014410064d000010011199HT (horizontal tab)水平制表符0011011167553770110010114510165e 0000101012100A LF (NL line feed, new line)换行键0011100070563880110011014610266f0000101113110B VT (vertical tab)垂直制表符 0011100171573990110011114710367g 0000110014120C FF (NP form feed, new page)换页键0011101072583A: 0110100015010468h0000110115130D CR (carriage return) 回车键0011101173593B;0110100115110569i 0000111016140E SO (shift out)不用切换0011110074603C< 011010101521066A j0000111117150F SI (shift in)启用切换0011110175613D=011010111531076B k 00010000201610DLE (data link escape) 数据链路转义0011111076623E> 011011001541086C l 00010001211711DC1 (device control 1) 设备控制10011111177633F?011011011551096D m 00010010221812DC2 (device control 2)设备控制2010000001006440@ 011011101561106E n 00010011231913DC3 (device control 3) 设备控制3010000011016541A011011111571116F o 00010100242014DC4 (device control 4)设备控制4 010000101026642B 0111000016011270p 00010101252115NAK (negative acknowledge) 拒绝接收 010000111036743C0111000116111371q 00010110262216SYN (synchronous idle) 同步空闲010001001046844D 0111001016211472r 00010111272317ETB (end of trans. block)传输块结束 010001011056945E0111001116311573s 00011000302418CAN (cancel) 取消 010001101067046F0111010016411674t 00011001312519EM (end of medium)介质中断 010001111077147G0111010116511775u0001101032261A SUB (substitute)替补010010001107248H 0111011016611876v0001101133271B ESC (escape) 溢出010010011117349I0111011116711977w 0001110034281C FS (file separator) 文件分割符01001010112744A J 0111100017012078x0001110135291D GS (group separator) 分组符01001011113754B K0111100117112179y 0001111036301E RS (record separator) 记录分离符01001100114764C L 011110101721227A z0001111137311F US (unit separator)单元分隔符01001101115774D M011110111731237B{ 00100000403220(space)空格 01001110116784E N 011111001741247C| 00100001413321!01001111117794F O011111011751257D} 00100010423422"010100001208050P 011111101761267E~ 00100011433523#010100011218151Q011111111771277F DEL (delete)删除00100100443624$010100101228252R00100101453725%010100111238353S00100110463826&010101001248454T00100111473927'010101011258555U00101000504028(010101101268656V00101001514129)010101111278757W0010101052422A*010110001308858X0010101153432B+010110011318959Y0010110054442C,01011010132905A Z0010110155452D-01011011133915B[。


一.16进制代码查询对照表
16进制:用16作为基数的计数系统。
用数字0-9和字母a-f(或其大写A-F)表示0到15。
用H表示十六进制
扩展资料:
16进制:用16作为基数的计数系统。
用数字0-9和字母a-f(或其大写A-F)表示0到15。
用H表示十六进制
十六进制数转换成十进制数
2进制,用两个阿拉伯数字:0、1;
8进制,用八个阿拉伯数字:0、1、2、3、4、5、6、7;
10进制,用十个阿拉伯数字:0到9;
16进制,用十六个阿拉伯数字……等等,印度人只发明了10个数字啊?
16进制就是逢16进1,但我们只有0~9这十个数字,所以我们用A,B,C,D,E,F这六个字母来分别表示10,11,12,13,14,15。
字母不区分大小写。
十六进制数的第0位的权值为16的0次方,第1位的权值为16的1次方,第2位的权值为16的2次方……
所以,在第N(N从0开始)位上,如果是是数X (X 大于等于0,并且X小于等于15,即:F)表示的大小为X * 16的N次方。

16进制对照表是什么?
用H表示十六进制
扩展资料:
16进制:用16作为基数的计数系统。
用数字0-9和字母a-f(或其大写A-F)表示0到15。
用H表示十六进制
十六进制数转换成十进制数
2进制,用两个阿拉伯数字:0、1;
8进制,用八个阿拉伯数字:0、1、2、3、4、5、6、7;
10进制,用十个阿拉伯数字:0到9;
16进制,用十六个阿拉伯数字……等等,印度人只发明了10个数字啊?
16进制就是逢16进1,但我们只有0~9这十个数字,所以我们用A,B,C,D,E,F这六个字母来分别表示10,11,12,13,14,15。
字母不区分大小写。
十六进制数的第0位的权值为16的0次方,第1位的权值为16的1次方,第2位的权值为16的2次方……
所以,在第N(N从0开始)位上,如果是是数X (X 大于等于0,并且X小于等于15,即:F)表示的大小为X * 16的N次方。
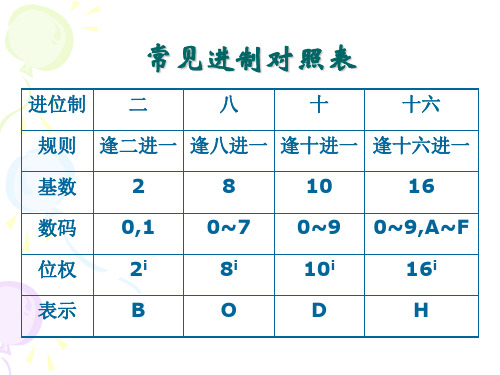

进制转换对照表(0~255) - 十进制,十六进制,八进制,二进制Dec Hex Oct Bin0 1 2 3 4 5 6 7 8 9101112131415 0123456789ABCDEF00000100200300400500600701001101201301401501601700000000000000010000001000000011000001000000010100000110000001110000100000001001000010100000101100001100000011010000111000001111Dec Hex Oct Bin16171819202122232425262728293031101112131415161718191A1B1C1D1E1F02002102202302402502602703003103203303403503603700010000000100010001001000010011000101000001010100010110000101110001100000011001000110100001101100011100000111010001111000011111Dec Hex Oct Bin32333435363738394041424344454647202122232425262728292A2B2C2D2E2F04004104204304404504604705005105205305405505605700100000001000010010001000100011001001000010010100100110001001110010100000101001001010100010101100101100001011010010111000101111Dec Hex Oct Bin48495051525354555657585960616263303132333435363738393A3B3C3D3E3F06006106206306406506606707007107207307407507607700110000001100010011001000110011001101000011010100110110001101110011100000111001001110100011101100111100001111010011111000111111Dec Hex Oct Bin64656667686970 4041424344454610010110210310410510601000000010000010100001001000011010001000100010101000110Dec Hex Oct Bin808182838485865051525354555612012112212312412512601010000010100010101001001010011010101000101010101010110Dec Hex Oct Bin969798991001011026061626364656614014114214314414514601100000011000010110001001100011011001000110010101100110Dec Hex Oct Bin1121131141151161171187071727374757616016116216316416516601110000011100010111001001110011011101000111010101110110717273747576777879 4748494A4B4C4D4E4F1071101111121131141151161170100011101001000010010010100101001001011010011000100110101001110010011118788899091929394955758595A5B5C5D5E5F1271301311321331341351361370101011101011000010110010101101001011011010111000101110101011110010111111031041051061071081091101116768696A6B6C6D6E6F1471501511521531541551561570110011101101000011010010110101001101011011011000110110101101110011011111191201211221231241251261277778797A7B7C7D7E7F167170171172173174175176177011101110111100001111001011110100111101101111100011111010111111001111111Dec Hex Oct Bin128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 808182838485868788898A8B8C8D8E8F20020120220320420520620721021121221321421521621710000000100000011000001010000011100001001000010110000110100001111000100010001001100010101000101110001100100011011000111010001111Dec Hex Oct Bin144145146147148149150151152153154155156157158159909192939495969798999A9B9C9D9E9F22022122222322422522622723023123223323423523623710010000100100011001001010010011100101001001010110010110100101111001100010011001100110101001101110011100100111011001111010011111Dec Hex Oct Bin160161162163164165166167168169170171172173174175A0A1A2A3A4A5A6A7A8A9AAABACADAEAF24024124224324424524624725025125225325425525625710100000101000011010001010100011101001001010010110100110101001111010100010101001101010101010101110101100101011011010111010101111Dec Hex Oct Bin176177178179180181182183184185186187188189190191B0B1B2B3B4B5B6B7B8B9BABBBCBDBEBF26026126226326426526626727027127227327427527627710110000101100011011001010110011101101001011010110110110101101111011100010111001101110101011101110111100101111011011111010111111Dec Hex Oct Bin Dec Hex Oct Bin Dec Hex Oct Bin Dec Hex Oct Bin192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 C0C1C2C3C4C5C6C7C8C9CACBCCCDCECF30030130230330430530630731031131231331431531631711000000110000011100001011000011110001001100010111000110110001111100100011001001110010101100101111001100110011011100111011001111208209210211212213214215216217218219220221222223D0D1D2D3D4D5D6D7D8D9DADBDCDDDEDF32032132232332432532632733033133233333433533633711010000110100011101001011010011110101001101010111010110110101111101100011011001110110101101101111011100110111011101111011011111224225226227228229230231232233234235236237238239E0E1E2E3E4E5E6E7E8E9EAEBECEDEEEF34034134234334434534634735035135235335435535635711100000111000011110001011100011111001001110010111100110111001111110100011101001111010101110101111101100111011011110111011101111240241242243244245246247248249250251252253254255F0F1F2F3F4F5F6F7F8F9FAFBFCFDFEFF36036136236336436536636737037137237337437537637711110000111100011111001011110011111101001111010111110110111101111111100011111001111110101111101111111100111111011111111011111111一:简述:进位计数制:是人们利用符号来计数的方法。
进制转换对照表(0~255) - 十进制,十六进制,八进制,二进制一:简述:进位计数制:是人们利用符号来计数的方法。
一种进位计数制包含一组数码符号和两个基本因素。
(1)数码:用不同的数字符号来表示一种数制的数值,这些数字符号称为”数码”。
(2)基:数制所使用的数码个数称为”基”。
(3)权:某数制每一位所具有的值称为”权”。
二:进制转换的理论1、二进制数、十六进制数转换为十进制数:用按权展开法把一个任意R进制数a n a n-1 ...a1a0 . a-1 a-2...a-m转换成十进制数,其十进制数值为每一位数字与其位权之积的和。
a n×R n + a n-1×R n-1 +…+ a1×R 1 + a0×R 0 + a-1×R-1+ a-2×R-2+ …+ a-m ×R-m2:十进制转化成R进制十进制数轮换成R进制数要分两个部分:整数部分:除R取余数,直到商为0,得到的余数即为二进数各位的数码,余数从右到左排列(反序排列)。
小数部分:乘R取整数,得到的整数即为二进数各位的数码,整数从左到右排列(顺序排列)。
3:十六进制转化成二进制每一位十六进制数对应二进制的四位,逐位展开。
4:二进制转化成十六进制将二进制数从小数点开始分别向左(对二进制整数)或向右(对二进制小数)每四位组成一组,不足四位补零。
三:具体实现1:二进制转换成十进制任何一个二进制数的值都用它的按位权展开式表示。
例如:将二进制数(10101.11)2转换成十进制数。
(10101.11)2=1*24+0*23+1*22+0*21+1*20+1*2-1+1*2-2=24+22+20+2-1+2-2=(21.75)102:十进制整理转换成二进制将十进制整数转换成二进制整数采用“除2取倒余法”。
即将十进制整数除以2,得到一个商和一个余数;再将商除以2,又得到一个商和一个余数;以此类推,直到商等于零为止。