流体力学 第三章 流体运动学与动力学基础
- 格式:doc
- 大小:509.50 KB
- 文档页数:40



第三章 流体运动学基础§3—1研究流体流动的方法一、基本概念场-设在空间的某个区域内定义了标量函数或矢量函数,则称定义了相应函数的空间区域为场。
如果研究的是标量函数则称此场为标量场;如果研究的是矢量函数,则称之为矢量场;如果同一时刻场内各点函数的值都相等,则称此场为均匀场,反之为不均匀场,如果场内函数不依于时间,即不随时间改变,则称此场为定常场,反之称为不定常场。
场的分类如下:⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧密度场压力场标量场力场速度场矢量场 流场―充满运动流体的场称为流场。
二、研究流体运动的欧拉法欧拉法―欧拉法是通过下列两个方面来描述整个流场情况的:(1)在空间固定点上流体的各种物理量(如速度、压力)随时间的变化。
(2)在相邻的空间点上这些物理量的变化 1、速度表示法欧拉法是以流场中每一空间位置作为描述对象,描述在这些位置上流体的物理参数随时间的变化。
显然,同一时刻,流体内部各空间点上流体质点的速度可以是不同的,即V是(x, y, z )的函数。
同一空间点上,不同时刻,流体质点的速度也是不同的。
即V又是t 的函数。
另一方面x , y , z 又可以看作是流体质点的坐标,而流体质点的坐标又是时间的函数。
因此: x = x ( t ) y = y ( t ) z = z ( t )),,,(),,,(),,,(t z y x w w t z y x t z y x u u ===υυ故:V =V(x , y , z, t )同理:),,,(t z y x p p =),,,(t z y x ρρ=2、流体质点的加速度流体质点的加速度为:tVa d d =则:z u w y u x u u t u t z z u t y y u t x x u t u t u a x ∂∂+∂∂+∂∂+∂∂=∂∂⋅∂∂+∂∂⋅∂∂+∂∂⋅∂∂+∂∂==υd d z w y x u t t a y ∂∂+∂∂+∂∂+∂∂==υυυυυυd d zw w y w x w u t w t w a z ∂∂+∂∂+∂∂+∂∂==υd d 用矢量表示为: V V tVt V a)(d d ∇⋅+∂∂==其中yk y j x i ∂∂+∂∂+∂∂=∇ 为哈密顿算式。


第三章流体运动学与动力学基础主要内容基本概念欧拉运动微分方程连续性方程——质量守恒*伯努利方程——能量守恒** 重点动量方程——动量守恒** 难点方程的应用第一节研究流体运动的两种方法流体质点:物理点。
是构成连续介质的流体的基本单位,宏观上无穷小(体积非常微小,其几何尺寸可忽略),微观上无穷大(包含许许多多的流体分子,体现了许多流体分子的统计学特性)。
空间点:几何点,表示空间位置。
流体质点是流体的组成部分,在运动时,一个质点在某一瞬时占据一定的空间点(x,y,z)上,具有一定的速度、压力、密度、温度等标志其状态的运动参数。
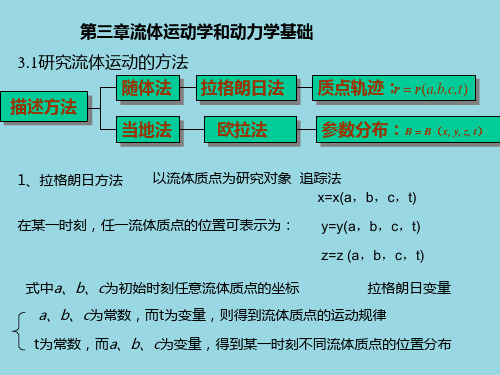
拉格朗日法以流体质点为研究对象,而欧拉法以空间点为研究对象。
一、拉格朗日法(跟踪法、质点法)Lagrangian method1、定义:以运动着的流体质点为研究对象,跟踪观察个别流体质点在不同时间其位置、流速和压力的变化规律,然后把足够的流体质点综合起来获得整个流场的运动规律。
2、拉格朗日变数:取t=t0时,以每个质点的空间坐标位置为(a,b,c)作为区别该质点的标识,称为拉格朗日变数。
3、方程:设任意时刻t,质点坐标为(x,y,z) ,则:x = x(a,b,c,t)y = y(a,b,c,t) z = z(a,b,c,t) 4、适用情况:流体的振动和波动问题。
5、优点: 可以描述各个质点在不同时间参量变化,研究流体运动轨迹上各流动参量的变化。
缺点:不便于研究整个流场的特性。
二、欧拉法(站岗法、流场法)Eulerian method1、定义:以流场内的空间点为研究对象,研究质点经过空间点时运动参数随时间的变化规律,把足够多的空间点综合起来得出整个流场的运动规律。
2、欧拉变数:空间坐标(x ,y ,z )称为欧拉变数。
3、方程:因为欧拉法是描写流场内不同位置的质点的流动参量随时间的变化,则流动参量应是空间坐标和时间的函数。
位置: x = x(x,y,z,t)y = y(x,y,z,t) z = z(x,y,z,t)速度: u x =u x (x,y,z,t )u y =u y (x,y,z,t ) u z =u z (x,y,z,t )同理: p =p (x,y,z,t ) ,ρ=ρ(x,y,z,t) 说明: x 、y 、z 也是时间t 的函数。
李玉柱流体力学课后题答案第三章第三章流体运动学3-1 已知某流体质点做匀速直线运动,开始时刻位于点A(3,2,1),经过10秒钟后运动到点B(4,4,4)。
试求该流体质点的轨迹方程。
tt3t解:3-2 已知流体质点的轨迹方程为试求点A(10,11,3)处的加速度α值。
解:由10,解得15.2把代入上式得-3 已知不可压缩流体平面流动的流速场为,其中,流速、位置坐标和时间单位分别为m/s、m和s。
求当t,l s时点A(1,2)处液体质点的加速度。
解:根据加速度的定义可知:当t,l s时点A(1,2) 处液体质点的加速度为:于是,加速度a加速度a与水平方向(即x方向)的夹角: 的大小:-4 已知不可压缩流体平面流动的流速分量为。
求(1) t,0时,过(0,0)点的迹线方程;(2) t,1时,过(0,0)点的流线方程。
解:(1) 将带入迹线微分方程dt得 uvt2解这个微分方程得迹线的参数方程:将时刻,点(0,0)代入可得积分常数:。
将代入得:t3所以:,将时刻,点(0,0)代入可得积分常数:。
6 联立方程,消去得迹线方程为:(2) 将带入流线微分方程dxdy得y2t被看成常数,则积分上式得,c=0 2y2时过(0,0)点的流线为3-5 试证明下列不可压缩均质流体运动中,哪些满足连续性方程,哪些不满足连续性方程(连续性方程的极坐标形式可参考题3—7)。
解:对于不可压缩均质流体,不可压缩流体的连续方程为。
直角坐标系中不可压缩流体的连续性方程为:。
,因,满足,因,满足,因,满足,满足,因,满足,因,满足,因在圆柱坐标系中不可压缩流体的连续性方程为:。
,满足,因,满足,因,不满足,因,仅在y=0处满足,因其中,k、α和C均为常数,式(7)和(8)中3-6 已知圆管过流断面上的流速分布为,umax为管轴处最大流速,r0为圆管半径,r为某点到管轴的距离。
试求断面平均流速V与umax之间的关系。
2解:断面平均速度Ar0Ar02r04r3r024r0umax3-7 利用图中所示微元体证明不可压缩流体平面流动的连续性微分方程的极坐标形式为解:取扇形微元六面体,体积,中心点M密度为,速度为,r向的净出质量dmr 为类似有若流出质量,控制体内的质量减少量dmV可表示为。
封面作者:Pan Hongliang仅供个人学习第一章流体及其主要物理性质1-1.轻柴油在温度15ºC时相对密度为0.83,求它的密度和重度。
解:4ºC时相对密度:所以,1-2.甘油在温度0ºC时密度为1.26g/cm3,求以国际单位表示的密度和重度。
解:1-3.水的体积弹性系数为1.96×109N/m2,问压强改变多少时,它的体积相对压缩1%?解:1-4.容积4m3的水,温度不变,当压强增加105N/m2时容积减少1000cm3,求该水的体积压缩系数βp和体积弹性系数E。
解:1-5.用200L汽油桶装相对密度为0.70的汽油,罐装时液面上压强为1个大气压,封闭后由于温度变化升高了20ºC,此时汽油的蒸气压为0.18大气压。
若汽油的膨胀系数为0.0006ºC-1,弹性系数为14000kg/cm2。
试计算由于压力及温度变化所增减的体积?问灌桶时每桶最多不超过多少公斤为宜?解:E=E’·g=14000×9.8×104PaΔp=0.18at所以,从初始状态积分到最终状态得:另解:设灌桶时每桶最多不超过V升,则(1大气压=1Kg/cm2)V=197.6升dV t=2.41升dV p=2.52×10-3升G=0.1976×700=138Kg=1352.4N1-6.石油相对密度0.9,粘度28cP,求运动粘度为多少m2/s?解:1-7.相对密度0.89的石油,温度20ºC时的运动粘度为40cSt,求动力粘度为多少?解:ν=40cSt=0.4St=0.4×10-4m2/sμ=νρ=0.4×10-4×890=3.56×10-2 Pa·s1-8.图示一平板在油面上作水平运动,已知运动速度u=1m/s,板与固定边界的距离δ=1,油的动力粘度μ=1.147Pa·s,由平板所带动的油层的运动速度呈直线分布,求作用在平板单位面积上的粘性阻力为多少?解:1-9.如图所示活塞油缸,其直径D=12cm,活塞直径d=11.96cm,活塞长度L=14cm,油的μ=0.65P,当活塞移动速度为0.5m/s时,试求拉回活塞所需的力F=?解:A=πdL , μ=0.65P=0.065 Pa·s , Δu=0.5m/s , Δy=(D-d)/2第二章流体静力学2-1. 如图所示的U形管中装有水银与水,试求:(1)A、C两点的绝对压力及表压各为多少?(2)A、B两点的高度差为多少?解:①p A表=γh水=0.3mH2O=0.03at=0.3×9800Pa=2940Pap A绝=p a+ p A表=(10+0.3)mH2O=1.03at=10.3×9800Pa=100940Pap C表=γhg h hg+ p A表=0.1×13.6m H2O+0.3mH2O=1.66mH2O=0.166at=1.66×9800Pa=16268Pap C绝=p a+ p C表=(10+1.66)mH2O=11.66 mH2O=1.166at=11.66×9800Pa=114268Pa② 30c mH2O=13.6h cmH2Oh=30/13.6cm=2.2cm题2-2 题2-32-2.水银压力计装置如图。
《流体力学》复习提纲第一部分:基本知识第一章 流体及其主要物理性质1. 流体的概念。
2. 连续介质假设的内容,质点的概念。
3. 液体和气体相对密度的定义。
4. 密度、重度、相度密度的相互计算。
5. 体积压缩系数和体积膨胀系数的定义,写出其数学表达式。
6. 动力粘度与运动粘度的相互计算、粘度的国际单位和物理单位及单位换算。
7. 作用在流体上的力的分类:分为质量力和表面力两大类。
8. 温度对液体和气体粘性的影响规律。
9. 什么是理想流体和实际流体。
10. 牛顿内摩擦定律的内容及其两种数学表达式。
重点习题:1-1,1-4,1-5,第二章 流体静力学1. 静压强的两个重要特性是什么?2. 欧拉平衡方程及其全微分形式3. 绝对压力、相对压力(表压力)、真空度三种压力的概念。
4. 工程大气压和标准大气压的区别。
5. 静力学基本方程C pz =+γ中每一项的几何意义和物理意义是什么?6. 绝对静止和两种典型的相对静止流体(等加速水平运动和绕轴等角速旋转运动)中的压力分布规律和等压面的形状。
7. 液式测压计的计算。
8. 掌握静止流体作用在平面和曲面上的总压力的计算方法(包括总压力的大小﹑方向和作用点)等,会进行有关计算。
重点习题:2-6,2-9,2-18,2-19第三章 流体运动学与动力学基础1. 研究流体运动的两种方法:拉格朗日法和欧拉法。
2. 欧拉法表示的质点加速度公式3. 定常流与非定常流的概念4. 流线与迹线的概念5. 流量的概念及三种流量表示方法及相互换算。
6. 欧拉运动方程7. 实际流体总流伯努利方程的三条水头线的画法和意义8. 水力坡降的概念。
9. 实际流体总流伯努利方程。
10. 节流式流量计的工作原理是什么?11. 理解测速管(或皮托管)的原理和用途。
12. 泵的扬程H 的概念及其与泵有效功率泵N 的关系?13. 连续性方程反映了什么物理基本原理?质量守恒定律14. 掌握连续方程﹑总流伯努利方程和动量方程的应用,动量方程部分应会进行弯管、渐缩管和平板等受力的计算。
第三章流体运动学与动力学基础主要内容●基本概念●欧拉运动微分方程●连续性方程——质量守恒*●伯努利方程——能量守恒** 重点●动量方程——动量守恒** 难点●方程的应用第一节研究流体运动的两种方法●流体质点:物理点。
是构成连续介质的流体的基本单位,宏观上无穷小(体积非常微小,其几何尺寸可忽略),微观上无穷大(包含许许多多的流体分子,体现了许多流体分子的统计学特性)。
●空间点:几何点,表示空间位置。
流体质点是流体的组成部分,在运动时,一个质点在某一瞬时占据一定的空间点(x,y,z)上,具有一定的速度、压力、密度、温度等标志其状态的运动参数。
拉格朗日法以流体质点为研究对象,而欧拉法以空间点为研究对象。
一、拉格朗日法(跟踪法、质点法)Lagrangian method1、定义:以运动着的流体质点为研究对象,跟踪观察个别流体质点在不同时间其位置、流速和压力的变化规律,然后把足够的流体质点综合起来获得整个流场的运动规律。
2、拉格朗日变数:取t=t0时,以每个质点的空间坐标位置为(a,b,c)作为区别该质点的标识,称为拉格朗日变数。
3、方程:设任意时刻t,质点坐标为(x,y,z) ,则:x = x(a,b,c,t)y = y(a,b,c,t)z = z(a,b,c,t)4、适用情况:流体的振动和波动问题。
5、优点:可以描述各个质点在不同时间参量变化,研究流体运动轨迹上各流动参量的变化。
缺点:不便于研究整个流场的特性。
二、欧拉法(站岗法、流场法)Eulerian method1、定义:以流场内的空间点为研究对象,研究质点经过空间点时运动参数随时间的变化规律,把足够多的空间点综合起来得出整个流场的运动规律。
2、欧拉变数:空间坐标(x ,y ,z )称为欧拉变数。
3、方程:因为欧拉法是描写流场内不同位置的质点的流动参量随时间的变化,则流动参量应是空间坐标和时间的函数。
位置: x = x(x,y,z,t) y = y(x,y,z,t) z = z(x,y,z,t) 速度: u x =u x (x,y,z,t ) u y =u y (x,y,z,t ) u z =u z (x,y,z,t )同理: p =p (x,y,z,t ) ,ρ=ρ(x,y,z,t) 说明: x 、y 、z 也是时间t 的函数。
加速度:z uu y u u x u u t u a x z x y x x x x ∂∂+∂∂+∂∂+∂∂=z u u yu u xu u tu a y zy yy xy y ∂∂+∂∂+∂∂+∂∂=z u u y u u x u u t u a z z z y z x z z ∂∂+∂∂+∂∂+∂∂=全加速度=当地加速度+迁移加速度当地加速度:在一定位置上,流体质点速度随时间的变化率。
迁移加速度:流体质点所在的空间位置的变化而引起的速度变化率。
说明:两种方法具有互换性。
但由于欧拉法较简单,且本书着重讨论流场的整体运动特性。
所以,采用欧拉法研究问题。
四、流场分类1、 三元流场:凡具有三个坐标自变量的流场称为三元流场(或三维流场)。
一般来说,速度是三个坐标自变量的函数:V =V (x,y,z,t) 2、二元流场:凡具有两个坐标自变量的流场。
3、一元流场:具有一个坐标自变量的流场。
管截面A=A(l ),若人们研究的是各截面上流动的平均物理参数,则它可以简化为一元流场B=B(l , t)。
ky x j xy i xy u 5421221+-=——二维流场第二节 流体运动的基本概念一、稳定流动和不稳定流动1、不稳定流动(非定常流场):经过空间点流体质点运动参数的全部或者部分随时间而变化的流动。
(物理参数场与时间有关者)p =p (x,y,z,t ) u =u (x,y,z,t )2、稳定流动(定常流场):物理参数场与时间无关的流动。
p =p (x,y,z ) u =u (x,y,z )z uu y u u x u u a x z x y x xx ∂∂+∂∂+∂∂=z u u yu u xu u a y zy yy x y ∂∂+∂∂+∂∂=z u u y u u x u u a z z z y z xz ∂∂+∂∂+∂∂=二、迹线和流线 1、迹线:(拉格朗日法)① 定义:流体质点在一段时间内运动所经过的路线。
② 迹线特点:每个质点都有一个运动轨迹,所以迹线是一簇曲线,且只随质点不同而异,与时间无关。
③ 迹线方程:可由“欧拉法”与“拉格朗日法”互换求出。
由欧拉法: u x =u x (x,y,z,t ) u y =u y (x,y,z,t ) u z =u z (x,y,z,t )但dt dx u x =dt dy u y = dt dzu z =则——这就是迹线微分方程式。
2、流线:(欧拉法)① 定义:是某一瞬时流场中的一条曲线,该曲线上所有质点的速度矢量都和该曲线相切。
——表示流场在某一瞬时的流动方向 ② 流线的特性:不稳定流时,流线的空间方位形状随时间变化;稳定流时,流线的形状不随时间变化,并与迹线重合;流线是一条光滑曲线,既不能相交,也不能转折。
特例:点源、点汇、驻点、相切点③ 流线方程:证明:在M 点沿流线方向取有向微元长dS 设dS =idx +jdy +kdz ,M 点质点速度为u , u =iu x +ju y +ku z因为 u //dS , 所以 u ×dS =0则: z y xu dz u dy u dx == ——证毕。
④ 例题:已知:⎪⎩⎪⎨⎧=+-=+=0z y x u t y u t x u 求:t =0 时,A (-1,1)点流线的方程。
解: t y dy t x dx +-=+积分:ln(x+t)=-ln(-y+t)+C → (x+t) (-y+t)=C` 当t =0时,x =-1,y =1,代入上式得: C`=1 所以,过A (-1,1)点流线的方程为:xy =-1 ⑤ 流线的绘制方法:采用微元长切线方法 P 49三、流管、流束、总流1① 定义:在流场内画一条曲线,从曲线上每一点做流线,由许多流线围成的管子。
(人为引入的一个虚构空间) ② 特性:A. 流管内外无流体质点交换B. 稳定流时,流管形状不随时间而变 2、流束:充满在流管内部的流体微小流束:断面无穷小的流束——断面上各点运动要素相等。
3、 总流:无数微小流束的总和——所有问题都归于总流问题四、有效断面、流量和断面平均流速1、 有效断面(过流断面):流束或总流上,垂直于流线的断面。
有效断面可以是曲面或平面2、流量:单位时间内流过有效断面的流体量。
它有三种表达方法:(a )体积流量:单位时间内流过有效断面的流体体积 dQ =udA⎰=AudAQ 单位 m 3/s(b )质量流量: Q M ρ= 单位 Kg/s (c )重量流量: Q G γ= 单位 N/s3、断面平均流速V假想断面上各点流速相等,以V 表示,且其流量等于实际流速u 流过该断面的流量。
则:QudA vA A==⎰A Q AudA v A==⎰第三节 连续性方程流体的连续性方程是质量守恒定律的一个特殊形式,对于不同的液流情形,连续性方程有不同的表现形式。
质量守恒定律:对于空间固定的封闭曲面,dt 时间内流出的流体质量与流入的流体质量之差应等于封闭曲面内的流体质量的减少。
dt 时间内: 流出质量-流入质量=减少量一、一元流动(管流)连续性方程即设同一截面上的物理量均匀,因此,前面引入了断面平均流速的概念。
1、 微小流束的连续性方程 有效断面1上:dA 1、u 1、ρ1 有效断面2上:dA2、u 2、ρ2dt 时间内:(侧面无液体流入或流出) 流出质量:ρ2 u 2 dA 2dt 流入质量:ρ1 u 1 dA 1dt稳定流动,dM =0,即 流出质量=流入质量 ρ2 u 2 dA 2dt =ρ1 u 1 dA 1dt即: ρ1u 1 dA 1=ρ2u 2 dA 2——可压缩流体沿微小流束稳定流的连续性方程。
2、总流的连续性方程22211121dA u dA u A A ρρ⎰⎰=均匀管流: 22211121dA u dA u A A ⎰⎰=ρρ即2211Q Q ρρ= 或 222111A V A V ρρ=——可压缩流体稳定流沿总流的连续性方程:沿流程的质量流量保持不变。
对于不可压缩流体:ρ=C或——不可压缩流体稳定流动总流的连续性方程:沿流程的体积流量保持不变。
分流与汇流2=Q 3A 2,Q 2 二、空间运动的连续性方程本节介绍直角坐标中的连续性方程:微元分析法。
在流场中任取一微元六面体,其边长分别为dx ,dy ,dz ;a 点速度u 在三个方向的分量为u x ,u y ,u z 。
讨论分两个部分:● dt 时间内流出与流入微元体的质量之差Δm ● dt 时间前后,微元体内流体质量变化 m 1-m 21、dt 时间内流出与流入微元体的质量之差Δm x 方向:dt 时间内流入的质量:dt 时间内流出的质量:沿 x 轴方向流出和流入之差:1122m m m x-=∆同理可求:所以,dt 时间内流出与流入微元体的质量之差Δm为2、dt时间前后,微元体内流体质量变化m'∆(由于密度变化引起的)dt 时间前:dxdydz mρ=1dt3、据流体的连续流动和质量守恒:m m'∆=∆整理可得流体运动的连续性微分方程式:(1)4、公式说明:✓物理意义:单位时间内,流体流经单位体积的流出与流入之差与其内部质量变化的代数和为零。
✓(2)三、连续性方程的用途:1、反过来判断流场是否连续2、减少未知数,定义流函数、势函数3、求解复杂问题时,使方程封闭第四节 理想流体运动微分方程式及伯努利(Bernoulli )方程一、理想流体运动微分方程式(Euler 方程)它表达了理想流体受力与运动之间的动力学关系。
公式推导在流场中取微元体如图。
中心点 a压力为 p速度为 u x ,u y ,u z 。
以 x 轴方向为例推导方程。
1、受力分析:(1)因为理想流体μ=0,质量力为 Xdm ,则 单位质量流体受的质量力为:X(2)单位质量流体受的表面力(3所以,dt du x p X x=∂∂-ρ1同理:dt du y p Y y =∂∂-ρ1 dt du z p Z z=∂∂-ρ1——Euler 运动微分方程2、公式说明:(1)物理意义:作用在单位质量流体上的质量力与表面力之代数和等于加速度。
(2)适用条件:① 理想流体:无粘性、无能量消耗。
② 可压缩、不可压缩流体 ③ 稳定流、不稳定流(3)u x =u y =u z 时,得Euler 平衡微分方程 (4)方程可解性四个未知数u x ,u y ,u z ,p ,三个方程加一个连续性方程:可解。