加权复杂网络的建模研究
- 格式:pdf
- 大小:1.19 MB
- 文档页数:81

加权电网级联失效的动力学行为
贾凤玲
【期刊名称】《河北师范大学学报(自然科学版)》
【年(卷),期】2024(48)3
【摘要】根据实际IEEE118节点系统建立了加权电网的物理模型,考虑网络的电气特征,提出了基于负载容量模式下的级联失效动力学模型,同时理论推导容忍参数和系统调整系数之间的关系,并借助数值仿真验证了理论结果,进而研究了不同攻击方式对电网动力学弹性的影响.研究结果表明,不同攻击策略下加权电网的容量参数取值相差较大.
【总页数】5页(P253-257)
【作者】贾凤玲
【作者单位】成都师范学院数学学院
【正文语种】中文
【中图分类】O322;O157.5;TP393.0
【相关文献】
1.考虑级联失效的加权复杂网络鲁棒性分析
2.加权无标度网络的级联失效模型
3.有向加权供应链网络级联失效的抗毁性研究
4.基于加权网络的城市轨道交通网络特性与级联失效分析
5.基于加权耦合映像格子的拥堵道路网络级联失效研究
因版权原因,仅展示原文概要,查看原文内容请购买。



基因调控网络的建模和分析方法一、引言基因调控网络是生物学研究中非常重要的一部分。
它描述了基因之间相互作用的复杂网络,从而形成了一个生命体系中细胞的运作方式。
基因调控网络的研究不仅可以揭示基因的功能和调控机制,还可以深化人们对生命体系的理解。
因此,基因调控网络的建模和分析方法是当前生命科学中颇有前景的研究领域。
二、基因调控网络的概述基因调控网络是由基因和转录因子之间相互作用构成的复杂网络,它是细胞内基因表达的调节机制。
基因调控网络可以分为转录因子与核苷酸序列相结合,因而影响基因表达水平的转录调控网络和转录因子之间相互作用以调控基因表达模式的蛋白调控网络。
基因调控网络分析的目标在于揭示基因间的关系以及在整体网络层面上的调控机理。
在此基础上,可以进一步对某些特定基因的表达进行预测和干预。
三、基因调控网络的建模方法基因调控网络的建模方法是生物信息学领域中的重要方法之一。
它根据基因表达数据和相关的生物信息学数据,将基因和转录因子之间的相互作用建模为一个复杂网络。
常见建模方法包括基于微阵列或RNA测序技术的共表达网络,基于转录因子与基因间的互作数据的转录因子调控网络和机器学习技术的预测模型。
共表达网络是基于基因表达模式之间的相关性建模出来的网络,其中每个节点代表一个基因,每条边代表两个节点之间的相关性。
共表达网络的构建和分析可以通过基本的图论思想来完成。
转录因子调控网络则是通过转录因子与基因之间的物理相互作用信息建模出来的。
其中每个节点代表一个基因,每条边代表一个转录因子与一个基因之间的联系。
机器学习技术的预测模型是将先前获得的基因数据和相关的生物信息学数据作为输入,并建立预测模型,以预测新数据的基因表达量等数据信息。
四、基因调控网络的分析方法基因调控网络的分析是为了发现网络中的特点和规律,进一步解释基因调控网络在生物体系中的作用。
基因调控网络的分析方法包括网络拓扑结构分析、模块发现、基因挖掘和网络优化等。
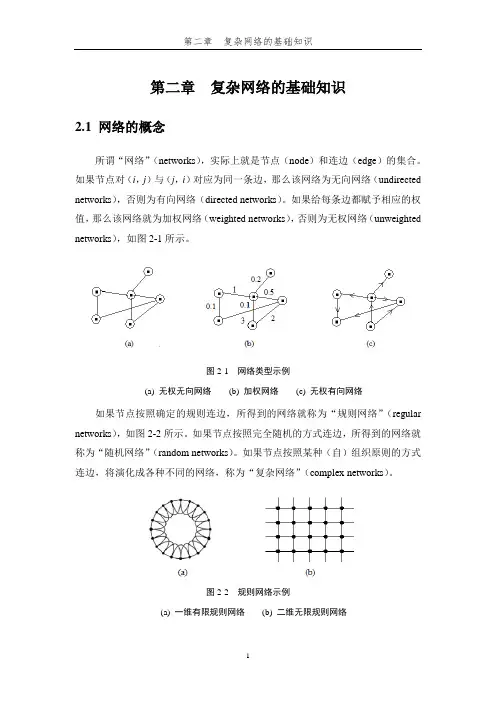
第二章复杂网络的基础知识2.1 网络的概念所谓“网络”(networks),实际上就是节点(node)和连边(edge)的集合。
如果节点对(i,j)与(j,i)对应为同一条边,那么该网络为无向网络(undirected networks),否则为有向网络(directed networks)。
如果给每条边都赋予相应的权值,那么该网络就为加权网络(weighted networks),否则为无权网络(unweighted networks),如图2-1所示。
图2-1 网络类型示例(a) 无权无向网络(b) 加权网络(c) 无权有向网络如果节点按照确定的规则连边,所得到的网络就称为“规则网络”(regular networks),如图2-2所示。
如果节点按照完全随机的方式连边,所得到的网络就称为“随机网络”(random networks)。
如果节点按照某种(自)组织原则的方式连边,将演化成各种不同的网络,称为“复杂网络”(complex networks)。
图2-2 规则网络示例(a) 一维有限规则网络(b) 二维无限规则网络2.2 复杂网络的基本特征量描述复杂网络的基本特征量主要有:平均路径长度(average path length )、簇系数(clustering efficient )、度分布(degree distribution )、介数(betweenness )等,下面介绍它们的定义。
2.2.1 平均路径长度(average path length )定义网络中任何两个节点i 和j 之间的距离l ij 为从其中一个节点出发到达另一个节点所要经过的连边的最少数目。
定义网络的直径(diameter )为网络中任意两个节点之间距离的最大值。
即}{max ,ij ji l D = (2-1) 定义网络的平均路径长度L 为网络中所有节点对之间距离的平均值。
即∑∑-=+=-=111)1(2N i N i j ij lN N L (2-2)其中N 为网络节点数,不考虑节点自身的距离。





一种不确定性复杂网络的定义及统计特征研究曹黎侠【摘要】现实网络的节点具有不确定性,边的连接具有不可分辨性,现有研究运用粗糙集理论解决了某些特定的复杂网络某一方面的问题,但没有提升到通用的网络模式的高度,形成一种完整的理论体系满足不确定性复杂网络研究的需要.提出了一种数学化的粗糙复杂网络的定义,给出了下近似粗糙复杂网络、上近似粗糙复杂网络、复杂网络的粗糙度等概念;定义了粗糙复杂网络的平均距离区间、粗集聚系数、粗糙介数等网络的静态几何特征,研究了粗糙复杂网络的加权度及其度分布.最后运用粗糙复杂网络的概念,实现了一个实际的粗糙复杂网络静态几何特征的计算,验证了相关概念的有效性和合理性.【期刊名称】《西北师范大学学报(自然科学版)》【年(卷),期】2018(054)005【总页数】7页(P28-33,43)【关键词】粗糙集;不确定性复杂网络;统计特征;粗糙复杂网络;几何特征【作者】曹黎侠【作者单位】西安工业大学理学院,陕西西安 710032【正文语种】中文【中图分类】TP399;O159近年来,科学界发现大量的真实网络具有与规则网络和随机网络都不相同的特征,并将这种无规律的网络称为复杂网络[1-4].钱学森认为,具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络称为复杂网络.复杂网络虽然已经众所周知,但目前还没有一个严格的定义[5-6].那么怎么判断一个网络是否是复杂网络呢?文献[7-10]指出,复杂网络一般具有结构复杂、网络进化、连接多样性、动力学复杂性、节点多样性和多重复杂性融合等特征.近几年来,大量关于复杂网络的文章发表在Science,Nature,PRL,PNAS等国际一流刊物上,说明复杂网络已经成为一个新兴的研究热点[11-17].目前国内外关于复杂网络的研究主要集中在复杂网络建模、同步、控制、博弈、传播、节点重要性指标、传播动力学和鲁棒性分析等方面[18-21].但是,所有这些研究成果都是针对节点具有确定性和边的连接信息具有完全性的确定性复杂网络的.一些现实网络往往节点具有不确定性,边的连接具有不可分辨性.如在电影演员合作网络中,默认电影演员是确定的,研究其相互之间合作的一个复杂网络;而实际上某一个演员他都会与哪些演员合作,与他合作的这些演员又与谁合作,事先都是不确定的;另外,一个演员是否与另一个演员合作或成为潜在的合作者,这些信息也是不可分辨的,这样的复杂网络定义为粗糙复杂网络,这样的电影演员合作网络称为粗糙电影演员合作网络.遗憾的是,到目前为止还很少有基于粗糙集[19]的不完全信息复杂网络的相关研究成果.文献[20]将粗糙集和传统图论相结合,给出基于粗糙集思想的粗糙图的定义,但是并没有把粗糙图与现实的复杂网络相对应;文献[21]给出粗糙属性图的概念,并对粗糙属性图的粗糙特性进行分析,得出粗糙属性图的精度与顶点和边集属性划分程度有关的结论,但这也只是对粗糙属性图所做的一些研究成果,不能完全解决不完全信息复杂网络上的问题.因此,文中提出了粗糙复杂网络的概念,实现该类复杂网络的概念和性质研究;通过构建实际的粗糙复杂网络并研究其静态几何特征,表明本文的概念设计能够满足一些实际问题的需求.1 预备知识1.1 粗糙集的基本概念粗糙集理论的主要思想就是在保持分类能力不变的前提下,通过知识约简导出问题的决策或分类规则.所谓知识约简,就是在保持知识库分类能力不变的条件下,删除其中不相关或不重要的知识.令X是U的一个子集,R为U上的一个等价关系,当X能表示成某些R基本范畴之并时,称X是R可定义的;否则称为不可定义的.R的可定义集称为R的精确集,而不可定义集称为R的粗糙集.粗糙集的下近似和正域是由那些根据知识R判断肯定属于X的U中的元素构成的集合;上近似是那些根据知识R判断可能属于X的U中的元素组成的集合;边界域是根据知识R既不能判断肯定属于X又不能肯定判断属于~X的U中元素构成的集合;负域是那些根据知识R判断肯定不属于X的U中元素组成的集合.1.2 复杂网络的统计特征文献[6]指出,刻画一个复杂网络最基本的三个特征量是度分布、集聚系数和平均距离.在复杂网络中,节点Vi的邻边数目ki称为节点Vi的度;对网络中所有节点的度求平均,得网络的平均度:k定义P(k)为度为k的节点在网络中所占的比率,称之为网络的度分布,一般用直方图描述度分布性质.节点Vi到Vj所要经历的边的最小数目称为这两个节点之间的距离;网络中所有节点对之间距离的平均值称为网络平均距离,即这里N为节点数,网络平均距离描述了网络有多小.如果节点Vi与ki个节点直接连接,这ki个节点间可能存在的最大边数为,而实际存在的边数记为Mi,则称为节点Vi的集聚系数;将该集聚系数对整个网络作平均,可得该网络的平均集聚系数:平均集聚系数是指在网络中与同一节点连接的两节点之间也相互连接的平均概率. 作为无向网络的静态特征,比较重要的概念还有介数,它反映了节点和边在整个网络中的作用和影响力,设Njl是节点Vj和Vl之间的最短路径条数,Njl(i)表示节点Vj和Vl之间的最短路径路过节点Vi的条数,则Vi的介数为Vi的介数就是网络中所有最短路径中经过该节点的数量的比例.类似地,边的介数Bij定义为网络中所有最短路径经过边eij的比例.2 粗糙复杂网络的概念与性质在电影演员关系网络中,某个演员与哪些演员合作,以及合作者的合作者是谁,都是不确定的.如果把当前收视排行榜在前十的影片的所有演员和剧务人员看作论域U,其中的电影演员组成了X;设网络中节点的关系可以在邻居之间传递,则R为U的一个等价关系,R={合作关系,朋友关系,同学关系},由于有些具有朋友关系的人同时也是合作关系或是同学关系,因此X不能表示为R基本范畴之并,即X是R的粗糙集.电影演员关系网络的顶点具有粗糙集的特点,所以被认为是粗糙顶点复杂网络.在第三方支付平台交易中,以商品和商家为节点,顾客随机浏览、收藏和购买商品,以顾客浏览点击为连接边,构成了第三方支付平台交易的复杂网络.由于顾客浏览具有很大的随机性,浏览的商品是否收藏和购买具有信息不完全性.设平台中的商品和商家的链接构成了论域U,网站上销售的某些品牌的手机及其销售商的链接组成了X;设网络中边的连接关系可以相邻传递,则R是顾客行为的选择,R={收藏,购买}.通常情况下,顾客浏览过的商品,先收藏,再从收藏品中择优购买,因此R是U上的一个等价关系,且X不能表示为R的基本范畴之并,所以第三方支付平台交易复杂网络的边集具有粗糙集的特性,是一个粗糙边复杂网络.下面从数学的角度给出粗糙复杂网络的概念,为研究问题方便,记E为网络中连接边的集合,V为网络中的节点集合,为下近似复杂网络的平均距离,为上近似复杂网络的平均距离.定义1 在复杂网络CN中,如果存在XV和RV,满足XV是顶点集UV的一个子集,RV为UV上的一个等价关系,当XV是RV的粗糙集时,网络的顶点集具有粗糙的特性,称复杂网络CN为粗糙顶点复杂网络RCNV.粗糙顶点复杂网络RCNV可利用两个精确复杂网络和近似定义,其中,复杂网络和分别称为粗糙顶点复杂网络RCNV的下近似顶点复杂网络和上近似顶点复杂网络.复杂网络对称为粗糙顶点复杂网络,即称为粗糙顶点复杂网络RCNV 中XV的RV-边界域.定义2 在复杂网络CN中,如果存在XE和RE,满足XE是边集UE的一个子集,RE为UV上的一个等价关系,当XE是RE的粗糙集时,复杂网络的边集具有粗糙的特性,这时称复杂网络CN为粗糙边复杂网络RCNE.粗糙边复杂网络RCNE可利用两个精确复杂网络和近似定义,其中,复杂网络和分别称为粗糙边复杂网络RCNE的下近似粗糙边复杂网络和上近似粗糙边复杂网络.复杂网络对称为粗糙边复杂网络,即称为粗糙边复杂网络RCNE中XE的RE-边界域.定义3 粗糙顶点复杂网络RCNV和粗糙边复杂网络RCNE通称为粗糙复杂网络;如果一个复杂网络既是粗糙顶点复杂网络RCNV,又是粗糙边复杂网络RCNE,记为RCN=(RCNV,RCNE).显然,一个复杂网络为粗糙复杂网络,则在关系RV下其顶点下近似网络和上近似网络必不相等,或者在关系RE下其边下近似网络和上近似网络必不相等,即或之一成立.定理1 给定复杂网络CN,则对任意的等价关系RV,RE,有(1)CN为精确复杂网络,当且仅当(2)CN为粗糙复杂网络,当且仅当类似于电影演员关系网络和第三方支付平台交易网络,如果一个复杂网络的顶点集具有不确定性,边集具有信息不完全性,都认为是粗糙复杂网络.和粗糙集一样,复杂网络的不确定性和信息不完全性,是由其顶点集和边集的边界域的存在而引起的,其边界域越大,精确度越低.为了更准确地表达这一点,引入粗糙复杂网络精确度的概念.定义4 设粗糙复杂网络RCNV(RCNE)的下近似复杂网络或测度与上近似复杂网络或的测度之比为粗糙顶点(或边)复杂网络的精度,记为显然,精确复杂网络的精确度为1.定义5 粗糙复杂网络RCN的精确度为粗糙顶点复杂网络RCNV的精确度和粗糙边复杂网络RCNE精确度的乘积,即α(RCN)=αV(RCNV)×αE(RCNE).定义6 称ρ(RCN)=1-α(RCN)为粗糙复杂网络的粗糙度.定理2 (1) 给定粗糙复杂网络RCN,对任意的等价关系R及X⊆U,都有0≤α(RCN)≤1,0≤ρ(RCN)≤1;(2)粗糙复杂网络RCN为精确复杂网络当且仅当α(RCN)=1,ρ(RCN)=0.证明 (1) 由粗糙复杂网络的定义1和定义2可知,⊆⊆故根据定义4和定义5可知:从而0≤α(RCN)≤1.根据定义6可得0≤ρ(PCN)≤1.(2)由定理1知,CN为精确复杂网络,当且仅当且所以由定义4~6可得α(RCN)=1,ρ(RCN)=0. 】3 粗糙复杂网络统计特征的研究描述一个复杂网络的静态几何特征,常用的指标有平均距离、集聚系数和度分布.在实际网络中,网络节点都具有一定的实际价值和地位,如第三方支付平台交易的粗糙复杂网络中,度相同的节点价格不同,带给商家的效益是不同.为了解决实际问题的需要,引入粗糙复杂网络的平均距离区间、粗集聚系数和加权度的概念. 定义7 称粗糙复杂网络RCN的下近似复杂网络和上近似复杂网络的平均距离构成的区间为粗糙复杂网络RCN的平均距离区间,记为平均距离区间描述了粗糙复杂网络边界域中节点间的平均分离程度的取值范围.定义8 设粗糙复杂网络RCN的下近似复杂网络的集聚系数为上近似复杂网络的集聚系数为称为粗糙复杂网络的粗集聚系数.粗集聚系数是指在网络中与同一节点连接的两节点之间也相互连接的平均概率的最大可能值.定义9 网络加权平均度为其中,N1为下近似网络的节点数;ωi为节点权重;ki为节点的度.定义10 下近似复杂网络的节点的邻边数目称为节点的下近似度;所有节点下近似度的加权平均称为网络的下近似加权平均度,记为上近似粗糙复杂网络的节点的邻边数目称为节点的上近似度;网络中所有节点的上近似度的加权平均称为网络的上近似加权平均度,记为其中N2为下近似网络的节点数.定义11 定义和分别为粗糙复杂网络度为k的节点在下近似复杂网络和上近似复杂网络中所占的比率,称它们分别为粗糙复杂网络下近似加权度分布和上近似加权度分布.定理3 粗糙复杂网络的下近似粗糙复杂网络与上近似粗糙复杂网络的度分布函数类型相同.证明对粗糙复杂网络RCN来说,由于⊆⊆所以下近似粗糙复杂网络的节点度与上近似粗糙复杂网络的节点度满足从而度分布对节点i来说,其下近似度增加到上近似度对下近似网络中加权度值为的节点而言,增加的频率为,而为下近似网络中所有节点加权度增加到的最大概率.因此,粗糙复杂网络的上近似分布曲线不低于它的下近似分布曲线,不高于下近似曲线的倍,且即故粗糙复杂网络的下近似粗糙复杂网络与上近似粗糙复杂网络的度分布函数类型相同. 】在实际网络中,网络加权度可以作为衡量一个节点重要性的指标,但是网络中也存在一些节点,虽然它的加权度很小,但它可能是两个社团的中间联系人,没有了它,整个网络的信息会中断.因此,引出粗糙复杂网络中的另一个重要的全局几何量——粗介数.定义12 设在粗糙复杂网络RCN的下近似复杂网络中,节点i(或边eij)的介数为或在上近似复杂网络中,节点i(或边eij)的介数为或称分别为粗糙复杂网络RCN的节点i和边eij的粗介数.显然,在粗糙复杂网络中,节点或边的粗介数是网络所有最短路径中路过节点i(或边eij)的比例.粗介数越大,节点(边)在网络中的地位越高.4 应用举例4.1 一个实际的粗糙复杂网络在第三方支付平台交易网络中,由商品和顾客浏览信息的特点构造第三方支付复杂网络,对应了粗糙集的论域U;如果规定,顾客购买商品前先收藏再在收藏品中择优购买,则顾客收藏的商品及其链接形成了上近似复杂网络,购买商品及其链接形成了下近似复杂网络,从而构建出第三方支付粗糙复杂网络.在该网络中,浏览而未收藏的商品及其链接为粗糙复杂网络的负域,收藏而未购买的商品为粗糙复杂网络的边界域,如图1所示,其中双粗白线及其链接节点为下近似网络,白线及其链接节点为边界域,黑线及其链接节点为网络负域.图1 第三方支付粗糙复杂网Fig 1Third-party payment rough network4.2 实际粗糙复杂网络的统计特征在第三方支付平台交易中,人们更多关心的是网络的局部特性,这些性质往往和复杂网络的静态几何特征相关.以2016-12-10 9:00~12:00淘宝支付平台“天猫商城”4个品牌的商品共176款手机及其相互连接的复杂网络作为研究对象,收集上近似复杂网络节点和下近似复杂网络节点的属性集,其中有效的上近似网络节点有91个,下近似网络节点52个.该粗糙复杂网络的精确度图2 第三方支付粗糙网络的下近似网络Fig 2Lower approximate network of third-party payment图2是它的下近似复杂网络.据定义11得到下近似网络图的加权度及其概率分布如表1所示.表1 下近似度的概率分布表Tab 1The approximate degree probability distributi onωiki1234567P(k)0.2880.0570.0190.0380.1350.0960.135ωiki8910 131617P(k)0.0580.0580.0580.0190.0190.019从下近似度的概率分布散点图可以看出,下近似度的概率分布曲线符合指数为负数的幂函数曲线,在双对数坐标系下这些点基本上都分布在一条斜率为负的直线附近.运用非线性回归分析得到下近似度分布的回归曲线说明该网络具有无标度网络的特性.由定义1~12可得该粗糙复杂网络的静态几何特征如下:1)RCN的平均距离区间.据定义7知,第三方支付粗糙复杂网络RCN的平均距离区间由上近似复杂网络的平均距离和下近似粗糙复杂网络的平均距离确定.在和中,任意两个节点的最短路径可由Dijkstra算法或Gephi软件来实现.在图2中,节点2到节点36的最短路径为:v2→v30→v32→v36.网络的直径为12,是节点13与45之间的最短距离.由于在RCN中连通的节点有可能在和中不连通,因此RCN 的平均距离区间有可能变得∞.RCN的平均距离区间有大有小,这表明第三方支付粗糙网络不具有小世界网络的特性.2)粗集聚系数.定义8指出,粗集聚系数是衡量网络集团化程度的参数.利用Gephi 软件,可以得到整个网络的聚类系数为0.183.即第三方支付网络聚类系数较小,说明该粗糙网络结构比较松散,商品之间发生信息交流关系并不活跃,反映了网络销售的竞争性和商业机密性.3)粗介数.定义12指出,粗介数越大,说明该节点在网络中的地位越高.在图2中,运用Dijkstra算法和介数的概念,可得图2介数最大的是节点37,即在整个粗糙复杂网络RCN中,粗介数说明节点37在粗糙复杂网络中的地位比较高.5 结论将不完全信息网络命名为粗糙复杂网络,设计出一种比较完整的理论体系,为粗糙复杂网络的舆情传播、搜索、网络博弈等问题的研究奠定了理论基础.1)基于粗糙集理论在不确定性问题处理中的优势,从数学的角度定义了不完全信息复杂网络——粗糙复杂网络,研究了它的几何特征.与以往的研究相比,本文的研究更系统、更精确,形成了比较完备的理论体系.2)构建了一个实际的粗糙复杂网络,研究了该粗糙网络的度分布,得出了该网络具有无标度网络的特性;计算了实际粗糙复杂网络的平均距离区间、粗集聚系数、粗介数,实现了本文所给概念的实际应用,说明了本文概念的有效性和合理性,也有助于加深对概念的理解.参考文献:【相关文献】[1] 汪小帆.网络科学发展研究[R].控制科学与工程科学发展报告,2014.[2] 汪小帆,李翔,陈关荣.网络科学导论[M].北京:高等教育出版社,2012.[3] HU Xi,HUANG Qian,ZHONG Xue-pan,et al.The influence of peer characteristics and technical features of a social shopping website on a consumer’s purchaseintention[J].International Journal of Information Management,2016,36(6):1218.[4] YI Jin-lim,ABDULLAH O,SHAHRUL N S,et al.Factors influencing online shopping Behavior:The Mediating Role of Purchase intention[J].Procedia Economics and Finance,2016,35:401.[5] SANDLER U.S-Lagrangian dynamics of many-body systems and behavior of social groups:Dominance and hierarchy formation[J].Physica A,2017,486:218.[6] 郭世泽,陆哲明.复杂网络基础理论[M].北京:科学出版社,2012.[7] 曹黎侠,黄光球,况湘玲.基于粗糙集理论的第三方支付平台的效益问题[J].统计与信息论坛,2016,31(1):62.[8] ANDRII S,KATRIN F.Big data analytics by automated generation of fuzzy rules for Network[J].Applied Soft Computing,2017,52:359.[9] FERRETTI S.Gossiping for resource discovering:An analysis based on complex network theory[J].Future Generation Computer Systems,2013,29(6):1631.[10] 张兰华.复杂网络建模的仿真与应用研究[D].大连:大连理工大学,2013.[11] 张强,李建华,沈迪,等.基于复杂网络的作战体系网络建模与优化研究[J].系统工程与电子技术,2015,37(5):1067.[12] 曹黎侠,黄光球,李艳.第三方支付粗糙复杂网络知识发现方法研究[J].计算机科学与探索,2016,25(8):1143.[13] BAI T,MENG Hong-bin,JIANG Qing-song.An improved method on rough set theory and application in prediction of pest attack[J].Biotechnology:An IndianJournal,2013,8(5):646.[14] 罗悠,罗军舟,李伟,等.面向网络状态的自适度用户行为评估方法[J].通讯学报,2013,34(7):71.[15] 曹黎侠,黄光球,李艳.基于网络基的粗糙复杂网络决策方法及应用[J].计算机科学与探索,2016,10(11):1601.[16] MENG Fan-rong,ZHU Mu,ZHOU Yong,et al.Local community detection in complex networks based on maximum cliques extension[J].Mathematical Problems in Engineering,2014,2014:1.[17] 朱志强.复杂网络上的信息传播[D].济南:山东大学,2014.[18] 张伟.基于复杂社会网络的网络舆情演化模型研究[D].哈尔滨:哈尔滨工业大学,2014.[19] 张文修,吴伟志,梁吉业,等.粗糙集理论与方法[M].北京:科学出版社,2001.[20] 何童,卢昌荆,史开泉.粗糙图与它的结构[J].山东大学学报(理学版),2006,41(6):46.[21] 张春英,郭景峰.Web社会网络的粗糙属性图模型及应用[J].计算机工程与科学,2014,36(3):517.。
