复杂网络9讲-加权网络

第二章复杂网络的基础知识2.1 网络的概念所谓“网络”（networks），实际上就是节点（node）和连边（edge）的集合。

如果节点对（i，j）与（j，i）对应为同一条边，那么该网络为无向网络（undirected networks），否则为有向网络（directed networks）。

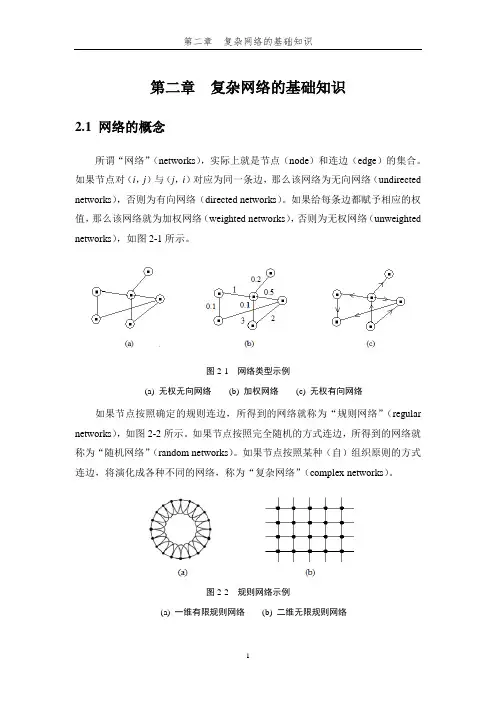
如果给每条边都赋予相应的权值，那么该网络就为加权网络（weighted networks），否则为无权网络（unweighted networks），如图2-1所示。

图2-1 网络类型示例(a) 无权无向网络(b) 加权网络(c) 无权有向网络如果节点按照确定的规则连边，所得到的网络就称为“规则网络”（regular networks），如图2-2所示。

如果节点按照完全随机的方式连边，所得到的网络就称为“随机网络”（random networks）。

如果节点按照某种（自）组织原则的方式连边，将演化成各种不同的网络，称为“复杂网络”（complex networks）。

图2-2 规则网络示例(a) 一维有限规则网络(b) 二维无限规则网络2.2 复杂网络的基本特征量描述复杂网络的基本特征量主要有：平均路径长度（average path length ）、簇系数（clustering efficient ）、度分布（degree distribution ）、介数（betweenness ）等，下面介绍它们的定义。

2.2.1 平均路径长度（average path length ）定义网络中任何两个节点i 和j 之间的距离l ij 为从其中一个节点出发到达另一个节点所要经过的连边的最少数目。

定义网络的直径（diameter ）为网络中任意两个节点之间距离的最大值。

即}{max ,ij ji l D = （2-1） 定义网络的平均路径长度L 为网络中所有节点对之间距离的平均值。

即∑∑-=+=-=111)1(2N i N i j ij lN N L （2-2）其中N 为网络节点数，不考虑节点自身的距离。

复杂网络的分析及优化随着互联网的迅速发展，越来越多的数据在网络中传输，网络结构也越来越复杂。

如何分析和优化这些复杂的网络成为一个关键问题。

本文将介绍复杂网络的分析及优化方法，包括网络拓扑结构分析、网络连通性研究、网络优化算法等。

一、网络拓扑结构分析网络的拓扑结构是指网络中节点和边的分布规律。

通过对网络拓扑结构的分析可以了解网络的整体特征和局部特征，从而深刻地认识网络内部的相互关系。

1.1 度分布度是指一个节点的直接连接数，度分布是指网络中节点度数的频率分布。

通常情况下，度分布呈现长尾分布，即有少数节点的度数非常大，而大多数节点的度数较小。

度分布的形态对网络的性质和行为有很大影响，因此度分布是复杂网络拓扑结构分析的重要指标。

1.2 聚集系数聚集系数是指网络中三角形的数量与所有可能的三角形数量的比值。

聚集系数可以用来描述网络的密集程度和连通性。

在社交网络和生物网络中，聚集系数通常比较高，而在物理和技术网络中，聚集系数较低。

1.3 特征路径长度特征路径长度是指网络中任意两个节点之间的最短路径的平均数。

网络的特征路径长度反映了网络内部连接的紧密程度，对于描述物理网络和社交网络的距离关系非常有用。

二、网络连通性研究网络连通性是指在网络结构中通过节点和边互相连接所形成的整体连通性。

网络连通性是复杂网络中最重要和最基本的特性之一。

2.1 连通性分析连通性分析是指通过对网络中节点和边的连接性进行分析，确定网络的连通性。

在无向网络中，如果任意两个节点都可以通过路径相互连接，则该网络是连通的。

在有向网络中，如果所有节点都可以到达任意另一个节点，则该网络是强连通的。

2.2 最大连通子图最大连通子图是指网络中最大的连通子集，其中任意两个节点都可以通过路径相互连接。

最大连通子图是分析网络组成和功能的关键。

2.3 非连通子图非连通子图是指网络中不属于任何连通子图的节点或边。

非连通子图可以通过增加新的节点或边，改变网络的拓扑结构，从而使网络成为连通的。

网络科学中的复杂网络理论网络科学是一门涵盖计算机科学、数学、物理学等多个学科的交叉学科，其研究的对象是网络，包括社交网络、物流网络、电力网络、金融网络等。

在网络科学的研究中，复杂网络理论是一个重要的分支，它能够帮助我们理解网络的特性和行为。

本文将从复杂网络的概念、网络拓扑结构、网络动力学、网络优化等方面介绍复杂网络理论。

一、复杂网络的概念复杂网络是由许多节点和边组成的网络，节点和边之间的关系可以是同性的或异性的，也可以是有向的或无向的。

复杂网络中的节点可以是人、公司、电力系统中的发电站等，边可以表示这些节点之间的联系，如社交网络中的朋友关系、电力系统中的输电线路等。

由于网络中的节点和边是多种多样的，所以复杂网络具有超过简单网络的复杂性和多样性。

复杂网络理论研究的是网络的结构和行为，通过分析网络节点和边之间的关系，可以揭示网络中的规律和特性。

复杂网络理论已被应用于许多领域，如社交网络分析、流行病模型、交通优化、生物信息学等。

二、网络拓扑结构网络的拓扑结构是指节点和边之间关系的模式，包括邻接矩阵、度分布、聚类系数、路径长度等几个方面。

1. 邻接矩阵邻接矩阵是一个方阵，其中的行和列分别对应网络的节点，矩阵中的元素为1表示对应节点之间有一条边，为0则表示没有边相连。

邻接矩阵是表示网络拓扑结构最简单的方式，但对于大规模网络，其密集的矩阵往往需要大量的存储空间，使得计算和分析变得困难。

2. 度分布节点的度是指该节点连接的边数。

度分布是一个度数与节点数量或概率的关系图，可以揭示网络节点之间关系的多样性。

常见的度分布包括泊松分布、幂律分布等。

幂律分布是指在一个网络中存在很少的高度连接的节点，多数节点的度数较低，这称为“无标度网络”。

无标度网络中的少数节点有着重要的作用，称为“超级节点”，它们是网络中的枢纽或关键节点。

3. 聚类系数聚类系数是指一个节点的邻居之间相互之间已经连接的比例。

聚类系数越高表示该节点的邻居之间越紧密。

第二章复杂网络的基础知识2.1 网络的概念所谓“网络”（networks），实际上就是节点（node）和连边（edge）的集合。

如果节点对（i，j）与（j，i）对应为同一条边，那么该网络为无向网络（undirected networks），否则为有向网络（directed networks）。

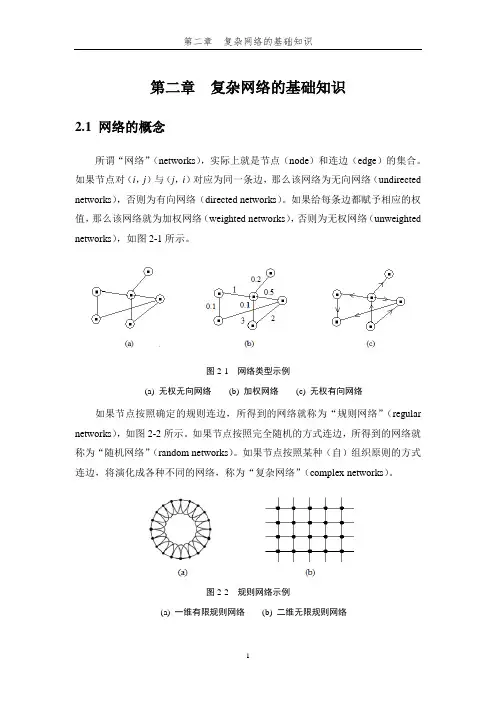
如果给每条边都赋予相应的权值，那么该网络就为加权网络（weighted networks），否则为无权网络（unweighted networks），如图2-1所示。

图2-1 网络类型示例(a) 无权无向网络(b) 加权网络(c) 无权有向网络如果节点按照确定的规则连边，所得到的网络就称为“规则网络”（regular networks），如图2-2所示。

如果节点按照完全随机的方式连边，所得到的网络就称为“随机网络”（random networks）。

如果节点按照某种（自）组织原则的方式连边，将演化成各种不同的网络，称为“复杂网络”（complex networks）。

图2-2 规则网络示例(a) 一维有限规则网络(b) 二维无限规则网络2.2 复杂网络的基本特征量描述复杂网络的基本特征量主要有：平均路径长度（average path length ）、簇系数（clustering efficient ）、度分布（degree distribution ）、介数（betweenness ）等，下面介绍它们的定义。

2.2.1 平均路径长度（average path length ）定义网络中任何两个节点i 和j 之间的距离l ij 为从其中一个节点出发到达另一个节点所要经过的连边的最少数目。

定义网络的直径（diameter ）为网络中任意两个节点之间距离的最大值。

即}{max ,ij ji l D = （2-1） 定义网络的平均路径长度L 为网络中所有节点对之间距离的平均值。

即∑∑-=+=-=111)1(2N i N i j ij lN N L （2-2）其中N 为网络节点数，不考虑节点自身的距离。

复杂网络的名词解释随着互联网的迅猛发展，我们的世界正变得越来越复杂。

在数字时代，网络已经成为了人们日常生活和工作中不可或缺的一部分。

然而，网络的本质是什么，它是如何运作的？这些问题引发了学者们对复杂网络的研究和解释。

复杂网络是网络科学中的一个重要概念，用来描述由许多相互连接的节点组成的系统。

在复杂网络中，节点可以表示个体、物体或者观察对象，而边则表示节点之间的连接或关系。

这些连接可以是社交媒体中的关注关系，互联网中的网页链接，或者是生物体内蛋白质之间的相互作用。

复杂网络的一个显著特征是其非均匀分布的拓扑结构。

相比于简单网络，如正则网络或随机网络，复杂网络的拓扑结构更加复杂多样。

大规模复杂网络常常呈现出具有高度聚集性和短平均路径长度的特点。

也就是说，网络中的节点倾向于组成局部紧密相连的群组，而通过少数边连接的节点之间的距离则很短。

在复杂网络中，节点的连接方式和模式对网络的功能和行为起着决定性的影响。

例如，一些节点连接非常多的其他节点，被称为“中心节点”或“关键节点”，它们在信息传播、网络稳定性和攻击扩散等方面起到至关重要的作用。

此外，复杂网络还具有小世界特性，即任何两个节点之间可以通过少量的中间节点快速建立联系。

这种性质使得复杂网络具有高效的信息传递能力和鲁棒性。

研究复杂网络有助于我们更好地理解和解释真实世界中许多复杂系统的行为。

它在社会学、生物学、物理学、经济学以及信息科学等领域中都有广泛的应用。

例如，在社交网络中，可以利用复杂网络的分析方法来揭示人们之间的社会关系、信息传播的路径和影响力；在生物网络中，通过研究蛋白质相互作用网络可以了解生命体系中蛋白质调控的机制和疾病的发生；在经济学中，分析金融市场网络可以评估系统的脆弱性和风险传播。

此外，复杂网络的研究不仅限于静态结构的探索，还包括网络动力学的研究。

网络动力学研究网络中节点的状态或行为随时间变化的规律。

例如，在传染病传播的研究中，网络动力学的分析可以帮助我们理解疾病传播的机制和采取相应的干预措施。

复杂网络简要介绍复杂网络是一种用于描述复杂系统中各种元素（节点）之间相互关系和连接模式的数学和图论模型。

复杂网络的研究领域涵盖了多种学科，包括物理学、计算机科学、社会学、生物学等，它们用于分析和理解各种真实世界复杂系统，如社交网络、生物网络、大气环流系统、互联网、蛋白质相互作用网络等。

复杂网络的特征和性质通常包括以下几个方面：节点和边：复杂网络由一组节点（或顶点）和连接这些节点的边（或链接）组成。

节点代表系统中的个体、元素或实体，边表示节点之间的相互关系、连接或交互。

度分布：复杂网络中的节点通常具有不同数量的连接，这被称为节点的度。

度分布描述了网络中不同节点的度数分布模式，例如是否存在高度连接的节点（所谓的“中心节点”）。

小世界性质：复杂网络中的节点通常以较短的路径相互连接，这被称为“小世界性质”，研究表明即使在大型网络中，节点之间的通信路径也相对较短。

社区结构：复杂网络中的节点通常会自发地形成一些具有内部紧密连接的子群，被称为社区。

社区结构有助于理解网络中的模块化和集团性质。

无标度性：复杂网络的度分布通常呈现无标度性质，这意味着只有少数节点具有极高的度数，而大多数节点具有较低的度数。

自组织性：复杂网络通常表现出自组织性，即它们的全局结构和性质是由局部节点之间的局部规则和相互作用自发形成的。

鲁棒性：复杂网络通常具有一定的鲁棒性，即它们能够在一定程度上抵抗节点故障或攻击而保持功能完整性。

复杂网络的研究旨在揭示各种系统之间的共性和特殊性质，并通过网络模型和分析方法来探讨这些系统的结构、功能和演化。

这种研究对于理解真实世界中的复杂系统行为、信息传播、社交动态、生物互动等方面具有广泛的应用。

2。

网络科学中的图论与复杂网络网络科学是研究网络结构和网络行为的学科，而图论和复杂网络是网络科学中的重要分支。

图论是一门数学学科，研究图及其性质，而复杂网络则是研究由大量节点和边连接而成的网络。

本文将探讨网络科学中的图论与复杂网络，并探讨它们在现实生活中的应用。

一、图论图论是研究图及其性质的数学学科。

图由节点和边组成，节点代表网络中的个体，边代表节点之间的连接。

图论主要研究图的结构、性质和算法等问题。

1. 图的基本概念在图论中，有一些基本概念需要了解。

首先是无向图和有向图。

无向图中的边没有方向，而有向图中的边有方向。

其次是度数，度数指的是与一个节点相连的边的数量。

还有连通性，如果在一个图中，任意两个节点之间都存在路径，则称该图是连通的。

2. 图的算法图论中有许多重要的算法，如最短路径算法、最小生成树算法和最大流算法等。

最短路径算法用于寻找两个节点之间最短的路径，最小生成树算法用于寻找一个连通图的最小生成树，最大流算法用于计算网络中最大的流量。

3. 图的应用图论在现实生活中有着广泛的应用。

例如，社交网络可以用图来表示，节点代表人，边代表人与人之间的关系。

通过分析社交网络的结构，可以研究社交网络中的信息传播、影响力传播等问题。

此外，图论还可以应用于交通网络、电力网络和物流网络等领域。

二、复杂网络复杂网络是由大量节点和边连接而成的网络。

与传统的简单网络不同，复杂网络具有许多独特的性质，如小世界效应、无标度性和社区结构等。

1. 小世界效应小世界效应是指在复杂网络中，任意两个节点之间的距离很短。

也就是说，通过很少的步骤，就可以从一个节点到达另一个节点。

这一性质在社交网络中尤为明显，因为人与人之间的联系往往通过共同的朋友来实现。

2. 无标度性无标度性是指复杂网络中节点的度数呈幂律分布。

也就是说，只有少数节点具有非常高的度数，而大部分节点的度数相对较低。

这种性质在许多现实网络中都存在，如互联网、社交网络和蛋白质相互作用网络等。

复杂网络的理论及应用随着科技的不断发展，人们的生活和社会组织方式也在不断变化。

在这个过程中，网络的作用越来越显著。

复杂网络作为网络科学的一支重要学科，研究的是网络的结构和性质。

通过探究网络中节点的联系及其交互关系，为许多实际问题提供了解决思路。

1. 复杂网络的理论复杂网络学理论基础主要有三个方面：图论、随机过程、统计物理学。

图论是复杂网络学理论的基础，它将复杂网络看作由节点和边构成的图。

随机过程是强大的工具，它可以描述复杂网络的动态演化。

统计物理学则为复杂网络提供了相当严密的理论基础，将网络中的节点当作对象，基于概率论和热力学的基本假设，研究网络的各种性质。

在以上基础上，复杂网络的理论发展主要包括以下几个方面：1.1. 网络的基本属性网络的基本属性包括：度数分布、聚类系数和平均路径长度。

其中，度数分布指的是每个节点拥有的链接数，而聚类系数和平均路径长度则分别描述了节点间的紧密程度和短距离程度。

1.2. 小世界效应小世界网络是指网络具有高聚类系数和短路径长度的共同特点。

研究表明，许多真实网络都具有小世界特性，表现为较高的聚集指数和较短的平均路径长度。

这种现象被称为小世界效应。

1.3. 无标度网络与节点重要性无标度网络是指网络中节点度数分布呈幂律分布。

具有该特性的网络具有重要的节点。

研究表明，少数节点在网络中的重要性远高于其他节点，这些节点被称为“关键节点”。

识别和保护这些关键节点对于网络的稳定性和鲁棒性至关重要。

1.4. 阻尼振荡阻尼振荡是复杂网络中的一种现象，它可以描述节点之间的同步现象。

研究表明，网络的结构和同步现象密切相关，不同的结构会导致不同的同步行为。

2. 复杂网络的应用复杂网络的应用广泛，尤其在社会学、生物学等领域中有着非常重要的地位。

下面分别介绍常见的应用领域。

2.1. 社交网络社交网络指的是人与人之间的联系网络。

研究表明，社交网络中的节点和联系具有很多特性，比如关闭性、传染性等。

基于这些特性，社交网络可以应用于疾病的传播、信息的传递等领域。

面向大数据的复杂网络理论与应用一、背景介绍随着信息技术的快速发展，数据已成为当今社会的一大资源。

大数据时代的到来，使得数据量呈现指数级增长。

在这种背景下，网络分析方法被广泛应用于复杂数据的分析。

复杂网络是由大量节点和连接组成的网络结构，例如社交网络、交通网络和互联网等。

复杂网络的理论和应用对于解决大规模数据的问题具有重要意义。

二、复杂网络的基本理论1. 复杂网络的表示方法复杂网络可以用图形和矩阵表示。

在图形表示中，节点表示复杂体系中的元素，边表示这些元素之间的关系。

矩阵表示法则是将复杂体系转化为一个矩阵，该矩阵中的数值表示节点与节点之间的距离或者相似程度。

2. 复杂网络的属性复杂网络的属性包括度、聚类系数和介数中心性等。

节点的度指的是连接该节点的边数，聚类系数表示相邻节点之间的联系程度，介数中心性反映一个节点在网络中的重要程度。

3. 复杂网络的模型常见的复杂网络模型包括随机网络模型、小世界网络模型和无标度网络模型等。

随机网络模型是指连接节点的方式随机分布的网络，小世界网络模型则是在随机网络的基础上，使得节点之间具备一定的距离，无标度网络模型则是建立在度分布律的基础上，节点的度数呈现幂律分布。

三、复杂网络在大数据分析中的应用1. 社交网络分析社交网络是人们在社交关系中形成的互联网络，例如微博、微信等。

社交网络分析可以对用户行为进行建模和预测，对于社交媒体的商业应用，例如用户关注度分析和用户行为分析等方面带来了巨大的商业价值。

2. 交通网络分析交通网络是人们在交通出行中形成的互联网络，例如地铁、公交、高速公路等。

交通网络分析可以预测车流量、拥堵情况和出行方案，对于城市交通管理和规划方面带来了重要的应用支持。

3. 互联网搜索引擎互联网搜索引擎是人们搜索网络信息的重要工具，例如百度、谷歌等。

在海量的数据搜索和排名方面，复杂网络分析技术可以提高搜索结果的准确性和效率。

四、面向大数据的复杂网络的未来展望复杂网络的发展已经走到了一个全面应用的时代，大数据在此背景下推进网络技术的创新和升级。

复杂网络理论是近年来引起广泛关注的一个研究领域。

它涉及了各个学科领域，如生物学、物理学、计算机科学和社会学等。

研究的是由一些元素和它们之间的相互作用构成的网络结构，这些网络结构的复杂性表现在拓扑结构、动力学规律、行为特性等方面。

的研究目标是寻找这些网络的规律与特性，为实际问题解决提供理论基础。

的历史可以追溯到20世纪50年代初，当时数学家图灵发明了图灵机，为计算机科学奠定了基础。

20世纪60年代，图论应用于实际问题解决，计算机网络开始蓬勃发展。

20世纪90年代初，小世界模型被提出，从而引起了学术界的广泛关注。

之后，逐渐形成。

近年来，随着大数据和人工智能等技术的发展，的重要性不断提升。

的核心问题是对网络结构、动力学规律、性质特性进行研究。

网络结构是指有多个节点组成的网络中节点之间的连接模式，包括邻接关系、边权重、网络密度等。

复杂网络的拓扑结构可以分为随机网络、小世界网络、尺度自相似网络和重级网络等不同类别。

随机网络是指节点的连接方式是随机的，小世界网络是指节点之间具有较短的路径长度和高度聚集的特点，尺度自相似网络是指节点在不同的尺度下表现出类似的结构和性质，重级网络是指节点具有不同的重要性等级。

动力学规律是指节点之间的状态变化以及网络结构的演化过程。

复杂网络的动力学规律包括网络同步、分化、演化等。

同步是指节点之间的状态能够达到一致，分化是指节点之间具有不同的状态，演化是指网络结构和节点状态随时间的推移而发生变化。

性质特性是指网络结构和动力学规律的综合表现，包括节点度分布、聚类系数、网络离心率、介数中心性等。

节点度分布是指节点之间的连接模式，聚类系数是指节点聚合形成的团簇，网络离心率是指网络结构的中心性程度，介数中心性是指节点在网络中的重要程度等。

在各个领域应用广泛。

在生物学中，被用于描述蛋白质相互作用网络、神经元网络等，从而揭示生物系统的相关规律。

在物理学中，被用于解释电力网络、交通网络等，从而实现优化设计和运行管理。

金融风险评估中复杂网络分析技术的使用方法与模型调整技巧随着金融市场的复杂性和风险的增加，金融机构对于风险评估和管理的需求也日益迫切。

在这个背景下，复杂网络分析技术成为了金融风险评估中的重要工具。

通过构建金融系统的复杂网络模型，可以识别并量化系统内部的相关性、脆弱性和传染性。

本文将介绍金融风险评估中复杂网络分析技术的使用方法，并探讨模型调整的技巧。

一、复杂网络分析技术的使用方法1. 数据收集与处理在运用复杂网络分析技术进行金融风险评估之前，首先需要收集、整理和处理相关数据。

这些数据包括金融资产的价格和交易数据等。

需要注意的是，数据的质量和准确性对于评估结果的准确性至关重要。

2. 构建网络模型基于收集到的金融数据，可以构建一个复杂网络模型，其中金融资产被视为节点，而节点间的交易和关联关系则以边来表示。

在构建网络模型时，需要考虑选择适当的网络拓扑结构，如无向网络、有向网络、加权网络等。

3. 计算网络指标一旦构建了复杂网络模型，就可以计算各种网络指标来衡量金融系统的特性和风险水平。

常用的指标包括节点的度中心性、介数中心性和特征向量中心性，以及网络的聚集系数、平均路径长度和小世界属性等。

这些指标可以揭示出金融系统内部的关联性和传染性，为风险评估提供线索。

4. 评估脆弱性脆弱性是指金融系统面临的外部或内部冲击时，系统容易受到破坏或传染的程度。

通过复杂网络分析技术，可以识别和评估金融系统的脆弱性。

例如，可以通过度中心性或其他相关指标来识别那些在网络中具有关键作用的节点，这些节点一旦遭受到损害或失败，可能会导致整个系统的崩溃。

二、模型调整的技巧1. 选择适当的网络模型不同的金融系统可能具有不同的特性和结构，因此，在进行复杂网络分析时，需要选择适合该金融系统的网络模型。

一般来说，无向网络可以用于描述金融资产之间的共同涨跌关系，有向网络可以用于描述资金的流动关系，而加权网络则可以用于考虑不同资产的重要性和联系强度。