八年级数学下册《勾股定理》练习题及答案(人教版)

勾股定理

练习题

温故而知新： 1.勾股定理

直角三角形两条直角边a,b的平方和等于斜边c的平方，即a2+b2=c2.

2.勾股定理的验证

勾股定理的证明方法很多，据说已有400余种，其证明的内涵极其丰富.常用的证法是面积割补法，如图所示.

3.直角三角形的性质

两锐角互余（角的关系）、勾股定理（边的关系），30°角所对的直角边等于斜边的一半（边角关系），这些性质在求线段的长度、证明线段倍分关系、证明线段平方关系等方面有广泛的应用.

例1 （2013·安顺）如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢,小鸟至少飞行（ ）

米 米

米 米

解析：小鸟飞行的最短路线如图所示为线段AB；过点A向10米高的树作垂线，垂足为C，则易知AC=8米，BC=10-4=6（米）；根据勾股定理可得

AB=22ACBC=2286=10（米）.

答案：B

小结：在解决实际问题时，往往根据题意把实际问题转化为数学问题，构造直角三角形利用勾股定理来解决.有时根据需要巧设未知数，借助勾股定理列方程求解，常可使问题简便.

例2 （2013·衢州）如图，将一个有45°角的三角板的直角顶点放在一张宽为3cm的矩形纸带边沿上，另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30°角，则三角板最大边的长为（ ）

cm cm 2 cm 2 cm

解析：如图所示在图中标上字母，过点A作AD⊥BD，

垂足为D，则AD=3 cm；

因为∠ABD=30°，所以AB=2AD=6 cm；

又△ABC是等腰直角三角形，故BC=AB=6 cm，根据勾股定理可得AC=22ABBC=2266=62（cm）

答案：D

小结：在直角三角形中，30°角所对的直角边等于斜边的一半，45°的直角三角形中，斜边是直角边的2倍.

温故而知新：

1.勾股定理

直角三角形两条直角边a,b的平方和等于斜边c的平方，即a+b=c.

2.勾股定理的验证

勾股定理的证明方法很多，据说已有400余种，其证明的内涵极其丰富.常用的证法是面积割补法，如图所示.

3.直角三角形的性质

两锐角互余（角的关系）、勾股定理（边的关系），30°角所对的直角边等于斜边的一半（边角关系），这些性质在求线段的长度、证明线段倍分关系、证明线段平方关系等方面有广泛的应用.

例1 如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢,小鸟至少飞行（ ）

A.8米 B.10米

C.12米 D.14米

解析：小鸟飞行的最短路线如图所示为线段AB；过点A向10米高的树作垂线，垂足为C，则易知AC=8米，BC=10-4=6（米）；根据勾股定理可得

AB=22ACBC=2286=10（米）.

答案：B

小结：在解决实际问题时，往往根据题意把实际问题转化为数学问题，构造直角三角形利用勾股定理来解决.有时根据需要巧设未知数，借助勾股定理列方程求解，常可使问题简便.

例2 如图，将一个有45°角的三角板的直角顶点放在一张宽为3cm的矩形纸带边沿上，另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30°角，则三角板最大边的长为（ ）

A.3 cm B.6 cm

C.3 cm D.6 cm

解析：如图所示在图中标上字母，过点A作AD⊥BD，

垂足为D，则AD=3 cm；

因为∠ABD=30°，所以AB=2AD=6 cm；

又△ABC是等腰直角三角形，故BC=AB=6 cm，根据勾股定理可得AC=22ABBC=2266=62（cm）

答案：D

小结：在直角三角形中，30°角所对的直角边等于斜边的一半，45°的直角三角形中，斜边是直角边的2倍.

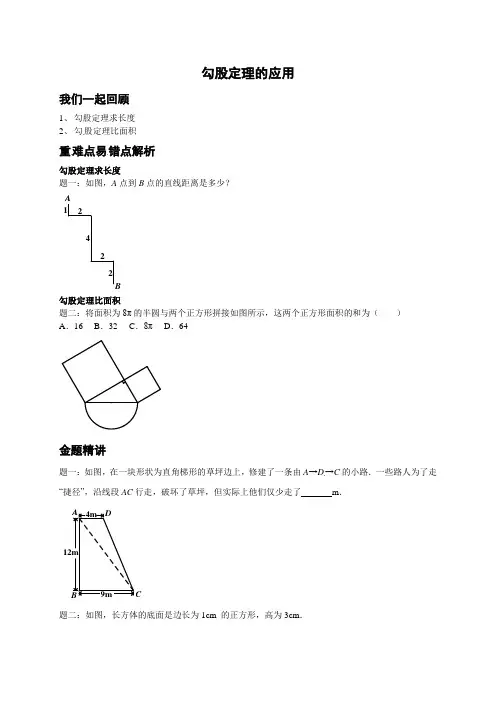
勾股定理的应用

我们一起回顾

1、 勾股定理求长度

2、 勾股定理比面积

重难点易错点解析

勾股定理求长度

题一：如图，A点到B点的直线距离是多少？

22421BA

勾股定理比面积

题二：将面积为8π的半圆与两个正方形拼接如图所示，这两个正方形面积的和为（ ）

A．16 B．32 C．8π D．64

金题精讲

题一：如图，在一块形状为直角梯形的草坪边上，修建了一条由A→D→C的小路．一些路人为了走“捷径”，沿线段AC行走，破坏了草坪，但实际上他们仅少走了_______m．

4m12m9mDABC

题二：如图，长方体的底面是边长为1cm 的正方形，高为3cm． （1）如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，请利用侧面展开图计算所用细线最短需要多长？

（2）如果从点A开始缠绕2圈到达点B，那么所用细线最短需要多长？

BA

题三：直角三角形ABC的面积为20，在AB的同侧分别以AB、BC、CA为直径作三个半圆，求阴影部分面积．

BAC

题四：如图，一架2.5米长的梯子斜立在竖直的墙上，此时梯足B距底端O为0.7米，如果梯子顶端下滑0.4米，则梯子将滑出多少米？

B'A'BAO

思维拓展 题一：下图是由一连串直角三角形演化而成的，其中OA1=A1A2=A2A3=…=A7A8=1，如果把图中的直角三角形继续作下去，那么线段OA1，OA2，…OA25中有（ ）条的长度为正整数．

A．3 B．4 C．5 D．6

A2OA1A3A4A5A6A7A8

学习提醒

重点：

勾股定理求长度——构造直角三角形，进行计算

勾股定理比面积——寻找平方间的关系 勾股定理的应用

讲义参考答案

重难点易错点解析

题一：65．

考点：勾股定理求长度：构造直角三角形，进行计算

题二：D．

考点：勾股定理比面积：寻找平方间的关系

金题精讲

题一：2．

考点：勾股定理求长度

题二：（1）5cm；（2）73cm．

《勾股定理》单元测试题

一、选择题（每题3分，共30分）

1.分别以下列五组数为一个三角形的边长：①6，8，10；②13，5，12 ③1，2，3；④9，40，41；⑤321，421，521.其中能构成直角三角形的有（ ）组

2.已知△ABC中，∠A＝21∠B＝31∠C，则它的三条边之比为（ ）

∶1∶2 ∶3∶2 ∶2∶3 ∶4∶1

3.已知直角三角形一个锐角60°，斜边长为2，那么此直角三角形的周长是（ ）

A. 25 C. 3+2 D. 33

4.如果梯子的底端离建筑物5米，13米长的梯子可以达到建筑物的高度是（ ）

米 米 米 米

5.放学以后，小明和小刚从学校出发，分别沿东南方向和西南方向回家，若小明和小刚行走的速度都是40米/分，小明用15分钟到家，小刚用20分钟到家，小明家和小刚家的距离为（ ）

米 米 米 D.不能确定

6.已知如图1，长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（ ） A. 6cm2 B. 8cm2 C. 10cm2 D. 12cm2

7.如图2，分别以直角△ABC的三边AB，BC，CA为直径向外作半圆.设直线AB左边阴影部分的面积为S1，右边阴影部分的面积和为S2，则（ ）

＝S2 ＜S2 ＞S2 D.无法确定

8.在△ABC中，∠C＝90°，周长为60，斜边与一直角边比是13∶5，则这个三角形三边长分别是（ ）

，4，3 ，12，5 ，8，6 ，24，10

9.如图3所示，AB＝BC＝CD＝DE＝1，AB⊥BC，AC⊥CD，AD⊥DE，则AE等于（ ）

八年级数学期末复习

勾股定理

知识结构图

本章知识在考试中主要考查勾股定理的运用，在几何图形中或实际问题中，利用勾股定理求线

段长是常考题型，特殊题型有平面图形的折叠问题．

重难点突破

重难点1　勾股定理的证明

【例1】　以图1中的直角三角形为基础，可以构造出以a，b为底，以a＋b为高的直角梯形（如

图2），请你利用图2，验证勾股定理．

图1 图2

【思路点拨】　利用梯形面积的两种算法列出等式证明．

【解答】　勾股定理的证明是用面积法证明恒等式的方法，通过不同的方式表示同一个图形的面积．

1．如图是用硬纸板做成的四个全等的直角三角形（两直角边长分别是a，b，斜边长为c）和一个

边长为c的正方形，请你将它们拼成一个能证明勾股定理的图形．

（1）画出拼成图形的示意图；

（2）证明勾股定理．

重难点2　勾股定理及其逆定理

【例2】　如图，每个小正方形的边长为1.

（1）求四边形ABCD的周长；

（2）求证：∠C＝90°.

【思路点拨】　（1）利用勾股定理求出四边形的各边长；（2）求出△BCD的三边长，利用勾股定

理的逆定理证明．【解答】　

正方形网格中的两个格点之间的距离可以用勾股定理求出，勾股定理的逆定理是证明一个角等

于90°的一种思路，本题的第（2）问还可以通过两个三角形来证明．

2．（2017·南宁月考）在Rt△ABC中，∠C＝90°，AB＝10，BC＝6，则AC＝____________.

3．如图，四边形ABCD中，AB＝20，BC＝15，CD＝7，AD＝24，∠B＝90°，求证：∠A＋∠C＝180°.

重难点3　勾股定理的实际应用

【例3】　如图，小丽想知道自家门前小河的宽度，于是她按以下方法测出了如下数据：小丽在河

岸边选取点A，在点A的对岸选取一个参照点C，测得∠CAD＝30°；小丽沿岸向前走30 m选取点B

，并测得∠CBD＝60°.请根据以上数据，用你所学的数学知识，帮小丽计算小河的宽度．

【思路点拨】　过点C作CE⊥AD于点E.先根据等腰三角形的判定得出BC的长，再在Rt△BCE中

1 温故而知新：

1.勾股定理

直角三角形两条直角边a,b的平方和等于斜边c的平方，即a+b=c.

2.勾股定理的验证

勾股定理的证明方法很多，据说已有400余种，其证明的内涵极其丰富.常用的证法是面积割补法，如图所示.

3.直角三角形的性质

两锐角互余（角的关系）、勾股定理（边的关系），30°角所对的直角边等于斜边的一半（边角关系），这些性质在求线段的长度、证明线段倍分关系、证明线段平方关系等方面有广泛的应用.

例1 如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢,小鸟至少飞行（ ）

A.8米 B.10米

C.12米 D.14米

解析：小鸟飞行的最短路线如图所示为线段AB；过点A向10米高的树作垂线，垂足为C，则易知AC=8米，BC=10-4=6（米）；根据勾股定理可得

AB=22ACBC=2286=10（米）.

答案：B

小结：在解决实际问题时，往往根据题意把实际问题转化为数学问题，构造直角三角形利用勾股定理来解决.有时根据需要巧设未知数，借助勾股定理列方程求解，常可使问题简便.

2

例2

如图，将一个有45°角的三角板的直角顶点放在一张宽为3cm的矩形纸带边沿上，另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30°角，则三角板最大边的长为（ ）

A.3 cm B.6 cm

C.3 cm D.6 cm

解析：如图所示在图中标上字母，过点A作AD⊥BD，

垂足为D，则AD=3 cm；

因为∠ABD=30°，所以AB=2AD=6 cm；

又△ABC是等腰直角三角形，故BC=AB=6 cm，根据勾股定理可得AC=22ABBC=2266=62（cm）

答案：D

小结：在直角三角形中，30°角所对的直角边等于斜边的一半，45°的直角三角形中，斜边是直角边的2倍.

《勾股定理》的说课稿

尊敬的各位评委、各位教师：

你们好！今天我说课的课题是《勾股定理》。本课选自九年义务教育人教版八年级下册初中数学第十七章第一节的第一课时。

下面我从教学背景分析与处理、教学策略、教学流程等方面对本课的设计进行说明。

一、教学背景分析

1、教材分析

本节课是学生在已经掌握了直角三角形有关性质的基础上进行学习的，通过2002年国际数学家大会的会徽图案，引入勾股定理，进而探索直角三角形三边的数量关系，并应用它解决问题。学好本节不仅为下节勾股定理的逆定理打下良好基础，而且为今后学习解直角三角形奠定基础,在实际生活中用途很大。勾股定理是直角三角形的一条非常重要的性质，是几何中一个非常重要的定理，它揭示了直角三角形三边之间的数量关系，将数与形密切地联系起来，它有着丰富的历史背景，在理论上占有重要的地位。

2、学情分析

通过前面的学习，学生已具备一些平面几何的知识，能够进行一般的推理和论证，但如何通过拼图来证明勾股定理，学生对这种解决问题的途径还比较陌生，存在一定的难度，因此，我采用直观教具、多媒体等手段，让学生动手、动口、动脑，化难为易，深入浅出，让学生感受学习知识的乐趣。

3、教学目标：

根据八年级学生的认知水平，依据新课程标准和教学大纲的要求，我制定了如下的教学目标：

知识与能力：了解勾股定理的发现过程，掌握勾股定理的内容，会用面积法证明勾股定理；培养在实际生活中发现问题总结规律的意识和能力．

过程与方法：通过创设情境，导入新课，引导学生探索勾股定理，并应用它解决问题，运用了观察、演示、实验、操作等方法学习新知。

情感态度价值观：感受数学文化，激发学生学习的热情，体验合作学习成功的喜悦，渗透数形结合的思想。

4、教学重点、难点

通过分析可见，勾股定理是平面几何的重要定理，有着承上启下

的作用，在今后的生活实践中有着广泛应用。因此我确定本课的教学

重点为探索和证明勾股定理．

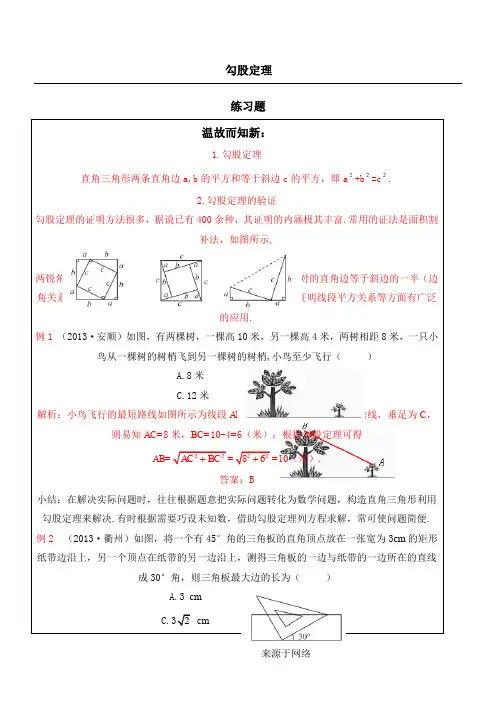
来源于网络 勾股定理

练习题

温故而知新：

1.勾股定理

直角三角形两条直角边a,b的平方和等于斜边c的平方，即a2+b2=c2.

2.勾股定理的验证

勾股定理的证明方法很多，据说已有400余种，其证明的内涵极其丰富.常用的证法是面积割补法，如图所示.

3.直角三角形的性质

两锐角互余（角的关系）、勾股定理（边的关系），30°角所对的直角边等于斜边的一半（边角关系），这些性质在求线段的长度、证明线段倍分关系、证明线段平方关系等方面有广泛的应用.

例1 （2013·安顺）如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢,小鸟至少飞行（ ）

A.8米 B.10米

C.12米 D.14米

解析：小鸟飞行的最短路线如图所示为线段AB；过点A向10米高的树作垂线，垂足为C，则易知AC=8米，BC=10-4=6（米）；根据勾股定理可得

AB=22ACBC=2286=10（米）.

答案：B

小结：在解决实际问题时，往往根据题意把实际问题转化为数学问题，构造直角三角形利用勾股定理来解决.有时根据需要巧设未知数，借助勾股定理列方程求解，常可使问题简便.

例2 （2013·衢州）如图，将一个有45°角的三角板的直角顶点放在一张宽为3cm的矩形纸带边沿上，另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30°角，则三角板最大边的长为（ ）

A.3 cm B.6 cm

C.32 cm D.62 cm

来源于网络 解析：如图所示在图中标上字母，过点A作AD⊥BD，

垂足为D，则AD=3 cm；

因为∠ABD=30°，所以AB=2AD=6 cm；

又△ABC是等腰直角三角形，故BC=AB=6 cm，根据勾股定理可得AC=22ABBC=2266=62（cm）

第 1 页 共 4 页

第十七章 勾股定理

17.1 勾股定理

第1课时 勾股定理

学习目标：1.经历勾股定理的探究过程，了解关于勾股定理的一些文化历史背景，会用

面积法来证明勾股定理，体会数形结合的思想；

2.会用勾股定理进行简单的计算.

重点：用面积法来证明勾股定理，体会数形结合的思想.

难点：会用勾股定理进行简单的计算.

一、知识回顾

1.网格中每个小正方形的面积为单位1,你能数出图中的正方形A、B 的面积吗？你又能想到什么方法算出正方形C的面积呢？

ABCCBA

自主学习 教学备注

学生在课前完成自主学习部分

配套PPT讲授

1.情景引入

（见幻灯片3-5）

方法1：补形法(把以斜边为边长的正方形补成各

边都在网格线上的正方形）：

左图：Sc=__________________________;

右图：Sc=__________________________.

方法2：分割法(把以斜边为边长的正方形分割成

易求出面积的三角形和四边形）：

左图：Sc=__________________________;

右图：Sc=__________________________.

第 2 页 共 4 页 ABCCBA

一、要点探究 探究点1：勾股定理的认识及验证

想一想 1.2500年前，毕达哥拉斯去老朋友家做客，看到他朋友家用等腰三角形砖铺成的地面，联想到了正方形A，B和C面积之间的关系，你能想到是什么关系吗？

2.右图中正方形A、B、C所围成的等腰直角三角形三边之间有什么特殊关系？

3.在网格中一般的直角三角形，以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系？(每个小正方形的面积为单位1)

4.正方形A、B、C 所围成的直角三角形三条边之间有怎样的特殊关系？

思考 你发现了直角三角形三条边之间的什么规律？你能结合字母表示出来吗？

八年级数学勾股定理练习题及答案

TTA standardization office【TTA 5AB- TTAK 08- TTA 2C】

勾股定理

练习题

温故而知新：

1.勾股定理

直角三角形两条直角边a,b的平方和等于斜边c的平方，即a2+b2=c2.

2.勾股定理的验证

勾股定理的证明方法很多，据说已有400余种，其证明的内涵极其丰富.常用的证法是面积割补法，如图所示.

3.直角三角形的性质

两锐角互余（角的关系）、勾股定理（边的关系），30°角所对的直角边等于斜边的一半（边角关系），这些性质在求线段的长度、证明线段倍分关系、证明线段平方关系等方面有广泛的应用.

例1 （2013·安顺）如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢,小鸟至少飞行（ ）

米 米

米 米

解析：小鸟飞行的最短路线如图所示为线段AB；过点A向10米高的树作垂线，垂足为C，则易知AC=8米，BC=10-4=6（米）；根据勾股定理可得

AB=22ACBC=2286=10（米）.

答案：B

小结：在解决实际问题时，往往根据题意把实际问题转化为数学问题，构造直角三角形利用勾股定理来解决.有时根据需要巧设未知数，借助勾股定理列方程求解，常可使问题简便.

例2 （2013·衢州）如图，将一个有45°角的三角板的直角顶点放在一张宽为3cm的矩形纸带边沿上，另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30°角，则三角板最大边的长为（ ）

cm cm

2 cm 2 cm

解析：如图所示在图中标上字母，过点A作AD⊥BD，

垂足为D，则AD=3 cm；

因为∠ABD=30°，所以AB=2AD=6 cm；

人教版八年级下册数学第十七章 勾股定理含答案

一、单选题(共15题，共计45分)

1、在 中，∠C=90°，sinA= ，则tanA=（ ） A. B. C.1 D.

2、如图，正方形ABCD的边长为4，点E在对角线BD上，且∠BAE=22.5°，EF⊥AB，垂足为F，则EF的长为（ ）

A.1 B. C. D.

3、如图，在梯形ABCD中，AB∥CD，∠D=90°，AD＝CD＝4，AB=1，F为AD的中点，则F到BC的距离是（ ）．

A.1 B.2 C.4 D.8

4、直角三角形中一直角边的长为9，另两边为连续自然数，则直角三角形的周长为（ ）

A.90 B.120 C.121 D.不能确定

5、如图，在Rt△ABC中，∠ACB=90°，BD平分∠ABC．若CD=3，BC+AB=16，则△ABC的面积为（ ）

A.16 B.18 C.24 D.32

6、在平面直角坐标系中,点A,B的坐标分别为(－6,0),(0,8). 以点A为圆心,以AB长为半径画弧交x轴于点C,则点C的坐标为（ ）.

A.(6,0) B.(4,0) C.(6,0)或(-16,0) D.(4,0)或(-16,0)

7、如图，平面直角坐标系中，A点坐标为 ，点 在直线

上运动，设 的值为 ，则下面能够大致反映w与m的函数关系的图象是（ ）

A. B. C.

D.

8、如图，已知由16个边长为1的小正方形拼成的图案中，有五条线段PA、PB、PC、PD、PE，其中长度是有理数的有 （ ）

A.1条 B.2条 C.3条 D.4条

9、在直角三角形ABC中，斜边AB=1，则AB²+BC²+AC²=（ ）

A.2 B.4 C.6 D.8

10、如图，在4×4的正方形方格图形中，小正方形的顶点称为格点，△ABC的顶点都在格点上，则图中∠ABC的余弦值是（ ）

第 1 页 共 20 页 人教版八年级数学下册《利用勾股定理解决折叠问题的技巧》练习题(附带答案）

类型一 利用勾股定理解决三角形的折叠问题

1．如图 △ABC中 ∠ACB＝90° AC＝8 BC＝6 将△ADE沿DE翻折

使点A与点B重合 则CE的长为 ．

思路引领：设CE＝x 则AE＝BE＝8﹣x 在Rt△BCE中 由勾股定理可得62+x2＝（8﹣x）2 即可解得答案．

解：设CE＝x 则AE＝BE＝8﹣x

在Rt△BCE中 BC2+CE2＝BE2

∴62+x2＝（8﹣x）2

解得x=74

故答案为：74．

总结提升：本题考查直角三角形中的折叠问题 解题的关键是掌握折叠的性质 熟练应用勾股定理列方程解决问题．

2．（2021秋•介休市期中）如图所示 有一块直角三角形纸片 ∠C＝90° AC＝8cm BC＝6cm 将斜边AB翻折 使点B落在直角边AC的延长线上的点E处 折痕为AD 则CE的长为 cm．

思路引领：根据勾股定理可将斜边AB的长求出 根据折叠的性质知 AE＝AB 已知AC的长 可将CE的长求出．

解：在Rt△ABC中 第 2 页 共 20 页 ∵∠C＝90° AC＝8cm BC＝6cm

∴AB=√𝐴𝐶2+𝐵𝐶2=10cm

根据折叠的性质可知：AE＝AB＝10cm

∵AC＝8cm

∴CE＝AE﹣AC＝2cm

即CE的长为2cm

故答案为：2．

总结提升：此题考查翻折问题 将图形进行折叠后 两个图形全等 是解决折叠问题的突破口．

3．（2020秋•金台区校级期末）如图 在△ABC中 ∠ACB＝90° 点E F在边AB上 将边AC沿CE翻折 使点A落在AB上的点D处 再将边BC沿CF翻折 使点B落在CD的延长线上的点B′处

（1）求∠ECF的度数；

第 1 页 共 12 页 八年级数学下册《第十七章-勾股定理》单元测试卷及答案(人教版)

一 选择题(每小题3分 共30分)

1. 如果下列各组数是三角形的三边长，那么不能组成直角三角形的一组数是( )

A. √2 √3 √5 B. 1.5

C. 32 42 52 D. 1 2

2. 点𝐴(−3,−4)到原点的距离为( )

A. 3 B. 4 C. 5 D. 7

3. 有一个直角三角形的两边长分别为3和4，则第三边的长为( )

A. 5 B. √7 C. √5 D. 5或√7

4．如果直角三角形两直角边的比为5∶12， 则斜边上的高与斜边的比为（ ）

A 60∶13 B 5∶12 C 12∶13 D 60∶169

5. 若一直角三角形两边长分别为12和5 则第三边长为（ ）

A．13 B．13或 C．13或15 D．15

6．一个圆桶底面直径为24cm ，高32cm，则桶内所能容下的最长木棒为（ ）

A．20cm B．50cm C．40cm D．45cm

7．如图 小明准备测量一段水渠的深度 他把一根竹竿AB竖直插到水底 此时竹竿AB离岸边点C处的距离米．竹竿高出水面的部分AD长0.5米 如果把竹竿的顶端A拉向岸边点C处 竿顶和岸边的水面刚好相齐 则水渠的深度BD为（ ）

A．2米 B．2.5米 C．2.25米 D．3米 1.5CD第 2 页 共 12 页 8.如图， “赵爽弦图”是用四个相同的直角三角形与一个小正方形无缝隙地铺成一个大正方形

已知大正方形面积为25 (𝑥+𝑦)2=49 用𝑥 𝑦表示直角三角形的两直角边(𝑥>𝑦) 下列选项中正确的是( )

A. 小正方形面积为4 B. 𝑥2+𝑦2=5

八年级数学下册第十七章《勾股定理》单元测试卷-人教版(含答案)

一、单选题（本大题共12小题，每小题3分，共36分)

1．如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“勾股方圆图”（又称赵爽弦图），它是由四个全等的直角三角形（直角边分别为a，b，斜边为c）与中间的一个小正方形拼成的一个大正方形．如果大正方形的面积为11，小正方形的面积为3，则44ab的值为（ ）

A．68 B．89 C．119 D．130

2．如图，ABC中，90,8,6ACBACBC，将ADE沿DE翻折，使点A与点B重合，则CE的长为（ ）

A．198 B．2 C．254 D．74

3．已知点M的坐标为3,4，则下列说法正确的是（ ）

A．点M在第二象限内 B．点M到x轴的距离为3

C．点M关于y轴对称的点的坐标为3,4 D．点M到原点的距离为5

4．如图，点A表示的实数是（ ）

A．﹣3 B．﹣5 C．﹣6 D．﹣7

5．如图，圆柱的底面周长为12cm，AB是底面圆的直径，在圆柱表面的高BC上有一点D，且10cmBC，2cmDC．一只蚂蚁从点A出发，沿着圆柱体的表面爬行到点D的最短路程是（ ）cm．

A．14 B．12 C．10 D．8

6．△ABC的三边长a，b，c满足5a+（b﹣12）2+|c﹣13|＝0，则△ABC的面积是（ ）

A．65 B．60 C．30 D．26

7．如图，RtABC中，90,4,6BABBC，将ABC折叠，使点C与AB的中点D重合，折痕交AC于点M，交BC于点N，则线段CN的长为（ ）.

A．73 B．83 C．3 D．103

8．如图，在ABC中，△B＝22.5°，△C＝45°，若AC＝2，则ABC的面积是（ ）

A．322 B．1+2 C．22 D．2+2 9．我们知道，如果直角三角形的三边的长都是正整数，这样的三个正整数就叫做一组勾股数．如果一个正整数c能表示为两个正整数a，b的平方和，即22cab，那么称a，b，c为一组广义勾股数，c为广义斜边数，则下面的结论：△m为正整数，则3m，4m，5m为一组勾股数；△1，2，3是一组广义勾股数；△13是广义斜边数；△两个广义斜边数的和是广义斜边数；△若2222,12,221akkbkckk，其中k为正整数，则a，b，c为一组勾股数；△两个广义斜边数的积是广义斜边数．依次正确的是（ ）

第十七章《勾股定理》单元检测题

一、选择题(每小题3分，共30分)

1．如图，以数轴的单位长度线段为边作一个正方形，以原点为圆心，正方形对角线长为半径画弧，交数轴于点A，则点A表示的数是（ ）

A．1 B．﹣1 C．1﹣ D．

2．如图，线段AB＝、CD＝，那么，线段EF的长度为（ ）

A． B． C． D．

3．下列说法：

①若a，b，c为一组勾股数，那么4a，4b，4c仍是勾股数；

②如果直角三角形的两边是3，4，那么斜边必是5；

③如果一个三角形的三边是12，25，21，那么此三角形必是直角三角形；

④一个等腰直角三角形的三边是a，b，c（a＞b＝c），那么a2：b2：c2＝2：1：1，

其中正确的是（ ）

A．①② B．①③ C．①④ D．②④

4．如图，在Rt△ABC中，∠BAC＝90°．ED是BC的垂直平分线，BD平分∠ABC，AD＝3．则CD的长为（ ）

A．6 B．5 C．4 D．3 5．如图：在△ABC中，CE平分∠ACB，CF平分∠ACD，且EF∥BC交AC于M，若CM＝5，则CE2+CF2等于（ ）

A．75 B．100 C．120 D．125

6．若ABC的三边长a、b、c满足222681050abcabc，那么ABC是（ ）

A．等腰三角形 B．直角三角形

C．锐角三角形 D．钝角三角形

7．已知一个直角三角形的两边长分别为1和2，则第三边长是（ ）

A．3 B．3 C．5 D．3或5

8．如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案．已知大正方形面积为49，小正方形面积为4，若用x，y表示直角三角形的两直角边（x＞y），下列结论：①x2+y2＝49；②x﹣y＝2；③2xy+4＝49．其中正确的结论是（ ）

A．①② B．② C．①②③ D．①③

9．如图，笑笑将一张A4纸（A4纸的尺寸为210mm×297mm，AC＞AB）剪去了一个角，量得CF＝90mm，BE＝137mm，则剪去的直角三角形的斜边长为（ ）

第17章 勾股定理

一．选择题（共10小题）

1．下列各组数是勾股数的是（ ）

A．2，3，4 B．0.3，0.4，0.5

C．7，24，25 D．，，

2．△ABC中，∠A，∠B，∠C所对的边分别为a，b，c，下列条件不能判断△ABC是直角三角形的是（ ）

A．a2+b2＝c2 B．a＝5，b＝12，c＝13

C．∠A：∠B：∠C═3：4：5 D．∠A＝∠B+∠C

3．如图，长方形ABCD中，AB＝3，AD＝1，AB在数轴上，若以点A为圆心，AC的长为半径作弧交数轴于点M，则点M表示的数为（ ）

A．﹣1 B．﹣1 C．2 D．

4．如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，若AC＝4，BC＝6，将四个直角三角形中边长为4的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是（ ）

A．56 B．24 C．64 D．32

5．如图，点E在正方形ABCD的边AB上，若EB＝1，EC＝2，那么正方形ABCD的面积为（ ）

A． B．3 C． D．5 6．勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内．若知道图中阴影部分的面积，则一定能求出（ ）

A．直角三角形的面积

B．最大正方形的面积

C．较小两个正方形重叠部分的面积

D．最大正方形与直角三角形的面积和

7．如图，今年第9号台风利奇马”过后，市体育中心附近一棵大树在高于地面3米处折断，大树顶部落在距离大树底部4米处的地面上，那么树高是（ ）

A．7m B．8m C．9m D．12m

8．将一根长为25厘米的筷子置于底面直径为5厘米，高为12厘米的圆柱形水杯中，设筷子露在杯子外的长为h厘米，则h的取值范围是（ ）

A．12≤h≤13 B．11≤h≤12 C．11≤h≤13 D．10≤h≤12