八年级数学下册《勾股定理》练习题与答案(人教版)

—————————— 唐玲制作仅供学习交流 ——————————

唐玲

初中数学试卷

勾股定理同步练习题

1．已知直角三角形中30°角所对的直角边长是32cm，则另一条直角边的长是（ ）

A. 4cm B. 34cm C. 6cm D. 36cm

2．△ABC中，AB＝15，AC＝13，高AD＝12，则△ABC的周长为（ ）

A．42 B．32 C．42 或 32 D．37 或 33

3．一架25分米长的梯子，斜立在一竖直的墙上，这时梯足距离墙底端7分米.如果梯子的顶端沿墙下滑4分米，那么梯足将滑动( )

A. 9分米 B. 15分米 C. 5分米 D. 8分米

4． 如图，学校有一块长方形花铺，有极少数人为了避开拐角走“捷径”，在花铺内走出了一条“路”．他们仅仅少走了

步路（假设2步为1米），却踩伤了花草．

5. 在△ABC中，∠C＝90°，（1）已知 a＝2.4，b＝3.2，则c＝ ；

（2）已知c＝17，b＝15，则△ABC面积等于 ；

（3）已知∠A＝45°，c＝18，则a＝ .

6. 一个矩形的抽斗长为24cm，宽为7cm,在里面放一根铁条，那么铁条最长可以是 ．

7. 在Rt△ABC中，∠C＝90°，BC＝12cm，S△ABC＝30cm2，则AB＝

.

8. 等腰△ABC的腰长AB＝10cm，底BC为16cm，则底边上的高为 ，面积为 .

9. 一个直角三角形的三边为三个连续偶数，则它的三边长分别为 ． “路”4m3m —————————— 唐玲制作仅供学习交流 ——————————

唐玲 10．一天，小明买了一张底面是边长为260cm的正方形，厚30cm的床垫回家．到了家门口，才发现门口只有242cm高，宽100cm．你认为小明能拿进屋吗？

初中数学试卷

金戈铁骑整理制作

人教版数学八年级下册 第十七章 勾股定理 利用勾股定理解决问题 专题练习题

1．如图，把长方形纸条ABCD沿EF，GH同时折叠，B，C两点恰好落在AD边的P点处，若∠FPH＝90°，PF＝8，PH＝6，则长方形ABCD的边BC的长为( )

A．20 B．22 C．24 D．30

2．如图，长方形纸片ABCD中，已知AD＝8，折叠纸片使AB边与对角线AC重合，点B落在点F处，折痕为AE，且EF＝3，则AB的长为( )

A．3 B．4 C．5 D．6

3．如图，在Rt△ABC中，AB＝9，BC＝6，∠B＝90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为(

)

A.53 B.52 C．4 D．5

4．如图，在三角形纸片ABC中，BC＝3，AB＝6，∠BCA＝90°.在AC上取一点E，以BE为折痕，使AB的一部分与BC重合，点A与BC延长线上的点D重合，则DE的长度为(

)

A．6 B．3 C．23 D.3

5．如图，把长方形纸片ABCD折叠，使点B恰好落在CD边的中点E处，折痕为AF.若CD＝6，则AF等于( ) A．43 B．33 C．42

D．8

6．如图①是一个直角三角形纸片，∠A＝30°，BC＝4 cm，将其折叠，使点C落在斜边上的点C′处，折痕为BD，如图②，再将②沿DE折叠，使点A落在DC′的延长线上的点A′处，如图③，则折痕DE的长为(

)

A.83 cm B．23 cm C．22 cm D．3 cm

7. 如图，正方形ABCD的边长为2，其面积标记为S1，以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S2……按照此规律继续下去，则S2018的值为( )

勾股定理同步练习题

1．已知直角三角形中30°角所对的直角边长是32cm，则另一条直角边的长是（ ）

A. 4cm B. 34cm C. 6cm D. 36cm

2．△ABC中，AB＝15，AC＝13，高AD＝12，则△ABC的周长为（ ）

A．42 B．32 C．42 或 32 D．37 或 33

3．一架25分米长的梯子，斜立在一竖直的墙上，这时梯足距离墙底端7分米.如果梯子的顶端沿墙下滑4分米，那么梯足将滑动( )

A. 9分米 B. 15分米 C. 5分米 D. 8分米

4． 如图，学校有一块长方形花铺，有极少数人为了避开拐角走“捷径”，在花铺内走出了一条“路”．他们仅仅少走了

步路（假设2步为1米），却踩伤了花草．

5. 在△ABC中，∠C＝90°，（1）已知 a＝2.4，b＝3.2，则c＝ ；

（2）已知c＝17，b＝15，则△ABC面积等于 ；

（3）已知∠A＝45°，c＝18，则a＝ .

6. 一个矩形的抽斗长为24cm，宽为7cm,在里面放一根铁条，那么铁条最长可以是 ．

7. 在Rt△ABC中，∠C＝90°，BC＝12cm，S△ABC＝30cm2，则AB＝

.

8. 等腰△ABC的腰长AB＝10cm，底BC为16cm，则底边上的高为 ，面积为 .

9. 一个直角三角形的三边为三个连续偶数，则它的三边长分别为 ．

10．一天，小明买了一张底面是边长为260cm的正方形，厚30cm的床垫回家．到了家门口，才发现门口只有242cm高，宽100cm．你认为小明能拿进屋吗？ ．

“路”4m3m

17.1勾股定理 应用题 练习题

1．如图，一圆柱高8cm，底面半径为 cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程是（ ）

A．6cm B．8cm C．10cm D．12cm

2．如图，一只蚂蚁从长、宽都是4，高是6的长方体纸箱的A点沿纸箱爬到B点，那么它所行的最短路线的长是（ ）

A．9 B．10 C． D．

3．如图，长为8cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升3cm至D点，则橡皮筋被拉长了（ ）

A．2cm B．3cm C．4cm D．5cm

4．一艘轮船以16海里∕小时的速度从港口A出发向东北方向航行，同时另一轮船以12海里∕小时从港口A出发向东南方向航行，离开港口3小时后，则两船相距（ ）

A．36海里 B．48海里 C．60海里 D．84海里

5．如图，在6个边长为1的小正方形及其部分对角线构成的图形中，如图从A点到B点只能沿图中的线段走，那么从A点到B点的最短距离的走法共有（ ）

A．1种 B．2种 C．3种 D．4种

6．小明准备测量一段河水的深度，他把一根竹竿竖直插到离岸边1.5m远的水底，竹竿高出水面0.5m，把竹竿的顶端拉向岸边，竿顶和岸边的水面刚好相齐，则河水的深度为（ ）

A．2m B．2.5m C．2.25m D．3m

7．有一块边长为24米的正方形绿地，如图所示，在绿地旁边B处有健身器材，由于居住在A处的居民践踏了绿地，小明想在A处树立一个标牌“少走▇米，踏之何忍”请你计算后帮小明在标牌的“▇”填上适当的数字是（ ）

第1页—总14页 《勾股定理》典型例题分析

考点一：利用勾股定理求面积

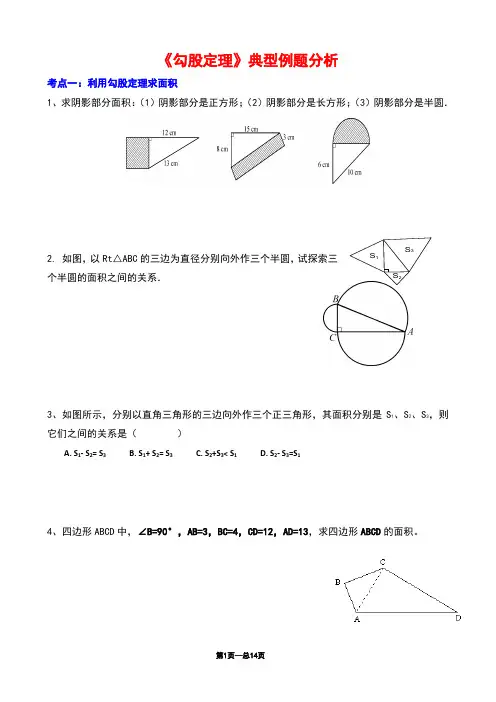
1、求阴影部分面积：（1）阴影部分是正方形；（2）阴影部分是长方形；（3）阴影部分是半圆．

2. 如图，以Rt△ABC的三边为直径分别向外作三个半圆，试探索三个半圆的面积之间的关系．

3、如图所示，分别以直角三角形的三边向外作三个正三角形，其面积分别是S1、S2、S3，则它们之间的关系是（ ）

A. S1- S2= S3 B. S1+ S2= S3 C. S2+S3< S1 D. S2- S3=S1

4、四边形ABCD中，∠B=90°，AB=3，BC=4，CD=12，AD=13，求四边形ABCD的面积。

S3S2S1

第2页—总14页 考点二：在直角三角形中，已知两边求第三边

1．在直角三角形中,若两直角边的长分别为1cm，2cm ，则斜边长为 ．

2．已知直角三角形的两边长为3、2，则另一条边长的平方是

3、已知直角三角形两直角边长分别为5和12， 求斜边上的高．

4、把直角三角形的两条直角边同时扩大到原来的2倍，则斜边扩大到原来的（ ）

A． 2倍 B． 4倍 C． 6倍 D． 8倍

5、在Rt△ABC中，∠C=90°

①若a=5，b=12，则c=___________；

②若a=15，c=25，则b=___________；

③若c=61，b=60，则a=__________；

④若a∶b=3∶4，c=10则Rt△ABC的面积是=________。

6、如果直角三角形的两直角边长分别为1n2，2n（n>1），那么它的斜边长是（ ）

A、2n B、n+1 C、n2－1 D、1n2

7、在Rt△ABC中，a,b,c为三边长，则下列关系中正确的是（ ）

17.1 勾股定理

一、单选题

1．若直角三角形两直角边长分别为5和12，则斜边的长为（ ）

A．17 B．7 C．14 D．13

2．已知直角三角形两边的长为3和4，则此三角形的周长为（ ）

A．12 B．7+7 C．12或7+7 D．以上都不对

3．如图，正方形的一个顶点为A，有两个顶点对应于数轴上表示1和2的两点，以原点O为圆心，以OA为半径顺时针画弧，交数轴于点B，则点B对应的数是（ ）

A．3 B．5 C．6 D．7

4．在△ABC中，AB=15，AC=13，BC上的高AD长为12，则△ABC的面积为（ ）

A．84 B．24 C．24或84 D．42或84

5．以直角三角形a、b、c为边，向外作半圆，等腰直角三角形和正方形，上述四种情况的面积关系满足S1+S2＝S3图形个数有（ ）

A．3 B．2 C．1 D．0

6．如图，在22的方格中，小正方形的边长是1，点A、B、C都在格点上，则AC边上的高为（ ）

A．5 B．322 C．355 D．32

7．如图，一个长为10米的梯子斜靠在墙上，梯子的顶端距地面的垂直距离为8米，如果梯子的顶端下滑1米，那么梯子的底端的滑动距离（ ）

A．等于1米 B．大于1米 C．小于1米 D．不能确定

8．如图，盒内长、宽、高分别是6cm、3cm、2cm，盒内可放木棒最长的长度是（ ）

A．6cm B．7cm C．8cm D．9cm

9．如图，高速公路上有A、B两点相距25km，C、D为两村庄，已知DA＝10km，CB＝15km．DA△AB于A，CB△AB于B，现要在AB上建一个服务站E，使得C、D两村庄到E站的距离相等，则AE的长是（ ）km．

A．5 B．10 C．15 D．25

10．如图：有一圆柱，它的高等于8cm，底面直径等于4cm（π=3），在圆柱下底面的A点有一只蚂蚁，它想吃到上底面与A相对的B点处的食物，需要爬行的最短路程大约（ ）

依提木孔乡中学 买买提依力·吾司曼

《勾股定理》练习题

一、选择题（12×3′=36′）

1．已知一个Rt△的两边长分别为3和4，则第三边长的平方是（ ）

A、25 B、14 C、7 D、7或25

2．下列各组数中，以a，b，c为边的三角形不是Rt△的是（ ）

A、a=1.5，b=2,c=3 B、a=7,b=24,c=25

C、a=6,b=8,c=10 D、a=3,b=4,c=5

3．若线段a，b，c组成Rt△，则它们的比为（ ）

A、2∶3∶4 B、3∶4∶6 C、5∶12∶13 D、4∶6∶7

4．Rt△一直角边的长为11，另两边为自然数，则Rt△的周长为（ ）

A、121 B、120 C、132 D、不能确定

5．如果Rt△两直角边的比为5∶12，则斜边上的高与斜边的比为（ ）

A、60∶13 B、5∶12 C、12∶13 D、60∶169

6．如果Rt△的两直角边长分别为n2－1，2n（n>1），那么它的斜边长是（ ）

A、2n B、n+1 C、n2－1 D、n2+1

7．已知Rt△ABC中，∠C=90°，若a+b=14cm，c=10cm，则Rt△ABC的面积是（ ）

A、24cm2 B、36cm2 C、48cm2 D、60cm2

8．等腰三角形底边上的高为8，周长为32，则三角形的面积为（ ）

A、56 B、48 C、40 D、32

9．三角形的三边长为（a+b）2=c2+2ab,则这个三角形是( )

A. 等边三角形; B. 钝角三角形; C. 直角三角形; D. 锐角三角形.

10．某市在旧城改造中，计划在市内一块如图所示的三角形空地上种植草皮以美化环境，已知这种草皮每平方米售价a元，则购买这种草皮至少需要（ ）

人教版初中八年级数学勾股定理解答题练习含答案

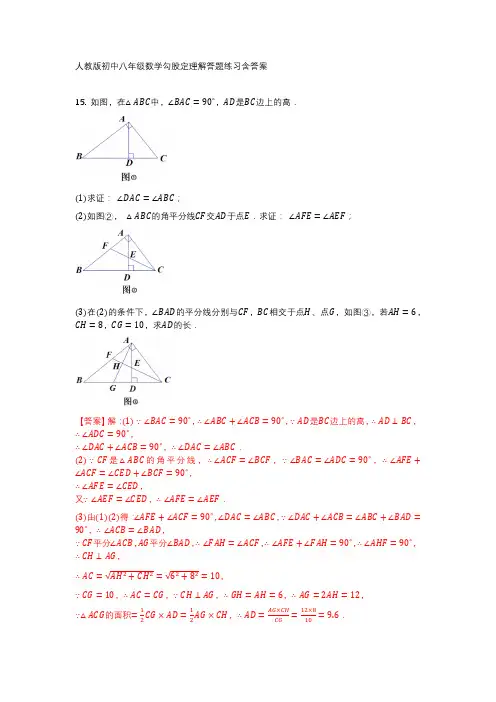
15. 如图，在△𝐴𝐵𝐶中，∠𝐵𝐴𝐶=90∘，𝐴𝐷是𝐵𝐶边上的高．

(1)求证： ∠𝐷𝐴𝐶=∠𝐴𝐵𝐶；

(2)如图②， △𝐴𝐵𝐶的角平分线𝐶𝐹交𝐴𝐷于点𝐸．求证： ∠𝐴𝐹𝐸=∠𝐴𝐸𝐹；

(3)在(2)的条件下，∠𝐵𝐴𝐷的平分线分别与𝐶𝐹，𝐵𝐶相交于点𝐻、点𝐺，如图③，若𝐴𝐻=6，𝐶𝐻=8，𝐶𝐺=10，求𝐴𝐷的长．

【答案】解：(1)∵∠𝐵𝐴𝐶=90∘，∴∠𝐴𝐵𝐶+∠𝐴𝐶𝐵=90∘，∵𝐴𝐷是𝐵𝐶边上的高，∴𝐴𝐷⊥𝐵𝐶，∴∠𝐴𝐷𝐶=90∘，

∴∠𝐷𝐴𝐶+∠𝐴𝐶𝐵=90∘，∴∠𝐷𝐴𝐶=∠𝐴𝐵𝐶．

(2)∵𝐶𝐹是△𝐴𝐵𝐶的角平分线，∴∠𝐴𝐶𝐹=∠𝐵𝐶𝐹，∵∠𝐵𝐴𝐶=∠𝐴𝐷𝐶=90∘，∴∠𝐴𝐹𝐸+∠𝐴𝐶𝐹=∠𝐶𝐸𝐷+∠𝐵𝐶𝐹=90∘，

∴∠𝐴𝐹𝐸=∠𝐶𝐸𝐷，

又∵∠𝐴𝐸𝐹=∠𝐶𝐸𝐷，∴∠𝐴𝐹𝐸=∠𝐴𝐸𝐹．

(3)由(1)(2)得：∠𝐴𝐹𝐸+∠𝐴𝐶𝐹=90∘，∠𝐷𝐴𝐶=∠𝐴𝐵𝐶，∵∠𝐷𝐴𝐶+∠𝐴𝐶𝐵=∠𝐴𝐵𝐶+∠𝐵𝐴𝐷=90∘，∴∠𝐴𝐶𝐵=∠𝐵𝐴𝐷，

∵𝐶𝐹平分∠𝐴𝐶𝐵，𝐴𝐺平分∠𝐵𝐴𝐷，∴∠𝐹𝐴𝐻=∠𝐴𝐶𝐹，∴∠𝐴𝐹𝐸+∠𝐹𝐴𝐻=90∘，∴∠𝐴𝐻𝐹=90∘，∴𝐶𝐻⊥𝐴𝐺，

∴𝐴𝐶=√𝐴𝐻2+𝐶𝐻2=√62+82=10，

∵𝐶𝐺=10，∴𝐴𝐶=𝐶𝐺，∵𝐶𝐻⊥𝐴𝐺，∴𝐺𝐻=𝐴𝐻=6，∴𝐴𝐺=2𝐴𝐻=12，

∵△𝐴𝐶𝐺的面积=12𝐶𝐺×𝐴𝐷=12𝐴𝐺×𝐶𝐻，∴𝐴𝐷=𝐴𝐺×𝐶𝐻𝐶𝐺=12×810=9.6．

17.1勾股定理 同步练习

基础题

一、填空题

1．在△ABC中，若∠A＋∠B＝90°，AC＝5，BC＝3，则AB＝______，AB边上的高CE＝______．

2．在△ABC中，若AB＝AC＝20，BC＝24，则BC边上的高AD＝______，AC边上的高BE＝______．

3．在△ABC中，若AC＝BC，∠ACB＝90°，AB＝10，则AC＝______，AB边上的高CD＝______．

4．在△ABC中，若AB＝BC＝CA＝a，则△ABC的面积为______．

5．在△ABC中，若∠ACB＝120°，AC＝BC，AB边上的高CD＝3，则AC＝______，AB＝______，BC边上的高AE＝______．

二、选择题

6．已知直角三角形的周长为，斜边为2，则该三角形的面积是( )．

(A) (B) (C) (D)1

7．若等腰三角形两边长分别为4和6，则底边上的高等于( )．

(A) (B)或 (C) (D)或

三、解答题

8．如图，在Rt△ABC中，∠C＝90°，D、E分别为BC和AC的中点，AD＝5，BE＝求AB的长．

9．在数轴上画出表示及的点．

提高题

10．如图，△ABC中，∠A＝90°，AC＝20，AB＝10，延长AB到D，使CD＋DB＝624143217741242471021013AC＋AB，求BD的长．

11．如图，将矩形ABCD沿EF折叠，使点D与点B重合，已知AB＝3，AD＝9，求BE的长．

12．如图，折叠矩形的一边AD，使点D落在BC边的点F处，已知AB＝8cm，BC＝10cm，求EC的长．

13．已知：如图，△ABC中，∠C＝90°，D为AB的中点，E、F分别在AC、BC上，且DE⊥DF．求证：AE2＋BF2＝EF2．

拓展题

14．如图，已知△ABC中，∠ABC＝90°，AB＝BC，三角形的顶点在相互平行的三条直线l1，l2，l3上，且l1，l2之间的距离为2，l2，l3之间的距离为3，求AC的长是多少?

- 1 -

人教版 八年级数学下册 勾股定理的应用（分课时练习）

课后练习（一）

主讲教师：傲德

班级 姓名

题一：如图，矩形ABCD的对角线AC=10，BC=8，则图中五个小矩形的周长之和为（ ）

A．14 B．16 C．20 D．28

题二：勾股定理是几何中的一个重要定理．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，∠BAC=90°，AB=3，AC=4，点D，E，F，G，H，I都在矩形KLMJ的边上，则矩形KLMJ的面积为（ ）

A．90 B．100 C．110 D．121

题三：如图，在一块形状为直角梯形的草坪中，修建了一条由A→M→N→C的小路（M、N分别是AB、CD中点）．极少数同学为了走“捷径”，沿线段AC行走，破坏了草坪，实际上他们仅少走了

．

题四：在长，宽，高分别为12cm，4cm，3cm的木箱中，放一根木棒，能放进去的木棒的最大长度为

cm．

题五：如图，Rt△ABC中，AC=5，BC=12，分别以它的三边为直径向上作三个半圆，则阴影部分面积为 ．

- 2 -

题六：一个长为10m的梯子斜靠在墙上，梯子底端距墙底6m．

（1）若梯子的底端水平向外滑动1m，梯子的顶端下滑多少米？

（2）如果梯子顶端向下滑动的距离等于底端向外滑动的距离，那么滑动的距离是多少米？

题七：等腰直角△ABC中，BC=AC=1，以斜边AB和长度为1的边BB1为直角边构造直角△ABB1，如图，这样构造下去…，则AB3= ；ABn= ．

课后练习（二）

主讲教师：傲德

题一：如图为梯形纸片ABCD，E点在BC上，且∠AEC＝∠C＝∠D＝90°，AD＝3，BC＝9，CD＝8．若以AE为折线，将点C折至BE上，使得CD与AB交于F点，则BF长度为（ ）

1 勾股定理 练习题

1.已知x=3－2,那么x+x1的值等于( )

A.23 B.－23 C.22 D.－22

2.已知a－b=23－1,ab=3,则(a+1)(b－1)的值为( )

A.－3 B.33 C.22 D.－22

3.当a<0,b<0时，baba2-可变形为（ ）

A. 2)(ba B. 2)-(-ba C.2)--(ba D. 2)---(ba

4.已知a、b、c为△ABC三边，且满足0))((22222cbaba，则它的形状为（ ）

A.直角三角形 B.等腰三角形 C.等腰直角三角形 D.等腰三角形或直角三角形

5.如果最简二次根式83a与a217是同类根式(最简形式被开方数相同的二次根式),那么使xa24有意义的x的取值范围是( )

A.x≤10 B.x≥10 C.x<10 D.x>10

6.直角三角形的面积为S，斜边上的中线长为d，则这个三角形周长为（ ）

A.dSd22 B.dSd--2 C.dSd222 D.dSd22

7.如图①，矩形ABCD，AB=12cm，AD=16cm，现将其按下列步骤折叠：

（1）将边AB向AD折去，使AB落在AD上，得到折痕AF，如图②

（2）将△AFB沿BF折叠，AF与DC交点G，如图③

则所得梯形BDGF的周长等于（ ）

A.12+22 B.24+22 C.24+42 D.12+42

第17章 勾股定理

一．选择题（共10小题）

1．已知Rt△ABC的三边分别为a、b、c，则下列结论不可能成立的是（ ）

A．a2﹣b2＝c2 B．∠A﹣∠B＝∠C

C．∠A：∠B：∠C＝3：4：5 D．a：b：c＝7：24：25

2．有一个面积为1的正方形，经过一次“生长”后，在他的左右肩上生出两个小正方形，其中，三个正方形围成的三角形是直角三角形，再经过一次“生长”后，变成了下图，如果继续“生长”下去，它将变得“枝繁叶茂”，请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是（ ）

A．1 B．2018 C．2019 D．2020

3．如图，网格中每个小正方形的边长均为1，点A，B，C都在格点上，以A为圆心，AB为半径画弧，交最上方的网格线于点D，则CD的长为（ ）

A． B．0.8 C．3﹣ D．

4．如图△ABC中，∠D＝90°，C是BD上一点，已知CB＝9，AB＝17，AD＝8，则DC的长是（ ）

A．8 B．9 C．6 D．15

5．下列说法中，正确的个数有（ ）

①已知直角三角形的面积为2，两直角边的比为1：2，则斜边长为；

②直角三角形的最大边长为，最短边长为1，则另一边长为；

③在△ABC中，若∠A：∠B：∠C＝1：5：6，则△ABC为直角三角形；

④等腰三角形面积为12，底边上的高为4，则腰长为5．

A．1个 B．2个 C．3个 D．4个

6．我国是最早了解勾股定理的国家之一．下面四幅图中，不能证明勾股定理的是（

）

A． B．

C． D．

7．如图，四边形ABCD中，∠ABC＝90°，AC＝BD，AC⊥BD，若AB＝4，AD＝5，则DC的长（

）

A．7 B． C． D．2

8．如图，某公司举行周年庆典，准备在门口长25米，高7米的台阶上铺设红地毯，已知台阶的宽为3米，则共需购买（ ）m2的红地毯．

A．21 B．75 C．93 D．96

2022-2023学年人教版八年级数学下册《17.1勾股定理》同步练习题（附答案）

一．选择题

1．已知直角三角形的两条边长分别是3和4，那么这个三角形的第三条边的长为（ ）

A．5 B．25 C． D．5或

2．△ABC中，AB＝20，AC＝13，高AD＝12，则△ABC的面积为（ ）

A．66 B．126 C．54或44 D．126或66

3．如图，Rt△ABC中，∠BAC＝90°，分别以边AB，CA，BC向外作正方形，正方形ABIH的面积为25，正方形BDEC的面积为169，则正方形ACFG的面积是（ ）

A．194 B．144 C．122 D．110

4．下面图形能够验证勾股定理的有（ ）

A．4个 B．3个 C．2个 D．1个

5．如图，我国古代的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形，若小正方形的面积为1，大正方形的面积为13，则直角三角形较短的直角边a与较长的直角边b的比的值是（ ）

A． B． C． D． 6．如图是一正方体的平面展开图，若AB＝6，则该正方体A、B两点间的距离为（ ）

A．2 B．3 C．4 D．6

7．如图，在△ABC中，∠C＝90°，分别以A、B为圆心画弧，所画的弧交于两点，再连接该两点所在直线交BC于点D，连接AD．若BD＝2，则AD的长为（ ）

A． B． C．1 D．2

8．如图，是我国古代著名的“赵爽弦图”的示意图，此图是由四个全等的直角三角形拼接而成，其中AE＝10，BE＝24，则EF的长是（ ）

A．14 B．13 C．14 D．14

9．如图，正方形ABCD的面积为15，Rt△BCE的斜边CE的长为8，则BE的长为（ ）

A．17 B．10 C．6 D．7

10．如图，在4×4的正方形网格中，所有线段的端点都在格点处，则这些线段的长度是无理数的有（ ）

A．1条 B．2条 C．3条 D．4条 二．填空题

人教版八年级下册数学第十七章 勾股定理含答案

一、单选题(共15题，共计45分)

1、在 中，∠C=90°，sinA= ，则tanA=（ ） A. B. C.1 D.

2、如图，正方形ABCD的边长为4，点E在对角线BD上，且∠BAE=22.5°，EF⊥AB，垂足为F，则EF的长为（ ）

A.1 B. C. D.

3、如图，在梯形ABCD中，AB∥CD，∠D=90°，AD＝CD＝4，AB=1，F为AD的中点，则F到BC的距离是（ ）．

A.1 B.2 C.4 D.8

4、直角三角形中一直角边的长为9，另两边为连续自然数，则直角三角形的周长为（ ）

A.90 B.120 C.121 D.不能确定

5、如图，在Rt△ABC中，∠ACB=90°，BD平分∠ABC．若CD=3，BC+AB=16，则△ABC的面积为（ ）

A.16 B.18 C.24 D.32

6、在平面直角坐标系中,点A,B的坐标分别为(－6,0),(0,8). 以点A为圆心,以AB长为半径画弧交x轴于点C,则点C的坐标为（ ）.

A.(6,0) B.(4,0) C.(6,0)或(-16,0) D.(4,0)或(-16,0)

7、如图，平面直角坐标系中，A点坐标为 ，点 在直线

上运动，设 的值为 ，则下面能够大致反映w与m的函数关系的图象是（ ）

A. B. C.

D.

8、如图，已知由16个边长为1的小正方形拼成的图案中，有五条线段PA、PB、PC、PD、PE，其中长度是有理数的有 （ ）

A.1条 B.2条 C.3条 D.4条

9、在直角三角形ABC中，斜边AB=1，则AB²+BC²+AC²=（ ）

A.2 B.4 C.6 D.8

10、如图，在4×4的正方形方格图形中，小正方形的顶点称为格点，△ABC的顶点都在格点上，则图中∠ABC的余弦值是（ ）

第 1 页 共 20 页 人教版八年级数学下册《利用勾股定理解决折叠问题的技巧》练习题(附带答案）

类型一 利用勾股定理解决三角形的折叠问题

1．如图 △ABC中 ∠ACB＝90° AC＝8 BC＝6 将△ADE沿DE翻折

使点A与点B重合 则CE的长为 ．

思路引领：设CE＝x 则AE＝BE＝8﹣x 在Rt△BCE中 由勾股定理可得62+x2＝（8﹣x）2 即可解得答案．

解：设CE＝x 则AE＝BE＝8﹣x

在Rt△BCE中 BC2+CE2＝BE2

∴62+x2＝（8﹣x）2

解得x=74

故答案为：74．

总结提升：本题考查直角三角形中的折叠问题 解题的关键是掌握折叠的性质 熟练应用勾股定理列方程解决问题．

2．（2021秋•介休市期中）如图所示 有一块直角三角形纸片 ∠C＝90° AC＝8cm BC＝6cm 将斜边AB翻折 使点B落在直角边AC的延长线上的点E处 折痕为AD 则CE的长为 cm．

思路引领：根据勾股定理可将斜边AB的长求出 根据折叠的性质知 AE＝AB 已知AC的长 可将CE的长求出．

解：在Rt△ABC中 第 2 页 共 20 页 ∵∠C＝90° AC＝8cm BC＝6cm

∴AB=√𝐴𝐶2+𝐵𝐶2=10cm

根据折叠的性质可知：AE＝AB＝10cm

∵AC＝8cm

∴CE＝AE﹣AC＝2cm

即CE的长为2cm

故答案为：2．

总结提升：此题考查翻折问题 将图形进行折叠后 两个图形全等 是解决折叠问题的突破口．

3．（2020秋•金台区校级期末）如图 在△ABC中 ∠ACB＝90° 点E F在边AB上 将边AC沿CE翻折 使点A落在AB上的点D处 再将边BC沿CF翻折 使点B落在CD的延长线上的点B′处

（1）求∠ECF的度数；

第 1 页 共 12 页 八年级数学下册《第十七章-勾股定理》单元测试卷及答案(人教版)

一 选择题(每小题3分 共30分)

1. 如果下列各组数是三角形的三边长，那么不能组成直角三角形的一组数是( )

A. √2 √3 √5 B. 1.5

C. 32 42 52 D. 1 2

2. 点𝐴(−3,−4)到原点的距离为( )

A. 3 B. 4 C. 5 D. 7

3. 有一个直角三角形的两边长分别为3和4，则第三边的长为( )

A. 5 B. √7 C. √5 D. 5或√7

4．如果直角三角形两直角边的比为5∶12， 则斜边上的高与斜边的比为（ ）

A 60∶13 B 5∶12 C 12∶13 D 60∶169

5. 若一直角三角形两边长分别为12和5 则第三边长为（ ）

A．13 B．13或 C．13或15 D．15

6．一个圆桶底面直径为24cm ，高32cm，则桶内所能容下的最长木棒为（ ）

A．20cm B．50cm C．40cm D．45cm

7．如图 小明准备测量一段水渠的深度 他把一根竹竿AB竖直插到水底 此时竹竿AB离岸边点C处的距离米．竹竿高出水面的部分AD长0.5米 如果把竹竿的顶端A拉向岸边点C处 竿顶和岸边的水面刚好相齐 则水渠的深度BD为（ ）

A．2米 B．2.5米 C．2.25米 D．3米 1.5CD第 2 页 共 12 页 8.如图， “赵爽弦图”是用四个相同的直角三角形与一个小正方形无缝隙地铺成一个大正方形

已知大正方形面积为25 (𝑥+𝑦)2=49 用𝑥 𝑦表示直角三角形的两直角边(𝑥>𝑦) 下列选项中正确的是( )

A. 小正方形面积为4 B. 𝑥2+𝑦2=5