- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
故 α j 可由 α1,⋯,αr 线性表示。 T等 于 ' 价 。 T
9
3、最大线性无关组的求法 、 定理2 定理 矩阵的初等行变换不改变矩阵的列向量组的
线性相关性。 线性相关性。 定理2给出了求向量组的最大无关组的一个非常有 定理 给出了求向量组的最大无关组的一个非常有 用的方法。 用的方法。
10
8
性质2 性质2 证明
任何向量组与自己的最大无关组等价.
T : α1,⋯,αr ,⋯,αm T' : α1,⋯,αr ① T' 可由 T 线性表示 αi 用 α1,⋯,αr ,⋯,αm 线性表示,αi 前面系数取1,
其余向量前面系数取0 ②
T 可由 T' 线性表示
, 当 j = 1 2,⋯, r 时, α j可由 α1,⋯ αr 表示 , 当 j = r +1⋯, m时,α1,⋯,αr ,α j 线性相关, ,
11 − 9 5 9 0 0
T β3
2 3 1 3 0 0
T β4
2 1 α4 = α1 + α2 3 3
14
作业 P178 1 2(1)3
15
解 1
β1 β2 β3 β4
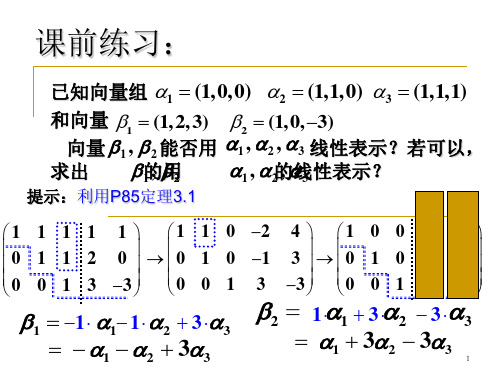
例3
求
α1 = (1,2,1,3)
α3 = (1,−3,−4,−7), α4 = (2,1,) ,
的一个最大无关组。 的一个最大无关组。 最大无关组 并把剩余向量用最大组表示。 并把剩余向量用最大组表示。 Θ Θ ΘΘ ΘΘ Θ Θ Θ Θ Θ 解
3 2 0 −2 = 即 −1 1 3 −1
1 0 2 −1 ⋮ −5 4 ⋮ 6 − 4 0 1 − 3 2 → ⋮ −5 3 0 0 0 0 ⋮ 9 −5 0 0 0 β2 = −α1 + 2α2 0
2 1 (α1,α2 ) = ( β1, β2 ) 3 2
第三节
向量组的秩
一、两个向量组的等价 二、极大无关组与向量组的秩
第三章
三、向量组的秩与矩阵秩的关系
1
一、向量组的等价 定义1 定义1 设有两个n 设有两个n元向量组
, (A): α1, α2 ,⋯ αr;
, (B): β1 , β2 ,⋯ βs。
如果( )中的每个向量均可用( ) 如果(A)中的每个向量均可用(B)中的向量线性 表示, 表示, 则称向量组(A)可用向量组(B)线性表示; 则称向量组(A)可用向量组(B)线性表示; 如果向量组( ) 与向量组( ) 如果向量组(A) 与向量组(B)能相互线性表示 (A)与(B)等价. 与 )等价. 则称向量组
α1 α2 α3 α4
1 1
1 1 0 0 1 2 3 4 5 0 1 0 − 3 A= → = B r( A) = 3 4 9 16 25 0 0 1 3 7 13 21 31 0 0 0 0 β1, β2 , β3 最大无关组,α1,α2 ,α3 为一个最大无关组。 β4 = β1 − 3β2 + 3β3 α4 = α1 − 3α2 + 3α3 13
线性相关, 线性无关, 首先 a1 , a2 线性无关, 又 a1 , a2 , a3 线性相关, 组成的部分组是极大无关组 所以 a1 , a2 组成的部分组是极大无关组 . 故此向量组的秩为 故此向量组的秩为 2 . 也是一个极大无关组 还可以验证 a2 , a3 也是一个极大无关组 . 唯一, 可看出 : r 唯一,但极大无关组一般情况下不唯一 . 注: r 是 A 中线性无关的向量个数的最大者 .
5
注: (1) 只含零向量的向量组没有极大无关组, 只含零向量的向量组没有极大无关组, 因此, 因此,零向量组的秩是零 . (2) 一个线性无关向量组的极大无关组就是其本身 一个线性无关向量组的极大无关组就是其本身. (3) 一个向量组的任一向量都能由它的极大无关组 线性表出 .
6
2 4 2 −1 −2 −1 例如: 例如:向量组 a1 = , a2 = , a3 = 3 5 4 1 4 −1
定理3(三秩相等) 三秩相等) 定理 三秩相等 秩 ( A) = A的列向量组的秩 = A行向量组的秩 由三秩相等定理知, 由三秩相等定理知 有限向量组的秩就是其排成 的矩阵的秩。 ,前面定理中出现的矩阵的秩又可 因此, 的矩阵的秩。 因此 看成向量组的秩。 看成向量组的秩。
11
对于给定的向量组, 对于给定的向量组,我们利用矩阵来求它的秩和 极大无关组, 极大无关组,具体步骤为 (1) 向量组 a1 , a2 , … , as ,作列向量构成矩阵 A . 作列向量构成矩阵 (2)
阶梯形矩阵) A B (阶梯形矩阵) →
初等行变换
a1 , a2 , … ,as 的秩 = R ( A ) = B 的非零行的行数 (3) 求出 B 的列向量组的极大无关组 ; (4) A 中与 B 的列向量组的极大无关组相对应部分的 的列向量的极大无关组, 列向量组即为 A 的列向量的极大无关组,即为 a1 , a2 , … ,as 的极大无关组 .
β1 = 2α1 − 3α2
2 −1 ( β1, β2 ) = (α1,α2 ) −3 2
故等价。 故等价。
4
二、最大线性无关组,向量组的秩 第一节中讨论向量组的线性相关性的时候, 第一节中讨论向量组的线性相关性的时候,矩阵 的秩起到十分重要的作用,为使讨论进一步深入, 的秩起到十分重要的作用,为使讨论进一步深入,下 面把秩的概念引入向量组中 . 设有向量组 如果有a 定义 2 设有向量组 A,如果有a1, … , ar ∈A,且有 (1) a1, a2 , … , ar 线性无关 ; (2) 向量组 A 中任意 r + 1 个向量(如果有的话 线性相关, 个向量 如果有的话)线性相关, 如果有的话 线性相关 则称 r 是向量组 A 的秩,a1, a2 , … , ar 为 A 的一个 极大无关组 .
7
性质1 性质
如果向量组的秩是 r ,则该向量组任 r 个线性 则该向量组任
无关的向量都可以作为最大线性无关组。 无关的向量都可以作为最大线性无关组。 性质2 性质2 任何向量组与自己的最大无关组等价. 任何向量组与自己的最大无关组等价.
性质3 如果向量组( )可由向量组( )线性表示, 性质3 如果向量组(A)可由向量组(B)线性表示, 则 R( A) ≤ R(B). 性质4 性质4 (A)与(B)组等价, 则 R( A) = R(B). ) )组等价,
12
1 1 1 例2 求 1 3 4 5 2 α1 = 4 , α2 = , α3 = , α4 = 9 16 25 7 13 21 31 的一个最大无关组及向量组的秩, 的一个最大无关组及向量组的秩, 并把剩余向量用 最大无关组线性表示。 最大无关组线性表示。 性表示
α α
T 1
T 2
α
T 3
α
T 4
1 4 1 2 2 −1 −3 1 1 −5 −4 −1 3 −6 −7 0
α1,α2 是最大无关组,
11 5 且 α3 = − α1 + α2 9 9
1 → 0 0 0
T β1T β2
0 1 0 0
2
2 3 −5 4 例 设 0 6 −2 − 4 1 ,β1 = ,α2 = α1 = ,β2 = , −1 1 −5 3 − 5 3 9 −1 3 ⋮ −5 4 证明 α1,α2与 β1, β2 等价。 2 等价。 0 − 2 ⋮ 6 − 4 证 C = (α1,α2 ⋮β1, β2 )= −1 1 ⋮ −5 3 3 −1 ⋮ 9 −5 1 0 2 −1 0 1 − 3 2 → 0 0 0 0 0 0 0 0 3