当前位置：文档之家 › 向量组的秩-例题选讲

向量组的秩-例题选讲

  • 格式：ppt
  • 大小：646.00 KB
  • 文档页数：36

下载文档原格式

  / 36

合集下载

求向量组的秩与极大无关组(修改整理)

求向量组的秩与极大无关组(修改整理)

求向量组的秩与最大无关组一、对于具体给出的向量组，求秩与最大无关组1、求向量组的秩（即矩阵的秩）的方法：为阶梯形矩阵【定理】矩阵的行秩等于其列秩，且等于矩阵的秩.(三秩相等)①把向量组的向量作为矩阵的列（或行）向量组成矩阵A；②对矩阵A进行初等行变换化为阶梯形矩阵B；③阶梯形B中非零行的个数即为所求向量组的秩．【例1】求下列向量组a１=(1, 2, 3, 4)，a2 =( 2, 3, 4, 5)，a3 =(3, 4, 5, 6)的秩. 解1：以a１,a２,a３为列向量作成矩阵A，用初等行变换将A化为阶梯形矩阵后可求.因为阶梯形矩阵的列秩为2，所以向量组的秩为2．解2：以a１,a２,a３为行向量作成矩阵A，用初等行变换将A化为阶梯形矩阵后可求.因为阶梯形矩阵的行秩为2，所以向量组的秩为2．2、求向量组的最大线性无关组的方法方法1 逐个选录法给定一个非零向量组A：α1, α2,…, αn①设α1≠ 0，则α1线性相关，保留α1②加入α2，若α2与α1线性相关，去掉α2；若α2与α1线性无关，保留α1，α2；③依次进行下去，最后求出的向量组就是所求的最大无关组【例2】求向量组：()()()1231,2,12,3,14,1,1,,,T T Tααα=-=-=-的最大无关组 解：因为a 1非零，故保留a 1取a 2，因为a 1与a 2线性无关，故保留a 1，a 2 取a 3，易得a 3=2a 1+a 2，故a 1，a 2 ，a 3线性相关。

所以最大无关组为a 1，a 2 方法2 初等变换法【定理】 矩阵A 经初等行变换化为B ，则B 的列向量组与A 对应的列向量组有相同的线性相关性. 证明从略,下面通过例子验证结论成立.向量组：α1=(1,2,3)T, α2=(-1,2,0)T, α3=(1,6,6)T由上可得，求向量组的最大线性无关组的方法： （1）列向量行变换①把向量组的向量作为矩阵的列向量组成矩阵A ； ②对矩阵A 进行初等行变换化为阶梯形矩阵B ；③A 中的与B 的每阶梯首列对应的向量组，即为最大无关组．【例3】求向量组 ：α1=(2,1,3,-1)T, α2=(3,-1,2,0)T, α3=(1,3,4,-2)T, α4=(4,-3,1,1)T的秩和一个最大无关组, 并把不属于最大无关组的向量用最大无关组线性表示。

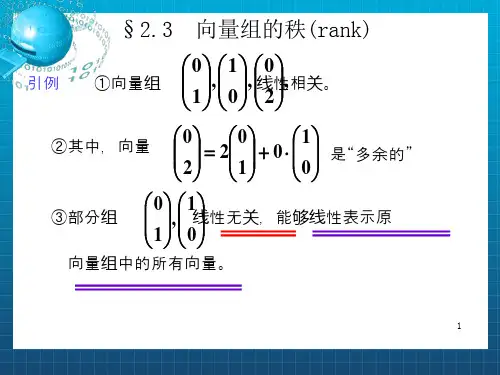
线性代数23向量组的秩

线性代数23向量组的秩

【示意】 向量组
1 ,2 , s
极大无关组
j1 , j2 , jr
定义
推论 任一向量组的两个极大无关组等价。
向量组≌ 极大无关组(I) 向量组≌ 极大无关组(II)
(I )≌(II) （传递性）
8
4、线性表示、线性关系、向量个数的有关结论
定理2 设向量组
1 , 2 ,, s
1 , 2 ,, t
16
例4．若向量组： 1 ,2 ,, s
可由向量组：
1 , 2 ,, t
线性表示，则必有（
C）
A．s≤t
B．s>t
C． r（Ⅰ）≤r（Ⅱ）
D． r（Ⅰ）>r（Ⅱ）
（I） （II）
【注】可以作为结论使用(即课后21题的结论)： 若(Ⅰ)可被(Ⅱ)线性表示，则 r(Ⅰ)≤r(Ⅱ).
17
课后习题 P86 15, 16, 17
解
1
0 1
1 3
3
2
10
1 2
11
1 2
11
1 2
1
1 2
2
6
2、向量组等价的基本性质
1)反身性： (I) ≌(I)
2)对称性： (I) ≌(II) (II) ≌
(I)
3)传递性： (I) ≌(II)及(II) ≌(II
I)
≌(III)
(I)
7
3、向量组与其极大无关组的关系
定理1 任一向量组与其极大无关组等价。
§2.3 向量组的秩(rank)
引例
①向量组
0 1
,
1 0
,
线02性,相关。
②其中，向量 02 2 10 0 10 是“多余的”

线性代数：LA2-2 向量组的秩

线性代数：LA2-2 向量组的秩

[b1,
b2
,,
bn
]
anb1 anb2 anbn an
故得 秩(A)≤1。又 A≠0，故 秩(A)≥1。于是， 秩(A)=1。
例 设A是m×n矩阵，B是n×m矩阵，并且AB = I， 则B的列向量组线性无关。
证明 （法一）因为 AB = I，所以
秩(B) ≥ 秩(AB) = 秩(I) = m 又
1 (1,1,1), 2(1,2,4), 3 (1,3,9)
证明：1,2 ,3 线性无关。
证明 令
1 1 1
A [1,2,3] 1 2 3
1 4 9
经验证 A满秩，即A可逆，所以 1, 2 , 3 线性无关。
例 （求极大无关组的方法）
已知向量组 1, 2 ,, n ，求它的秩及一个极
大无关组。
即 r(C ) r(B).
注 矩阵运算与矩阵秩的关系：
(1) 设A与B是同型矩阵，则 秩(A+B)≤秩(A)+秩(B)；
(2) 设A是s×n矩阵，B是n×t矩阵，则 ①秩(AB)≥秩(A)+秩(B) – n； ②秩(AB)≤min{秩(A)，秩(B)}； ③若AB = 0，则 秩(A)+秩(B) ≤ n；
的秩为___。
例 向量组 , （ , ）的秩为___。
定理 向量组 1, 2, …, m 线性相关的充分必要 条件是：秩{1, 2, …, m } < m。
定义 设向量组 1, 2, …, m 的秩为 r，则 1, 2, …, m 中任意 r 个线性无关的向量都称为向量 组 1, 2, …, m 的极大线性无关部分组，简称为
因 i1 , i2 , , ir 是 1, 2, …, m 的一个部分

10经管4—3向量组的秩

10经管4—3向量组的秩

∴列向量组的秩= r .
类似可证行向量组的情 形。
a11 a21 A = (α1 , α 2， ,α m ) = ⋯ ⋮ a n1
a12 ⋯ a1m a22 ⋯ a2 m ⋮ D⋮ ⋮ r an 2 ⋯ anm
Dr 所在的列 ——A中r个向量 构成矩阵的秩 线性无关！ 中 个向量 构成矩阵的秩=r 线性无关！
就是R 的一个最大无关组, 所以 e 1 , e 2 , …, en 就是 n 的一个最大无关组, 也有 R n 的秩是 n . 事实上， 事实上， R n中任何n个线性无关的向量的组a1 , a2 ,⋯ , an
都是其最大无关组！ 都是其最大无关组！
(R n 中任意 n+1 个 n 维向量都是线性相关的) 维向量都是线性相关的)
引入 向量组 A : α , α ,⋯，α 可由 向量组 B : β 1 , β 2 ,⋯，β m 1 2 m
线性表示 ⇔ R( A) = R( A, B )
A = (α1 , α 2 ,⋯，α m )
§3 向量组的秩
向量组 A : α1 , α 2 ,⋯，α m 线性相关 ⇔ R( A) = m 向量组 A : α1 , α 2 ,⋯，α m 线性无关 ⇔ R( A) < m 用向量组中向量构成的矩阵的秩说明问题， 不直接！ 用向量组中向量构成的矩阵的秩说明问题， 不直接！
的一个最大关组 最大关组及 例8（p91） 求R n 的一个最大关组及R n 的秩. （ ） 解 因为 n 维单位向量组e 1 , e 2 , …, en 是线性无关的 又R n 中任意 n+1 个 n 维向量都是线性相关的 （又R n 中任何一个向量都可由
e1 , e2 ,⋯ , en 线性表示） 线性表示）

2.4向量组的秩

2.4向量组的秩
i1 ,i2 ,...,ir 及 j1 , j2 ,..., jp
则 i1 ,i2 ,...,ir ≌ j1 , j2 ,..., jp
又据极大无关组的定义，i1 ,i2 ,...,ir 和 j1 , j2 ,..., jp 都线性无关, r p
定义2.13 向量组 1, 2,...,s 的极大无关组 所含向量的个数称为该向量组的秩, 记为 r(1, 2,...,s ) 或 秩(1, 2,...,s )
,
4
0 2
(Ⅰ)
此向量组 的一个极大无关组:
1
1
0
,
2
0
1
(Ⅱ)
(Ⅰ)与(Ⅱ)等价： 1 1102 2 01 12
3 1 2 4 01 22
1 1102 03 04 2 01 1203 04
推论 向量组的任意两个 极大无关组等价. 证 给定向量组 1, 2 ,..., r, r1, r2 ,...,s 设它有两个极大无关组：
1 1
,
4
0
2
1,2是此向量组的 一个极大无关组.
1,4 也是此向量组的一个极大线性无关组.
1,3 也是; 2 ,3 也是;
向量组的极大无关组 是不唯一的. 以下证明： 向量组 1,2,...,s 的任意两个极大无关组 所含向量的个数 相同.
定义2.12 设有两个向量组
1, 2 , ..., s ( Ⅰ ) 1, 2 , ..., t ( Ⅱ )
§2.4 向量组的秩
（一）向量组的极大无关组
例 考虑向量组
1
1
0
,
2
0 1
,
3
1 1 ,
4
0
2
此向量组线性相关.（维数2< 个数4 )

高等代数第二节 向量组的秩

高等代数第二节 向量组的秩
分析 证明向量组的一个部分组构成最大线性无 关组的基本方法就是：
根据最大线性无关组的定义来证，它往往还 与向量组的秩相联系．
证明 不失一般性,设 i1 , i2 ,, ir 是 1 , 2 ,, s中的任意r个线性无关的向量,于是对于任意 的 k (k 1,2,, s),向量组 i1 , i2 ,, ir , k 线性
解法二 对行向量组，可以先都转置为列向量，
排成矩阵后，用行变换化为行最简型
设
T :
2
0
2
1
α1T
2 4
,
α2T
2 1
,
α3T
0 3
,
α4T
1
0
4
5
1
4
显然 T 秩＝T 秩，且极大无关组互为转置向量
2 0 2 1
A α1T
α2T
α3T
α4T
2
4
2 1
0 3
因B组能由A组线性表示,故A组和B组合并而
成的向量组( A, B)能由A组线性表示. 而A组是( A, B)组的部分组,故A组总能由
( A, B)组线性表示. 所以( A, B)组与A组等价,因此
( A, B)组的秩也为r.
又因B组的秩为r , 故B组的最大无关组B0含r 个向量,因此B0组也是( A, B)组的最大无关组, 从 而( A, B)组与B0组等价.
rankT s
又 1线性无关，1秩＝r, 但1秩 秩，r s.
证毕
定理3 说明
(1) r个线性无关向量,若可用另一组向量线性表示， 则后一组向量的个数不少于r ;
(2) 一组线性无关的向量,不可能用另一组个数 更少的向量线性表示。 特别在三维向量空间中: (1)两个线性无关的向量，不能用同一个向量线性表 示； (2)三个线性无关的向量，不能用两个或一个向量 线性表示。 推论1 设向量组1秩为r,向量组2秩为s.若1可由2

线性代数43向量组秩-精选文档

线性代数43向量组秩-精选文档
a2 , a3 ; a1, a3 也是 A 的最大无关组。
课件 4
二、矩阵与向量组秩的关系
阵 的 秩 等 于 它 的 列 向 量 组 的 秩 ， 也 等 于 定理4 矩
它 的 行 向 量 组 的 秩 . 证 设 A ( a , a , , a ) ， R ( A ) r , 并 设 r 阶 子 式 D 0 . 1 2 m r
解

求最大无关组，即求出矩阵的最高阶非零 子式。将A变为最简形矩阵，可求出最高 阶非零子式。同时可求出A的最大线性无 关组与表示。
课件 8
1 1 1 2 2 1 1 2 1 4 例 2 设 矩 阵 A 4 6 2 2 4 9 7 9 3 6 求 矩 阵 A 的 列 向 量 组 的 一 个 最 大 无 关 组 ， 并 把 不 属 最 大 无 关 组 的 列 向 量 用 最 大 无 关 组 线 性 表 示 .
课件 2
向量组的秩
最 大 无 关 组 所 含 向 量 个 数 r 称 为 向 量 组 的 秩 .
只 含 零 向 量 的 向 量 组 没 有 最 大 无 关 组 ， 规 定 它 的 秩 为 0 .
课件
3
例如：对于向量组 A ：
a1 = ( 1, 2, －1), a2 = (2, －3, 1) , a3 = (4, 1, －1) 1 2 1 A 2 3 1 0 所以a1, a2 , a3线性相关。 4 1 1 a1, a2 为 A 的一个最大无关组; a ,a 线 性 无 关 ， 1 2
0 0 0 0 1 103 0 0
2
1 1 1 2 1 4 1 0 104 (r2 r3 ) ( ) r1 r2 r3 3 0 1 1 0 3 0 1 1 0 3

《线性代数教学PPT》向量组的秩

《线性代数教学PPT》向量组的秩

代
1,2, ,r为(A)的一个极大(最大)无关组 数
( A)的极大无关组必与(A)等价 : 最本质的性质.
注: (1)向量组的极大无关组不是唯一的.
=
(2)同一向量组的两个极大无关组间是等价的;
=
问题:如果(A)的极大无关组不唯一,问其任意
两个极大无关组所含向量个数是否唯一?
线
定理5 设有两个向量组: 性
数
1 2 3 0 1 2 3 0
=
0 1 1 1 0 1 1 1 所求秩为3. 0 0 12 0 0 0 1 0
=
0 0 12 0 0 0 0 0
例3.11: 求下列向量组的一个极大无关组及向量组的秩
1 (1,1, 2, 2,1)T ,2 (0, 2,1,5, 1)T ,3 (2, 0,3, 1,3)T ,
1 0
性
0 0 0
代
且有 3 21 2
1 0 0 2 0 1 0 1
数
这是因为1
2
4

3


0 0
0 0
1 0
0
0

=
0 0 0 0
=
例12 将 = (1,0,-4)T 用1 =(0,1,1)T,
2 =(1,0,1)T,3 =(1,1,0)T 线性表出.
2
5
1
4

0
5
5
2

0
5
5
2

数
1 1 3 1 0 1 1 2 0 1 1 2
1 0 2 1 1 0 2 1 1 0 2 0
0 1 1
0

0 1
1

线性代数—3.2 向量组的秩

线性代数—3.2 向量组的秩
• 齐次线性方程组的基础解系线性无关.
❖ 线性相关性 设有向量组 a1, , am , 如果存在一组不全为零的数
k1, , km , 使 k1a1 L kmam = 0
那么称 a1, , am 线性相关. 否则, 称 a1, , am 线性无关. • a1, , am 线性无关, 也即向量方程 x1a1 L xmam = 0 只有零解. ❖ 定理1
§3.2 向量组的秩
一、向量组的秩和最大无关组 二、向量组间的线性关系
❖ 齐次通解结构定理
设 x1, , xn-r (r = R(A))为 n 元方程组 Ax = 0 的解, 且 满足条件 R(x1, , xn-r) = n- r, 则 Ax = 0 的通解为
x = k1x1 L kn-rxn-r , (k1, , kn-r 为任意数) • 称 x1, , xn-r 为方程组 Ax = 0 的一个基础解系.
则向量 b 可由 a1, , ar 线性表示.
❖ 向量组的最大无关组 设向量组 A 的秩为 r, 如果 a1, , ar 为 A 的一个线性
无关部分组, 那么称 a1, , ar 为 A 的一个最大无关组.
❖ 最大无关组的性质 设 A 为一向量组, 则部分组 a1, , ar 为 A 的一个最大
无关组的充分必要条件是 (1) a1, , ar 线性无关; (2) A 中任一向量可由 a1, , ar 线性表示. 充分性: 设 b1, , bs 为 A 中向量, s > r. 存在数 kij , 使得
一、向量组的秩和最大无关组
设 A 为 n 维向量组( A {0}), 则 A 的任一线性无关部 分组所含向量个数不多于 n 个.
A 的线性无关部分组所含向量个数存在最大值: 存在正整数 r, 使得 A 中有 r 个向量线性无关, 而 A 中 任意多于 r 个向量(若存在的话)线性相关.

向量组的秩

向量组的秩

5 = −1 − 2 + 4
向量组中每一个向量由极大无关组的
向量线性表出的表达式是唯一 确定的。
例2
练习
求 矩阵A列向量组的一个极大无关组，并求出其
余向量由此极大无关组线性表出的表 达式
首非零元所在列对应的原来的向量分
别为
故
为其向量组的一个极大无关组
3 = −1 − 2
5 = 41 + 32 − 34
推论 1 两个等价的线性无关向量组个等价的向量组有相同的秩.
列向量组通过初等行变换不改变线性相关性!
向量组
矩阵
阶梯形矩阵
但再加上一个向量（秩为4<5）
就是线性相关的,
所以极大无关组就是左侧的列向量组，
显然，列向量组是线性无关的
（秩为 4）
即首非零元所在列对应的原来的向量组
例1
解：
1
0
0
0
0
1
0
0
3
1
0
0
2
1
1
0
1
0
1
0
所以 r(A)=3
首非零元所在列对应的原来的向量分别为
故
为其向量组的一个极大无关组
，
求出其余向量由此极大无关组线性表出的表达式
1
0
0
0
0
1
0
0
3
1
0
0
2
1
1
0
1
0
1
0
3 = 31 + 2
定理
1
0
0
0
0
1
0
0
3
1
0
0
0 −1

第2节向量组的秩（全）

第2节向量组的秩（全）

第2节向量组的秩（全）§2 向量组的秩回顾：矩阵的秩定义：在m×n 矩阵A中，任取k 行k 列(k≤m，k≤n),位于这些行列交叉处的k2 个元素，不改变它们在A中所处的位置次序而得的k 阶行列式，称为矩阵A的k 阶子式。

规定：零矩阵的秩等于零。

定义：设矩阵A 中有一个不等于零的r 阶子式D，且所有r+1 阶子式（如果存在的话）全等于零，那么D 称为矩阵A的最高阶非零子式，数r称为矩阵A的秩，记作R(A)。

结论：矩阵的秩= 矩阵中最高阶非零子式的阶数= 矩阵对应的行阶梯形矩阵的非零行的行数向量组的秩的概念定义1设向量组A中的一个部分组a, a2, …, a r ，满足1, a2, …, a r 线性无关；⑴a1⑵向量组A中任意r + 1个向量(如果有)都线性无关。

则称a, a2, …, a r 是向量组A的一个最大线性无关向量组(简称1最大无关组)；最大无关组所含向量个数r 称为向量组A的秩，记作R(A)。

例：求矩阵的秩，并求A 的一个最高阶非零子式．21112112144622436979A --?? ?-= ?---??第二步求A 的最高阶非零子式．选取行阶梯形矩阵中非零行的第一个非零元所在的列，与之对应的是选取矩阵A 的第一、二、四列．解：第一步先用初等行变换把矩阵化成行阶梯形矩阵．行阶梯形矩阵有3 个非零行，故R (A ) = 3．21112112141121401110~46224000133697900000r A -----= ? ?----0124211111(,,)~462367r A a a a -?? ? ?== ?-- ???0111011001000B ??= ?01240111011(,,)~462001367000r A a a a B ???? ? ?=== ? ?-- ?R (A 0) = 3，计算A 0的前3 行构成的子式21111180462-=-≠--因此这就是A 的一个最高阶非零子式。

第十次课 向量组的秩

第十次课 向量组的秩

1 8 5 3 4 2 1 3
可得R(A) = 3＜4 ，故向量组 α 1，α 2，α 3，α 4线性相关。
定理4.3.2(Steinitz定理) 设向量 α1 , α2 , , αq 可由向量组
β1 , β2 ,, β p 线性表示，如果 q
p
则 α1 , α2 , , αq 线性相关
所以 1，2 是向量组 1，2，3，4 的一个极大无关组。 同样2，4以及3，4也是一个极大无关组。
向量组 1=(0, 1)， 2=(1, 0)线性无关，且有任意三个向量线性相关
说明 1.含有非零向量的向量组总存在极大线性无关组
2．一个向量组的极大无关组不一定唯一
3．线性无关向量组的极大无关组就是其本身 4. 只含零向量的向量组没有极大无关组 例2．全体 n 维行向量构成的向量组记作 Rn ， 问题:Rn 中极大无关组所含向量的个数是多少? n维单位坐标向量组 e1=(1, 0, , 0)，e2=(0, 1, , 0)，
2 3 0 2 1 1 7 2 5 2 14 0 10 0 3 1
行变换
初等
1 0 0 0
2 1 1 0 1 0 0 1 0 0 0 0 0 0 3 0
1， 2， 4是该向量组的一个极大无关组
2. 求向量组的秩及极大无关组并判断线性相关性
2 0 1 1 2 0 2 = 1 , 2 , 3 , 4 , 5 0 0 1 3 0 0 0 0 0
2 2 3 4 1 2 2 1 4 r 0 0 2 6 1 6 2 2 0 5 0
3 = 21 2 2
(4) 若β Biblioteka ， 2， ， r是β 1， 2， ， m的极大无关组, β β β β 则α 1， 2， ， r是α 1， 2， ， m的极大无关组 α α α α

第三节 向量组的秩

第三节 向量组的秩
例如: A: 1=(1,0,0),2=(0,1,0) B: 1=(0,1,0),2=(0,0,1)
A的秩=2 B的秩=2
1可由1,2线性表示 但2不能由1,2线性表示
A与B不等价
∵A与B等价, 且都线性无关 A与B所含向量个数相同
可见,一个向量组的最大无关组虽然不 是唯一的,但最大无关组所含的向量的个数 总是确定的.
二、向量组的秩
定义10 向量组的最大无关组所含向量的 个数称为该向量组的秩. 注: (1)n维向量组Rn的秩是n.
(2)设向量组A: 1,2,,m
A线性无关A的最大无关组是A本身
3 : 1 1 5
1,2,3线性相关 3可由1,2线性表示
1 : 1 1 1
2 : 0 2 4 =0
4 : 2 0 6
1,2,4线性相关 4可由1,2线性表示 同理,5可由1,2线性表示 1,2是T的一个最大无关组
同法: 2,3也是T的一个最大无关组
注: (1)一般来说,一个向量组的最大无关组不是 唯一的. (2)一个向量组与它的最大无关组等价.
A中的向量线性表示,则称B可由A线性表示. 若A与B可互相线性表示,则称A与B等价.
等价性质: (1)反身性: A与A等价. (2)对称性: 若A与B等价,则B与A等价. (3)传递性: 若A与B等价,B与C等价,则A与C 等价.
定义9 一个向量组T中的部分向量1,2,, m若具有性质: (1)1,2,,m线性无关; (2)向量组T中任一向量都可由1,2,,m线
k11+k22++krr
(4) (5)
把(1)式代入(5)式,整理得:
k11+k22++krr
=k1(a111+a122++a1ss) +k2(a211+a222++a2ss) ++ kr(ar11+ar22++arss)

线性代数 3-2向量组的秩

线性代数 3-2向量组的秩
机动 目录 上页 下页 返回 结束
一、向量组的极大线性无关组
定义 若向量组 α1 , α 2 ,⋯ , α s 的部分组 α j , α j ,⋯ , α j 1. 1.定义 1 2 r :(1) α j1 , α j2 ,⋯ , α jr 线性无关 ; 满足 满足:(1) 线性无关; (2) 从向量组 α1 , α 2 ,⋯, α s 中任意另取一个向量 (若还 (2)从向量组 中任意另取一个向量( 添到α j , α j ,⋯, α j 中,所得新部分组都线性相关 . 有), ),添到 所得新部分组都线性相关. 1 2 r 则称 α j1 , α j2 ,⋯ , α jr 为向量组 α1 , α 2 ,⋯, α s 的一个极大 线性无关部分组 ,简称 极大无关组 . 线性无关部分组, 简称极大无关组 极大无关组.
(r = n) α1 α2 αn 重要结论：行变换不改变列向量间的线性关系 . 重要结论：行变换不改变列向量间的线性关系.
β
β 放末列. 可否由 α 1 ,⋯ , α s线性表示—— 竖排行变换， α1 ,⋯ , α s 是否线性相关—— 竖排行变换.
机动 目录 上页 下页 返回 结束
⇔
1. n个n维向量线性相关 (线性无关 定理 定理1. ) 线性无关)
对应分量不成比例，线性无关 2 1 2 −2 0 −1 T T T α1 ,α 2 ,α 3 = 4 1 3 = 4 1 3 =0
2 2 T T T α1 = 4 ,α 2 ,α4 2
0 1 1 0
1 2 3 −2 5= 4 2 2
繁！
0 1 0 −2 1 5 =0 0 2
机动 目录 上页
α1 , α 2 , α 3
⇔ 其排成的行列式值为 0 (不为 0) 其排成的行列式值为0 不为0)

向量组的秩-例题选讲

向量组的秩-例题选讲

A
14
证 因为向量组(I)可由(II) 线性表示, 故有
1k111k212 ks1s
r k1r1k2r2 ksrs
k11 k12
k1r
(1 ,2 , ,r) (1 ,2 , ,s) k 2 1 k 2 2
k
2r
(I)
(II)
k
s1
k s2
k sr
r r(1,2, ,r)r(BK) r ( K ) s
复习线性相关性的判定理论
单个向量组成的向量组 : (1)若 = 0, 则线性相关; (2)若 0, 则线性无关. 两个向量组成的向量组, :
(1)若对应分量成比例,则线性相关; (2)若对应分量不成比例,则线性无关.
A
1
设有n维向量组成的向量组:1,2,…,m
(1)包含0向量线性相关.
(m2)
(2) 1,2,4 是该向量组的一个极大无关组,
( 1,3,4 和 2,3也,是4 ).
(3) 31204 A
27
总结:向量组的有关结论
一、理解A=BC 二、 S的极大无关组 (1)定义
(2)S,则 可被极大无关组线表,且表法唯一
(3) S与极大无关组; 极大无关组～极大无关组 (4) S的各极大无关组含向量个数相等 --秩
定理4.4 r(An×m)=A的列向量组 1,2,,m的秩.
分析 记r(A)=r,往证 1,2, 的,秩m 为r, 即
只要证 1,2, 的,极m大无关组含r个向量.
证 r(A)= r
A存在r阶子式 Dr ≠0
记 Dr 对应的r 列为 ,i1 i2, ,ir ,
是r 维线性无关向量的接长,仍线性无关.
等价的向量组等秩

向量组的秩——精选推荐

向量组的秩——精选推荐

向量组的秩向量组的秩定义 3.5.1 极⼤⽆关组设在线性空间V中有⼀族向量S（其中可能只有有限个向量，也可能有⽆限个向量），如果在S中存在⼀组向量{α1,α2,⋯,αr}适合下列条件：1. α1,α2,⋯,αr线性⽆关；2. 这族向量中的任意⼀个向量都可以⽤α1,α2,⋯,αr线性表⽰，那么称{α1,α2,⋯,αr}是向量族S的极⼤线性⽆关组，简称极⼤⽆关组。

上述定义(2)表⽰若将S中任⼀向量α加⼊{α1,α2,⋯,αr}，则向量组{α1,α2,⋯,αr,α}⼀定线性相关。

命题 3.5.1 极⼤⽆关组的存在性设S是有限个向量组成的向量族且⾄少包含⼀个⾮零向量，则S r的极⼤⽆关组⼀定存在。

引理 3.5.1 向量组间个数关系设A,B是V中两组向量，A含有r个向量，B含有s个向量。

如果A中向量线性⽆关且A中每个向量均可⽤B中向量线性表⽰，则r≤s。

引理 3.5.1 的逆否命题⽤⼀句话来概括：“多”若可以⽤“少”来线性表⽰，则“多”线性相关。

引理 3.5.2 ⽆关组间个数关系设A,B都是V中线性⽆关的向量组，⼜A中任⼀向量均可⽤B中向量线性表⽰，B中任⼀向量也可⽤A中向量线性表⽰，则这两组向量所含的向量个数相等。

定理 3.5.1 向量族的极⼤⽆关组向量个数相等设A,B都是向量族S的极⼤线性⽆关组，则A,B所含的向量个数相等。

定义 3.5.2 向量族的秩向量族S的极⼤⽆关组所含的向量个数称为S的秩，记做rank(S)或r(S)。

定义 3.5.3 向量组等价若向量组A和B可以互相线性表⽰，则称这两个向量组等价。

定理 3.5.2 等价的向量组有相同的秩定义 3.5.4 基设V是数域K上的线性空间，若在V中存在线性⽆关的向量{e1,e2,⋯,e n}，使得V中任⼀向量均可表⽰为这组向量的线性组合，则称{e1,e2,⋯,e n}是V的⼀组基，线性空间V称为n维线性空间（具有维数n）。

如果不存在有限个向量组成V的⼀组基，则称V是⽆限维向量空间。

线代第四章(2)向量组的秩

线代第四章(2)向量组的秩

求该方程组的全体解向量构成的向量组S的秩。 求该方程组的全体解向量构成的向量组 的秩。 的秩 解
1 2 1 −2 A = 2 3 0 −1 1 −1 −5 7 x1 3 −4 x −2 3 2= c +c x3 1 1 2 0 x4 0 1
2
最大无关组的等价定义: 最大无关组的等价定义
设向量组 A0 : α 1 ,α 2 ,L ,α r
的一个部分组， 是向量组 A 的一个部分组，且满足 线性无关。 （i）向量组 A0 线性无关。 ） 线性表示。 （ii）向量组 A 的任一向量都能由向量组 A0 线性表示。 ） 的一个最大无关组。 那么向量组 A0 便是向量组 A 的一个最大无关组。 定理6 矩阵的秩等于它的列向量组的秩， 定理6：矩阵的秩等于它的列向量组的秩，也等于它行向量 组的秩。 组的秩。
1 2 3 2 1 3 5→ 0 0 1 2 0 3 2 0 1 1 → 0 1 1 0 0 0 0 1 2
向量用该最大无关组线性表示。 向量用该最大无关组线性表示。
2 解：设 A = 4 2 2 1 2 → 0 1 1 0 0 0
15
前面我们建立定理1、 、 时 前面我们建立定理 、2、3时，限制向量组只 含有限个向量，现在我们要去掉这一限制， 含有限个向量，现在我们要去掉这一限制，把定 推广到一般的情形. 理1、2、3推广到一般的情形 推广的方法是利用 、 、 推广到一般的情形 向量组的最大无关组作过渡. 如定理 3 可推广为 向量组的最大无关组作过渡
16
定理 3
设向量组 B：b1 , b2 , ··· , bl 能由向
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
齐次线性方程组AX=0有非零解
其中A=(1 2 … m), X=(x1,x2,…,xm)T (8)设有n个n维向量1,2,…,n: 1,2,…,n线性相关|1 2 … n|=0; 1,2,…,n线性无关|1 2 … n|0.
(9) Rn中n+1个向量一定线性相关. (10)矩阵判别法.
011
1
0
1
1

(1 2 3 ) (1
故两向量组等价,等秩,
2
3
)

1 0
1 1
0 1
r(1 2 3 ) r(1 2 3) 3.
则 1, 2, 3 线性无关.
19
4.3.3 向量组的秩与矩阵的秩的关系
定理4.4 r(An×m)=A的列向量组1,2, ,m的秩.
等价的向量组等秩
17
例2 设 1 1 2, 2 2 3, 3 3 1.
若向量组1, 2, 3线性无关,证明
向量组1, 2, 3也线性无关.
证1 由已知可以解得用1, 2,3 来表示
1, 2, 3的表达式:
2

1 2
(1

2

3
),
3
1
1 2
1 2
(1


2
(1 2

3) 3)
故两向量组等价,等秩, r(1 2 3)=3
r(1 2 3 ) =3 1, 2, 3 线性无关.
18
1 0 1
证2
(1

2

3
)=(1

2
3
)

1 0
1 1
0 1
101
Q 1 1 0 20
向量都线性相关. j (I如) 果j=1,…,r, j 显然可由1, 2 ,, r 线性表示;如果 j=r+1,…,m, 向量组1, 2 ,, r , j 一定
线性相关,所以 j ( j=r+1,…,m)可以由
1, 2 ,, r 线性表示 (I)可由(II)线性表示.
证 由1,2,…,m, 线性相关
存在不全为零的数k1,k2,…,km,l使得
k11 k22 L kmm l 0
下面证明只有l0, 反证法.
7
如果 l =0, 则有k1, k2,…,km不全为零,使
k11 k22 L kmm 0
于是1, 2, … , m 线性相关,与已知矛盾.
从而 l 0. 故有



k1 l
1

k2 l
2
L

km l

m
即 可由1, 2, … , m线性表示.
下面来证明表示的唯一性.
8
假若 有两种表示法,设
k11 k22 L kmm l11 l22 L lmm
两式相减,得
(k1 l1)1 (k2 l2)2 L (km lm)m 0
③表示系数对应相同
m
当i 时k j, j j 1 ji
m
i k j j j 1 ji
行初等变换不改变A的秩,不改变
列向量组之间的线性关系.
23
例4 求矩阵A列向量组的一个极大无关 组和秩, 并把其余列向量用所求出 的极大无关组线性表示.
1 2 1 0
A1 1
复习线性相关性的判定理论
单个向量组成的向量组 : (1)若 = 0, 则线性相关; (2)若 0, 则线性无关. 两个向量组成的向量组, :
(1)若对应分量成比例,则线性相关; (2)若对应分量不成比例,则线性无关.
1
设有n维向量组成的向量组:1,2,…,m
(1)包含0向量线性相关.
3
4.3 向量组的秩
本节 主要内容
1. 极大线性无关组与秩; 2. 向量组的等价; 3.向量组的秩与矩阵的秩的关系.
4
4.3.1 向量组的极大无关组与秩
定义1 设S是n维向量构成的向量组,在S中
选取r个向量 1,2,,如,果r满足
(1) 1,2,L ,r线性无关 (2)任取 S,总有 ,1,线2,L性,相r关.
求向量组的秩和极大无关组.
解 因 1 , 2 线性无关 ,且 3 = 1+ 2
所以1 , 2为极大无关组,
故
秩( 1, 2 , 3 ) =2.
可知1 , 3和2 , 3也都是极大无关组.
6
线性表示唯一性定理
定理4.2 设n维向量1,2,…,m线性无关, 而1,2,…,m , 线性相关, 则 可由 1,2,…,m 线性表示, 且表法唯一.
001
2 , 3 , 4是该向量组的一个极大无关组.
26
解法2
1120
设 A=(1,2,3,4 )=
由1,2,…,m 线性无关,得
ki li (i 1, 2,L , m) 故 可由1,2,…,m 唯一线性表示.
9
4.3.2 向量组的等价
定义2 设有两个 n 维向量组
(I) 1,2,L ,r; (II) 1, 2,L , s
若(I)中每个向量都可由(II)线性表示, 则称 向量组(I)可由向量组(II)线性表示.
若(I)线性无关,且(I)可由(II)
线性表示,则 r ≤ s .
14
证 因为向量组(I)可由(II) 线性表示, 故有
1


k111

k21
LL
2

L
ks1 s
r k1r 1 k2r 2 L ksr s
k11 k12 L k1r
(1,2 ,L
不妨设(II) 1,2 ,L ,r 是(I)的一个
极大无关组.
12
(1) i ( i = 1,2,…,r) (II), 由 i 01 L 1i L 0r 0r1 L 0m
即(II) 可由(I) 线性表示.
(2)由定义1知, 1, 2 ,, m中任意r+1个
且r >s, 则(I) 线性相关.
推论2 若(I)、(II)都线性无关,且(I)与(II)
等价,则 r = s .
等价的无关向量组必然等秩
向量组的两个极大无关组所含向量个数相等 推论3 若(I)可由(II)线性表示,则
秩(I)≤秩(II) .
16
证 设r(I)=r , r(II)=s , (I´),(II´)分别是(I), (II) 的极大无关组,显然(I´), (II´)含向量的 个数分别是r 与 s . 因为(I´)可由(I) 线性表示, (I)可由(II) 线性表示,而(II)可由(II´)线性表示,所以 (I´)可由(II´)线性表示.由定理4.3有r s.
分析 记r(A)=r,往证 1,2,的,秩m为r, 即
只要证 1,2,的,极m大无关组含r个向量.
证 r(A)= r
A存在r阶子式 Dr ≠0
记 Dr 对应的r 列为 i1 ,i2 ,L ,ir ,
是r 维线性无关向量的接长,仍线性无关.
j A, 下证 j ,i1 ,i2 , ,ir
(m2)
(2)包含成比例的向量线性相关.
(3)线性相关存在一个向量可由其余的
向量线性表示.
(4)线性无关任何向量都不能由其余的
向量线性表示.
(5) 增加(减少)个数不改变相(无)关性.
(6) 增加(减少)维数不改变无(相)关性.
2
(7) 向量组1,2,…,m线性相关性 x11+x22+…+xmm=0有非零解
25
例5 设有向量组
1
1
2
0
1=
0 1
， 2=
1 0
， 3=
1 1
， 4=
0 1
0
0
0
1
求向量组的(1)秩;(2)极大无关组;(3)表示系数.
解法1
1120
设 A= (1,2,3,4 )= 0 1 1 =1≠0 而 |A|=0 知秩=3,
Bi=0, i=1,…,mB=0. 其余情况可以类似得到.
22
极大无关组和秩的求法
初等变换法 n维列向量组S: 1,2 ,L ,m 将A=(1,2, ,m ) 行 (1, 2, , m)=B 则向量组 1,2 ,L与,m 1, 2,L , m
①秩等; ②极大无关组的位置对应相同;
4 3
1 0
4 2

1 2 3 4
解 通过初等行变换把A化为行最简形
1 2 1 0 1 2 1 0 A 1 4 1 4 0 2 2 4
1 3 0 2 0 1 1 2
24
1 2 1 0 1 2 1 0 0 2 2 4 0 1 1 2
是线性相关的,
20
因为 ① j 在 i1 , i2 , …,ir 中; j ,i1 ,i2 , ,ir线性相关.
② j 不在 i1 , i2 , …,ir 中,
r+1列对应的子矩阵记为A1 ,
而
r(A1)≤ r(A)= r ＜r +1
所以 j ,i1 ,i2线,性,相ir 关,
则称向量组 1,2,为,向r量组S的一个
极大线性无关组(简称极大无关组). 数 r 称为该向量组的秩,记为
r(1, 2, … , s)= r 或秩(1, 2, … , s)= r
5
例1 设有向量组 1 = (1, 1, 1)T, 2 =(2,1, 0)T, 3 =(3,2,1)T,
0 1 1 2 0 0 0 0
1 0 3 4 1 0 3 4 0 1 1 2 0 1 1 2 B
0 0 0 0 0 0 0 0