稳态误差

matlab稳态误差
摘要：
一、稳态误差的概念
二、MATLAB求解稳态误差的方法
三、实例分析
四、总结
正文：
稳态误差是指在系统输入信号发生变化时，输出信号达到稳定状态时，系统输出与期望输出之间的差异。

在控制系统中，稳态误差是一个重要的性能指标，它直接影响到系统的控制精度。

MATLAB是一种功能强大的数学软件，可以用于求解系统的稳态误差。

MATLAB求解稳态误差的方法主要有两种：一种是利用控制系统的传递函数，通过求解系统的零点和极点来确定系统的稳态误差；另一种是利用MATLAB提供的稳态误差计算函数，例如`dcgain`函数。

下面通过一个实例来演示如何利用MATLAB求解系统的稳态误差。

假设我们有一个线性系统，其传递函数为：
G(s) = 2 / (s^2 + 3s + 2)
我们可以通过以下步骤求解该系统的稳态误差：
1.首先，利用MATLAB计算系统的开环增益，即：
G_open(s) = 1 / (s^2 + 3s + 2)
2.然后，利用`dcgain`函数求解系统的稳态误差，即：
ess_error = dcgain(num, den)
其中，`num`和`den`分别是系统的分子和分母多项式的系数。

3.最后，我们可以将结果输出到MATLAB的命令窗口，或者将其保存到文件中，以便后续分析。

综上所述，MATLAB提供了一种方便快捷的方法来求解系统的稳态误差。

通过实例分析，我们可以看到，利用MATLAB求解稳态误差的过程简单易行，只需要几个简单的步骤就可以得到结果。

稳态误差的总结分析和例解控制系统稳态误差是系统控制准确度的一种度量，通常称为稳态性能。

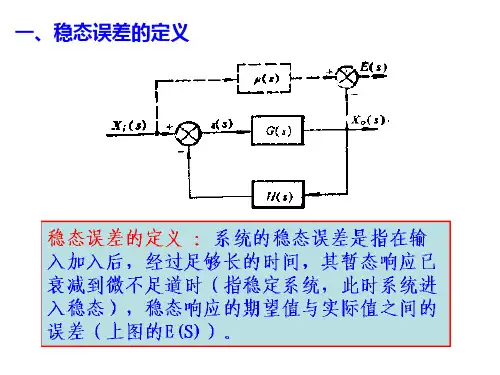
只有当系统稳定时，研究稳态误差才有意义，对不能稳定的系统，根本不存在研究稳态误差的可能性。

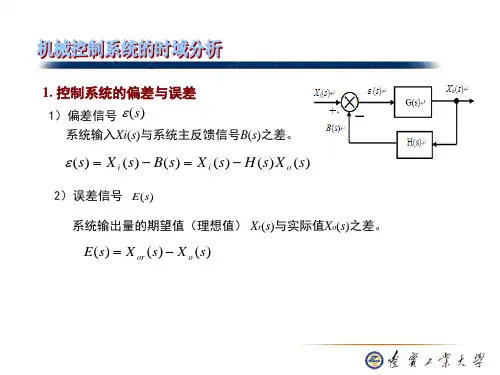
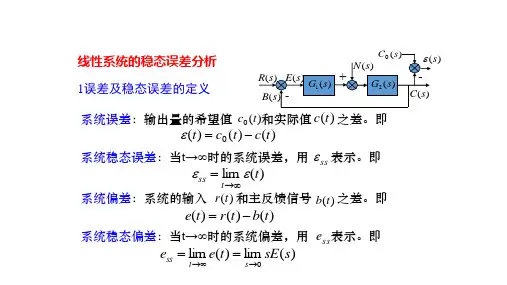
一、 误差与稳态误差1、输入端的定义：对图一，比较输出得到：E(s)=R(s)-H(s)*Y(s)称E(s)为误差信号，简称误差图一2、输出端的定义：将图一转换为图二，便可定义输出端的稳态误差，并且与输入端的稳态误差有如下关系：E ’(s)=E(s)/H(s)输入端定义法可测量实现，输出端定义法常无法测量，因此只有数学意义，以后在不做特别说明时，系统误差总是指输入端定义误差。

图二再有误差的时域表达式：也有：e(t)=L −1[E(S)]=L −1[Φe (s)*R(S)]其中Φe (s)是误差传递函数，定义为：Φe (s)=E sR (S )=11+G s ∗H s根据拉氏变换终值定理，由上式求出稳态误差：(T j s+1)e ss (∞)=lim s →0s ∗E (s )=lim s →0s∗R (S )1+G s ∗H s二、 系统类型一般的，定义一个分子为m 阶次，分母为n 阶次的开环传递函数为：[]1()()()()ts ss e t L E s e t e t -==+G(S)H(S)=K (Tis +1)m i =1s ^v (Tjs +1)n −vj =1K 为开环增益，ν表示系统类型数，ν=0，表示0型系统；ν=1表示Ⅰ型系统；当ν大于等于2时，除了符合系统外，想使得系统稳定相当困难。

四、阶跃输入下的e ss (∞)与静态位置误差系数Kpr(t)=R*1(t),则有：e ss (∞)= R1+K ,ν=00 ,ν≥1用Kp 表示静态位置误差系数：e ss (∞)=R 1+lim s →0G s ∗H s =R1+Kp其中： Kp=lim s →0G s ∗H s且有一般式子：Kp=K ,ν=0∞ ,ν>=1五、斜坡输入下的e ss (∞)与静态速度误差系数Kvr(t)=Rt,则有：e ss (∞)= ∞ ,ν=0RK ,v =10,v ≥2用Kv 表示静态速度误差系数：e ss (∞)=R lim s →0G s ∗H s =RKv其中：Kv=lim s →0s ∗G s ∗H s六、加速度输入下的e ss (∞)与静态加速度误差系数Kar(t)=Rt 2/2,则有：e ss (∞)= ∞ ,ν=0、1R/K,v =20 ,v ≥3用Kv 表示静态速度误差系数：e ss (∞)=R lim s →0G s ∗H s =RKa其中：Kv=lim s →0s ^2∗G s ∗H s且有：Ka= 0, v =0、1K , v =2∞, v ≥3七、扰动状况下的稳态误差系统的模型如图三所示对扰动状况下的稳态误差仍然有输入端与输出端的两种定义：图三1、输入端定义法：扰动状况下的系统的稳态误差传递函数：由拉氏变换终值定理，求得扰动状况下的稳态误差为：2、输出端定义法：212()'()0()()1()()()G s E s Y s N s G s G s H s =-=-+记Φe (s) =−G 2 s1+G s 为误差传递函数，其中G(s)为：G(s)=G 1(s)*G 2(s)*H(s)八、减小或者消除稳态误差的措施： （1）保证系统中各个环节（或元件），特别是反馈回路中元件的参数具有一定的精度和恒定性；（2）对输入信号而言，增大开环放大系数（开环增益），以提高系统对给定输入的跟踪能力；（3）对干扰信号而言，增大输入和干扰作用点之间环节的放大系数（扰动点之前的前向通道增益），有利于减小稳态误差；（4）增加系统前向通道中积分环节数目，使系统型号提高，可以消除不同输入信号时的稳态误差。

已知闭环传递函数求稳态误差已知闭环传递函数求稳态误差引言：在控制工程中，闭环传递函数被广泛应用于描述控制系统的性能和稳定性。

稳态误差是评估控制系统性能的重要指标之一，它表示在稳定状态下系统输出与期望输出之间的偏差。

本文将详细探讨已知闭环传递函数的情况下如何求解稳态误差，以及其中的关键概念和方法。

一、稳态误差的定义和分类稳态误差是指在稳定状态下系统输出与期望输出之间的差异。

它通常用于评估控制系统对不同输入信号的跟踪能力。

稳态误差可以分为三类：零误差、有限非零误差和无穷大误差。

零误差表示系统能够完全跟踪期望输入信号，也即系统输出与期望输出完全一致。

有限非零误差表示系统输出与期望输出之间存在一定的差异，但这种差异是有限的，可以通过参数调整来减小。

无穷大误差表示系统无法跟踪期望输入信号，输出与期望输出之间的差异会趋于无穷大。

二、已知闭环传递函数求解稳态误差的方法已知闭环传递函数的情况下，我们可以使用不同的方法来求解稳态误差。

以下是常用的两种方法：1. 误差常数法误差常数法是一种基于稳态误差的定义和概念来求解稳态误差的方法。

对于单位阶跃输入信号（step function），我们可以通过计算系统输出的稳态值与期望输出的稳态值之间的差异，来求解稳态误差。

具体来说，我们可以将闭环传递函数表示为最简形式，即传递函数的分子次数小于或等于分母次数，然后根据其特性来求解稳态误差。

常见的误差常数包括静态误差常数、速度误差常数和加速度误差常数。

通过计算这些误差常数，我们可以得到稳态误差的近似解。

2. 根轨迹法根轨迹法是一种基于闭环传递函数的极点位置和稳态误差之间的关系来求解稳态误差的方法。

通过根轨迹的分析，我们可以确定系统极点的位置，从而评估系统的稳态误差。

一般来说，系统极点越接近原点，稳态误差越小；系统极点越远离原点，稳态误差越大。

通过绘制根轨迹图，并结合稳态误差定义，我们可以准确地求解稳态误差。

三、个人观点和理解在控制工程中，求解稳态误差是非常重要的，它直接关系到控制系统的性能和稳定性。