实验四 线性定常系统的稳态误差
- 格式:doc
- 大小:491.50 KB
- 文档页数:10


线性系统的校正实验报告翻译:摘要:本实验通过给定的线性系统对其进行校正,在不同的频率下对系统进行稳态和瞬态测试,通过测试结果分析系统性能和误差,掌握线性系统的基本原理和校正方法。
引言:线性系统广泛应用于各种工业、科技领域,而线性系统的准确度和稳定性关系到整个系统的效率和安全性。
因此,对线性系统进行校正是保证其正常运行的必要手段。
本实验将针对一个给定的线性系统进行校正,分析其校正效果。
实验设计:1. 实验仪器本实验要求使用信号发生器、数字脉冲计数器和示波器。
2. 实验内容(1)信号发生器的设置设置输出波形类型和频率,使其跟线性系统的工作频率相同。
(2)数字脉冲计数器的设置通过数字脉冲计数器测试稳态和瞬态响应,并对脉冲计数器进行校准。
(3)示波器的设置观测线性系统的输出信号,分析系统的稳态和动态响应。
(4)线性系统的测试使用信号发生器输入不同频率的正弦波和方波信号,观测输出信号,并记录数字脉冲计数器的计数。
3.实验步骤(1)准备工作将信号发生器和示波器连接线性系统的输入和输出接口,调节信号发生器的频率和幅度。
(2)瞬态响应测试在信号发生器上输入方波信号,在示波器上观测输出信号的瞬态响应,通过计数器获取相关数据。
在信号发生器上输入正弦波信号,通过调整幅度和相位,使其和线性系统的工作频率相同,记录计数器的数据,并分析系统的稳态响应。
结果分析:通过本实验的测试,得到了不同频率下线性系统的稳态和瞬态响应。
观察稳态响应的幅频响应曲线,分析系统的性能。
通过瞬态响应和数字脉冲计数器的数据,计算误差,判断系统的准确度和稳定性。
运用基本的线性系统校准方法对系统进行校准,进一步提高系统的准确度和稳定性。
结论:。


本科实验报告课程名称:自动控制原理实验项目:控制系统的稳定性和稳态误差实验地点:多学科楼机房专业班级:学号:学生姓名:指导教师:2012 年5 月15 日一、实验目的和要求:1.学会利用MATLAB 对控制系统的稳定性进行分析; 2.学会利用MATLAB 计算系统的稳态误差。
二、实验内容和原理:1.利用MATLAB 描述系统数学模型如果系统的的数学模型可用如下的传递函数表示nn n m m m a s a s b s b s b s U s Y s G ++++++==-- 11110)()()( 则在MATLAB 下,传递函数可以方便的由其分子和分母多项式系数所构成的两个向量惟一确定出来。
即num=[b 0,b 1 ,…, b m ]; den=[1,a 1,a 2 ,…,a n ]例2-1 若系统的传递函数为5234)(23+++=s s s s G 试利用MA TLAB 表示。
当传递函数的分子或分母由若干个多项式乘积表示时,它可由MA TLAB 提供的多项式乘法运算函数conv( )来处理,以获得分子和分母多项式向量,此函数的调用格式为 p=conv(p1,p2)其中,p1和p2分别为由两个多项式系数构成的向量,而p 为p1和p2多项式的乘积多项式系数向量。
conv( )函数的调用是允许多级嵌套的。
例2-2 若系统的传递函数为)523)(1()66(4)(232++++++=s s s s s s s s G试利用MA TLAB 求出其用分子和分母多项式表示的传递函数。
2.利用MATLAB 分析系统的稳定性在分析控制系统时,首先遇到的问题就是系统的稳定性。
判断一个线性系统稳定性的一种最有效的方法是直接求出系统所有的极点,然后根据极点的分布情况来确定系统的稳定性。
对线性系统来说,如果一个连续系统的所有极点都位于左半s 平面,则该系统是稳定的。
MATLAB 中根据特征多项式求特征根的函数为roots( ),其调用格式为r=roots(p) 其中,p 为特征多项式的系数向量;r 为特征多项式的根。

实验一 典型环节的电路模拟一、实验目的1.熟悉THKKL-5型 控制理论·计算机控制技术实验箱及“THKKL-5”软件的使用; 2.熟悉各典型环节的阶跃响应特性及其电路模拟;3.测量各典型环节的阶跃响应曲线,并了解参数变化对其动态特性的影响。
二、实验设备1.THKKL-5型 控制理论·计算机控制技术实验箱;2.PC 机一台(含“THKKL-5”软件)、USB 数据采集卡、37针通信线1根、16芯数据排线、USB 接口线。
三、实验内容1.设计并组建各典型环节的模拟电路;2.测量各典型环节的阶跃响应,并研究参数变化对其输出响应的影响。
四、实验原理自控系统是由比例、积分、微分、惯性等环节按一定的关系组建而成。
熟悉这些典型环节的结构及其对阶跃输入的响应,将对系统的设计和分析十分有益。
本实验中的典型环节都是以运放为核心元件构成,其原理框图 如图1-1所示。
图中Z 1和Z 2表示由R 、C 构成的复数阻抗。
1.比例(P )环节比例环节的特点是输出不失真、不延迟、成比例地复现输出信号的变化。
图1-1 它的传递函数与方框图分别为:KS U S U S G i O ==)()()(当U i (S)输入端输入一个单位阶跃信号,且比例系数为K 时的响应曲线如图1-2所示。
2.积分(I )环节 图1-2积分环节的输出量与其输入量对时间的积分成正比。
它的传递函数与方框图分别为:设U i (S)为一单位阶跃信号,当积分系数为T 时的响应曲线如图1-3所示。
TsS U S Us G i O1)()()(==图1-33.比例积分(PI)环节比例积分环节的传递函数与方框图分别为:)11(11)()()(21211212CSR R R CSR R R CSR CS R S U S U s G i O +=+=+==其中T=R 2C ,K=R 2/R 1设U i (S)为一单位阶跃信号,图1-4示出了比例系数(K)为1、积分系数为T 时的PI 输出响应曲线。


实验四线性定常控制系统的稳定分析
一、实验目的
(1)深刻理解反馈对系统稳定性的作用和影响;
(2)深刻理解系统类型对系统稳定性的影响的规律;
(3)深刻理解零点对系统稳定性无影响;
(4)理解系统参数对系统稳定性的影响。
二、实验原理及内容:
1.单位反馈对系统稳定性的影响
(1) 已知开环系统结构图如图4-1所示。
R (S
其中W(S)分别为:(a )1()0.11W s s =+和(b )1()0.2
W s s =- (2)闭环系统单位负反馈形式为:
图4-2 闭环系统
其中W(S)同(1)。
通过观察两组W (S )在开环和闭环两种形式下系统的零、极点分布和单位阶跃响应曲。
《自动控制理论》实验教学大纲课程名称:自动控制理论课程性质:非独立设课使用教材:自编课程编号:面向专业:自动化课程学分:考核方法:成绩是考核学习效果的重要手段,实验成绩按学生的实验态度,独立动手能力和实验报告综合评定,以20%的比例计入本门课程的总成绩。
实验课总成绩由平时成绩(20%)、实验理论考试成绩(40%)、实验操作考试成绩(40%)三部分组成,满分为100分。
实验理论考试内容包含实验原理、实验操作方法、实验现象解析、实验结果评价、实验方案设计等。
考试题型以填空、判断、选择、问答为主,同时可结合课程特点设计其他题型。
实验操作考试根据课程特点设计若干个考试内容,由学生抽签定题。
平时成绩考核满分为20分,平时成绩= 平时各次实验得分总和÷实验次数(≤20分)。
每次实验得分计算办法为:实验报告满分10分(其中未交实验报告或不合格者0分,合格6分,良好8分,优秀10分);实验操作满分10分(其中旷课或不合格者0分,合格6分,良好8分,优秀10分)。
撰写人:任鸟飞审核人:胡皓课程简介:自动控制理论是电气工程及其自动化专业最主要的专业基础必修课。
通过本课程的各个教学环节的实践,要求学生能熟练利用模拟电路搭建需要的控制系统、熟练使用虚拟示波器测试系统的各项性能指标,并能根据性能指标的变化分析参数对系统的影响。
实验过程中要求学生熟悉自动控制理论中相关的知识点,可以在教师预设的实验前提下自己设计实验方案,完成实验任务。
教学大纲要求总学时80,其中理论教学68学时、实验12学时,实验个数6个。
9采样控制系统的分析√4选做10采样控制系统的动态校正√4选做合计实验一典型环节的电路模拟一、实验类型:综合性实验二、实验目的:1.熟悉THBCC-1型实验平台及“THBCC-1”软件的使用;2.熟悉各典型环节的阶跃响应特性及其电路模拟;3.测量各典型环节的阶跃响应曲线,并了解参数变化对其动态特性的影响。
三、实验内容与要求:1.设计并组建各典型环节的模拟电路;2.测量各典型环节的阶跃响应,并研究参数变化对其输出响应的影响;3.画出各典型环节的实验电路图,并注明参数。
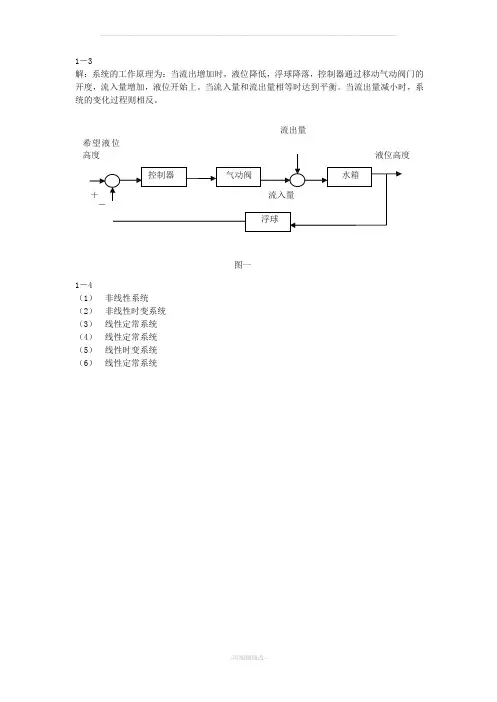
1-3解:系统的工作原理为:当流出增加时,液位降低,浮球降落,控制器通过移动气动阀门的开度,流入量增加,液位开始上。
当流入量和流出量相等时达到平衡。
当流出量减小时,系统的变化过程则相反。
流出量希望液位图一1-4(1)非线性系统(2)非线性时变系统(3)线性定常系统(4)线性定常系统(5)线性时变系统(6)线性定常系统2 2-1 解:显然,弹簧力为 k x (t ) ,根据牛顿第二运动定律有:F (t ) − kx (t ) = m移项整理,得机械系统的微分方程为:d 2 x (t ) dt 2m d x (t ) + kx (t ) = F (t ) dt 2对上述方程中各项求拉氏变换得:ms 2 X (s ) + kX (s ) = F(s )所以,机械系统的传递函数为:G (s ) = X (s ) =F (s )1ms 2 + k2-2 解一:由图易得:i 1 (t )R 1 = u 1 (t ) − u 2 (t ) u c (t ) + i 1 (t )R 2 = u 2 (t ) du c (t )i 1 (t ) = Cdt由上述方程组可得无源网络的运动方程为:C ( R + R ) du 2 (t ) u (t ) = CRdu 1 (t ) u (t )1 2 dt+ 2 2+ 1 dt对上述方程中各项求拉氏变换得:C (R 1 + R 2 )sU 2 (s ) + U 2 (s ) = CR 2 sU 1 (s ) + U 1 (s )所以,无源网络的传递函数为:G (s ) = U 2 (s )=U 1 (s )1 +sCR 21 + sC (R 1 +R 2 )解二(运算阻抗法或复阻抗法):U (s ) 1 + R 2 1 + R Cs2 = Cs = 2U (s ) R + 1 + R 1 + ( R + R )Cs 1 1 21Cs22-5 解:按照上述方程的顺序,从输出量开始绘制系统的结构图,其绘制结果如下图所示:依次消掉上述方程中的中间变量 X 1 , X 2 , X 3 , 可得系统传递函数为:C (s ) = R (s )G 1 (s )G 2 (s )G 3 (s )G 4(s )1 + G2 (s )G3 (s )G 6 (s ) + G 3 (s )G4 (s )G5 (s ) + G 1 (s )G 2 (s )G 3 (s )G 4 (s )[G 7 (s ) −G 8 (s )]2-6 解:①将G1 (s) 与G1 (s) 组成的并联环节和G1 (s) 与G1 (s) 组成的并联环节简化,它们的等效传递函数和简化结构图为:G12 (s) = G1(s) + G2(s)G34 (s) = G3(s) −G4(s)②将G12 (s), G34 (s) 组成的反馈回路简化便求得系统的闭环传递函数为:2-7 解:C(s)=R(s)G12(s)1 + G12(s)G34(s)=G1(s) + G2(s)1 + [G1(s) + G2(s)][G3(s) −G4(s)]由上图可列方程组:[E(s)G1 (s) −C(s)H2(s)]G2(s) = C(s)R(s) −H1(s)C(s)G2(s)= E(s)联列上述两个方程,消掉E(s) ,得传递函数为:C(s)= R(s)G1(s)G2(s)1 + H1(s)G1(s) + H2(s)G2(s)联列上述两个方程,消掉C(s) ,得传递函数为:E(s)= R(s)1 + H2(s)G2(s)1 + H1(s)G1(s) + H2(s)G2(s)1 2 22 32-8 解:将①反馈回路简化,其等效传递函数和简化图为: 0.4G (s ) = 2s + 1 = 1 +0.4 * 0.5 2s + 11 5s + 3将②反馈回路简化,其等效传递函数和简化图为:1G (s ) =s + 0.3s + 1= 5s + 321 + 0.45s +4.5s+ 5.9s + 3.4(s + 0.3s + 1)(5s + 3)将③反馈回路简化便求得系统的闭环传递函数为:0.7 * (5s + 3)Θo (s)= 5s 3 + 4.5s 2 + 5.9s + 3.4 =3.5s + 2.1Θi (s) 1 + 0.7 * Ks(5s + 3)5s 3+ (4.5 + 3.5K )s2+ (5.9 + 2.1K )s + 3.42 5s3-3 解:该二阶系统的最大超调量:σp =e−ζπ/1−ζ2*100%当σp= 5% 时,可解上述方程得:ζ= 0.69当σp= 5% 时,该二阶系统的过渡时间为:ts≈3ζwn所以,该二阶系统的无阻尼自振角频率w n 3-4 解:≈3ζts=30.69* 2= 2.17由上图可得系统的传递函数:10 * (1 + Ks)C (s)= R(s)s(s + 2)1 +10 * (1 + Ks)s(s + 2)==10 * (Ks +1)s + 2 * (1 +5K )s +10所以w n =10 ,ζw n =1+5K⑴若ζ= 0.5 时,K≈0.116所以K≈0.116 时,ζ= 0.5⑵系统单位阶跃响应的超调量和过渡过程时间分别为:σp =e−ζπ/1−ζ2*100% =e−0.5*3.14/1−0.52*100%≈16.3%ts= 3ζwn =30.5 *≈1.910⑶加入(1 + Ks )相当于加入了一个比例微分环节,将使系统的阻尼比增大,可以有效地减小原系统的阶跃响应的超调量;同时由于微分的作用,使系统阶跃响应的速度(即变w 2 1 2 p化率)提高了,从而缩短了过渡时间:总之,加入 (1 + Ks ) 后,系统响应性能得到改善。

实验四 线性定常系统稳态误差的研究一、实验目的1. 通过本实验,理解系统的跟踪误差与其结构、参数与输入信号的形式、幅值大小之间的关系;2. 研究系统的开环增益K 对稳态误差的影响。
二、实验设备同实验一。
三、实验内容1. 观测0型二阶系统的单位阶跃响应和单位斜坡响应,并实测它们的稳态误差;2. 观测I 型二阶系统的单位阶跃响应和单位斜坡响应,并实测它们的稳态误差;3. 观测II 型二阶系统的单位斜坡响应和单位抛物坡,并实测它们的稳态误差。
四、实验原理通常控制系统的方框图如图4-1所示。
其中G(S)为系统前向通道的传递函数,H(S)为其反馈通道的传递函数。
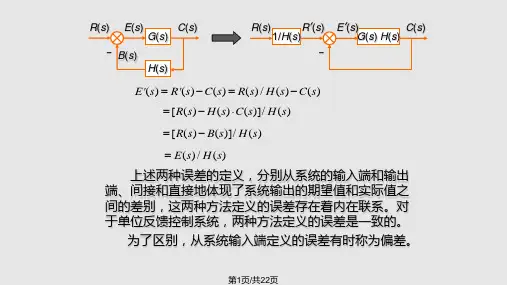
图4-1由图4-1求得)()()(11)(S R S H S G S E += (4.1)由上式可知,系统的误差E(S)不仅与其结构和参数有关,而且也与输入信号R(S)的形式和大小有关。
如果系统稳定,且误差的终值存在,则可用下列的终值定理求取系统的稳态误差:)(lim 0S SE e s ss →= (4.2)本实验就是研究系统的稳态误差与上述因素间的关系。
下面叙述0型、I 型、II 型系统对三种不同输入信号所产生的稳态误差ss e 。
1.0型二阶系统设0型二阶系统的方框图如图4-2所示。
根据式(4.2),可以计算出该系统对阶跃和斜坡输入时的稳态误差:图4-2 0型二阶系统的方框图1) 单位阶跃输入(sS R 1)(=) 3112)1.01)(2.01()1.01)(2.01(lim 0=⨯+++++⨯=→S S S S S S e S ss 2) 单位斜坡输入(21)(s S R =)∞=⨯+++++⨯=→2012)1.01)(2.01()1.01)(2.01(lim SS S S S S e S ss 上述结果表明0型系统只能跟踪阶跃输入,但有稳态误差存在,其计算公式为: Pss K R e +=10, 其中)()(lim 0S S H S G K p →≅,R 0为阶跃信号的幅值。
控制系统的稳定性分析实验报告一、实验目的1.了解控制系统的稳定性分析方法。
2.通过实验,掌握系统稳态误差、系统阻尼比、系统根轨迹等稳态分析方法。
3.掌握控制系统的稳定性分析实验步骤。
二、实验原理1.系统稳态误差分析系统稳态误差是指系统在达到稳态时,输出与输入之间的偏差。
对于稳态误差的分析,可以采用开环传递函数和闭环传递函数进行分析。
开环传递函数:G(s)闭环传递函数:G(s)/(1+G(s)H(s))其中,H(s)为系统的反馈环节,G(s)为系统的前向传递函数。
稳态误差可以分为静态误差和动态误差。
静态误差是指系统在达到稳态时,输出与输入之间的偏差;动态误差是指系统在达到稳态时,输出与输入之间的波动。
2.系统阻尼比分析系统阻尼比是指系统在达到稳态时,振荡的阻尼程度。
阻尼比越大,系统越稳定;阻尼比越小,系统越不稳定。
系统阻尼比的计算公式为:ζ=1/(2ξ)其中,ξ为系统的阻尼比,ζ为系统的阻尼比。
3.系统根轨迹分析系统根轨迹是指系统的极点随着控制参数变化而在复平面上的轨迹。
根轨迹分析可以用来判断系统的稳定性和性能。
系统的根轨迹可以通过以下步骤进行绘制:(1)确定系统的传递函数G(s)(2)将G(s)写成标准形式(3)计算系统的极点和零点(4)绘制系统的根轨迹三、实验步骤1.系统稳态误差分析实验(1)将系统的开环传递函数和闭环传递函数写出。
(2)通过实验,测量系统的静态误差和动态误差。
(3)根据静态误差和动态误差的测量结果,计算系统的稳态误差。
2.系统阻尼比分析实验(1)通过实验,测量系统的振荡频率和衰减周期。
(2)根据振荡频率和衰减周期的测量结果,计算系统的阻尼比。
3.系统根轨迹分析实验(1)将系统的传递函数写成标准形式。
(2)计算系统的极点和零点。
(3)绘制系统的根轨迹,并根据根轨迹的形状,判断系统的稳定性和性能。
四、实验结果分析通过实验,我们可以得到系统的稳态误差、阻尼比和根轨迹等数据。
根据这些数据,我们可以分析系统的稳定性和性能,并对系统进行优化。
控制工程基础实验指导书自控原理实验室编印(内部教材)实验项目名称:(所属课程:)院 系: 专业班级: 姓 名: 学 号:实验日期: 实验地点: 合作者: 指导教师:本实验项目成绩: 教师签字: 日期:(以下为实验报告正文)一、实验目的简述本实验要达到的目的。
目的要明确,要注明属哪一类实验(验证型、设计型、综合型、创新型)。
二、实验仪器设备列出本实验要用到的主要仪器、仪表、实验材料等。
三、实验内容简述要本实验主要内容,包括实验的方案、依据的原理、采用的方法等。
四、实验步骤简述实验操作的步骤以及操作中特别注意事项。
五、实验结果给出实验过程中得到的原始实验数据或结果,并根据需要对原始实验数据或结果进行必要的分析、整理或计算,从而得出本实验最后的结论。
六、讨论分析实验中出现误差、偏差、异常现象甚至实验失败的原因,实验中自己发现了什么问题,产生了哪些疑问或想法,有什么心得或建议等等。
七、参考文献列举自己在本次准备实验、进行实验和撰写实验报告过程中用到的参考文献资料。
格式如下作者,书名(篇名),出版社(期刊名),出版日期(刊期),页码实验一 控制系统典型环节的模拟一、实验目的、掌握比例、积分、实际微分及惯性环节的模拟方法; 、通过实验熟悉各种典型环节的传递函数和动态特性; 、了解典型环节中参数的变化对输出动态特性的影响。
二、实验仪器、控制理论电子模拟实验箱一台;、超低频慢扫描数字存储示波器一台;、数字万用表一只;、各种长度联接导线。
三、实验原理以运算放大器为核心元件,由其不同的 输入网络和反馈网络组成的各种典型环节,如图 所示。
图中 和 为复数阻抗,它们都是 、 构成。
图 运放反馈连接基于图中 点为电位虚地,略去流入运放的电流,则由图 得:21()o i u ZG s u Z ==-( ) 由上式可以求得下列模拟电路组成的典型环节的传递函数及其单位阶跃响应。
、比例环节实验模拟电路见图 所示图 比例环节传递函数:21()R G s K R =-=- 阶跃输入信号: 实验参数:( ) 1 2 ( ) 1 2 、 惯性环节实验模拟电路见图 所示图 惯性环节传递函数:2212211211()11R CS R Z R K CS G s Z R R R CS TS +=-=-=-=-++阶跃输入: 实验参数:( )12( )2、积分环节实验模拟电路见图 所示图 积分环节传递函数:21111()Z CSG sZ R RCS TS=-=-=-=阶跃输入信号:实验参数:( )( )、比例微分环节实验模拟电路见图 所示图 比例微分环节传递函数:22211111()(1)(1)1D Z R R G S R CS K T S R Z R CS R CS =-=-=-+=-++ 其中 D 112R R 阶跃输入信号: 实验参数:( ) 1 2 ( ) 1 2 四、实验内容与步骤、分别画出比例、惯性、积分、比例微分环节的电子电路; 、熟悉实验设备并在实验设备上分别联接各种典型环节;、按照给定的实验参数,利用实验设备完成各种典型环节的阶跃特性测试,观察并记录其单位阶跃响应波形。
实验五线性系统的稳定性和稳态误差分析实验五 自动控制系统的稳定性和稳态误差分析一、实验目的1、研究高阶系统的稳定性,验证稳定判据的正确性;2、了解系统增益变化对系统稳定性的影响;3、观察系统结构和稳态误差之间的关系。
二、实验任务1、稳定性分析欲判断系统的稳定性,只要求出系统的闭环极点即可,而系统的闭环极点就是闭环传递函数的分母多项式的根,可以利用MATLAB 中的tf2zp 函数求出系统的零极点,或者利用root 函数求分母多项式的根来确定系统的闭环极点,从而判断系统的稳定性。
(1)已知单位负反馈控制系统的开环传递函数为0.2( 2.5)()(0.5)(0.7)(3)s G s s s s s +=+++,用MATLAB 编写程序来判断闭环系统的稳定性,并绘制闭环系统的零极点图。
在MATLAB 命令窗口写入程序代码如下: z=-2.5p=[0,-0.5,-0.7,-3] k=0.2 Go=zpk(z,p,k) Gc=feedback(Go,1) Gctf=tf(Gc) dc=Gctf.dendens=poly2str(dc{1},'s') 运行结果如下:dens=s^4 + 4.2 s^3 + 3.95 s^2 + 1.25 s + 0.5dens是系统的特征多项式,接着输入如下MATLAB程序代码:den=[1,4.2,3.95,1.25,0.5]p=roots(den)运行结果如下:p =-3.0058-1.0000-0.0971 + 0.3961i-0.0971 - 0.3961ip为特征多项式dens的根,即为系统的闭环极点,所有闭环极点都是负的实部,因此闭环系统是稳定的。
下面绘制系统的零极点图,MATLAB程序代码如下:z=-2.5p=[0,-0.5,-0.7,-3]k=0.2Go=zpk(z,p,k)Gc=feedback(Go,1)Gctf=tf(Gc)[z,p,k]=zpkdata(Gctf,'v')pzmap(Gctf)grid运行结果如下:z =-2.5000p =-3.0058-1.0000 -0.0971 + 0.3961i -0.0971 - 0.3961i k =0.2000输出零极点分布图如图3-1所示。
实验四 线性定常系统的稳态误差一、实验目的1.通过本实验,理解系统的跟踪误差与其结构、参数与输入信号的形式、幅值大小之间的关系;2.研究系统的开环增益K 对稳态误差的影响。
二、实验原理控制系统的方框图如图4-1所示。
其中G(S)为系统前向通道的传递函数,H(S)为其反馈通道的传递函数。
图4-1 控制系统的方框图由图4-1求得)()()(11)(S R S H S G S E +=(4-1)由上式可知,系统的误差E(S)不仅与其结构和参数有关,而且也与输入信号R(S)的形式和大小有关。
如果系统稳定,且误差的终值存在,则可用下列的终值定理求取系统的稳态误差:)(lim 0S SE e s ss →=(4-2)本实验就是研究系统的稳态误差与上述因素间的关系。
下面叙述0型、I 型、II 型系统对三种不同输入信号所产生的稳态误差ss e 。
1.0型二阶系统设0型二阶系统的方框图如图4-2所示。
根据式(4-2),可以计算出该系统对阶跃和斜坡输入时的稳态误差:图4-2 0型二阶系统的方框图● 单位阶跃输入(sS R 1)(=) 3112)1.01)(2.01()1.01)(2.01(lim 0=⨯+++++⨯=→S S S S S S e S ss (4-3) 输入输出响应曲线如图4-1所示,仿真图如图4-2所示。
图4-3 0型系统阶跃响应稳态误差响应曲线 图4-4 Matlab 仿真曲线由 Matlab 仿真结果来看,输入为单位阶跃信号时,输出稳态误差近似为,符合 4-3式计算的理论值。
● 单位斜坡输入(21)(s S R =) ∞=⨯+++++⨯=→2012)1.01)(2.01()1.01)(2.01(lim S S S S S S e S ss (4-4)输入输出响应曲线如图4-3所示,仿真图如图4-4所示。
图4-5 0型系统斜坡响应稳态误差响应曲线 图4-6 Matlab 仿真曲线由 Matlab 仿真结果来看,输入为单位阶跃信号时,输出稳态误差趋于无穷大,符合4-5式理论计算值。
上述结果表明0型系统只能跟踪阶跃信号, 0型系统跟踪阶跃输入有稳态误差,计算公式为:Pss K R e +=10(4-5)其中)()(lim 0S S H S G K p →≅,R 0为阶跃信号的幅值。
2.I 型二阶系统设图4-4为I 型二阶系统的方框图。
图4-7 I 型二阶系统方框图● 单位阶跃输入SS S S S S R S G S E 110)1.01()1.01()()(11)(⨯+++=+=0110)1.01()1.01(lim 0=⨯+++⨯=→SS S S S S e S ss (4-6)图4-8 I 型系统阶跃响应稳态误差响应曲线 图4-9 Matlab 仿真曲线由 Matlab 仿真结果来看,输入为单位阶跃信号时,输出稳态误差近似为0,符合4-6计算的理论值。
● 单位斜坡输入1.0110)1.01()1.01(lim 20=⨯+++⨯=→SS S S S S e S ss (4-7)图4-10 I 型系统斜坡响应稳态误差响应曲线 图4-11 Matlab 仿真曲线由 Matlab 仿真结果来看,输入为单位斜坡信号时,输出稳态误差近似为,符合4-7计算的理论值。
这表明I 型系统的输出信号完全能跟踪阶跃输入信号,在稳态时其误差为零。
对于单位斜坡信号输入,系统输出有稳态误差,,理论误差计算公式为:VOK V (4-8) 其中)()(lim 0S H S SG K S V →=,O V 为斜坡信号对时间的变化率。
3.II 型二阶系统设图4-5为II 型二阶系统的方框图。
图4-12 II 型二阶系统的方框图● 单位阶跃输入当单位阶跃输入时II 型二阶系统的仿真曲线如图4-13所示图4-13 II 型二阶系统单位阶跃输入仿真曲线结果趋于零。
● 单位斜坡输入当单位斜坡输入时II 型二阶系统的仿真曲线如图4-14所示图4-14 II 型二阶系统单位斜坡输入仿真曲线结果趋于零。
● 单位抛物输入当单位抛物波输入时II 型二阶系统的理论稳态偏差曲线如图4-15所示,仿真曲线如图图4-15 II 型系统的抛物波稳态误差响应曲线 图4-16 Matlab 仿真曲线表明II 型系统的输出信号完全能跟踪阶跃和斜坡输入信号,在稳态时其误差为零。
当输入信号为抛物波221)(t t r =,即31)(S S R =时,其稳态误差为:1.01)47.01(10lim 3220=⨯++⨯=→S s S S S e S ss (4-9)三、实验内容连接电路,在上位机上观察实验曲线。
1.0型二阶系统当输入u r 为一单位阶跃信号时,用上位软件观测图中e 点并记录其实验曲线,并与理论偏差值进行比较。
当输入u r 为一单位斜坡信号时,用上位软件观测图中e 点并记录其实验曲线,并与理论偏差值进行比较。
● 单位阶跃输入由4-17图可得,稳态误差为,与实际稳态误差较接近。
实验曲线如下图所示:图4-17 0型二阶系统单位阶跃响应曲线●单位斜坡输入由4-18图可得,稳态误差无穷大,与理论相符。
实验曲线如下图所示:图4-18 0型二阶系统单位阶跃响应曲线2.I型二阶系统当输入u r为一单位阶跃信号时,用上位软件观测图中e点并记录其实验曲线,并与理论偏差值进行比较。
当输入u r为一单位斜坡信号时,用上位软件观测图中e点并记录其实验曲线,并与理论偏差值进行比较。
●单位阶跃输入由4-19图可得,I型二阶系统在单位阶跃输入下稳态误差为零,与理论相符。
实验曲线如下图所示:图4-19 I型二阶系统单位阶跃响应曲线●单位斜坡输入由4-20图可得,I型二阶系统在单位斜坡输入下稳态误差为零,与理论相符。
试验曲线如下图所示:图4-20 I型二阶系统单位斜坡响应曲线3.II型二阶系统当输入u r为一单位斜坡(或单位阶跃)信号时,用上位软件观测图中e点并记录其实验曲线,并与理论偏差值进行比较。
当输入u r为一单位单位抛物波信号时,用上位软件观测图中e点并记录其实验曲线,并与理论偏差值进行比较。
●单位阶跃输入由4-21图可得,II型二阶系统在单位阶跃输入下稳态误差为零,与理论相符。
试验曲线如下图所示:图4-21 II型二阶系统单位阶跃响应曲线●单位斜坡输入由4-22图可得,II型二阶系统在单位斜坡输入下稳态误差为零,与理论相符。
试验曲线如下图所示:图4-22 II型二阶系统单位斜坡响应曲线●单位抛物波输入由4-23图可得,I型二阶系统在单位抛物波输入下稳态误差近似为,与理论相符。
试验曲线如下图所示:图4-23 II 型二阶系统单位抛物波响应曲线四、实验思考题1. 为什么0型系统不能跟踪斜坡输入信号? 答: 以实验要求中给出的系统为例,图4-24 0型二阶系统的方框图从0型系统的方框图可以推知,对阶跃信号稳态误差为3112)1.01)(2.01()1.01)(2.01(lim 0=⨯+++++⨯=→S S S S S S e S ss对斜坡信号的稳态误差为∞=⨯+++++⨯=→2012)1.01)(2.01()1.01)(2.01(lim S S S S S S e S ss可见,由于0型系统的E(S)在原点处没有零点,而斜坡信号拉氏变换后在原点有一个二阶极点,极点不能被抵消,造成了误差的不断累积,因此0型系统不能跟踪斜坡输入信号。
2. 为什么0型系统在阶跃信号输入时一定有误差存在,决定误差的因素有哪些?答:同样以以实验要求中给出的系统为例,从0型系统的方框图可以推知,对阶跃信号稳态误差为:3112)1.01)(2.01()1.01)(2.01(lim 0=⨯+++++⨯=→S S S S S S e S ss可见,由于阶跃信号拉氏变换后在原点只有一个一阶极点,能够被抵消,同时也不存在未被抵消的零点,这时的就是常数。
从系统框图可见,0型系统由两个惯性环节串联,再做负反馈构成,惯性环节的传递函数:稳态误差决定于两个惯性环节的放大倍数。
3. 为使系统的稳态误差减小,系统的开环增益应取大些还是小些?答:从上面的计算式子就可以看出,为了减少0型系统的稳态误差,系统的开环增益应当取大些。
对于I 型系统,前面也已推导过,对斜坡信号输入存在稳态误差,其值为VO K V ,其中)()(lim 0S H S SG K S V →=,O V 为斜坡信号对时间的变化率。
对于II 型系统,情况类似,可见,为了减少稳态误差,开环增益都应该增大。
五、心得体会此次实验有让我增长了许多知识,在学习理论知识的同时锻炼;了自己的动手能力,在实验过程中遇到了很多问题,包括THKKL-6型试验仪的接线问题,上位机的调试问题,然后通过仔细的阅读使用说明书并细心检查线路后,排除了相应的困难,在不断的解决问题的过程中逐步提升自己的实践动手能力以及对知识的熟悉掌握程度。
这次实验加深了我对线性系统稳态误差的理解,通过实物模拟学习到了0型、I 型、II 型二阶系统跟踪阶跃等信号的稳态误差,让我对自动控制这门学科的奇妙之处颇为惊讶,同时激发了我继续探索控制领域其他理论知识的兴趣,这些经验对我们以后的学习将有着一定的帮助与启示,使我们对自己的专业和以后将从事的工作拥有更加全面的了解和认识。