当前位置：文档之家 › 系统稳态误差的计算

系统稳态误差的计算

  • 格式：ppt
  • 大小：609.00 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

系统的稳态误差为

系统的稳态误差为


r (t ) t
e ss
1
r (t ) t
e ss
1
2
Kp
0型 I型 II型
Kv
0
Ka
0 0
ess
1
1
2
1 K
K
p
KvKp1来自 1Ka
K
0 0
Kv
K
0
Ka
三、系统稳定误差的计算


综述，系统的稳态误差与输入信号形式有 关，对于一个结构确定的系统，如果给定 输入形式不同，其稳态误差就不同；同时 稳态误差与系统结构也密切相关，如果给 定信号一定，不同结构的系统稳态误差也 不同。 按静态误差系数法计算稳态误差的方法， 是基于拉氏变换的终值定理，只能使用阶 跃、斜坡及加速度或他们的组合，如果输 入是其他任意时间函数，以上结论则不能 成立。
ess
特征方程为D( s) 1 Gk ( s) an s n an 1s n 1 ... a2 s 2 a1s a0 0
n n 1 2 a s a s ... a s 等式两边同除以 n n 1 2 a1s a0 1 Gk ( s) 0 1 0 则 n n 1 2 an s an 1s ... a2 s 得 a1s a0 Gk ( s) 该系统为Ⅱ型系统 an s n an 1s n 1 ... a2 s 2 开环增益为 a0 a1s a0 K 2 a2 n2 n 3 s (an s an 1s ... a2 )
ess
1、先求取系统的开环传递函数 Gk ( s)
Gk (s)
C(s)
设开环传递函数为 Gk ( s) M ( s) 即，开环传递函数 N ( s) 与闭环传递函数 M (s) 有相同的零点 Gk ( s ) M (s) N (s) GB ( s ) a s a0 1 Gk ( s ) 1 M ( s ) N ( s ) M ( s ) 得 Gk ( s ) 1 ? N (s)
稳态误差的计算_图文(精)

稳态误差的计算_图文(精)


ess 与输入和开环传递函数有关。 显然， 假设开环传递函数 Gk (s) 的形式如下：
K Gk ( s ) s
2 ( s 1 ) ( s i k 2 k k s 1) 2 ( T s 1 ) ( T s j l 2 lTl s 1) j 1 l 1 i 1 n1 k 1 n2 m1 m2
R(s)
E ' (s) E (s) H (s)
E’(s) 1/H(s)
N(s)
C(s)
e(t)
E(s)
+
B(s)
式中： r(t)为给定输入； 图 典型反馈系统结构图 b(t)为系统主反馈信号。 H （ s ）是测量装置的传递函数（通常我们认为是理想的）， 故此时误差就是给定输入与测量装置的输出量之差。 误差的定义
s 0
当 0时，K v lim sKG0 ( s ) 0 ,
s 0
当 1时，K v lim KG0 ( s ) K , s 0 K 当 2时，K v lim G0 ( s) , s 0 s 结论：
0型系统稳态时不能跟踪斜坡输入
ess 1 ess K ess 0
单位阶跃函数输入时的稳态误差
1 当输入为 R ( s ) 时（单位阶跃函数） s sR(s) 1 1 1 ess lim s 0 1 G ( s) 1 lim Gk (s) 1 lim K G (s) 1 K p k s 0 0 s 0 s 式中：K p lim Gk ( s ) 称为位置误差系数； s 0 1 当 0时，K p lim KG0 ( s ) K , ess s 0 1 K K 当 1时，K p lim G0 ( s ) , ess 0 s 0 s K p 的大小反映了系统在阶跃输入下的稳态精度。 K p 越大，ess 越 小。所以说 K p 反映了系统跟踪阶跃输入的能力。
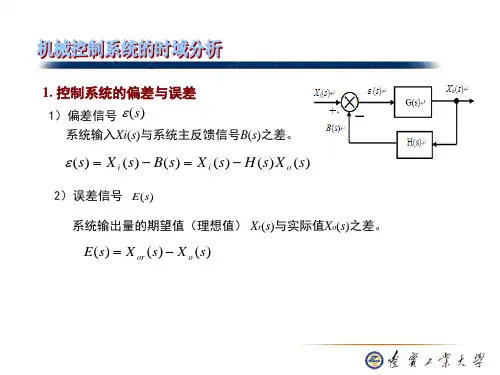
系统稳态误差的计算

系统稳态误差的计算

显然，系统稳态偏差(误差)决定于输入 X i (s) 和开环传递函数Gk (s) G(s) H (s) 即决定于输入信号的特性及系统的结构和参数。
4.典型输入信号的稳态误差及静态误差系数
设开环传递函数的一般形式为：
G( s) H ( s)
k ( 1 s 1)( 2 s 1)...( m s 1) s (T1 s 1)(T2 s 1)....( Tn s 1)
5. 扰动引起的稳态误差
图示系统，扰动偏差传递函数为： n ( s) G2 (s) H (s) N (s) 1 G1 (s)G2 (s) H (s) 所以，扰动引起的稳态偏差：
ssn lim s n (s) lim s
s 0 s 0
G2 (s) H (s) G2 ( s ) H ( s ) N (s) lim s N ( s) s 0 1 G1 (s)G2 (s) H (s) 1 GK ( s)
系统在多个信号共同作用下总的稳态偏差误差等于多个信号单独作用下的稳态偏差误差之和
1. 控制系统的偏差与误差 1）偏差信号 ( s)
系统输入Xi(s)与系统主反馈信号B(s)之差。
(s) X i (s) B(s) X i (s) H (s) X o (s)
2）误差信号 E ( s )
2. 稳态误差
ess 与稳态偏差 ss
s 0
1）稳态误差
e ss lim e(t ) lim sE ( s )
t
2）稳态偏差
ss lim (t ) lim s ( s )
t s 0
。
3）稳态误差与稳态偏差的关系：
ss s ( s) ess lim e(t ) lim sE ( s) lim t s 0 s 0 H ( s ) H (0)
3-7 线性系统的稳态误差计算

3-7 线性系统的稳态误差计算


！ 系统类型(type)与系统的阶数(order)的区别
m
令
( i s 1)
G0(s)H0(s)
i 1 n
(j s 1)
j 1
m
K (is 1)
G(s)H (s)
i 1 n
s (js 1)
j 1
当 S 0,G0 (s)H0 (s) 1
G(s)H (s)
K s
G0 (s)H0 (s)
s0
sE(s)
lim
s0
1
G1(s)G2 (s)H (s)
公式条件：
结构形式 开环传递函数
sE(s) 的极点均位于S左半平面（包括坐标原点）
给定的稳定系统，当输入信号形式一定时，系统是否存 在稳态误差，就取决于开环传递函数所描述的系统结构
按照控制系统跟踪不同输入信号的能力来进行系统分类是必要的
Type
(t) cr (t) c(t) r(t) c(t) e(t) ss ess
对非单位反馈系统：
给定作用 r(t)只是希望输出的代表，r(t) cr (t) ，
偏差不等于误差 ss ess 。可以证明两者之间存在一
定的关系：
E(s) R(s) B(s) H(s)Cr (s) H(s)C(s) H(s) (s)
const
0
0 1
可见，由于0型系统中没有积分环节，它对阶跃输入
的稳态误差为一定值，误差的大小与系统的开环放大
系数K成反比，K越大，K越小，只要K不是无穷大，
系统总有误差存在。
对实际系统来说，通常是允许存在稳态误差的，但
不允许超过规定的指标。为了降低稳态误差，可在稳
定条件允许的前提下，增大系统的开环放大系数，若
3.7 控制系统的稳态误差

3.7 控制系统的稳态误差


一、误差与稳态误差
R(s) E(s)
C(s)
G(s)

： ⑴从输入端定义：
系统偏差：系统的输入r (t) 和主反馈信号b (t)之差。
e(t) r(t) b(t)
⑵从输出端定义： 系统误差：输出量的希望值c’(t)与实际值c(t) 之差。
表示系统稳态误差
二、稳态误差的计算式
系统框图 给定作用下的偏差传递函数
误差的时域计算式：
采用拉氏变换终值定理计算稳态误差 (使用条件：
sE(s)的极点均在左半平面，包括原点)
3．8 稳态误差分析与计算
一、给定输入作用下系统的误差分析 1．系统型别 系统开环传递函数:GK(s)=G(s) H(s) 假设开环传递函数GK(s)的形式如下：
Ci 称为动态误差系数，Ci怎么得到？
⑴对
,在s=0的邻域内展开为泰勒级数。
⑵ 对 ,分子多项式除以分母多项式，商为：
① 0型系统 GK(s)=G(s) H(s)
给定有静差系统
②Ⅰ型系统
③Ⅱ型系统
给定无静差系统
给定无静差系统
⑵ 单位斜坡输人 ① 0型系统
大误差
②Ⅰ型系统
给定有静差
③Ⅱ型系统
给定无静差
⑶ 单位抛物线输人 ① 0型系统
大误差
②Ⅰ型系统
大误差
③Ⅱ型系统
有给定静差
无差系统：在阶跃函数作用下没有原理性稳态误差的系统。 有差系统：在阶跃函数作用下具有原理性稳态误差的系统。
式中，K：为系统的开环增益
v可称为系统无差度 ，表示系统的型别 由公式
可看出，稳态误差 ess与输入和开环传递函数型别有关。 v可称为系统无差度
2．静态误差系数 定义:
线性系统的稳态误差计算

线性系统的稳态误差计算

函数为
G( s) K S ( S 2 bS C )
p 1 p 2 b C 4 2 p 2 C 2 p K 0.5C K 2 b 3
因为 ess 按定义
1 2 Kr
s 0
Kv
K 0.5, K 0.5C C
令r (t ) Rt 2 / 2，R 常量，R(s) R / s3。
sR(s) sR / s3 R R R ess lim lim lim 2 2 lim 2 s 0 1 G( s) H ( s ) s 0 1 G( s ) H ( s ) s 0 s s G ( s ) H (s ) s 0 s G (s ) H (s ) Ka
系统稳态误差计算通式则可表示为
ess
1 lim s R ( s )
s 0
sR( s) ess lim sE ( s) lim s 0 s 0 1 G ( s ) H ( s )
K lim s
s 0
系统型别 e ss 与 K 开环增益有关 R ( s ) 输入信号
def
E ( s) 1 R(s) 1 H ( s)G( s)
E ( s ) e ( s ) R( s ) R( s ) 1 H ( s)G( s)
e(t ) L1[e (s)R(s)] ets (t ) ess (t )
瞬态分量
稳态分量
E ( s ) e ( s ) R( s )
要求对于阶跃作用下不存 在稳态误差，则必须选用 Ⅰ型及Ⅰ型以上的系统
4.斜坡输入作用下的稳态误差和静态速度误差系数
r (t ) Rt，R 常量，R(s) R / s 2。
3-6线性系统的稳态误差计算

3-6线性系统的稳态误差计算

i=1 n 1 i k =1 n2 k j =1 j l =1 l
m 1
m2
2
+ 2ζ kτk s +1) + 2ζlTs +1) l
∏(T s +1)∏(Ts
=
2
K ⋅ G0 (s) sν
sR(s) 1 essr = lim = = s→0 1+ G (s) 1+ limGk (s) k
s→0
1 1 = K 1+ Kp 1+ lim ν ⋅ G0 (s) s→0 s
三、扰动作用下的稳态误差(3) 扰动作用下的稳态误差(3) [例]系统结构图如图所示。当 r(t) = n(t) = 1(t) 系统结构图如图所示。 时，求系统的稳态误差 ess；若要求稳态误差 为零，如何改变系统结构。 为零，如何改变系统结构。 解：该系统对给定输入而言属于Ⅰ型系统。 该系统对给定输入而言属于Ⅰ型系统。 所以当给定输入为单位阶跃函数时的稳态误差 essr = 0
3、单位抛物线输入时的稳态误差
R(s) =
1 s3
sR(s) 1 essr = lim = = 2 s→0 1+ G (s) lims ⋅ Gk (s) k
s→0
1 1 = K Ka lim ν −2 ⋅ G0 (s) s→0 s
∞ 1 = K 0
Ka
根据
ν =0,1 ν =2 ν ≥3
m2
=
K ⋅ G0 (s) ν s
K－开环增益
系统型别（即积分环节的个数） ν − 系统型别（即积分环节的个数）
当ν =0，无积分环节，称为0型系统 无积分环节，称为0
当 = ，有一个积分环节，称为Ⅰ型系统 ν 1 有一个积分环节，称为Ⅰ
3.6 线性系统的稳态误差计算

3.6 线性系统的稳态误差计算

3-6 线性系统稳态误差计算
稳态误差是系统的稳态性能指标，是系 统控制精度的度量。 计算系统的稳态误差以系统稳定为前提 条件。
一、误差与稳态误差 1、从输入端定义误差： 给定量与主反馈量之差
E ( s) R( s) H ( s)C ( s)
R(s)
E(s)
(-) B(s)
G(s) H(s)
Ⅰ型系统，在R(s)作用下稳态误 差为0
n0 G2 ( s) K2 N (s) 1 G1 ( s)G2 ( s) s(T2 s 1) K1K 2 s
K 2 n0 n0 lim sEn (s ) lim s 0 s 0 s (T s 1) K K K1 2 1 2
C(s)
可测量 误差的理论含义不明显
R(s) Cr (s) E’(s) 1/H(s) (-) E(s) C(s) G(s)
2、从输出端定义误差： 输出量希望值与实际值之差
R( s ) ( s) E C ( s) H ( s)
H(s)
不可测量 较接近e(t )的含义
E( s ) H ( s ) E( s )
例题 设单位负反馈系统开环传递函数为G(s)=1/Ts , 输入信号分别 为 1）r(t)=t ，2) r(t)=t2/2，3) r(t)=sinωt，求系统稳态误差。 解：误差传递函数为 e ( s)
E ( s) 1 Ts , 系统稳定 R( s) 1 G( s) H ( s) 1 Ts
5 s(5s 1)
0.8s
C(s)
解：开环传递函数为 闭环传递函数为： ( s)
5 1 s (5 s 1) G (s) 5s s ( s 1) 1 0 .8 s (5 s 1)
3.3线性系统的稳态误差计算

3.3线性系统的稳态误差计算


e ss
本 书 第 8 章 介 绍
稳态误差的不可避免性
摩擦，不灵敏区，零位输出等非线性因素
输入函数的形式不同 (阶跃、斜坡、或加速度)
无差系统： 在阶跃函数作用下没有原理性稳态误差的系统。 有差系统： 在阶跃函数作用下具有原理性稳态误差的系统。
本节主要讨论
系统结构--系统类型 输入作用方式
原理性稳态误差的计算方法
def
E (s) R(s) H (s)C (s)
E ( s) 1 R( s ) 1 H ( s)G ( s)
E ( s ) e ( s ) R( s ) R( s ) 1 H ( s)G ( s)
e(t ) L1[ e ( s) R( s)] ets (t ) ess (t )
sR( s ) sR / s 2 R R R ess lim lim lim lim s 0 1 G ( s ) H ( s ) s 0 1 G ( s ) H ( s ) s 0 s sG ( s ) H ( s ) s 0 sG ( s ) H ( s ) Kv
1 r (t ) R0 1(t ) R1t R2t 2 2
R0 R1 R2 ess 1 K p K v Ra
例：I型单位反馈系统的开环增益K=600s-1，系统 最大跟踪速度max =24/s，求系统在最大跟踪 速度下的稳态误差。
1 解：单位速度输入下的稳态误差 ess Kv I型系统 K v K
系统的稳态误差为
1 1 ess max 24 0.04 Kv 600
例：阀控油缸伺服工作台要求定位精度为0.05cm, 该工作台最大移动速度vmax =10cm/s，若系统 为I型，试求系统开环增益。
稳态误差计算(普通解法)

稳态误差计算(普通解法)


⎡ K ⎤ 1 ⎤ ⎡1 G( z) = Z ⎢ = KZ ⎢ − ⎥ ⎣ s s + 1⎥ ⎦ ⎣ s ( s + 1) ⎦
z ⎛ z =K⎜ − −T ⎝ z −1 z − e
系统特征方程为
图 6-21 离散系统结构图
K (1 − e−T ) z ⎞ = ⎟ −T ⎠ ( z − 1)( z − e )
D( z ) = ( z − 1)( z − e −T ) + K (1 − e −T ) z = z 2 + [(1 − e −T ) K − 1 − e −T ]z + e −T = 0
利用朱利稳定判据
⎧ D(1) = K (1 − e −T ) > 0 ⎪ ⎨ −T −T ⎪ ⎩ D(−1) = 2(1 + e ) − K (1 − e ) > 0
e(∞) = lim
z →1
( z − 1)( z − 0.368) =0 z 2 − 0.736 z + 0.368
2
当 r (t ) = t ，相应 r (nT ) = nT 时， R ( z ) = T z ( z − 1) ，于是由式(6-59)求得
e(∞) = lim
z →1
T ( z − 0.368) = T =1 z − 0.736 z + 0.368
G( z) =
e − T z + 1 − 2e − T 0.368 z + 0.264 = 2 −T ( z − 1)( z − e ) T =1 z − 1.368 z + 0.368
2
0.368 z + 0.264 →∞ z − 1.368 z + 0.368 0.368 z + 0.264 =1 K v = lim( z − 1) 2 z →1 z − 1.368 z + 0.368 K p = lim
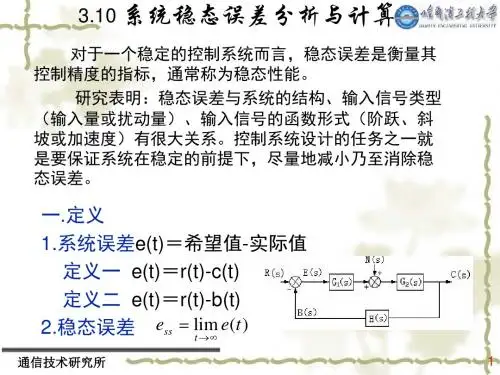
自动控制原理_第3章2

自动控制原理_第3章2


令Gc (s)
通信技术研究所
G f ( s) G( s)
, 得C (s) G( s) R( s) C ( s)
13
<例3-15>r(t)=1,n(t)=1 ,求ess
通信技术研究所
14
1 2 <例3-16> r (t ) 1 t t ,求ess 2 注：E=R-C
K (1s 1)( 2 s 1) ( m s 1) 1 K , ess （1） 0, K p lim 0 1 K s 0 s (T 1s 1)(T2 s 1) (T j s 1)
s 0
s
K (1s 1)( 2 s 1) ( m s 1) , ess 0 （2） 1, K p lim 1 s 0 s (T 1s 1)(T2 s 1) (T j s 1) K (1s 1)( 2 s 1) ( m s 1) 2, K p lim 2 , ess 0 （ 3） s 0 s (T 1s 1)(T2 s 1) (T j s 1)
s
K (1s 1)( 2 s 1) ( m s 1) 0, Kv lims 0 0, ess （ 1） s (T1s 1)(T2 s 1) (T j s 1) s 0 K (1s 1)( 2 s 1) ( m s 1) 1 K , ess （2） 1, Kv lims 1 s (T1s 1)(T2 s 1) (Tj s 1) K s 0 K (1s 1)( 2 s 1) ( m s 1) （3） 2, Kv lims 2 , ess 0 s (T1s 1)(T2 s 1) (T j s 1) s 0

3.5 控制系统的稳态误差分析与计算终


2.系统的类型
K 1s 1 2 s 1 Gk s Gs H s v s T1s 1T2 s 1
K为开环增益 τ1、τ2……和T1、T2……为时间常数
n m
1、系统对单位阶跃输入的稳态偏差 K 1s 11 2 s 1 s lim G G sE H s n m s s lim X s k v s ss i s 0 s s0 T1 s G 1 T s 1 1 s2 H s
s s Gk s
K 1s 1 对0型系统 K a lim s 0 s 0 T1s 1 1s 1 2 K 对I型系统 K a lim s 0 s 0 sT1s 1 1s 1 2 K
2
稳态加速度偏差系数 令：K
a
ss s 0 s 0 i s 0 k
2
K 1s 1 对0型系统 K v lim s 0 ss s 0 T1s 1 K 1s 1 1 对I型系统 K v lim s K ss s 0 sT1s 1 K K 1s 1 对II型系统 K v lim s 0 ss 2 s 0 s T1s 1
lim s Gs H s lim s Gk s
2 2 s 0 s 0
ss
ss
1 ss K
对II型系统 K a lim s s 0
s T1s 1
2
K
1t
t
1 ss Kv
Kv 0
K p lim Gk s K v lim sGk s K a lim s 2Gk s s 0 s 0 s 0
2 i
s H s s 1 Gs H s 1 G s T s 1T s1

《自动控制原理》第三章-3-5-稳态误差计算


伺服电动机
R(s)
E(s)
1
C(s)
-
s(s 1)
K 1, 1
r(t) 1(t),k p , ess 0
r(t) t, kv 1, ess 1
r(t)
1 2
t2, ka
0, ess
位置随动系统
能源与动力学院 第三章 线性系统的时域分析法
14
4.扰动作用下稳态误差
R(s)
-
E(s)
R(s) E(s) 20
s4
N (s)
+
2
C(s)
s(s 2)
能源与动力学院 第三章 线性系统的时域分析法
28
3-20
R
-
K1
U
K2 S(T1S 1)
C
G(s)
K1K 2
B
s(T1s 1)(T2s 1)
1 T2S 1
(s)
C(s) R(s)
T1T2 s 3
K1K2 (T2s 1) (T1 T2 )s2 s
1
能源与动力学院 第三章 线性系统的时域分析法
7
3.输入作用下稳态误差计算
（1）阶跃作用下的稳态误差
r(t) R 1(t), R(s) R s
ess
Lim sR(s) s0 1 G(s)H (s)
Lim s1R(s)
s0
K Lim s
s0
1
R LimG(s)H (s)
Lim s R
s0
K Lim s
27
参考答案: Kp= ,kv=5,ka=0,essr=0.4，essn=-0.2
四、控制系统如图, r(t) 1 2t, n(t) 1(t), 试计算

§3-5稳态误差的分析与计算

R(s) H1(s) G1(s) N(s) G2(s) C(S)
G 2 (s) E n (s) Cn (s) N(s) 1 G1 (s)G 2 (s)H(s)
s 0
s 0
给定输入下的稳态误差与稳态误差系数
1 e ssr 阶跃输入下: 1 KP 斜坡输入下: essr 1 Kv 1 e ssr 抛物线输入下: Ka
K (TjS 1) G (s) S (TiS 1)
i 1 j1 n
K G( s) v s
i 1
n
系统开环传递函数中 不含积分环节
KP lim G (s) K
s 0
e ss 1 1 K
阶跃输入时，误差系数=K
输出始终不会等于输入，存在稳态误差
K lim SG (s) 0 斜坡输入时，误差系数=0 s 0
ess
2

稳态误差无穷大（输出不能跟随输入）
Ka lim S G (s) 0抛物线输入时，误差系数=0 s 0 ess 输出不能跟随输入，
KP lim G(s)
K lim SG(s)
s 0
s 0
Ka lim S G(s)
s 0
m2
2
m
( s 1) (
i i 1 n1 k 1 n2 j j 1 l 1
m1
2 2 k
s 2 k k s 1) s 2 l l s 1)
(T s 1) (T
2 2
l
稳态误差系数仅与系统参数K、(积分环节个数—系统 型号)有关，对应＝0、1、2 称 0、I、Ⅱ型系统
0、I、Ⅱ型三种系统 分别三种典型输入 稳态误差有九种情况

已知闭环传递函数求稳态误差

已知闭环传递函数求稳态误差已知闭环传递函数求稳态误差1. 引言在控制系统理论中，闭环传递函数是一个非常重要的概念。

其描述了控制系统在反馈作用下的动态特性，对于系统的稳定性和性能有着至关重要的影响。

而稳态误差则是评价系统性能的重要指标之一，通过已知闭环传递函数求稳态误差，可以帮助我们更好地评估和优化控制系统的性能。

2. 已知闭环传递函数的稳态误差求解当我们已知系统的闭环传递函数时，可以通过以下步骤来求解系统的稳态误差。

2.1 我们需要确定系统的类型。

系统的类型可以通过观察传递函数的分母阶数来确定，一般而言，系统类型等于传递函数的分母阶数减去传递函数的分子阶数。

在控制系统中，常见的类型包括类型0、类型1和类型2。

2.2 接下来，根据系统的类型，我们可以利用稳态误差的公式来计算系统的稳态误差。

对于类型0系统，其稳态误差可以通过以下公式来计算：\[ e_{ss} = \lim_{s \to 0} sR(s) \frac{1}{1+G(s)H(s)} \]其中，\( R(s) \) 为系统的输入信号，\( G(s) \) 为系统的开环传递函数，\( H(s) \) 为系统的反馈传递函数。

而对于类型1系统和类型2系统，其稳态误差的计算公式分别为：\[ e_{ss} = \lim_{s \to 0} (1+\frac{1}{G(s)H(s)})R(s)\frac{1}{1+G(s)H(s)} \]\[ e_{ss} = \lim_{s \to 0} \frac{1}{G(s)H(s)}R(s) \frac{1}{1+G(s)H(s)} \]3. 实例分析假设我们有一个闭环传递函数为：\[ G(s) = \frac{K}{s(s+1)(s+2)} \]其中，\( K \) 为系统的增益。

根据该传递函数，我们可以确定系统的类型为类型1，因为传递函数的分母阶数为3，分子阶数为1，所以系统类型为3-1=2。

接下来，我们可以利用稳态误差的公式来计算系统的稳态误差。

第三章(4)系统的稳态误差


K2 H G2H s K 2H s NE ( S ) 1 K 1K 2 1 G1G 2 H s K 1K 2 H 1 1 H s
干扰作用下的稳态误差
K 2 e ssn lim s NE ( s) N ( s) lim s N (s) s 0 s 0 s G K 1 2 s K 2 H lim s 1 N ( s) s 0 s K 1K 2 H
1
ess () ess lim e(t ) lim sE ( s)
t s 0
N (S )
R(S )
E (S )
G1（S）
G2(S）
C (S )
H（S）
3、系统的稳态误差：
1）设N（S）=0， 以R为输入，E为输出
1 RE ( S ) 1 G1G 2 H
2）设R（S）=0，以N为输入，E为输出
系统稳态误差计算通式则可表示为：
ess
lim[ S 1 R( s)]
s 0
K lim S
s 0

(3 64)
稳态误差与哪些因素有关？
系统型别 e ss 与 K 开环增益有关 R ( s ) 输入信号
1、阶跃信号输入 令
R0 r (t ) R0 , R0 常量。R(s) . S
二、稳态误差的计算
e(t ), lim sE ( s ) 存在，可利用终值定理 如果 lim t s 0 输入形 求稳态误差。
式
sR( s) ess () ess lim sE ( s) lim s 0 s 0 1 H ( s )G ( s )
结构形式
公式条件： sE (s) 的极点均位于S左半平面.

西工大、西交大自动控制原理 第六节 线性系统的稳态误差计算11-12


G2 s Cs
e
s
BERsss
1
1
GH1 ssG2
s
H
s
ef
s
Es F s
1
G2 sH s G1sG2 sH
s
1. 误差与稳态误差
稳态误差的计算
第六节 线性系统的稳态误差计算
Es Er s E f s e sRs ef sF s
1
G1
s
1
G2
s
H
s
Rs
1
G2 sH s G1sG2 sH
；e() R / K
▪ 对Ⅲ型以上系统v 3 ，K a ；e() 0
第六节 线性系统的稳态误差计算
2.用静态误差系数法求稳态误差
系 静态误差 阶跃输入 斜坡输入
统 系数 型 别
R 1t Rt
位置误差 速度误差
K
p
Kv
Ka
ess
R
(1 K p )
ess
R Kv
0K 00 R
1 K
Ⅰ K0 0
2.用静态误差系数法求稳态误差
静态加速度误差系数 K a
定义： Ka
lim
s0
s
2GK
s
lim
s0
s
2Gk
0
s
lim
s0
K sv2
e R R
lim
s0
K s 2
Ka
“加速度误差”
▪ ▪ ▪
对0型系统 对Ⅰ型系统 对Ⅱ型系统
v0
v 1 v2
，，K, KKaaa
0
0 K
；e() ；e()
第六节 线性系统的稳态误差计算
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

式中，为积分环节的个数 。 λ = 0, 1, 2, …时，系统分别称为0型、I型、Ⅱ型、…系统。
(1) 单位阶跃信号输入时的稳态误差及稳态位置误差系数
1 1 1 1 1 X i (s) lim s 0 H ( s ) 1 G( s ) H ( s) s 0 H ( s ) 1 G( s) H ( s ) 1 K p k 其中，K p lim G ( s ) H ( s ) G (0) H (0) lim ，称为稳态位置误差系数。 s 0 s 0 s 1 零型系统： K p k ,
5. 扰动引起的稳态误差
图示系统，扰动偏差传递函数为： n ( s) G2 (s) H (s) N (s) 1 G1 (s)G2 (s) H (s) 所以，扰动引起的稳态偏差：
从而有：
( s)
1 X i ( s) 1 G(s) H (s)
输入引起的稳态误差为： s ( s) ess lim sE( s) lim s 0 s 0 H ( s ) 1 1 1 1 ess lim s X i (s) lim s X i ( s) s 0 1 G ( s ) H ( s ) H ( S ) s 0 1 G K ( s ) H (S )
ss
1 Ka
说明：
1.如果输入量非单位量时，其稳态偏差（误差）按比例增加。 2.系统的稳态误差与其开环增益有关，开环增益越大，稳态误差越小。 3.系统在多个信号共同作用下总的稳态偏差（误差）等于多个信号单独作用下的 稳态偏差（误差）之和。 4.稳态误差系数只对相应的阶跃、速度及加速度输入有意义。
3）误差与偏差的关系
( s) X i ( s) H ( s) X o ( s)
偏差等于零的输出就是理想输出。 由
(s) X i (s) H (s) X or (s) 0
X i ( s) X or ( s) H ( s)
得：
由误差定义，得：
X i ( s) 1 E ( s) X or (s) X o (s) X o ( s) ( X i ( s) H (s) X o (s)) H ( s) H ( s)
所以：
E ( s)
( s)
H ( s)
2. 稳态误差
ess 与稳态偏差 ss
s 0
1）稳态误差
e ss lim e(t ) lim sE ( s )
t
2）稳态偏差
ss lim (t ) lim s ( s )
t s 0
。
Hale Waihona Puke 3）稳态误差与稳态偏差的关系：
K a lim s 2 G ( s) H ( s) lim 其中，
s 0 s 0
k s 2
，称为稳态加速度误差系数。
零型和Ⅰ型系统：K 0, ss a 1 Ⅱ型系统： K a k , ss k 1 1 e 稳态误差： ss H (0) K a
对于单位反馈系统，ess
(2)单位速度输入时系统的稳态误差及稳态速度误差系数
xi (t ) t 1(t ),
ss lim s
s 0
X i ( s)
1 。则稳态偏差为： s2
1 1 1 1 1 X i ( s) lim s 0 H ( s ) s sG ( s ) H ( s ) H ( s) 1 G( s) H ( s) Kv
1 Kv
对于单位反馈系统， ess ss
(3) 单位加速度输入时系统的稳态误差及稳态加速度误差系数 1 1 xi (t ) t 2 1(t ), X i (s) 。则稳态偏差为： 2 s3 1 1 1 1 1 ss lim s X i ( s) lim s 0 s 0 H ( s ) s 2 s 2G ( s ) H ( s ) H ( s) 1 G( s) H ( s) Ka
其中，K v lim sG ( s ) H ( s ) lim
s 0 s 0
k s
1
，称为稳态速度误差系数。
零型系统：
K v 0, ss
Ⅰ型系统： K v k , ss
Ⅱ型系统： K v , ss 0
稳态误差： ess
1 k
1 1 H (0) K v
显然，系统稳态偏差(误差)决定于输入 X i (s) 和开环传递函数Gk (s) G(s) H (s) 即决定于输入信号的特性及系统的结构和参数。
4.典型输入信号的稳态误差及静态误差系数
设开环传递函数的一般形式为：
G( s) H ( s)
k ( 1 s 1)( 2 s 1)...( m s 1) s (T1 s 1)(T2 s 1)....( Tn s 1)
ss s ( s) ess lim e(t ) lim sE ( s) lim t s 0 s 0 H ( s ) H (0)
ess ss 对单位反馈系统：
3. 输入引起的稳态误差计算
系统在输入作用下的偏差传递函数为：
( s)
X i ( s)

1 1 G( s) H ( s)
xi (t ) 1(t ) ， X i ( s ) 1 。则稳态偏差为： s
ss lim s
ss
Ⅰ、Ⅱ型系统： K p , 易知，稳态误差： ess
ss
1 k ss 0

H (0)
1 1 H (0) 1 K p
ess ss 对于单位反馈系统，
1 1 K p
1. 控制系统的偏差与误差 1）偏差信号 ( s)
系统输入Xi(s)与系统主反馈信号B(s)之差。
(s) X i (s) B(s) X i (s) H (s) X o (s)
2）误差信号 E ( s )
系统输出量的期望值（理想值） Xr(s)与实际值Xo(s)之差。
E(s) X or (s) X o (s)