第2章 7.第2课时 二次根式的运算

第2课时二次根式的化简1．掌握积的算术平方根的性质，并会根据性质把二次根式化简；(重点) 2．理解最简二次根式的概念，并会把二次根式化为最简二次根式．(重点，难点)一、情境导入计算：(1)4×9，4×9；(2)16×25，16×25.观察计算结果，上述每组式子计算结果有什么关系？由此你能猜想什么结论成立？二、合作探究探究点一：积的算术平方根的性质【类型一】利用积的算术平方根的性质进行二次根式计算或化简化简：(1)196×0.25；(2)（－19）×（－6481）；(3)225a6b2(a≥0，b≥0)．解析：利用积的算术平方根的性质，把它们化为几个二次根式的积，(2)小题中先确定符号．解：(1)196×0.25＝196×0.25＝14×0.5＝7；(2)（－19）×（－6481）＝19×6481＝19×6481＝13×89＝827； (3)225a 6b 2＝225·a 6·b 2＝15a 3b .方法总结：利用积的算术平方根的性质进行计算或化简，其实质就是把被开方数中的完全平方数或偶次方开出来，要注意的是，如果被开方数是几个负数的积，先要把符号进行转化，如(2)小题．【类型二】 利用积的算术平方根的性质确定字母的取值范围若a 2－a 3＝a 1－a 成立，则a 的取值范围是( )A ．a ≥0B ．a ＞0C ．a ≥1D ．0≤a ≤1 解析：a 2－a 3＝a 2（1－a ）＝a 2·1－a ＝|a |·1－a ，又a 2－a 3＝a 1－a ，所以⎩⎨⎧a ≥0，1－a ≥0.解得0≤a ≤1，故选D. 方法总结：利用积的算术平方根的性质确定字母的取值范围时，根据积的算术平方根的性质得出的每一个因式(包括被开方数)都是非负数，再列不等式(组)求解．【类型三】 逆用积的算术平方根的性质比较大小比较大小：35与5 3.解析：把根号外的因式移到根号内，比较两个被开方数的大小．解：∵35＝32×5＝45，53＝52×3＝75，∵75＞45，∴35＜5 3.方法总结：比较两个二次根式的大小，可以逆用积的算术平方根的性质，把根号外的因式移到根号内，直接比较两个被开方数的大小，对于两个正数，被开方数大的数较大．探究点二：最简二次根式【类型一】最简二次根式的判定下列二次根式中，最简二次根式是( ) A.8a B.3aC.a3D.a2＋a2b解析：A选项中8a含能开得尽方的因数4，不是最简二次根式；B选项是最简二次根式；C选项a3中含有分母，不是最简二次根式；D选项a2＋a2b中被开方数用提公因式法因式分解后得：a2＋a2b＝a2(1＋b)含能开得尽方的因数a2，不是最简二次根式；故选B.方法总结：最简二次根式必须同时满足下列两个条件：①被开方数中不含能开得尽方的因数或因式；②被开方数不含分母．判定一个二次根式是不是最简二次根式，就是看是否同时满足最简二次根式的两个条件，同时满足的就是最简二次根式，否则就不是．【类型二】二次根式的化简把下列各式化成最简二次根式．(1)500；(2)3a2b3；(3)2512；(4)23ab2.解析：(1)先将500分解质因数，再根据积的算术平方根的性质，把能够开尽方的因数100移到根号外；(2)根据积的算术平方根的性质，把能够开尽方的因式a2b2移到根号外；(3)把被开方数的分子、分母同时乘以3，把分母化为一个完全平方数，再把能开得尽方的部分移到根号外；(4)把被开方数的分子、分母同时乘以3a，把分母化为一个数的平方，再把分母移到根号外．解：(1)500＝100×5＝105；(2)3a2b3＝3b·a2b2＝|a|b3b；(3)2512＝25×312×3＝563；(4)23ab2＝2×3a3ab2·3a＝6a3ab.方法总结：把二次根式化成最简二次根式时，如果被开方数不含分母，则把被开方数尽量写成一个数的平方的形式，再利用积的算术平方根的性质化简；如果被开方数含有分母，可把分子、分母同乘以一个数，把分母化为一个数或式的平方的形式，再把分母开方后移到根号外，与此同时，分子中能开方的也要移到根号外．三、板书设计1．积的算术平方根的性质2．最简二次根式通过积的算术平方根与算术平方根的积的运算引入积的算术平方根的性质，让学生归纳总结出结论，并运用于化简．对于被开方数含有分母的二次根式化为最简二次根式是本节课的难点，引导学生根据分式的基本性质把分母化为一个数或式的平方，并让学生加强训练．。

二次根式第二课时教案教学目标：1. 理解二次根式的性质和运算法则。

2. 能够进行二次根式的化简、加减、乘除运算。

3. 能够应用二次根式解决实际问题。

教学重点：1. 二次根式的性质和运算法则。

2. 二次根式的化简、加减、乘除运算。

教学难点：1. 二次根式的化简和运算。

教学准备：1. 教学PPT。

2. 练习题。

教学过程：一、导入（5分钟）1. 复习一次根式的性质和运算法则。

2. 引入二次根式的概念，引导学生思考二次根式的性质和运算法则。

二、新课讲解（15分钟）1. 讲解二次根式的性质，如：二次根式中的被开方数相同，则两个二次根式相等；二次根式的乘除法法则，如：$\sqrt{a} \times \sqrt{b} = \sqrt{ab}$，$\sqrt{a} \div \sqrt{b} = \sqrt{\frac{a}{b}}$。

2. 讲解二次根式的化简方法，如：$\sqrt{a^2} = |a|$，$\sqrt{a^3} = a\sqrt{a}$。

三、案例分析（10分钟）1. 分析案例：化简二次根式$\sqrt{16}$。

解答：$\sqrt{16} = 4$。

2. 分析案例：计算二次根式的加减法$\sqrt{3} + \sqrt{5}$。

解答：无法合并，保持原样。

3. 分析案例：计算二次根式的乘除法$\sqrt{2} \times \sqrt{6}$。

解答：$\sqrt{2} \times \sqrt{6} = \sqrt{12} = 2\sqrt{3}$。

四、课堂练习（10分钟）1. 让学生独立完成练习题，巩固所学知识。

五、总结与反思（5分钟）1. 总结二次根式的性质和运算法则。

2. 反思自己在解题过程中的优点和不足。

教学延伸：1. 二次根式的混合运算。

2. 应用二次根式解决实际问题。

教学反思：本节课通过导入、新课讲解、案例分析、课堂练习和总结与反思等环节，让学生掌握了二次根式的性质和运算法则。

在教学过程中，要注意引导学生主动思考，培养学生的动手能力。

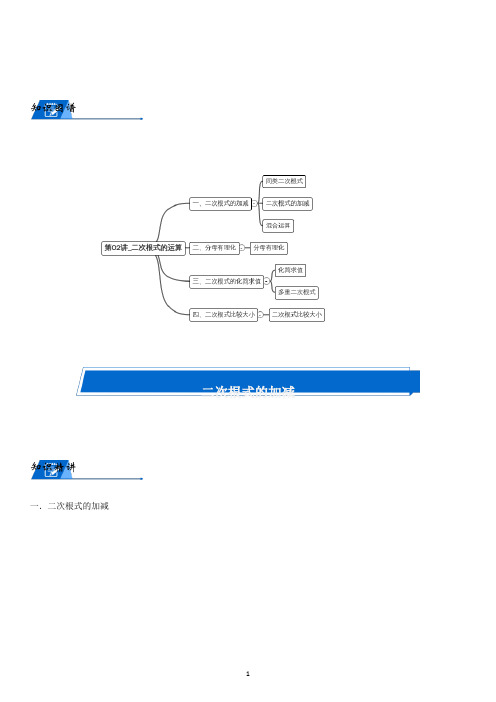
知识图谱二次根式的加减知识精讲一．二次根式的加减三点剖析一．考点：1．同类二次根式；2．二次根式的加减；3．混合运算．二．重难点：二次根式的混合运算，在计算的过程中注意结合学过的幂的运算和乘法公式简化计算过程．三．易错点：化成最简二次根式后被开方数仍不相同的二次根式不能加减合并，例如235+≠．同类二次根式例题1、 如果最简二次根式3b a b -和22b a -+是同类二次根式，那么a 、b 的值分别是（ ） A.0a =，2b = B.2a =，0b = C.1a =-，1b = D.1a =，2b =-同类二次根式二次根式化成最简二次根式后，如果被开方数相同，则称为同类二次根式（1）为同类二次根式（2）若最简二次根式 与可以合并，则二次根式的加减（1）先化成最简二次根式 （2）将同类二次根式合并，混合运算 先乘方，后乘除，最后加减，有括号的先计算括号里面的32x y 32x yz 2b a 2a b274x y 38xy3245a b 235a b例题3、 在下列各组根式中，是同类二次根式的是（ ）212 3ab 23a b 2121a -1a +随练1、 122223273 ） A.①和② B.②和③C.①和④D.③和④随练2、 下列二次根式：（112（222；（323；（4273 ） A.（1）和（4）B.（2）和（3）C.（1）和（2）D.（3）和（4）随练3、 若最简二次根式125a ++34b a +是同类二次根式，则____a =，____b =二次根式的加减例题1、 下列计算正确的是（ ）A.4333=1 235 1132=28 22（11148275278+（2）11(30.54 1.5)(0.244)22-（3212(1215)38（4）333y xx y x y xyx y随练1、下列四个算式正确的是（）336 B.2332= ()()4949-⨯--- D.43331-=随练2、计算：（1481233（2(18827÷混合运算例题1、下列计算正确的是（）3251233326=84 2=例题2、 计算：（1）()23122⎛⎫-- ⎪⎝⎭ （2）12-例题3、 计算：(231⎛+ ⎝=__________； ((((22221111+=__________；=__________．随练1、 计算：（1）（2）2++随练2、计算：（1(11213323-（2）(284821223-随练3、计算：（1）(33513716248a a a a⎛-⎝（2）11318503252⎛⎝（3）2353223302+（4）2210251025-分母有理化知识精讲分母有理化在二次根式的运算中，把分母中的根号去掉的过程称为分母有理化分母有理化形式（1）a a b ab bbbb==()()()()()22121a ba ba ba ba ba ba ba b ---===-++--（）()()()()()2211a ba ba b a b a ba b a ba b +++===---+-例：77214(1)==2222⨯⨯；()()12323321232323--===--++⨯-三点剖析一．考点：分母有理化．二．重难点：1．分母中只含有单独的一个二次根式时，分子分母同时乘以这个二次根式，利用2aa =从而消掉分母中的根号；2．当分母为两个二次根式相加减时，分子分母同时乘以这两个二次根式相减加，利用平方差公式从而消掉分母中的根号。

二次根式的加减法（第二课时）概述在数学中，二次根式是指以根号形式表示的含有平方根的表达式。

二次根式的加减法是对这样的表达式进行求和或求差的操作。

本文将介绍二次根式的加减法的基本概念和步骤，并通过一些例子来帮助读者理解和掌握这个重要的数学技巧。

二次根式的定义二次根式是形如√a或a√b的表达式，其中a和b是实数，且b大于0。

其中，a√b的形式称为含有系数的二次根式，√a的形式称为不含有系数的二次根式。

二次根式的加法二次根式的加法是指对两个二次根式进行求和的操作。

要执行二次根式的加法，需要满足以下两个条件：1.两个二次根式的根号下的数目和根号前的系数必须相同。

2.如果两个二次根式的根号前的系数不同，需要将它们化为相同的琍（即通分），再进行求和。

例子1我们以一个简单的例子来说明二次根式的加法：√3 + 2√3要求这两个根式的和，首先我们注意到根号下的数目都是3，根号前的系数分别是1和2。

由于这两个系数不同，我们需要将它们化为相同的分母。

这里我们可以将第一个根式的系数2改为2的平方，即2√3 = √12，然后再进行求和。

√3 + √12现在根号前的系数相同了，我们可以将根号下的数目相加。

√3 + √12 = 3√3所以，√3 + 2√3 = 3√3我们再来看一个复杂一些的例子：3√5 + 2√7 - √5对于这个表达式，我们首先注意到根号下的数目有两个5和7，根号前的系数分别是3、2和-1。

这里我们需要将这些根式化为相同的分母。

首先，将第一个根式和最后一个根式化为相同的表达式：3√5 - √5 = 2√5现在，我们重新整理一下表达式：2√5 + 2√7因为根号下的数目相同而且根号前的系数也相同，所以将它们相加即可：2√5 + 2√7 = 4√5 + 2√7所以，3√5 + 2√7 - √5 = 4√5 + 2√7二次根式的减法二次根式的减法是指对两个二次根式进行求差的操作。

要执行二次根式的减法，需要满足以下两个条件：1.两个二次根式的根号下的数目和根号前的系数必须相同。

二次根式的加减教案第二课时
教学目标：
- 理解二次根式的加减法则;
- 掌握二次根式的加减运算;
- 培养学生的运算能力和抽象思维能力。

教学准备：
- 课件;
- 二次根式的概念和加减法则;
- 例子。

教学过程:
Step 1:引入
- 同学们，前几天我们学习了二次根式的概念和运算，今天我们一起来探讨二次根式的加减运算。

Step 2:复习
- 请同学们复习一次根式的加减运算，老师会从中选取几个有代表性的问题请同学们回答。

Step 3:教学新内容
- 二次根式的加减法则：
- 先去括号，然后通分，最后按照乘法分配律进行运算。

- 举例说明：
(3x+2) + (4x-1) = 7x + 3
(3x-2) - (4x+1) = 7x - 3
Step 4:练习
- 请同学们针对老师给出的二次根式问题进行运算，并且指出他们遇到的问题，老师进行解答。

Step 5:总结
- 同学们，今天我们学习了二次根式的加减运算，我们通过例子深刻体会到了二次根式的加减法则，希望你们能够熟练掌握，并且能够应用到实际问题中。

教学反思：
- 二次根式的加减运算比较抽象，需要同学们通过实际操作和举例才能够理解，老师可以通过课件和例子来帮助同学们加深对二次根式的理解。

- 在教学过程中，需要注意引导学生进行操作和思考，并且及时给予指导和帮助，保证同学们都能够理解和掌握二次根式的加减运算。