正切和余切

三角函数的倒数与余切与余割与正割与余弦与正弦公式三角函数是数学中常见的一类函数，包括正弦、余弦、正切、余切、正割、余割六种。

在三角函数中，倒数与余切与余割与正割与余弦与正弦之间存在一些特定的公式和关系。

本文将探讨这些公式和关系，并介绍它们的应用。

一、倒数与余切公式倒数是指一个数的倒数，记作x的倒数为1/x。

在三角函数中，正切的倒数称为余切，表示为cot(x)。

余切的定义为余切(x) = 1/tan(x)。

余切(x)有以下公式：cot(x) = cos(x)/sin(x)cot(x) = 1/tan(x)倒数与余切公式的应用非常广泛。

它们在解三角方程、计算三角函数值和求解实际问题中经常被使用。

二、余割与正割公式余割和正割是三角函数中与正弦和余弦有关的函数。

余割的定义为csc(x) = 1/sin(x)。

余割(x)有以下公式：csc(x) = 1/sin(x)csc(x) = 1/cos(x)/tan(x) = cos(x)/sin(x)正割的定义为sec(x) = 1/cos(x)。

正割(x)有以下公式：sec(x) = 1/cos(x)sec(x) = 1/sin(x)/cot(x) = 1/cos(x)/sin(x)余割与正割公式的应用也非常广泛。

它们在解三角方程、计算三角函数值和求解实际问题中经常被使用。

三、余弦与正弦公式余弦和正弦是三角函数中最为常见的两种函数。

余弦与正弦有以下公式：cos(x) = 1/sin(x)/tan(x)cos(x) = sqrt(1 - sin^2(x))（平方根）cos^2(x) + sin^2(x) = 1正弦与余弦公式在解三角方程、计算三角函数值和求解实际问题中都有重要的应用。

综上所述，三角函数的倒数与余切与余割与正割与余弦与正弦公式在数学和实际应用中起着重要的作用。

这些公式可以帮助我们解决各种三角函数相关的问题，提高计算的准确性和效率。

因此，在学习和应用三角函数时，我们应该充分理解和掌握这些公式的意义和用法。

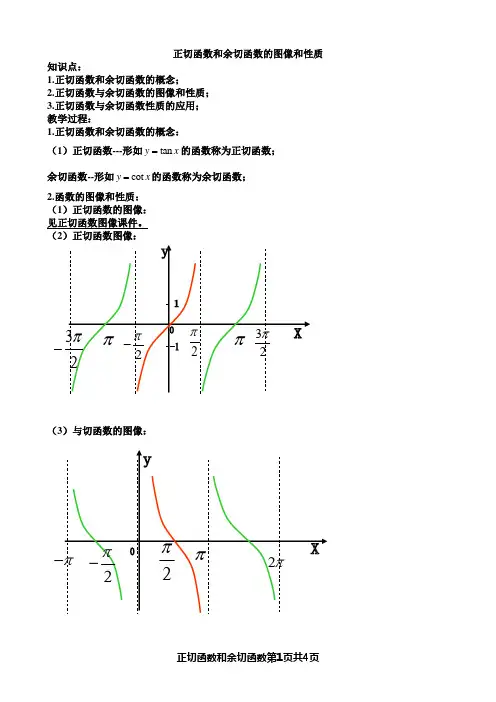
正切函数和余切函数的图像和性质知识点：1.正切函数和余切函数的概念；2.正切函数与余切函数的图像和性质；3.正切函数与余切函数性质的应用；教学过程：1.正切函数和余切函数的概念：（1）正切函数---形如tan=的函数称为正切函数；y x余切函数--形如coty x=的函数称为余切函数；2.函数的图像和性质：（1）正切函数的图像：见正切函数图像课件。

（2）正切函数图像：-（3）与切函数的图像：例1.求下列函数的周期： （1）tan(3)3y x π=-+；（2）221tgx y tg x=+；（3）cot tan y x x =-；（4）22tan21tan2x y x =-；（5）sin 1tan tan2x y x x ⎛⎫=+ ⎪⎝⎭例2.求下列函数的单调区间： （1）tan(2)24y x π=++； （2）tan()123x y π=-+-；（3）12log cot 3y x ⎛=-⎝⎭例3.求下列函数的定义域：（1）tan 4y x π⎛⎫=-⎪⎝⎭；（2）y =（3）y =例4.（1）求函数21)tan tan ]y x x =-+的定义域；（2）解不等式：23tan (2)(3tan(2)044x x ππ+--+-≤例5.已知2tan tan y x a x =-，当1[0,],[0,]34x a π∈∈时，函数max y =，求实数a 的值；例6.已知函数tan ,(0,)2y x x π=∈，若1212,(0,),2x x x x π∈≠。

求证：1212()()()22f x f x x x f ++>。

函数名正弦余弦正切余切正割余割这些函数都是三角函数的一部分，它们在数学和物理中都有广泛的应用。

以下是对这些函数的基本介绍：1.正弦函数（Sine Function）和余弦函数（Cosine Function）：正弦函数和余弦函数都与三角形的边长有关。

在直角三角形中，正弦函数是三角形的对边（opposite）与斜边（hypotenuse）的比值，记为sin(x)；余弦函数是三角形的邻边（adjacent）与斜边的比值，记为cos(x)。

正弦和余弦函数的图像都是周期性的，这意味着它们在一定间隔内重复。

2.正切函数（Tangent Function）和余切函数（Cotangent Function）：正切函数和余切函数是正弦函数和余弦函数的比值。

正切函数是正弦函数除以余弦函数，记为tan(x)；余切函数是余弦函数除以正弦函数，记为cot(x)。

正切函数的图像也是周期性的，但余切函数的图像并非周期性。

3.正割函数（Secant Function）和余割函数（Cosecant Function）：正割函数和余割函数分别是正弦函数和余弦函数的倒数。

正割函数是sec(x) = 1/cos(x)，余割函数是csc(x) = 1/sin(x)。

它们的图形也是周期性的。

这些函数在三角学中有着重要的应用。

例如，它们可以用来描述振动、波动、声音传播等物理现象。

在计算机图形学中，这些函数也常被用来生成旋转、缩放、平移等变换。

此外，这些函数在解决一些数学问题时也非常有用，比如求解极值、最优解、零点等。

除了基本的三角函数，还有许多派生出来的三角函数，如反正弦函数（Inverse Sine Function）、反余弦函数（Inverse Cosine Function）、反正切函数（Inverse Tangent Function）等。

这些函数的定义域是有限的，值域是整个实数集。

它们通常被用于求解一些方程的根，比如求解三角形的角度等。

三角函数的诱导公式知识点三角函数的诱导公式是数学中关于三角函数之间的一组等式，通过这组等式可以在不依赖计算器或表格的情况下直接计算出一些角度的三角函数值，从而简化计算。

诱导公式的基本思想是通过将一个角度的三角函数转化为另一个角度的三角函数来求解。

一、正弦和余弦的诱导公式：根据正弦函数和余弦函数的定义，对于任意角度θ，有：sin θ = y/rcos θ = x/r其中，x，y，r代表直角三角形中的边长。

利用勾股定理可以得到x²+y²=r²。

现在考虑角度θ+90°，即sin(θ+90°)和cos(θ+90°)的值。

根据正弦函数和余弦函数的定义，有：sin(θ+90°) = y’/rcos(θ+90°) = x’/r其中，x’，y’，r由右边角相等可知。

然后考虑直角三角形中的边长关系：y’=xx’=-y(由右边角相等，即90°+(-θ))代入sin(θ+90°)和cos(θ+90°)，得到：sin(θ+90°) = x/r，即sin(θ+90°) = cosθcos(θ+90°) = -y/r，即cos(θ+90°) = -si nθ得到正弦的诱导公式：sin(θ+90°) = cosθ；得到余弦的诱导公式：cos(θ+90°) = -sinθ。

利用这两个诱导公式，我们可以在计算中互相转化正弦和余弦的值。

二、正切和余切的诱导公式：正切和余切的定义是：tan θ = sin θ / cos θcot θ = cos θ / sin θ。

根据正弦和余弦的诱导公式，我们可以得到：sin(θ+90°) = cosθcos(θ+90°) = -sinθ。

将这两个式子带入正切和余切的定义，有：tan(θ+90°) = sin(θ+90°) / cos(θ+90°) = cosθ / (-sinθ) = -cotθcot(θ+90°) = cos(θ+90°) / sin(θ+90°) = (-sinθ) /cosθ = -tanθ。

三角函数的特殊值和周期性三角函数是数学中的一个重要分支，可以用于描述周期性和振荡现象，如波浪、振动、电信号等。

在学习三角函数时，需要掌握它们的特殊值和周期性，这对于解题和理解三角函数的性质非常关键。

一、正弦函数和余弦函数的特殊值正弦函数和余弦函数是最基本的三角函数，在计算中常常需要用到它们的特殊值。

以下是正弦函数和余弦函数在0°、30°、45°、60°、90°这几个角度下的值：正弦函数的特殊值：sin(0°)=0, sin(30°)=1/2, sin(45°)=√2/2,sin(60°)=√3/2, sin(90°)=1余弦函数的特殊值：cos(0°)=1, cos(30°)=√3/2, cos(45°)=√2/2,cos(60°)=1/2, cos(90°)=0需要注意的是，在计算中所使用的函数值是弧度制下的值。

二、正切函数和余切函数的特殊值正切函数和余切函数在三角函数中也是非常重要的一类函数，它们和正弦函数、余弦函数的关系也非常密切。

以下是正切函数和余切函数在0°、30°、45°、60°、90°这几个角度下的值：正切函数的特殊值：tan(0°)=0, tan(30°)=1/√3, tan(45°)=1, tan(60°)=√3, tan(90°)不存在余切函数的特殊值：cot(0°)不存在, cot(30°)=√3, cot(45°)=1,cot(60°)=1/√3, cot(90°)=0三、三角函数的周期性三角函数的周期性是指函数呈现出一定的规律性，即在一定的区间内，函数的值不断变化，然而这种变化呈现出一定的规律性，与前一个周期内的变化情况相似。

数学教案－正切和余切_九年级数学教案_模板锐角的三角比------正切和余切一、教学目标：1、理解锐角的正切、余切概念，能正确使用锐角的正切、余切的符号语言。

2、通过探究活动，培养学生观察、分析问题，归纳、总结知识的能力；通过题目的变式，培养用转化思想解决数学问题的能力；通过不同题型的训练，提高学生的通试能力；通过探索题的教学，培养学生的创新意识。

3、通过不同题型的训练，培养学生的数学学习素养，通过学习形式的变换，孕育学生的品质。

4、培养学生间良好的互动协作精神和对知识强烈的求知欲。

二、教学设计的指导思想：贯彻“教为主导、学为主体、练为主线”的原则，引导学生自始至终地参与学习的全过程，让学生在探索过程中学得愉快、扎实、灵活，学会学习，发展能力。

三、重、难点及教学策略：重点：锐角的正切、余切概念，探究能力的培养难点：理解一个锐角确定的直角三角形的两边的比是一个确定的值。

策略：突出重点、突破难点。

四、教学准备：U盘，电脑，一副三角板，一块三角形模型，网格纸五、教学环节的流程简图：创设问题情境——→ 问题的研究——→ 讲授新课——→ 归纳小结及布置作业六、教学过程（）：一）创设问题情境：1、引领练习：①在Rt△ABC中，∠C=90°，当∠A=45°时，随着三角形的边长的放大或缩小时，上面的比值是否发生变化？②在Rt△ABC中，∠C=90°，当∠A=30°时，随着三角形的边长的放大或缩小时，上面的比值是否发生变化？2、提出问题：在Rt△ABC中，∠C=90°，一般情况下，当∠A的大小确定，三角形的边长的放大或缩小时，上面的比值是否发生变化？二）问题的研究：1、几何画板动画演示：2、运用定理证明：得出结论：在Rt△ABC中，∠C=90°，一般情况下，当∠A的大小确定，三角形的边长的放大或缩小时，上面的比值不变。

三）讲授新课：课题：29.1 正切和余切1、基本概念：①在Rt△ABC中，∠C=90°，正切：tgA= =（tangent）（tanA）（tg∠BAC）余切：ctgA= =（cotA）②tgA=③若∠A+∠B=90°，则tgA=ctgB ，ctgA=tgB2、例题讲解：例1：在Ｒｔ△ＡＢＣ中，∠Ｃ＝９０°，ＡＣ＝１２，ＢＣ＝７，①求ｔｇＡ的值．②求ｔｇＢ的值．③过Ｃ点作ＣＤ⊥ＡＢ于Ｄ，求ｔｇ∠ＤＣＡ的值．3、巩固练习：①选择题：1.在Rt△ABC中, ∠C＝90°,若各边的长都扩大3倍,则∠B的正切值( )A.扩大3倍B.缩小为原来的C.没有变化D.扩大9倍2.在Rt△ABC中, ∠C＝90°, ∠A和∠B的对边是a,b,则与的值相等的是( )A.tgAB.tgBC.ctgAD.ctgB②解答题：如图，△ＡＢＣ是直角三角形，∠Ｃ＝９０°，Ｄ、Ｅ在ＢＣ上，ＡＣ＝４，ＢＤ＝５，ＤＥ＝２，ＥＣ＝３，∠ＡＢＣ＝α，∠ＡＤＣ＝β，∠ＡＥＣ＝γ，求：①ｔｇα。

余切,正割,余割函数求导在微积分学中，我们经常会遇到三角函数的求导问题。

三角函数包括：正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数。

其中，正割函数和余割函数的求导相对来说比较容易，但是，余切函数的求导可能会让人感到困惑。

在本文中，我们将详细介绍余切、正割和余割函数的求导方法。

一、余切函数求导先来看一下余切函数的定义：$\cot{a}=\frac{1}{\tan{a}}=\frac{\cos{a}}{\sin{a}}$。

我们可以用导数的定义来求余切函数的导数：$$\frac{d}{dx}\cot{x} = \lim_{h \to 0} \frac{\cot{(x+h)} -\cot{x}}{h}$$将 $\cot{(x+h)}$ 和 $\cot{x}$ 的值带入，并将分式进行化简得：$$\frac{d}{dx}\cot{x} = \lim_{h \to 0}\frac{\frac{\cos{(x+h)}}{\sin{(x+h)}} -\frac{\cos{x}}{\sin{x}}}{h} \\= \lim_{h \to 0} \frac{\cos{(x+h)}\sin{x} -\cos{x}\sin{(x+h)}}{h\sin{(x+h)}\sin{x}} \\= \lim_{h \to 0} \frac{\cos{(x+h)}\sin{x} -\cos{x}\sin{(x+h)}}{h\sin{x}\cos{h} + h\cos{x}\sin{h}} \\= \lim_{h \to 0} \frac{\cos{(x+h)}\sin{x} -\cos{x}\sin{(x+h)}}{h(\sin{x}\cos{h} + \cos{x}\sin{h})} \\ = \lim_{h \to 0} \frac{\cos{x}\sin{h} -\sin{x}\cos{h}}{h(\sin{x}\cos{h} + \cos{x}\sin{h})} \\= -\frac{1}{\sin^2{x}}$$因此，余切函数的导数为 $-\frac{1}{\sin^2{x}}$。

常用的九个三角函数值表
在数学中，三角函数是描述角的函数，共有六个基础三角函数：正弦、余弦、正切、余切、正割和余割。

这些函数在数学和科学领域中具有广泛的应用。

在本文中，我们将列出常用的九个三角函数值表，包括正弦、余弦、正切、余切、正割、余割、余弦、余切、余割函数的计算结果。

常用的九个三角函数值表
正弦函数值表
角度（°）正弦值
00
301/2
45√2/2
60√3/2
901
余弦函数值表
角度（°）余弦值
01
30√3/2
45√2/2
601/2
900
正切函数值表
角度（°）正切值
00
30√3/3
451
60√3
90无穷大
余切函数值表
角度（°）余切值
0无穷大
30√3
451
60√3/3
900
正割函数值表
角度（°）正割值
0无穷大
302/√3
45√2
602
901
余割函数值表
角度（°）余割值
01
30√3/3
45√2
602/√3
90无穷大
总结
在数学中，三角函数是非常重要的概念，它们在各种科学和工程领域中均有广泛的应用。

通过熟练掌握常用的九个三角
函数的数值表，我们可以更好地理解和解决与角度和三角函数相关的问题。

希望这份三角函数值表可以帮助您更好地理解这一内容。

以上就是我整理的常用的九个三角函数值表，希望对您有所帮助！。

三角函数余切,正割,余割和差角,半角,二倍角等公式三角函数，也叫三角形函数，是一类函数，可以表示和描述二维空间中三角形的属性、性质等，是非常重要的数学概念。

本文将主要介绍其中一些关于三角形的函数，如余切、正割、余割和差角、半角、二倍角等。

一、余切对于任一定模式三角形，我们可以把它分成三角形的各边和角，且每个角都有自己的度数，记作α，β，γ。

现在，我们把α的正切函数的反函数，就是α的余切函数，它的标记为tg(α)的倒函数，记作cotg(α)，它可以用来表示三角形角α的余切。

公式表示为：cotg=tan (90°-α)二、正割对于任一定模式三角形，我们可以把它分成三角形的各边和角，即α、β、γ，α的正割函数的反函数就是α的正割，它的标记为ctg(α)，它的定义为：把α的正弦函数的倒函数，即sin(α)的倒函数定义为α的正割函数。

公式表示为：ctg=cos (90°-α)三、余割余割与正割的定义类似，余割的定义为α的余弦函数的倒函数，它的标记为cosec(α)，它的定义为：把α的余弦函数的倒函数，即cos(α)的倒函数定义为α的余割函数。

公式表示为：cosec =sin (90°-α)四、差角差角就是把两个角之间的夹角表达出来，该夹角就是所谓的差角。

差角可由以下公式表示：差角=α+β-γ其中，α、β、γ分别是三角形的三个角。

五、半角半角指的是三角形中某一角的一半，即α的一半。

其定义为：α的一半，可由以下公式表示：半角/2=α/2六、二倍角二倍角指的是三角形中某一角的两倍，即α的两倍。

该角度可表示为：二倍角 2α=2α以上就是关于三角函数的余切、正割、余割和差角、半角、二倍角等公式的介绍。

三角函数有着非常重要的概念和应用，熟悉三角函数，不但能帮助我们掌握一般函数的概念，而且可以帮助我们解决数学问题，提高学习效率，拓宽我们的知识面。

《正切和余切》数学教案一、教学目标：1. 让学生理解正切和余切的定义，掌握它们的性质和运算方法。

2. 培养学生运用正切和余切解决实际问题的能力。

3. 提高学生对三角函数的学习兴趣，培养学生的逻辑思维能力。

二、教学内容：1. 正切和余切的定义及性质2. 正切和余切的运算方法3. 正切和余切在实际问题中的应用三、教学重点与难点：1. 重点：正切和余切的定义，性质，运算方法。

2. 难点：正切和余切的运算方法在实际问题中的应用。

四、教学方法：1. 采用讲授法，讲解正切和余切的定义、性质和运算方法。

2. 采用案例分析法，分析正切和余切在实际问题中的应用。

3. 采用小组讨论法，引导学生探讨正切和余切的关系。

五、教学过程：1. 导入：回顾正弦和余弦的概念，引导学生思考正切和余切的定义。

2. 讲解：讲解正切和余切的定义、性质和运算方法，结合实际例子进行分析。

3. 练习：布置练习题，让学生巩固正切和余切的知识。

4. 案例分析：分析正切和余切在实际问题中的应用，如测量角度、计算物体的高度等。

5. 小组讨论：引导学生探讨正切和余切的关系，总结它们的异同点。

6. 总结：对本节课的内容进行总结，强调正切和余切的重要性。

7. 作业布置：布置课后作业，巩固所学知识。

六、教学评估：1. 课后作业：布置有关正切和余切的习题，评估学生对知识的掌握程度。

2. 课堂练习：在课堂上进行正切和余切的练习，观察学生的解题过程，了解他们的学习情况。

3. 小组讨论：评估学生在小组讨论中的表现，了解他们对于正切和余切的理解和应用能力。

七、教学资源：1. 教材：正切和余切的相关章节。

2. 投影片：正切和余切的性质和运算方法的投影片。

3. 计算机软件：用于绘制函数图像，帮助学生更好地理解正切和余切。

八、教学进度安排：1. 第一课时：介绍正切和余切的定义及性质。

2. 第二课时：讲解正切和余切的运算方法。

3. 第三课时：分析正切和余切在实际问题中的应用。

余割函数和正切函数的关系余割函数和正切函数是几何学中常见的两类函数，它们的定义域和值域都是实数集，很容易发现它们之间的关系。

余割函数，也被称为反正切函数，可以定义为：对每个实数x，余割函数的值y即为arctan(x)的值，其中arctan(x)为实数x的正切函数值。

因此，余割函数用于将实数x的正切函数值arctan(x)转换成实数y。

正切函数可以定义为：对于任意一个实数x，tan(x)即为实数x 的正切函数值。

由于实数x的正切函数值必须是一个实数，故tan(x)一定是要么是一个实数，要么是一个有理数。

由于余割函数和正切函数都是实数集上的函数，它们之间存在一定的关系。

首先，它们都是关于实数集上的单射函数，即它们都是一对一映射函数，其中余割函数是从实数的正切函数值到实数的一对一映射，而正切函数则是从实数到实数的正切函数值的一对一映射。

此外，余割函数和正切函数之间还有一个很重要的关系，即余割函数和正切函数是反函数。

这意味着实数x的正切函数值arctan(x)可以被映射到实数y，即y=arctan(x)，而实数y的正切函数值可以通过arctan(y)的形式来求出，即x=arctan(y)。

由此可以看出，余割函数和正切函数是互为反函数的。

除此之外，余割函数和正切函数之间还存在另一个关系，即它们的图像是完全一致的。

也就是说，余割函数的图像可以通过x轴翻转得到正切函数的图像，反之亦然。

以上讲述了余割函数和正切函数之间的一些关系，它们之间显然是相关联的，因此，学习它们之间的关系对于我们正确理解和使用这两类函数都有很大的帮助。

当我们需要求某个实数的余割函数值时，可以先求出该实数的正切函数值，然后将其代入到余割函数中求出它的值；反之，如果想要求实数的正切函数值，可以先求出实数的余割函数值，再将其代入到正切函数中求出它的正切函数值。

总之，余割函数和正切函数之间非常渊源，它们之间存在多项重要的关系，学习和理解这些关系将有助于我们更好地理解和应用余割函数和正切函数。

三角函数正弦,余弦,正切,余切是什么意思牛顿45。

正切函数为什么叫正切？正弦、余弦、正切、余切三角函数：…常见的三角函数有正弦函数、余弦函数和正切函数。

…函、数、函数，正、弦、正弦，余、弦、余弦，切：见《牛顿44》…正切：在Rt△ABC（直角三角形）中，∠C=90°，AB是∠C的对边c，BC是∠A的对边a，AC是∠B的对边b，正切函数就是tanB=b/a，即tanB=AC/BC。

在物理学中，三角函数也是常用的工具。

在Rt△ABC中，如果锐角A确定，那么角A的对边与邻边的比值随之确定，这个比叫做角A的正切，记作tanA。

即：tanA=∠A的对边/∠A的邻边。

tan 为什么称为正切？正切的解释是什么？——网友提问…tan：tangent的简写……tangent（英文）：n.切线; 正切……解、释、解释：见《欧几里得56》…（…《欧几里得》：小说名…）匿名用户：首先，我们有一个角θ…θ：希腊字母西塔Theta（大写Θ，小写θ），在希腊语中，是第八个希腊字母。

国际音标：/'θi:tə/小写的θ是：数学上常代表平面的角…以角的端点为圆心，作一个单位圆（也就是半径为1的圆）然后这个圆肯定与我们的角有两个交点随便选一个交点，作一条圆的切线然后这条切线被θ角的两条射线所截，形成一条线段这条线段的长度就是tanθ，即θ的正切值…值：见《欧几里得74》…同理，我们也可以接着从这个点，作一条圆的弦这个弦被θ角的两条射线所截，形成一条线段这条线段的长度就是sinθ，即θ的正弦值至于余弦、余切。

顾名思义，正如@南中国海的一条鱼所说。

θ余角的正弦，就是θ的余弦θ余角的正切，就是θ的余切编辑于2014-12-18（39人赞同了该回答）“还在很早的时候，由于垦（kěn）殖和畜（xù）牧的需要，人们就开始作长途迁移；后来，贸易的发展和求知的欲望，又推动他们去长途旅行。

在当时，这种迁移和旅行是一种冒险的行动。

正切余切正割余割在数学的三角函数世界里，正切、余切、正割、余割是四个重要的概念。

它们在解决几何问题、物理问题以及工程应用中都发挥着关键的作用。

咱们先来聊聊正切。

正切用符号“tan”表示，它是一个角的对边与邻边的比值。

简单来说，如果我们有一个直角三角形，一个锐角所对应的对边长度为 a，邻边长度为 b，那么这个角的正切值就是 a/b。

比如说，一个角的对边是 3，邻边是 4，那这个角的正切值就是 3/4。

正切函数的图像可是很有特点的。

它的定义域是整个实数集，但要除去一些特殊的点，比如π/2 ＋kπ（k 是整数），因为在这些点上，正切函数是没有定义的。

正切函数的图像在定义域内是周期性的，周期是π。

而且，它的图像在不同的区间内呈现出不同的增减性。

接着说说余切。

余切用“cot”表示，它是邻边与对边的比值。

还是用刚才那个直角三角形举例，如果对边是 a，邻边是 b，那这个角的余切值就是 b/a。

余切函数的定义域也是除去一些特殊点的实数集，它的周期同样是π。

正切和余切之间有着密切的关系。

它们互为倒数，也就是说tanα × cotα ＝ 1。

这一关系在解决很多数学问题时都能派上用场。

再来讲讲正割。

正割用“sec”表示，它是斜边与邻边的比值。

对于那个直角三角形，斜边长度是 c，邻边长度是 b，那么这个角的正割值就是 c/b。

正割函数的定义域也是除去一些特殊点的实数集。

余割呢，用“csc”表示，是斜边与对边的比值。

在同一个直角三角形中，如果斜边是 c，对边是 a，那么这个角的余割值就是 c/a。

正割和余割之间也存在类似正切和余切的关系，那就是secα × cscα＝ 1。

在实际应用中，正切、余切、正割、余割都非常有用。

比如在物理学中，研究波动现象、交流电等问题时，经常会用到这些三角函数。

在工程领域，计算建筑物的倾斜度、桥梁的受力分析等，也离不开它们。

咱们通过一个具体的例子来感受一下。

假设要计算一个斜坡的坡度，我们就可以用正切来表示。

三角函数公式大全本文主要介绍三角函数公式的大全，包括正弦、余弦、正切、余切、正割、余割、弧度制、角度制等，共计52个公式。

三角函数是初等数学中重要的一部分，以它为基础可以推导出很多数学公式，也是物理、化学等自然科学中常用的数学工具。

1、正弦(sin)与余弦(cos)的关系公式sin θ = cos(90° - θ)cos θ = sin(90° - θ)2、正弦(sin)与余切(ctg)的关系公式sin θ = 1 / ctg θctg θ = 1 / sin θ3、正弦(sin)与正割(sec)的关系公式sin θ = 1 / sec(90° - θ)sec θ = 1 / sin(90° - θ)4、余弦(cos)与正切(tan)的关系公式cos θ = 1 / tan(90° - θ)tan θ = 1 / cos(90° - θ)5、余弦(cos)与余切(cot)的关系公式cos θ = 1 / cot(90° - θ)cot θ = 1 / cos(90° - θ)6、余弦(cos)与余割(cosec)的关系公式c os θ = 1 / cosec(90° - θ)cosec θ = 1 / cos(90° - θ)7、正切(tan)与余切(cot)的关系公式tan θ = 1 / cot θcot θ = 1 / tan θ8、正切(tan)与正割(sec)的关系公式tan θ = 1 / sec(90° - θ)sec θ = 1 / cot(90° - θ)9、正切(tan)与余割(cosec)的关系公式tan θ = 1 / cosec(90° - θ)cosec θ = 1 / cot(90° - θ)10、余切(cot)与正割(sec)的关系公式cot θ = 1 / sec θsec θ = 1 / cot θ11、余切(cot)与余割(cosec)的关系公式cot θ = 1 / cosec(90° - θ)cosec θ = 1 / tan(90° - θ)12、正割(sec)与余割(cosec)的关系公式sec θ = 1 / cosec(90° - θ)cosec θ = 1 / sec(90° - θ)13、正弦(sin)的倒数公式sin(-θ) = -sin θsin(θ ± 360°) = sin θ14、余弦(cos)的倒数公式cos(-θ) = cos θcos(θ ± 360°) = cos θ15、正切(tan)的倒数公式tan(-θ) = -tan θtan(θ ± 180°) = tan θ16、余切(cot)的倒数公式cot(-θ) = -cot θcot(θ ± 180°) = cot θ17、正割(sec)的倒数公式sec(-θ) = sec θsec(θ ± 360°) = sec θ18、余割(cosec)的倒数公式cosec(-θ) = -cosec θcosec(θ ± 360°) = cosec θ19、正弦(sin)的平方公式sin² θ + cos² θ = 11 - sin² θ = cos² θsin² θ = 1 - cos² θ20、余弦(cos)的平方公式sin² θ + cos² θ = 11 - cos² θ = sin² θcos² θ = 1 - sin² θ21、正切(tan)的平方公式tan² θ + 1 = sec² θ1 + cot² θ = cosec² θtan² θ = sec² θ - 122、余切(cot)的平方公式cot² θ + 1 = cosec² θ1 + tan² θ = sec² θcot² θ = cosec² θ - 123、正弦(sin)的角和公式sin(A + B) = sin A cos B + cos A sin Bsin(A - B) = sin A cos B - cos A sin B 24、余弦(cos)的角和公式cos(A + B) = cos A cos B - sin A sin B cos(A - B) = cos A cos B + sin A sin B 25、正弦(sin)的二倍角公式sin 2A = 2 sin A cos A26、余弦(cos)的二倍角公式cos 2A = cos² A - sin² A27、正切(tan)的二倍角公式tan 2A = 2 tan A / (1 - tan² A)28、余切(cot)的二倍角公式cot 2A = (cot² A - 1) / 2 cot A29、正割(sec)的二倍角公式sec 2A = (sec² A + 1) / (2 sec A)30、余割(cosec)的二倍角公式cosec 2A = (cosec² A + 1) / (2 cosec A) 31、正弦(sin)的三倍角公式sin 3A = 3 sin A - 4 sin³ A32、余弦(cos)的三倍角公式cos 3A = 4 cos³ A - 3 cos A33、正切(tan)的三倍角公式tan 3A = (3 tan A - tan³ A) / (1 - 3 tan² A) 34、余切(cot)的三倍角公式cot 3A = (3 cot A - cot³ A) / (3 cot² A - 1) 35、正弦(sin)的四倍角公式sin 4A = 4 sin A cos A (2 cos² A - 1) 36、余弦(cos)的四倍角公式cos 4A = cos² 2A - sin² 2A37、正切(tan)的四倍角公式tan 4A = (4 tan A - 4 tan³ A) / (1 - 6 tan² A + tan⁴ A) 38、余切(cot)的四倍角公式cot 4A = (cot² 2A - 1) / 2 cot 2A39、正弦(sin)的半角公式sin (A/2) = ±√[(1 - cos A) / 2]40、余弦(cos)的半角公式cos (A/2) = ±√[(1 + cos A) / 2]41、正切(tan)的半角公式tan (A/2) = ±√[(1 - cos A) / (1 + cos A)]42、余切(cot)的半角公式cot (A/2) = ±√[(1 + cos A) / (1 - cos A)]43、正割(sec)的半角公式sec (A/2) = ±√[(1 + cos A) / (1 - cos A)]44、余割(cosec)的半角公式cosec (A/2) = ±√[(1 - cos A) / (1 + cos A)]45、正弦(sin)的万能公式a sin x +b cos x = √(a² + b²) sin(x + atan(b/a))46、余弦(cos)的万能公式a cos x -b sin x = √(a² + b²) cos(x + atan(b/a))47、正切(tan)的万能公式a tan x -b cot x = atan[(a sin x - b cos x)/(a cos x + b sin x)]48、余切(cot)的万能公式a cot x -b tan x = atan[(b sin x - a cos x)/(a sin x + b cos x)]49、正割(sec)的万能公式a sec x +b cosec x = 2 √(a² + b²) / [sin(2x + atan(b/a)) + sin(2x - atan(b/a))]50、余割(cosec)的万能公式a cosec x +b sec x = 2 √(a² + b²) / [sin(2x + atan(b/a)) - sin(2x - atan(b/a))]51、弧度制与角度制的转换公式弧度制 = 角度制× π / 180角度制 = 弧度制× 180 / π52、三角函数的图像正弦(sin)的图像：余弦(cos)的图像：正切(tan)的图像：余切(cot)的图像：正割(sec)的图像：余割(cosec)的图像：以上是三角函数公式的大全，通过掌握这些公式可以更深入地了解三角函数的性质和应用，有助于提高数学水平。

正切函数和余切函数的图像和性质知识点：1.正切函数和余切函数的概念；2.正切函数与余切函数的图像和性质；3.正切函数与余切函数性质的应用；教学过程：1.正切函数和余切函数的概念：（1）正切函数---形如tan=的函数称为正切函数；y x余切函数--形如cot=的函数称为余切函数；y x2.函数的图像和性质：（1）正切函数的图像：见正切函数图像课件。

（2）正切函数图像：（3）与切函数的图像：（1）tan(3)3y x π=-+； （2）221tgx y tg x =+； （3）cot tan y x x =-；（4）22tan21tan 2xy x =-； （5）sin 1tan tan 2x y x x ⎛⎫=+ ⎪⎝⎭ 例2.求下列函数的单调区间：（1）tan(2)24y x π=++； （2）tan()123x y π=-+-； （3）12log cot 3y x ⎛=- ⎝⎭例3.求下列函数的定义域：（1）tan 4y x π⎛⎫=- ⎪⎝⎭； （2）y =（3）y=例4.（1）求函数21)tan tan ]y xx =-的定义域；（2）解不等式：23tan (2)(3tan(2)044x x ππ+-+≤ 例5.已知2tan tan y x a x =-，当1[0,],[0,]34x a π∈∈时，函数max y =，求实数a 的值； 例6.已知函数tan ,(0,)2y x x π=∈，若1212,(0,),2x x x x π∈≠。

求证：1212()()()22f x f x x x f ++>。