人教版初三数学下册余弦与余切
- 格式:doc
- 大小:110.50 KB
- 文档页数:2

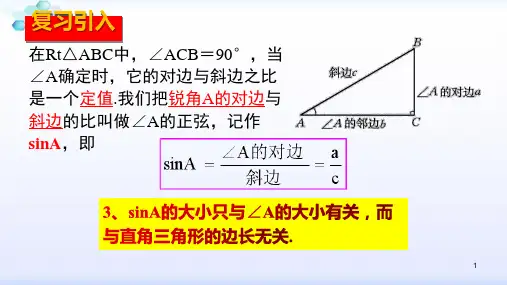






三角函数第二课时锐角三角函数之余弦和正弦教学目标:知识与技能:1、了解锐角三角函数的概念,能够正确应用sinA、cosA、tanA表示直角三角形中两边的比.2、逐步培养学生观察、比较、分析、概括的思维能力.过程与方法:通过锐角三角函数的学习,进一步认识函数,体会函数的变化与对应的思想,逐步培养学生会观察、比较、分析、概括等逻辑思维能力.情感态度与价值观:引导学生探索、发现,以培养学生独立思考、勇于创新的精神和良好的学习习惯.重难点:1.理解余弦、正切的概念.2.难点:熟练运用锐角三角函数的概念进行有关计算.教学过程:一.复习正弦的定义:在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦。
记作sinaA,即sinA=∠A的对边斜边二(学生思考,作答,说明为什么。
)探究二(小组讨论,作答,三角形的相似性质)(请写出证明过程,黑板上演示)三.总结展示新课:余弦的定义在RT△ABC中,在Rt△ABC中,∠C=90°,我们把锐角A的邻边与斜边的比叫做∠A的余弦。
记作cosA,即cosA=∠A的邻边斜边正切的定义:在RT△ABC中,在Rt△ABC中,∠C=90°,我们把锐角A的对边与邻边的比叫做∠A的正切。
记作tanA,即tanA=∠A的对边∠A的邻边四.新知巩固例一.在RT△ABC中,在Rt△ABC中,∠C=90°,BC=6,sinA=3/5,求cosA.tanA的值练习。
在RT△ABC中,在Rt△ABC中,∠C=90,cosA=15/17,求sinA.tanA的值例二.。
6
B ∠A的邻边b
∠A的对边a 斜边c
C
B
A 【学习课题】25.2.1 锐角三角函数(二) 【学习课型】新授课 【学习课时】1课时 【学习目标】
(1)经历探索直角三角形中边角关系的过程, 理解余弦、正切、余切的意义,能够正确应用 cosA 、tanA 、cotA 表示直角三角形中两边的比; (2)通过锐角三角函数的学习,进一步认识 函数,体会函数的变化与对应的思想,逐步培 养学生会观察、比较、分析、概括等逻辑思维 能力.
【重难点预测】
1、重点:余弦、正切、余切的概念及其应用.
2、难点:理解余弦、正切、余切的意义,并 用它来表示两边的比。
一、自主学习:
自学教材第88—89页,然后回答下面问题。
1、余弦定义:在直角三角形中,锐角A 的 与 的比叫做角A 的余弦, 记作 , 即cosA =
____的 A ∠=c
;
2、正切定义:在Rt △ABC 中,∠C =90°, a 、b 分别是∠A 的对边和邻边.我们将∠A 的 与 的比叫做∠A 的______, 记作______. 即:tanA =
____的 A ∠=b
;
3、余切定义:在Rt △ABC 中,∠C =90°,
a 、
b 分别是∠A 的对边和邻边.我们将∠A 的 _____与_____的比叫做∠A 的______, 记作______. 即:cotA =
____的 A ∠=a
;
4、锐角∠A 的 、 、 、 ,统称
为锐角∠A 的三角函数.
5、Rt ΔABC 中,AB=5,AC=3,BC=4,则cosA
= ,sinA= ,tanA= cotA= 。
二、课内探究
探究点1:正弦与余弦
问题1、在Rt △ABC 中,∠C 是直角,AB=2,AC =1,分别求sinA 、sinB 、cosA 与cosB 的值。
小结:__________________________________
探究点2:正切与余切
问题2、在Rt ΔABC 中,∠C=900
,AC=4,BC=3,tanA , tanB,cotA 和cotB 的值。
小结:_______________________________________
展示点1:求出如图所示的Rt △ABC 中∠A 的四个三角函数值
展示点2、如图,在Rt △ABC 中,∠C=90°,BC=•6
,
sinA=
3
5
,求cosA 、tanB 的值.
问题3、已知tan α=3 ,α是锐角,求tan (90°- α), sin α, cos α的值。
三、拓展提升 1、在Rt △ABC 中,∠C 是直角,
5
12=AC BC , 求:sinA 与cosB 的值。
2、在Rt △ABC 中,∠C 是直角,AC=62,cosA= 1
2,
求.ABC S ∆
四、课堂小结
在Rt △BC 中,∠C=90°,我们把锐角A 的对
边与斜边的比叫做∠A 的正弦,
记作sinA ,即sinA= =a
c
. sinA =
A a A c ∠=∠的对边的斜边 把∠A 的邻边与斜边的比叫做∠A 的余弦, 记作 ,即 把∠A 的对边与邻边的比叫做∠A 的正切, 记作 ,即 把∠A 的邻边与对边的比叫做∠A 的余切, 记作 ,即
五、当堂巩固检测 1、Rt ΔABC 中, AC=1,BC=1,则cosB= ,sinA= ; 2、在直角三角形ABC 中,若三边长都扩大2倍,则锐
角A 的余弦值( )
A 、扩大2倍
B 、不变
C 、缩小2倍
D 、无法确定 3、在Rt △ABC 中,∠C =90°,AC =1,AB =3,则tanA =______,tanB =_____.
4、如图,在正方形ABCD 中, 点E 为AD 的中点,连结EB , 设∠EBA =α,
则tan α=_________.
5、亮亮沿与地面成角α的山坡走了90米,如果cos α=
3
1
,那么他上升了 米。
六、课后反思
通过这节课的学习,我提出以下几点个人的想法:
A
B C D E。