整式的乘除复习课导学案

整式的运算复习目标：掌握整式的加减、乘除，幂的运算；并能运用乘法公式进行运算。

1、掌握幂的运算法则，并会逆向运用；熟练运用乘法公式。

2、掌握整式的运算在实际问题中的应用。

一、知识梳理：1、幂的运算性质：（1）同底数幂的乘法：a m ﹒a n =a m+n （同底，幂乘，指加）逆用： a m+n =a m ﹒a n （指加，幂乘，同底）（2）同底数幂的除法：a m ÷a n =a m-n （a ≠0）。

（同底，幂除，指减）逆用：a m-n = a m ÷a n （a ≠0）（指减，幂除，同底）（3）幂的乘方：（a m ）n =a mn （底数不变，指数相乘）逆用：a mn =（a m ）n（4）积的乘方：（ab ）n =a n b n 推广：逆用， a n b n =（ab ）n （当ab=1或-1时常逆用）（5）零指数幂：a 0=1（注意考底数范围a ≠0）。

（6）负指数幂：(底倒，指反)2、整式的乘除法：（1）、单项式乘以单项式：法则：单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，其余的字母连同它的指数不变，作为积的因式。

（2）、单项式乘以多项式：m(a+b+c)=ma+mb+mc 。

法则：单项式与多项式相乘，就是根据分配律用单项式去乘多项式的每一项，再把所得的积相加。

（3）、多项式乘以多项式：(m+n)(a+b)=ma+mb+na+nb 。

多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加。

（4）、单项式除以单项式：单项式相除，把系数、同底数幂分别相除后，作为商的因式；对于只在被除式里含有的字母，则连同它的指数一起作为商的一个因式。

（5）、多项式除以单项式：().a b c m a m b m c m ++÷=÷+÷+÷多项式除以单项式，先把这个多项式的每一项分别除以单项式，再把所得的商相加。

14.1.4 整式的乘除（2）导学案学习目标：1.掌握同底数幂除法的法则，单项式、多项式除以单项式的法则，并会应用法则计算.2.探究单项式与单项式、多项式与单项式相除的算理，发展有条理的表达与思考能力.3.从探索整式除法的运算法则过程中，获取成功的体验，积累研究数学问题的经验.重点：整式除法法则的应用.难点：整式除法法则的探究.一、情境引入问题：木星的质量约是1.9×1024吨,地球的质量约是5.98×1021吨,你能算出木星的质量约为地球质量的多少倍吗?想一想：上面的式子该如何计算?二、推进新课探究1：（1）25×23=______ （2）x6·x4=_______ （3）2m×2n=________ 那么：（1）28÷23=______ （2）x10÷x6=______ （3） 2m+n÷2n=______ 猜想：a m÷a n= ? (m,n都是正整数,且m>n)同底数幂的除法: 一般地，我们有a m÷a n=_____________(a ≠0,m,n都是正整数，且m>n)法则：______________________________________.法则的推广及逆用：（1）推广：a m÷a n÷a p=_________(a ≠0,m,n,p都是正整数，且m>n+p)（2）逆用：a m-n = _____________(a ≠0,m,n都是正整数，且m>n) 想一想：a m÷a m=? (a≠0)零指数幂的性质: a m÷a m=_____，根据同底数幂的除法法则可得a m÷a m=______.性质：______________________________.符号表示： _____________(a ≠0).例：等式（x+3）0=1成立的条件是（）A. x为有理数B. x≠0C.x≠3D.x≠-3例计算：（1）x8÷ x2；（2）(ab)5÷ (ab)2.方法总结：计算同底数幂的除法时，先判断底数是否相同或变形为相同，若底数为多项式，可将其看作一个整体，再根据法则计算．探究2：计算：4a2x3·3ab2=___________; 那么：12a3b2x3÷3ab2=_____________. 单项式除以单项式的法则:_____________________________________________________________________________________________________________________. 例计算：（1）28x4y2÷7x3y；（2）-5a5b3c ÷15a4b.探究3：计算：（a+b）m=__________; 那么：（am+bm）÷ m=___________.多项式除以单项式的法则: ___________________________________________________________________________________________________________.例计算：(12a3-6a2+3a) ÷3a.方法总结：多项式除以单项式，实质是利用乘法的分配律，将多项式除以单项式问题转化为单项式除以单项式问题来解决．计算过程中，要注意符号问题.三、当堂练习1.下列算式中，不正确的是( )A．(－12a5b)÷(－3ab)＝4a4 B．9x m y n－1÷3x m－2y n－3＝3x2y2C. 4a2b3÷2ab＝2ab2 D．x(x－y)2÷(y－x)＝x(x－y)2.计算：（1）x7÷x5；（2）m8÷m8；（3）(－a)10÷(－a)7；（4）(xy)5÷(xy)3.3. 计算：（1）10ab3÷(－5ab) ；（2）－8a2b3÷6ab2；(3)－21x2y4÷(－3x2y3)；（4）(6×108)÷(3×105).4. 计算：（1）(6ab＋5a) ÷a；（2）(15x2y－10xy2) ÷5xy.四、课堂小结谈谈你本节课的收获.五、作业布置见精准作业布置单。

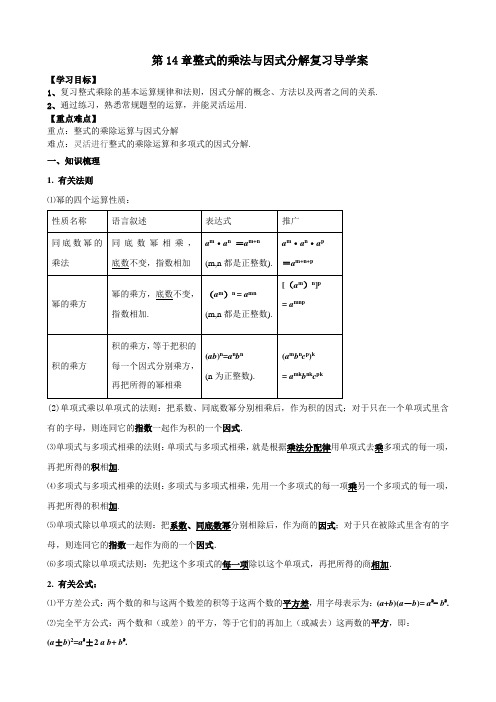
第14章整式的乘法与因式分解复习导学案【学习目标】1、复习整式乘除的基本运算规律和法则，因式分解的概念、方法以及两者之间的关系.2、通过练习，熟悉常规题型的运算，并能灵活运用.【重点难点】重点：整式的乘除运算与因式分解难点：灵活进行整式的乘除运算和多项式的因式分解.一、知识梳理1. 有关法则⑴幂的四个运算性质：(2)单项式乘以单项式的法则：把系数、同底数幂分别相乘后，作为积的因式；对于只在一个单项式里含有的字母，则连同它的指数一起作为积的一个因式．⑶单项式与多项式相乘的法则：单项式与多项式相乘，就是根据乘法分配律用单项式去乘多项式的每一项，再把所得的积相加.⑷多项式与多项式相乘的法则：多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加.⑸单项式除以单项式的法则：把系数、同底数幂分别相除后，作为商的因式；对于只在被除式里含有的字母，则连同它的指数一起作为商的一个因式．⑹多项式除以单项式法则：先把这个多项式的每一项除以这个单项式，再把所得的商相加．2. 有关公式：⑴平方差公式：两个数的和与这两个数差的积等于这两个数的平方差，用字母表示为：(a+b)(a－b)= a2- b2.⑵完全平方公式：两个数和（或差）的平方，等于它们的再加上（或减去）这两数的平方，即：(a±b)2=a2±2 a b+ b2.3. 有关概念 ⑴因式分解：把一个多项式化为几个整式的积的形式，叫做多项式的因式分解.⑵提公因式法：把多项式各项的公因式提出来，这种分解因式的方法叫做提公因式法，即am bm cm ++=m (a ＋b ＋c ).提公因式法的实质是逆用乘法分配律.⑶公式法：把乘法公式()()a b a b +-= a 2- b 2、2()a b ±= a 2±2 a b + b 2逆用，就得到分解因式的公式22a b -=(a +b )(a －b )，222a ab b ±+=(a ±b )2，这种运用公式分解因式的方法叫做公式法.（4）十字相乘法：pq x q p x +++)(2=(x +p )(x +q )。

第12章 整式的乘除§12.1.1 《幂的运算》导学案（第一课时）同底数幂的乘法学生班级： 姓名： 组别： 时间：2015年 月 日学习目标：1、在推理判断中得出同底数冪乘法的运算法则，并掌握法则的应用。

2、经历探索同底数幂的乘法运算性质的过程，感受幂的意义，发展推理能力和表达能力，提高计算能力。

3、在小组合作交流中，培养协作精神,探究精神，增强学习信心。

学习重点：同底数冪乘法运算性质的推导和应用。

学习难点：同底数冪的乘法的法则的应用。

一、自主学习，个体质疑1、（1）阅读课本P 18-19（2）32 表示几个2相乘？23表示什么？ 5a 表示什么？m a 呢？（3）把22222⨯⨯⨯⨯表示成 na 的形式？2、请同学们通过计算探索规律： （1）()()()342222222222⨯=⨯⨯⨯⨯⨯=(2)=⨯4355（3）=⨯-673)3(（4）()3111101010⎛⎫⎛⎫⎛⎫⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭（5）=⨯43a a3、比较：（1）4322⨯和 72（2）43a a ⨯和 7a (代数式表示)观察计算结果，你能猜想出 n ma a⨯的结果吗？二、小组合作，碰撞激疑问题：（1）这几道题目有什么共同特点？（2）请同学们看一看自己的计算结果，想一想这个结果有什么规律？（3）请同学们推算一下nma a ⨯的结果？同底数幂的乘法法则： 用字母表示：合作评析课后练习：（1）课本P 19页练习题1、2 （2）课本P 24页习题12.1第1题三、合作探究，师生析疑1、计算 （1） 4444⋅- （2）43)6()6(-⨯- （3）2015201622- （4）5342412523⨯+⨯-⨯2、若y x 、是正整数，且12216x y +⋅=，则 y x 、的值是什么？3、已知 28,7,4===cbam m m ，则c b a 、、之间的关系是什么？四、当堂检测，过关解疑1、计算：（1）10432b b b b ⋅⋅⋅ （2）()()876x x x -⋅-（3）()()()562x y y ---- （4）()()()3645p p p p ⋅-+-⋅-2、把下列各式化成 ()ny x + 或 ()n y x -的形式.（1）()()12+++m m y x y x （2）()()()x y y x y x ---23 3、已知 3110m m x x x +-⋅= 求m 的值.课堂反思（自主补充延伸）：§12.1.2 《幂的运算》导学案（第二课时）幂的乘方学生班级： 姓名： 组别： 时间：2015年 月 日学习目标：1、理解幂的乘方的运算性质，进一步体会和巩固幂的意义；通过推理得出幂的乘方的运算性质，并且掌握这个性质。

14 <<整式的乘除复习>>导学案一、总结反思，归纳升华1．幂的运算：同底数幂相乘文字语言：_________________________；符号语言____________. 幂的乘方文字语言： ___________________________；符号语言____________. 积的乘方文字语言： ____________________________；符号语言____________. 同指数幂相乘文字语言：_________________________；符号语言____________. 同底数幂相除文字语言：_________________________；符号语言____________.2．整式的乘除法：单项式乘以单项式： 单项式乘以多项式： 多项式乘以多项式： 单项式除以单项式： 多项式除以单项式：3．乘法公式平方差公式：文字语言___________________________；符号语言______________ 完全平方公式：文字语言________________________ ；符号语言______________4．添括号法则符号语言：二、自主探究 综合拓展1．选择题：(1)下列式子中，正确的是( )A.3x+5y=8xyB.3y 2-y 2=3C.15ab-15ab=0D.29x 3-28x 3=x(2)当a=-1时，代数式(a+1)2+ a(a+3)的值等于( )A.-4B.4C.-2D.2(3)若-4x 2y 和-2x m y n 是同类项，则m ，n 的值分别是( )A.m=2,n=1B.m=2,n=0C.m=4,n=1D.m=4，n=0(4)化简(-x)3·(-x)2的结果正确的是( )A.-x 6B.x 6C.x 5D.-x 5(5)若x 2+2(m-3)x+16是完全平方式，则m 的值等于( )A.3B.-5C.7.D.7或-12．填空：(1)化简：a 3·a 2b= .( 2)计算：4x 2+4x 2=(3)计算：4x 2·(-2xy)= .(4)按图15－4所示的程序计算，若开始输入的x 值为3，则最后输出的结果是 .三、解答题1．计算：①a ·a 3= ② (-3x)4=③(103)5= ④(b 3)4= ⑤(2b)3= ⑥(2a 3)2=⑦(m+n)2·(m+n)3=2．计算与化简.(1)(-2a 2)(3ab 2-5ab 3).(2)(5x+2y)(3x-2y) (3)(3y+2)(y-4)-3(y-2)(y-3)；（4）(-3)2008·(31)20093．先化简，再求值:(a+b)(a-2b)-(a+2b)(a-b)，其中a=2， b=-14.已知x-y=1,xy=3，求x 3y-2x 2y 2+xy 3的值.四、达标检测，体验成功（时间20分钟）1．下列各式：42x x ⋅，42)(x ，44x x +，24)(x -，与8x 相等的有（ ）A ．1个B ．2个C ．3个D ．4个2．计算：（1）=-⋅43)(a a （2）=-⋅)(45m m（3）=+⋅+53)1()1(x x （4）=+⋅+++21)2()2(n m b a b a（5）=÷310)()(ab ab （6）=-÷-35)1()1(x x（7）[]=-43)(x （8）[]=+42)1(y（9）=-343)(y x （10）()393664=-z y x（11）=⨯8825.04 （12）=⋅-20122011)23()32(3．已知5)()()(b a a b b a b a +=+⋅+，且744)()()(b a b a b a b a -=-⋅--+ 求：b a b a .4. 已知：721=+n ，求52+n 的值5. 已知310,210==n m ，求m 310，n m 2310+和n m 3210-的值6. 已知：12,2522==+mn n m ，求m+n 的值。

七年级下册第一章《整式的运算》复习学案（2课时）1、幕的运算法则：①严=（m、n都是正整数）②（/丫 =（m、n都是正整数）③(ab)"= （n是正整数）④a m^a n =（a^O, m> n都是正整数，且m>n）⑤=(aHO)®a-p =（a^O, p是正整数）例1、计算，并指出运用什么运算法则① x5-x4-x3②（-）w x（0.5）/l③（-2咼％）2(7)[伽)14- (-nni)']2• m3• n'2；(8)(方一白)"X (a—Z?)3-r (a—Z?)'；2例2、（1） 4、如果8"十4'"十2 = 16，贝I」刃的值为____（2）已知兀“ =4,兀"=9,求兀「26的值。

【巩固练习】-选择1.计算八/的结果是（）A. aB. a3C. a5D. a62.小胡图同学做了以下四个练习，你认为正确的是（）A. x2-x3 = x6B. x2+x2C.匕丹二兀曲3.设护二8 , a n =4，则（严等于（）A. 24B. 32C. 64D. 1284、小明计算（/）2值，其正确的结果是（）3 若1O21O2009 = 10,w,则沪 ___________ D. (-x)2 - x3=-x5A. a9B. a5C、a6D、a65、下列计算正确的是6、做练习题时，欢欢化简（/驱）2009 ,贝贝化简（°2009）2（炳，那么他们的化简结果（）5、如果9" = 34, 则n= ■6、计算：IO 8 一 IO?二:a m -i-a n(ni>n)=；（白+方）：＞4-（臼+〃）7、如果(a - 2)° = 二1有意义，则日应满足的条件是 ■& & =；2-J =_：1.5x10—】二（用小数表示）.109.如果 a ,l+l a 2n ~2 =a b,则 n ■10.计算：3X9X27X3"二:2"・(一8)・2"化三计算1.化简下列各题：2 202： (2) a 9-Fa 3^a ；A 、(^3)3 = a 27B 、(-X 2)2 =x 4C 、[(d + b)，丁 = (a + b )e D 、(-x)2 = -x 27、B.互为相反数C.互为倒数D- 无法比较大小如果八则应的值为（ ）8. A 、 2 B 、 3C 、4 D 、5英中正确的是（）A 、（3J4-7T ）0没有意义B 、任何数臼的零次幕都等于C 、（丄）-"二 M （QH O ） a一种计算机每秒可以运算IO?次, A 、IO 3 B 、106 C 、10、下面计算中，正确的是（ ） A 、a^a=aC 、（xy ） * （―xy ） '= （xy ） 2 填空9、1. 2. 计算：(d + l)—(Q + l)J D 、1.2X10J120它工作10 3秒可运算（ D 、1027 1012 (-2釣 B、D=x 8X (-2)/ 1 \4/ 1 X3 / i \2(1) 1• 1 . 1 : (2) a n~[ -a n -a : (3) (-x2)-(x3)-(-x)2；110丿（10丿110丿2、计算:(1)(1O2)3-1O；(2) -(a2)3-a；(3) [(x-3)2]4；(4)(2x- y)3 -(2x- y) -(2x~y)4. (5)(-a)2zf+1 x(-a)3,,+2 x(-a)(4) (m2)4-(-m)2-m (5) 3(x n)4• x2n -(x2n)33、计算:(3) (-xy) 34- (-xy) 24- (-xy)(5)(-5“)24-52n+l-?5；(6)(a-b)5 ^(b-a)3/ *7、炉2 • nrl • 3 /O、/ X 2(X)6 . zi \ 2(X)7(7)—cl —cl ；(8) (—) -r (1.5)；四应用1.我国笫五次人口普查资料表明：我国的人口约为1.3xl05,人均纯收入约为6x10-3元，请你计算当年全国人民的总收入约为多少元？2、光的速度每秒约3X1(T米，地球和太阳的距离约是1.5X10"米，则太阳光从太阳射到地球需要___________ 秒.五、逆运算1.已知川=4, x b=9,求兀点的值。

《14.1整式的乘法》复习导学案主备人：刘杨审阅人：齐丽娟年级：八年课型：复习课学习目标：1.掌握幂的运算性质和整式乘法法则并进行运算。

2.经历幂的运算性质和整式乘法法则的复习过程，体会转化、数形结合的数学思想方法，培养良好的学习习惯，增强学习的兴趣。

学习重点：幂的运算性质和整式乘法法则。

学习难点：幂的运算性质和整式乘法法则之间的联系。

导学流程：【知识回顾温故知新】问题1.请同学们回忆，幂的运算有哪些？字母表达式为：a m·a n=幂的运算字母表达式为：(a m)n=字母表达式为：(ab)n=注：上述前两个字母表达式中，-m、n有什么要求吗？针对训练：计算：（1）x·x²= (2)y5·y4·y3= (3)a m2·a2= (4)(a2)3= (5)(-x5)3= (6)(-y3)2= (7)(2a)3= (8)(-2x3)4= (9)(-3m2)3= 问题2.观察下面三个图形，请同学们用代数式分别表示它们的面积。

归纳：运算法则：整式的乘法字母表达式为：a(m+n)=字母表达式为：(a+b) (m+n)=针对训练：错题医院：（1）（31xy2）·(9x2y)2= (2)4xy(3x²y-2x+1)= (3)(a3)5-a3·a5= (4)(x-2y)(x+y)= 问题3.整式的除法分为哪几类呢？a m÷a n=整式的除法 a0= (a 0)单项式相除:法则为多项式除以单项式:法则为注：上述的字母表达式中，a、m、n有什么要求吗？针对训练：计算:(1)x 4y ²÷7x 3y= （2）-5a 5b 3c ÷15a 4b= (3)(12a 3-6a ²+3a)÷3a= (4)（-32）0= 【感悟变化 熟练运用】比一比，看谁做的又快又准！ 1. 计算：（-21x m y ）3（-4xy ²）²2. 先化简，再求值。

1 第一章整式乘除的运算复习学案 知识回顾

单项式 整 式 多项式 同底数幂的乘法 幂的乘方 积的乘方 幂运算 同底数幂的除法 零指数幂 负指数幂 整式的加减 单项式与单项式相乘 单项式与多项式相乘 整式的乘法 多项式与多项式相乘 整式运算 平方差公式 完全平方公式 单项式除以单项式 整式的除法 多项式除以单项式

一、单项式、单项式的次数： 只含有数字与字母的积的代数式叫做单项式。单独的一个数或一个字母也是单项式。 一个单项式中，所有字母的指数的和叫做这个单项式的次数。 二、多项式 1、多项式、多项式的次数、项 几个单项式的和叫做多项式。其中每个单项式叫做这个多项式的项。多项式中不含字母的项叫做常数项。多项式中次数最高的项的次数，叫做这个多项式的次数。 三、整式：单项式和多项式统称为整式。 四、整式的加减法： 整式加减法的一般步骤： （1）去括号；（2）合并同类项。 五、幂的运算性质：

1、同底数幂的乘法：am﹒an=am+n (m,n都是正整数）；

2、幂的乘方：（am）n =amn (m,n都是正整数）； 3、积的乘方：（ab）n=anbn (n都是正整数）； 4、同底数幂的除法：am÷an=am-n (m,n都是正整数,a≠0) ；

整 式 的 运 算 2

六、零指数幂和负整数指数幂： 1、零指数幂：a0=1（a≠0）; 2、负整数指数幂： p是正整数。（底倒指反，即底数

变为它的倒数，指数变为它的相反数） 七、整式的乘除法： 1、单项式乘以单项式： 法则：单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，其余的字母连同它的指数不变，作为积的因式。 2、单项式乘以多项式： 法则：单项式与多项式相乘，就是根据分配律用单项式去乘多项式的每一项，再把所得的积相加。 3、多项式乘以多项式： 多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加。 注意：同号得正、异号得负，绝对值相乘！ 4、单项式除以单项式： 单项式相除，把系数、同底数幂分别相除后，作为商的因式；对于只在被除式里含有的字母，则连同它的指数一起作为商的一个因式。 5、多项式除以单项式： 多项式除以单项式，先把这个多项式的每一项分别除以单项式，再把所得的商相加。 注意与多项式乘法相似：同号得正、异号得负，绝对值相除！ 八、整式乘法公式：

数学下册第一章整式的乘除导学案【】教案是教师对教学内容，教学步骤，教学方法等进行具体的安排和设计的一种有用性教学文书，都要通过周密考虑，精心设计而确定下来，表达着专门强的打算性。

在此小编为您整理了数学下册第一章整式的乘除导学案，期望能给教师教学提供参考。

一、学习目标：1、熟练地把握多项式除以单项式的法则，并能准确地进行运算.2、明白得整式除法运算的算理，进展有条理的摸索及表达能力.二、学习重点：多项式除以单项式的法则是本节的重点.三、学习难点：整式除法运算的算理及综合运用。

四、学习设计：(一)预习预备预习书30--31页(二)学习过程：1、探究：对比整式乘法的学习顺序，下面我们应该研究整式除法的什么内容?引例：(8x3-12x2+4x)4x=法则：2、例题精讲类型一多项式除以单项式的运算例1 运算：(1)(6ab+8b) (2)(27a3-15a2+6a)练习：运算：(1)(6a3+5a2)(-a2); (2)(9x2y-6xy2-3xy)(-3xy);(3)(8a2b2-5a2b+4ab)4ab.类型二多项式除以单项式的综合应用例2 (1)运算：〔(2x+y)2-y(y+4x)-8x〕(2x)(2)化简求值：〔(3x+2y)(3x-2y)-(x+2y)(5x-2y)〕(4x) 其中x=2,y=1练习：(1)运算：〔(-2a2b)2(3b3)-2a2(3ab2)3〕(6a4b5).(2)假如2x-y=10,求〔(x2+y2)-(x-y)2+2y(x-y)〕(4y)的值3、当堂测评填空:(1)(a2-a)(2)(35a3+28a2+7a)(7a)= ;(3)( 3x6y36x3y527x2y4)( xy3)= .选择：〔(a2)4+a3a-(ab)2〕a = ( )A.a9+a5-a3b2B.a7+a3-ab2C.a9+a4-a2b2D.a9+a2-a2b2运算:(1)(3x3y-18x2y2+x2y)(-6x2y); (2)〔(xy+2)(xy-2)-2x2y2+4〕(xy).4、拓展：(1)化简; (2)若m2-n2=mn,求的值.回忆小结：多项式除以单项式，先把那个多项式的每一项分别除以单项式，再把所得的商相加。