Xr看到(实验)至r次成功为止.
- 格式:doc
- 大小:40.50 KB
- 文档页数:2


策略5 精推细敲,稳做遗传变异高考压轴题【名师献策】遗传变异作为高考压轴题是全国卷及各省市卷的必然选择,100%考,仅2012高考全国新课标卷、大纲卷加十个省市单独命题卷涉及的遗传变异大题就有13个综合大题。
命题集中在以下六个方面:1.应用遗传规律进行遗传现象的解释、基因型的推断、概率的计算;2.基因在染色体上位置的确认及遗传的内在规律;3.变异及其原理在实践中的应用;4.人类遗传病及系谱图分析;5.以中心法则为中心分子基础题;6.遗传(变异)类实验设计及探究。
不管侧重考哪一方面,试题普遍综合性强,难度系数高。
【考题例证1】(2012·新课标理综,31)一对毛色正常鼠交配,产下多只鼠,其中一只雄鼠的毛色异常。
分析认为,鼠毛色出现异常的原因有两种:一是基因突变的直接结果(控制毛色的基因显隐性未知,突变只涉及一个亲本常染色体上一对等位基因中的一个基因);二是隐性基因携带者之间交配的结果(只涉及亲本常染色体上一对等位基因)。
假定这只雄鼠能正常生长发育,并具有生殖能力,后代可成活。
为探究该鼠毛色异常的原因,用上述毛色异常的雄鼠分别与其同一窝的多只雌鼠交配,得到多窝子代。
请预测结果并作出分析。
(1)如果每窝子代中毛色异常鼠与毛色正常的鼠比例均为________,则可推测毛色异常是________性基因突变为________性基因的直接结果,因为__________________________________________________________________。
(2)如果不同窝子代出现两种情况,一种是同一窝子代中毛色异常鼠与毛色正常鼠比例是________,另一种是同一窝子代全部表现为________鼠,则可推测毛色异常是隐性基因携带者之间交配的结果。
解析该题以常染色体上一对等位基因控制生物的性状为出发点,结合基因突变,考查对遗传规律和生物变异的分析应用能力,难度较低。
假设该性状由一对等位基因Aa控制;(1)若为基因突变,又只涉及一个亲本常染色体上一对等位基因中的一个基因,要想表现毛色异常,该突变只能为显性突变,即由隐性基因突变为显性基因,突变体为Aa,正常雌鼠为aa,所以后代毛色异常鼠与毛色正常鼠的比例均为1∶1;(2)若为亲本中隐性基因的携带者,此毛色异常的雄鼠(基因型为aa)与同一窝的多只雌鼠(基因型为AA或Aa)交配后,不同窝的子代不同,若雌鼠为AA,后代全部为毛色正常鼠,若雌鼠为Aa,后代毛色异常鼠与毛色正常鼠的比例是1∶1。

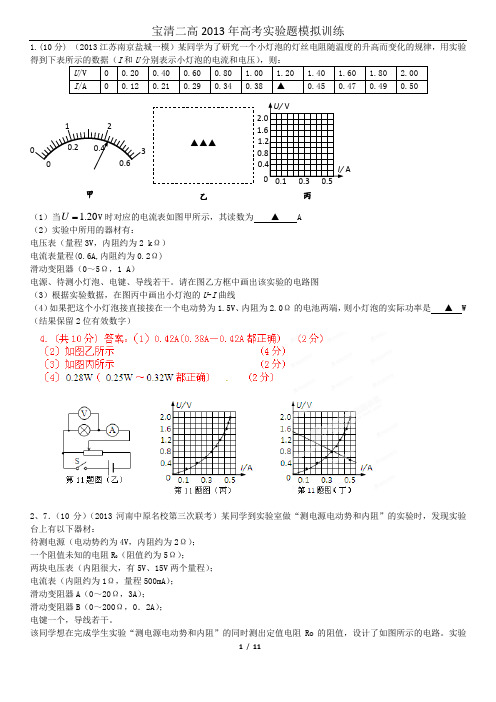
1.(10分) (2013江苏南京盐城一模)某同学为了研究一个小灯泡的灯丝电阻随温度的升高而变化的规律,用实验得到下表所示的数据(I 和U 分别表示小灯泡的电流和电压),则:(1)当20.1 U V 时对应的电流表如图甲所示,其读数为▲A (2)实验中所用的器材有:电压表(量程3V ,内阻约为2 k Ω) 电流表量程(0.6A,内阻约为0.2Ω) 滑动变阻器(0~5Ω,1 A )电源、待测小灯泡、电键、导线若干。
请在图乙方框中画出该实验的电路图 (3)根据实验数据,在图丙中画出小灯泡的U -I 曲线(4)如果把这个小灯泡接直接接在一个电动势为1.5V 、内阻为2.0Ω的电池两端,则小灯泡的实际功率是▲W (结果保留2位有效数字)2、7.(10分)(2013河南中原名校第三次联考)某同学到实验室做“测电源电动势和内阻”的实验时,发现实验台上有以下器材:待测电源(电动势约为4V ,内阻约为2Ω); 一个阻值未知的电阻R 0(阻值约为5Ω);两块电压表(内阻很大,有5V 、15V 两个量程); 电流表(内阻约为1Ω,量程500mA ); 滑动变阻器A (0~20Ω,3A ); 滑动变阻器B (0~200Ω,0.2A ); 电键一个,导线若干。
该同学想在完成学生实验“测电源电动势和内阻”的同时测出定值电阻Ro 的阻值,设计了如图所示的电路。
实验时他用U 1、U 2、I 分别表示电表V l 、V 2、A 的读数。
在将滑动变阻器的滑片移动到不同位置时,记录了U 1、U 2、I 的甲 A乙丙一系列值.其后他在两张坐标纸上各作了一个图线来处理实验数据,并计算了电源电动势、内阻以及定值电阻Ro 的阻值。
根据题中所给信息解答下列问题:(1)在电压表Vl接入电路时应选择的量程是,滑动变阻器应选择(填器材代号“A’’或“B”);(2)在坐标纸上作图线时,用来计算电源电动势和内阻的图线的横坐标轴、纵坐标轴分别应该用、表示;用来计算定值电阻Ro的图线的横坐标轴、纵坐标轴分别应该用、表示。

2025届高三11月教学质量测评物理本试题卷共6页。
全卷满分100分。
考试用时75分钟。
祝考试顺利注意事项:1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内。
写在试卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试卷和答题卡一并上交。
一、选择题:本题共10小题,共46分。
在每小题给出的四个选项中,第1~7题只有一项符合题目要求,每小题4分;第8~10题有多项符合题目要求,每小题6分,选对但不全的得3分,有选错的得0分。
1.如图,有一匀强电场的电场强度方向与圆所在平面平行,圆的半径,圆周上的3个点a 、b 、c 的电势分别为其中ab 为圆的直径,,则该匀强电场电场强度大小为( )A .B .C .D .2.一静止的铀核放出一个粒子衰变成钍核,衰变方程为。
下列说法正确的是( )A .α射线的穿透能力比射线强B .高温下的半衰期变短C .铀核的质量大于粒子与钍核的质量之和D .比的比结合能大3.如图所示,由紫光与红光混合的细光束从底面镀银的半圆形玻璃砖顶点A 以入射角射入玻璃砖,1m R =0,126,a b c V V ϕϕϕ===、60cab ∠=︒/m E=/m E =12V /m E=/mE =α238234492902U Th He →+γ23892U α23892U 23490Th 60θ=︒已知该玻璃砖对紫光与红光的折射率分别为,光束在玻璃砖半圆弧面上发生折射时不考虑反射,紫光与红光在玻璃砖内传播的时间分别为。
下列判断正确的是( )A .B .C .D .4.如图所示,卫星a 、b 沿圆形轨道绕地球运行,a 是极地轨道卫星,卫星b 轨道平面与地球赤道平面重合,此时两卫星恰好经过地球赤道上P 点的正上方。

实验23 磺基水杨酸铁(Ⅲ)配合物的组成及K稳的测定[实验目的]1、了解分光光度计测定配合物组成及K稳的原理和方法。
2、测定PH<2.5时磺基水杨酸铁(Ⅲ)的组成及K稳。
3、练习使用分光光度计。
[实验原理]磺基水杨酸(HO SO3H,简式H3R)与Fe3+可形成稳定的配合物,因溶液PH值不同,其组成也不相同。
本实验测PH<2.5时所形成红褐色磺基水杨酸铁(Ⅲ)配离子的组成及K稳。
实验中用HClO4溶液来控制PH值。
1、分光光度法测定配合物组成的基本原理:①用透光率T表示:即透光的强度I t与入射光强度I0之比。
T=I t/I0②用吸光度D表示(又称消光度、光密度),它是透光率的负对数:D=-lgT=lgI0/I tD值大表示光被有色溶液吸收的程度大:反之亦然。
2、朗伯—比尔定律D=ε c L即:一束单色光通过有色溶液时,有色溶液的吸光度与溶液的浓度c和液层厚度L乘积成正比(ε为消光系数,λ0一定时,ε为特征常数)。
3、可行性论证所测溶液中,H3R为无色,Fe3+溶液的浓度很稀,也可认为无色,只有MR x是有色的(磺基水杨酸铁(Ⅲ)配离子为有色)。
因此,溶液的吸光度D只与配离子浓度成正比。
通过对溶液吸光度的测定,可以求出该配离子的组成。
4、配离子组成的求得(分光光度法求时,常用的两种方法):①等摩尔系列法(连续变化法,本实验采用此法):保持(n M+n R)不变的前提下,使M和R的摩尔分数连续变化而配制一系列溶液,显然,这些溶液中必有一种物质过量,配离子浓度不可能达最大。
只有当溶液中M与R的物质的量之比与配离子组成一致时,C MRx才最大。
MR x的浓度增大,溶液颜色加深,D增大。
若x值,如图1:=n R/n总=0.5=n M/n总=0.5x值=x R/x M=1(图1)中心离子摩尔分数由图1可以看出x=1,该配合物组成为MR,最大吸光度A点可以认为是M和R全部形成配合物时的吸光度,其值为D1,由于部分离解,其浓度要稍小一些,所以实测吸光度为B点,其值为D2,因此配离子的离解度〆可表示为:〆=(D1-D2)/D1再由1:1组成关系,即可求出表观稳定常数Kˊ,M + R == MR平衡时c〆c〆c-c〆Kˊ=[MR]/([M][R])=(1-〆)/c〆2(式中C为相应于A点的金属离子M的浓度)考虑弱酸的电离平衡,对Kˊ加以校正,校正后得K稳:lgK稳=lg Kˊ+lgθ(θ为酸效应系数)(对于H3R,PH=2时,lgθ=10.2)应该指出:该法应用于研究络合比高或离解度较大的络合物,得不到准确的结果。
约瑟夫问题实验报告(文章一):约瑟夫问题数据结构实验报告中南民族大学管理学院学生实验报告实验项目: 约瑟夫问题课程名称:数据结构年级:专业:信息管理与信息系统指导教师:实验地点:管理学院综合实验室完成日期:小组成员:学年度第(一)、实验目的(1)掌握线性表表示和实现;(2)学会定义抽象数据类型;(3)学会分析问题,设计适当的解决方案;(二)、实验内容【问题描述】:编号为1,2,…,n 的n 个人按顺时针方向围坐一圈,每人持有一个密码(正整数)。
一开始任选一个正整数作为报数上限值m,从第一个人开始按顺时针方向自 1 开始顺序报数,报到m 时停止报数。
报m 的人出列,将他的密码作为新的m 值,从他在顺时针方向上的下一个人开始重新从1 报数,如此下去,直至所有人全部出列为止。
试设计一个程序求出出列顺序。
【基本要求】:利用单向循环链表存储结构模拟此过程,按照出列的顺序印出各人的编号。
【测试数据】:m 的初值为20;密码:3,1,7,2,4,8,4(正确的结果应为6,1,4,7,2,3,5)。
(三)、实验步骤(一)需求分析对于这个程序来说,首先要确定构造链表时所用的方法。
当数到m 时一个人就出列,也即删除这个节点,同时建立这个节点的前节点与后节点的联系。
由于是循环计数,所以才采用循环列表这个线性表方式。
程序存储结构利用单循环链表存储结构存储约瑟夫数据(即n个人的编码等),模拟约瑟夫的显示过程,按照出列的顺序显示个人的标号。
编号为1,2,?,n 的n 个人按顺时针方向围坐一圈,每人持有一个密码(正整数)。
一开始任选一个正整数作为报数上限值m,从第一个人开始按顺时针方向自1 开始顺序报数,报到m 时停止报数。
报m 的人出列,将他的密码作为新的m 值,从他在顺时针方向上的下一个人开始重新从1 报数,如此下去,直至所有人全部出列为止。
试设计一个程序求出出列顺序。
基本要求是利用单向循环链表存储结构模拟此过程,按照出列的顺序印出各人的编号。
§negative binomial random variable
Xr:看到(實驗)至r次成功為止,所經歷之試驗次數
社每次成功之機率為P
則P(Xr=k)= k-1 。P。P。…P。(1-P) 。(1-P)= k-1 P的r次方q的k-r次方.k=r.r+1…
r-1 r-1
認知(∞Σk-r)P的r次方q的x-r次方=1
為何稱他為二項: (a+b)的n次方.nεN
展開=(nΣk=0) n a的k次方b的n-k次方 or (nΣk=0) n
a的n-k次方b的k次方
k k
P=1(1-P)
P的-r次方=(1-(1-p))的-r次方:負二項展開式=Σ –r 1的-r-k次方(-(1-p))的k次方
K
整理 -r =(-r)(-r-1)…(-r-k+1)/k!=(-1)的k次方((r+k-1)(r+k-2)…r)/k!
k
=(-1)的k次方(r+k-1)(r+k-2)…(r+1)r(r-1)!/k!(r-1)!=(-1)的k次方r+k-1
r-1
所以P的-r次方=Σ(-1)的k次方 r+k-1 (-1)的k次方(1-p)的k次方
r-1
=Σ r+k-1 (1-p)的k次方
r-1
所以p的r次方p的-r次方=Σr+k-1 p的r次方(1-p)的k次方
r-1
=(∞Σw>r) r+k-1 p的r次方(1-p)的k次方
r-1
另w=r+k→(∞Σw>r) w-1 p的r次方q的w-r次方
r-1
§poisson random variable
特點:若一時段中發生事件屬稀少性
在[0.t]發生事件數記x[0.t]則Pr(X[0.t]=k)=e的-λt次方(-λt)的k次方/k!
其中λ:平均次數/單位時間
EX:某航空公司飛航事故屬poisson分配
另λ=3次/5年事故 球再某一年終洽發生2個事故之機率?
Sol:設X[0.t]:一年中發生事故數
所以Pr(X[0.t]=2)=e的-3/5-1次方((3/5)1)的平方=e的-3/5次方(0.6)平方/2!
基本假設:
(1) 在極短時間X[t.t+Δt]內發生2次以上(含)之機率為0(Δt) IF an=0(bn)即表
Lim n→∞ an/ bn=0
(2) 在Δt內發生1個事件之機率與Δt成正比: λΔt
(3) 在不同兩時段發生事件彼此獨立
(4) 事件之發生僅與時間長短有關與起始時間無關 則P(X[0.t]=k)= e的-λt次方
(-λt)的k次方/k!
Sol:let Pn(t)=P(X[0.t]=n)
Pn(t+Δt)=P(X[0.t+Δt]=n)=Pn(t)P0(Δt)+ Pn-1(t)P1(Δt)+ Pn-2(t)P2(Δt)…P0(t)Pn(Δt)]
→Pn(t+Δt)= Pn(t) P0(Δt)+ Pn-1(t) P1(Δt)+0(Δt)
Pn(t+Δt)= Pn(t) P0(Δt)+ Pn-1(t)λΔt+0(Δt)= Pn(t)(1-λΔt-0(Δt))+ Pn-1(t) λΔ
t+0(Δt)
Pn(t+Δt)= Pn(t)(1-λΔt)+ Pn-1(t) λΔt-0(Δt)
Pn(t+Δt)- Pn(t)=-λPn(t) Δt+λPn-1(t)Δt+0(Δt)= -λΔt {Pn(t)- Pn-1(t)}+ 0(Δt)
兩邊同除以Δt lim Δt→0 Pn(t+Δt)- Pn(t)/Δt=-λ{Pn(t)- Pn-1(t)+ lim Δt→0 0(Δ
t)/Δt=0
Pn(t)=-λ{Pn(t)- Pn-1(t)}
1問Pn(t)=? 當n=0 帶入1 P0(t)= -λ(P0(t)- P-1(t))
P-1(t)=0 P0(t)= -λP0(t) P0(t)/ P0(t)= -λ 左式 d/nP0(t)/Δt=-λ
所以dln P0(t)=- λΔt
兩邊積分∫dln P0(t)=ln P0(t)=∫-λt+C
所以P0(t)=e的-λt+C次方 t=0帶入P0(0)=1=e的0+c次方
所以c=0
所以P0(t)=e的-λt次方
P0(t)=e的-λt次方(λt)的0次方/0!=e的-λt次方
N=1時P1(t)= -λt(P1(t)- P0(t)) P1(t)+ λP1(t)= λP0(t)=-λe的-λt次方
兩邊同乘以積分因子e的∫λdt次方=e的λt次方