当前位置：文档之家 › 保险精算中的人寿保险的精算现值的模型

保险精算中的人寿保险的精算现值的模型

  • 格式：docx
  • 大小：200.28 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

第二章人寿保险的精算现值

第二章人寿保险的精算现值
第二ቤተ መጻሕፍቲ ባይዱ人寿保险的精算 现值
2020年4月23日星期四
人身保险是以人的寿命和身体为保险标的的保险。
人寿保险是人身保险的一种。
人寿保险转嫁的是被保险人的生存或者死亡的风险 。它起源于古代的互助团体，其原理是通过集合具 有同质风险的大量被保险人，通过在这些被保险人 之间进行风险分散——即由所有的被保险人共同出 资给遭遇风险的少数被保险人——来达到降低突发 风险事故对遭遇风险事故的个体造成的财务冲击。
2020/4/23
第二章 人寿保险的精算现值
• 解 : 设 Zj 表示第 j 个被保险人的死亡给付在投保时的现值随机变量 , 则
勇于开始，才能找到成 功的路
2020/4/23
第二章 人寿保险的精算现值
设该项基金在最初时的数额至少是 h 元 , 依题意 , 则
勇于开始，才能找到成 功的路
即该项基金在最初时的数额至少要有 449.35 元 , 比所收取的 建缴纯保费建立的初始基金 400(=100 × 4) 元多出 49.35 元 , 即超过歪缴纯保费基金的 12.34% 。这说明 , 最初基 金 需有风险附加费 ( 即安全附加费 ) 的存在 , 即该基金超过保费 总额的那部分 (49.35 元 ) 是 安全附加基金。
1. 按算术数列续年递增的终身寿险 按算术数列{n} 续年递增的连续型的终身寿险 , 可分
称现值函数随机变量Z的数学期望为保险的精算现值，也是趸缴纯保费额
于是
2020/4/23
第二章 人寿保险的精算现值
则连续型的保险金额为 1 个单位的 n 年定期寿险
现值随机变量 ZT 的方差是
勇于开始，才能找到成 功的路
2020/4/23
第二章 人寿保险的精算现值

第二章 人寿保险的精算现值PPT课件

第二章 人寿保险的精算现值PPT课件

2.4 换算函数
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
Thank You
在别人的演说中思考，在自己的故事里成长
Thinking In Other People‘S Speeches，Growing Up In Your Own Story
讲师：XXXXXX XX年XX月XX日
微分方程
2.2 离散型保险
等额保险
定期死亡保险 终身寿险 两全保险 延期保险
变额保险
递增保额保险 递减2.3 连续型保险与离散型保险之间的关 系
前面两节的讨论表明，离散型保险的趸缴纯 保费的计算要容易和简便很多，可编制如P467 的终身寿险精算现值表，而实务中使用的是连 续型保险，因而寻找连续型保险与离散型保险 之间的关系是有意义的。
变额保险
递增保额保险 递减保额保险
微分方程
等额保险
所谓等额保险，指保险利益的金额在保险 开始时就已经固定，只是支付的时间不确 定而已，支付时间与保险事故发生的时间 有关。
P59 2，11
作业
P59 4
作业
变额保险
变额保险，顾名思义，是指保险利益不是常 数，而是随着死亡发生的时间不同而不同的 保险。
第二章 人寿保险的精算现值
学习目标
熟悉人寿保险的数学模型 熟悉人寿保险现值随机变量及人寿保险精
算现值 掌握各种寿险产品趸缴净保费及人寿保险
现值随机变量方差的计算方法 了解趸缴净保费的实际意义及递推公式 熟悉利用换算函数计算人寿保险的趸缴净

人寿保险的精算模型及应用

人寿保险的精算模型及应用

人寿保险的精算模型及应用人寿保险的精算模型及应用人寿保险精算模型是保险公司用来评估和管理风险的工具，它帮助保险公司确定保险费率、保单赔付金额以及其他相关事项。

下面将介绍人寿保险精算模型的应用步骤。

第一步：数据收集人寿保险精算模型的建立需要大量的数据支持。

保险公司会收集各类与保险相关的数据，包括被保险人的年龄、性别、健康状况、职业等信息，以及历史的理赔数据和保单数据。

这些数据将作为模型的输入，用于进行风险评估和预测。

第二步：建立概率模型在收集到数据后，保险公司会使用概率模型来计算不同风险事件的概率。

这些事件可以包括被保险人的死亡、疾病或意外事故等。

概率模型通常使用各类统计方法和数学公式来估计事件发生的概率，以及事件发生后的理赔金额。

第三步：模型验证与调整建立概率模型后，保险公司会使用历史数据对模型进行验证。

他们会将模型预测的结果与实际情况进行比较，评估模型的准确性和可靠性。

如果发现模型存在偏差或误差，保险公司会进行相应的调整和改进，以提高模型的预测能力。

第四步：风险评估与定价通过建立概率模型，保险公司可以对不同风险事件的概率进行评估，并据此确定保险费率和理赔金额。

根据模型预测的结果，保险公司可以制定具有竞争力的保险产品，并确保公司在面临风险时能够获得适当的收益。

第五步：风险管理和监控人寿保险精算模型的应用不仅用于确定保险费率和理赔金额，也用于风险管理和监控。

保险公司可以使用模型来评估和监控风险的变化，及时采取相应的措施进行风险管理。

模型还可以帮助保险公司确定资本需求和盈利能力，以支持公司的可持续发展。

总结：人寿保险精算模型是保险公司进行风险评估和管理的重要工具。

通过数据收集、建立概率模型、模型验证与调整、风险评估与定价以及风险管理和监控这一系列步骤，保险公司可以更好地理解和管理风险，同时提供具有竞争力的保险产品。

保险精算模型的应用对于保险行业的可持续发展至关重要。

第4章 人寿保险的精算现值

第4章 人寿保险的精算现值

第4章 人寿保险的精算现值人寿保险的精算现值也称为趸交纯保费。

4.2 死亡年末给付的人寿保险死亡年末给付的人寿保险是指保险金的支付是在死亡发生的（保险期）年末进行的人寿保险。

4.2.1 定期寿险的趸交纯保费设)(x 投保n 年期定期寿险，保险金额为1元，保险金在死亡年度末给付。

设K = ][T ,即取整余命随机变量，给付函数用b K 1+表示，则有 b K 1+ = 1，当K = 0，1，2，…，n-10, 其它相应的贴现因子用v K 1+表示，保险金给付额折换成购买保险合同签单时的现值用随机变量Z 表示。

Z 的可能取值为z K 1+（K = 0，1，2，…，n-1）z K 1+ = v b K K 11++⋅ = vK 1+定期寿险的趸交纯保费用统一的精算符号1x n A 表示，那么1x nA= )(Z E =∑-=++⋅⋅11n k kx xk qp vk)(Z Var = )]([22)(ZE Z E -=2211()x nx nAA-其中 21x nA= )(2Z E = ∑-=++⋅⋅1)1(2n k kx xk qp vk4.2.2 生存保险n 年期生存保险是当被保险人生存至n 年期满时，保险人在第n 年年末支付保险金的保险。

设)(x 投保n 年期生存寿险，保险金额为1元，保险金在第n 年年末给付。

精算中用1x nA表示该生存保险的趸交纯保费。

可以推出1x nA=pvnxn⋅相应的方差为)(Z Var = )]([22)(Z E Z E - = 2112()x nx n A A-= q pvn nxxn⋅⋅24.2.3 终身寿险的趸交纯保费Ax=1lim x nn A→∞=∑∞=++⋅⋅1k kx xk qp vk相应的方差为)(Z Var = )]([22)(ZE Z E -= )(22A Ax x-4.2.4 两全保险的趸交纯保费设)(x 投保n 年期两全保险，保险金额为1元，若)(x 在n 年内死亡，则在死亡年末给付保险金，若)(x 生存满n 年，则在第n 年年末支付满期保险金。

第二章： 人寿保险的精算现值(趸缴纯保费)

第二章： 人寿保险的精算现值(趸缴纯保费)

fT
(t)
1（均匀分布） 70
A1 30:10
10 t
0
fT
(t)dt
10 (1 0.1)t 1 dt 1
0
70 70
10 (1.1)tdt 0.092099
0
A 2 1
（2） 30:10
10 2t
0
fT
(t)dt
1 70
10 (1.1)2tdt 0.063803
0
Var(Z) 2A1 (A1 )2 0.055321
A1 xm:n
A1 x:m
Ax
1 m:n
A1 x:m
A xm:n
例 3．设生存函数 s(x) 1 x , (0 x 100) ，年利率 i 0.1，保额 1。 100
计算：（1）
A1 30:10
（2）Var(Z )
解：（1）
fT
(t)
s(x t) s(x)
1 100
x
,
代入
x 30 ,
Ax E(T ) E( K S ) E( K 1S1)
E( K 1)E( S1) Ax E[(1 i)1S ]
S ~U (0,1) Ax
1(1 i)1s ds i
0
Ax
例1． 证明：在 UDD 假设下： A1 i A1
x:n
x:n
证明：
A1 x:n
n
t
0
t
px xt dt
（1）
m m px
n
t
0
t
pxmxmt dt
A1 x:m
A1 xm:n
A1
（2） m x:n
mn mn px
m m px n n pxm

第四章 人寿保险的精算现值(.3.27)共91页文档

第四章 人寿保险的精算现值(.3.27)共91页文档
已知未来给付的现值，再考虑该给付发生的概 率，就可以得出期望给付额
E(Zt)E(bK1vK1)＝ Zt.kqx E(Zt)E(bTvT) Zt.fT(t)dt
寿险精算
8
这个期望给付就等于被保险人的趸缴纯保费 也就是精算现值，即
精算现值＝ E ( Z t )
净均衡原理并不是指每个被保险人个人缴 纳的净保费恰好等于他个人得到的保险给 付金额。它的实质是把相同风险的人视作 一个总体，这个总体在统计意义上的收支 平衡
寿险精算
9
§4.1 死亡即付的人寿保险
• 死亡即刻赔付就是指如果被保险人在保障 期内发生保险责任范围内的死亡，保险公 司将在死亡事件发生之后，立刻给予保险 赔付。它是在实际应用场合，保险公司通 常采用的理赔方式。
• 由于死亡可能发生在被保险人投保之后的 任意时刻，所以死亡即刻赔付时刻是一个 连续随机变量，它距保单生效日的时期长 度就等于被保险人签约时的剩余寿命。
连续型寿险
寿险精算
10
主要险种的精算现值（趸缴纯保费）的厘定 1.n年定期保险 2.终身保险 3.生存保险 4.n年期两全保险 5.延期寿险 ——延期m年的终身保险 ——延期m年的n年定期保险 ——延期m年的n年期两全保险
寿险精算
11
一、n年定期保险的精算现值
1.定义——什么是定期保险
2.基础模型假定条件
寿险精算
5
• 为了解决以上问题，趸缴净保费的厘定给 出了以下三条假设：
假定一：同性别、同年龄、同时参保的被保 险人的剩余寿命独立同分布 假定二：被保险人的剩余寿命分布可以用经 验生命表进行拟合 假定三：保险人可以预测将来的投资收益
这三条假定将单个被保险人的风险事故转 化为一个同质总体的风险事故

保险精算第4章(3)

保险精算第4章(3)

i=10%，求这一保单的精算现值。
64
解： 20000 A40 20000 vk1 q k| 40 20000 vk1 k|q40
k0
k0
q k| 40
k
p40 q40k
l40k l41k l40
1 ,(0 k 65) 65
于是20000
A40
20000
64
（
1
）k + 1
4
一、终身寿险
模型：(x)，bk 1, k 0,1, ,贴现函数vk1 于是 Zk 1 vk1; k 0,1, ,
精算现值E(Zk ) vk1 k|qx k0 记为 Ax
5
Ax表示x岁投保，保险金额为1个单位的终身寿险， 并在死亡年度末给付的保单的精算现值。
A v q x
k0
k 1 k|
x
v k 1
k0
dxk lx
lx Ax v k1d xk k0
表明：lx在 x 投保终身寿险的趸缴纯保费总额正好
等于生命表中在死亡年度末死亡人数的单位赔付。
6
例4.8：某人在40岁时买了保险额为20000元的终身
寿险，死亡年度末给付，假设他的生存函数可以表示
为
x
lx
1000
(1
) 105
4
解：
1000
A1 55:5|
50000
v k 1 k p55 q55k
k0
1000
k
4
0
1 1.06
k
1
l55 k l55
l55k l55k 1 l55 k
1000
k
4 0
1 1.06
k

保险精算学寿险精算现值

保险精算学寿险精算现值

1 D x
M
t 0

x t
引进转换函数：Rx M x t
t 0

则 IA x
Rx Dx
根据概率的知识，我们还可以得到
IA x E Z (k 1)v
k 0

k 1 k
qx k Ax
k 0

（2）定期递增寿险
用 IA x:n 表示趸缴净保费，则
631终身寿险年缴净保费死亡年末赔付单位元终身寿险如果规定保费每年一次终身交付这时保险费的现值就是终身生存年金精算现值以表示年缴均衡净保保费在年内缴清632定期寿险年缴净保费在死亡均匀分布的假设下如果被保险人死亡瞬时赔付633两全寿险年缴净保费634延期年金年缴净保费延期年的终身生存年金的年缴净保费设保费的缴付期限为表示年缴净保费
k 0
本节介绍当保险金随保险时期按等差数列变动时的现值表达式。 （1）递增型人寿保险的趸缴净保费 （2）递减型人寿保险的趸缴净保费
（1）标准递增终身寿险
某x岁的人投保，保单规定，若被保险人在第一年死亡，保险金为1单 位元；若被保险人在第二年内死亡，保险金为2单位元 用 IA x 表示这种保险的现值，则
IA x:n IA x:n
1
nAx:n 1
（4） 等值递增n年的终身寿险的趸缴净保费
用 I n A 表示趸缴净保费，则
I A IA
n x t n
x
x
n IA x
t 1 其中， IA ( t n 1) v q x t x n
2 2 2n p v p v n x n x n p xn qx . n 2
Z Z1 Z 2

精算学在人寿保险精确定价中的模型与实践

精算学在人寿保险精确定价中的模型与实践

精算学在人寿保险精确定价中的模型与实践人寿保险作为保险业中的重要领域之一，对于公司的盈利和长期稳定运营具有至关重要的意义。

在人寿保险的核心业务中，精确确定保险产品的定价是一项关键任务。

而精算学作为一门应用统计学和数学的学科，为人寿保险定价提供了重要的模型与实践支持。

一、精算学的基本概念与方法精算学是一门研究利用数理统计和数学方法对保险业务进行定价、风险评估和资金管理的学科。

它通过对于保险产品中的风险分析、风险评估以及赔付管理等方面进行系统的研究与分析，为人寿保险公司提供可靠的决策依据。

在人寿保险精确定价中，精算师首先需要对于保险产品的风险进行评估。

这包括数据的收集与整理，以及对于数据的统计分析，了解客户群体的特征、发生概率等重要信息。

然后，通过运用数学模型和理论，建立与优化定价模型，根据风险评估和资金管理的需求，进行定价方案的制定和调整。

最后，在实际销售过程中，根据市场需求和产品特点，进行营销和销售渠道的选择。

二、精算学在人寿保险精确定价中的模型精算学在人寿保险定价中应用广泛的模型包括：生命表模型、风险评估模型、赔付管理模型等。

其中，生命表模型作为人寿保险中常用的模型之一，用于估计不同年龄段人口的死亡概率。

通过对不同年龄段的死亡概率进行建模和分析，可以评估保险公司需要支付的保险赔付金额，从而确保产品定价的合理性。

风险评估模型是另一个重要的精算模型。

它通过对客户的风险特征进行评估，包括年龄、健康状况、职业等因素的综合考虑，来确定保险产品的定价。

通过风险评估模型，保险公司可以更准确地估计客户的风险水平，从而制定出更合理的保险费用。

赔付管理模型是在精算学中用于管理保险公司赔款的重要模型。

通过对保险理赔数据的分析和建模，可以识别出异常水平的理赔案件，并采取相应措施进行管理和控制。

赔付管理模型的应用可以帮助保险公司合理控制理赔风险，保证公司的盈利能力和可持续发展。

三、实践中的精算学在人寿保险精确定价中的应用在实践中，精算学在人寿保险精确定价中的应用是充分发挥的。

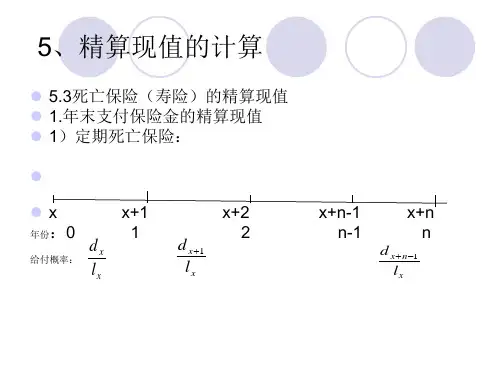
保险精算课程三(寿险精算)

保险精算课程三(寿险精算)
1000 M 20 M 40 D40 D20
课堂练习：某人30岁投保，被 保险人在开始5年内死亡，给付 1000元，5年以后死亡，给付
2000元，求趸缴纯保险费。
2000A30
1000
A1 30:5|
2000 M 30 1000 M 30 M 35
D30
D30
2.随时支付保险金的寿险的精算现值
5、精算现值的计算
5.3死亡保险（寿险）的精算现值 1.年末支付保险金的精算现值 1）定期死亡保险：
x 年份：0 d 给付概率： x
lx
x+1 1
x+2 2
d x1 lx
x+n-1 n-1
x+n n
d xn1 lx
lx
A1 x:n |
dx
v d x1 v2
d xn1 vn
A1 x:n |
h P(ax )
ax a
x:h|
Nx
Nx Nxh
5.N年定期年金
h P(ax：n| )
ax:n| ax:h|
Nx Nx
N xn N xh
6.限期缴费延期终身年金
h P(m|ax )
m| ax ax:h|
N xm Nx Nxh
h P(m| ax )
m| ax ax:h|
N xm1 Nx Nxh
t
px
xt
dt
M x M x1
Rx Dx
2）递增定期变额寿险
（IA)1x:n|
n
[t
0
1]v t
t
px
xt
dt
R x Rxn nM xn Dx
标准递增期初付终身生存年金

保险精算 第4章2 人寿保险的精算现值

保险精算 第4章2 人寿保险的精算现值
k 0 n 1
例6
55岁的男性投保5年期的定期保险，保险金额为 1000元，保险金在死亡年末给付，按中国人寿保险 业 经验生命表 （2000-2003年）非养老业务男表和利率 6%计算趸缴纯保费。 4 d 55k 1 k 1 1000 v 解：A55: 5| l k 0
55
vd55 v d 56 v d 57 v d 58 v d 59 1000 l55
2 3 4 5
26.981485(元)
注：
令n 1, 在符号Ax1: n|中， Ax1: 1| 在人寿保险中又称为自然保费， 或记作符号 c x
根据每一保险年度，每一被保险人当年年龄的预 定死亡率计算出来的该年度的死亡纯保费。 1 dx cx vqx 1 i lx “均衡保费制”
n年定期寿险的趸缴纯保费
基本函数关系 记 K ( x) [T ] k 为被保险人的取整余命，则
保险金给付在签单时的现值随机变量为
v , Z bK vK 0,
K 1
K 0,1,, n 1 其他
A1 x:n 表示其趸缴纯保费。
则
E ( Z ) v k p x q xk
T v , T n 0, T n 其中Z1 , Z2 n 0, T n v , T n
Z1 Z 2 0
1 Var(Z ) Var(Z1 ) Var(Z2 ) A1 A x：n| x：n|
延期m年的n年期两全保险
定义 保险人对被保险人在投保m年后的n年期内发生保险 责任范围内的死亡，保险人即刻给付保险金；如果被保 险人再生存至n年期满，保险人在第n年末支付保险金 的保险。 假定(x)投保延期m年的n年期两全保险，保额1元。 基本函数关系 0, t m 0 , t m bt t 1, t m z b v v , m t m n

保险精算-第4章1-人寿保险的精算现值

保险精算-第4章1-人寿保险的精算现值
例如， 一个26岁的人考虑用保险金支付他退休之后死亡时 的丧葬费用，于是，他投保了一份延期34年的终身 寿险。如果人在退休前死亡，他工作期间的丰厚收 入会解决其丧葬费用，如果在退休之后死亡，则保 险公司会为他的一个很体面的葬礼支付保险金。这 就是一份终身寿险，但延期了34年。
延期m年的终身寿险
定义 保险人对被保险人在投保m年后发生的保险责任 范围内的死亡均给付保险金的险种。
zt btvt vt , t 0
Z bv TT
vT
t0
Ax 表示终身寿险的趸缴纯保费。
Ax
E(Z)
z f (t)dt
0t
T
vt p dt e t p dt
0
tx
xt
0
tx
xt
方差为
Var(Z )
例2
设 (x)要投保终身寿险，保险金额1元，签单时其未
来寿命 T 的概率密度函数为
0
T
v e
1
A x:n
表示n年期死亡保险的精算现值。
方差公式：
Var(Z ) E(Z 2 ) [E(Z )]2 E(Z 2 ) (A1 )2 x: n|
E(Z 2 ) n z 2 f (t)dt 0t T
n
n
v2t f (t)dt e f 2 t (t)dt
0
T
0
T
记为
（相当于利息力翻倍以后求n年期寿险的趸缴保费）
f T
(t)
1 60
，
0
t
60
0， 其他
利息强度为 ( 0) ，在签单时的保险金给付现值随机
变量为 Z，试计算： (1) A x
(2)Var(Z )
(3)满足P(Z ) 0.9的 .

第三章___人寿保险的精算现值

第三章___人寿保险的精算现值
l 100张保单的未来赔付支出总现值
l 平均每张保单的未来赔付现值（保单的精算现 值）为：134.68元。
PPT文档演模板
第三章___人寿保险的精算现值
基本符号
l
—— 岁投保的人整值剩余寿命
l bk+1——保险金在死亡年末给付函数 l vk+1 ——贴现函数 l zk+1 ——保险赔付金在签单时的现时值
l 它的实质是在统计意义上的收支平衡。是在大数场合下，收入 期望现时值等于支出期望现时值
l 精算现值（包含两层含义）：
l 保险赔付在投保时的期望现值
l 把所有可能的赔付先折现到保单签发时刻，然后再求 期望值
l 精算现值=趸缴净保费
l 由于赔付的不确定性源于人的死亡不确定，所以， 以连续型（离散型）未来寿命为随机变量，来求期 望值。
第三章___人寿保险的精算现值
n年定期保险的趸缴净保费
给付函数 给付现值随机变量
趸缴净保费
PPT文档演模板
第三章___人寿保险的精算现值
递增终身寿险(一年递增一次）
l 给付现值随机变量
l 趸缴净保费
PPT文档演模板
第三章___人寿保险的精算现值
递增终身寿险（连续递增）
l 给付现值随机变量
l 在UDD假设下，有
l当
时，相当于连续寿险的趸缴纯保费
PPT文档演模板
第三章___人寿保险的精算现值
例3.7
l 某人在30岁时投保了50 000元30年期两全保险， 设预定利率为6%，以中国人寿业经验生命表 （1990-1993年，男女混合表），求这一保单 的趸缴净保费。
l 其他条件同上。但保单规定：投保的前10年死 亡赔付50 000元，后20年死亡赔付30 000元， 满期存活给付20 000元。求这一保单的趸缴净 保费。

保险精算课件第3章寿险精算现值

保险精算课件第3章寿险精算现值

4.2 死亡即付的人寿保险
死亡即付就是指如果被保险人在保障 期内发生保险责任范围内的死亡 ，保险公 司将在死亡事件发生之后，立刻给予保险 赔付。
死亡即刻赔付时刻是一个连续型随机 变量，它距保单生效日的时期长度就等于 被保险人签约时的剩余寿命。
1.终身寿险 对(x) 的1单位元终身寿险，死亡即付现值 随机变量为
死亡时存活的整数年数，这时的变额寿险称为 标准递增的变额寿险。
标准递增的终身寿险
Z (K 1)vK 1, K 0,1, 2,

1
…
11
…
x x+1 x+2
…

1…
1
1…
…
1
1…
1
1…
x+n-1 x+n
其精算现值以 (IA)x 表示，有

(IA)x E(Z ) (k 1)vk1k qx k 0
k 0
qx

1 lx
x 1
d xk v k 1
k 0
●赔付现值随机变量的方差：
Var(Z ) E(Z 2 ) [E(Z )]2


E(Z 2)
v2(k1) k qx
e q 2 (k 1) kx
k 0
k 0
E(Z 2) 相当于以计算趸缴净保费利息力
Ax E(Z )
0
vt

t
px

x t dt


v k 1 t
k

t
px

x t dt
k 0


v1 sk
0
sk
px
xsk ds

保险精算课件 第3章寿险精算现值

保险精算课件 第3章寿险精算现值
0 k= 0 k=
ω−x− 1
ω−x− 1
延期m年的 延期 年的n 年的 年定期寿险 延期m年的 延期 年的 终身寿险 n年期两全 年期两全 保险
A =A m
1 xn :
1 xm n : +
−A
1 xm :
1 xm :
m
A = A −A x x
1 xn :
A: = A +A xn
1 xn :
死亡年末给付趸缴纯保费公式归纳 延期m年的 延期 年的n 年的 年期两全保险
k+ 1
(x) 的1单位元 年两全保险的精算现值为 单位元n年两全保险的精算现值为 单位元
A:n =∑ ⋅ k q +v ⋅ n p v x x x
k+ 1 n k= 0
n− 1
=A +A
1 x:n
1 x: n
其中 A 精算现值。 精算现值。
1 x: n
表示1单位元给付纯生存险的 表示 单位元给付纯生存险的 单位元给付
☆两全保险现值随机变量的方差 为两全保险现值随机变量， 设Z为两全保险现值随机变量，Z1为n年 为两全保险现值随机变量 年 定期现值随机变量， 定期现值随机变量，Z2为n年纯生存保险现值 年纯生存保险现值 随机变量， 不会同时发生， 随机变量，则Z1和Z2不会同时发生，我们有
V r(Z) =V r(Z +Z ) a a 1 2 =V r(Z )+V r(Z )−2E Z )⋅ E Z ) a 1 a 2 ( 1 ( 2
1. 终身寿险
对 (x 的1单位元死亡年末赔付终身寿 ) 表示。 险，其精算现值以 A 表示。 x 记 K(x) =k 为 x岁投保人的整值剩余寿命， 下面计算 A x
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

保险精算中的人寿保险的精算现值的模型
一、人寿保险简介
保险精算学主要分为两大类：一个是所谓的人寿保险（寿险精算），另一个是非人寿保险。

前者主要以人的寿命、身体或健康为“保险标的”的保险。

非人身保险主要包括：汽车保险、屋主保险、运输保险、责任保险、信用保险、保证保险等。

而这次我们主要讨论人寿保险。

狭义的人寿保险是以被保险人在保障期是否死亡作为保险标的的一种保险。

广义的人寿保险是以被保险人的寿命作为保险标的的一种保险。

它包括以保障期内被保险人死亡为标的的狭义寿险，也包括以保障期内被保险人生存为标底的生存保险和两全保险。

人寿保险的分类
根据不同的标准，人寿保险有不同的分类：
（1）以被保险人的受益金额是否恒定进行划分，可分为：定额受益保险，变额受益保险。

（2）以保障期是否有限进行划分，可分为：定期寿险和终身寿险。

（3）以保单签约日和保障期是否同时进行划分分为：非延期保险和延期保险。

（4）以保障标的进行划分，可分为：人寿保险（狭义）、生存保险和两全保险。

人寿保险的特点
1：保障的长期性
这使得从投保到赔付期间的投资收益（利息）成为不容忽视的因素。

2：保险赔付金额和赔付时间的不确定性
人寿保险的赔付金额和赔付时间依赖于被保险人的生命状况。

被保险人的死亡时间是一个随机变量。

这就意味着保险公司的赔付额也是一个随机变量，它依赖于被保险人剩余寿命分布。

3：被保障人群的大多数性
保险公司可以依靠概率统计的原理计算出平均赔付并可预测将来的风险。

人寿保险趸缴纯保费厘定的原理
1、假定
传统的人寿保险产品的趸缴纯保费是在如下假定下厘定的：假定一：同性别、同年龄、同时参保的被保险人的剩余寿命独立同分布。

假定二：被保险人的剩
余寿命分布可以用经验生命表进行拟合。

假定三：保险公司可以预测将来的投资受益（即预定利率）。

2、原理
保险公司在上面三个假定条件下，按照净均衡的原则来厘定趸缴纯保费的数额。

而趸缴纯保费是指在保单生效日一次性支付将来保险赔付金的期望现时值。

记t ：保单生效到赔付的时间
Vt：从赔付时刻回溯至保单生效时的利息贴现，称为贴现函数。

b t：赔付时刻赔付的金额，或者说是被保险人的受益金额，称为受益函数。

Z t：受益赔付额回溯到保单生效时的现时值，称为现时随机变量，它是一个依赖于赔付时间、赔付金额和贴现函数的随机变量，简记为 Z，有 Z t=V t*b t
按照净均衡原则，趸缴纯保费就等于 E(Z t)。

人寿保险的种类
死亡保险是以被保险人的死亡为保险事故的人寿保险。

根据合同期间的不同,死亡保险可分为终身保险与定期保险。

终身保险也称为终身寿险,是并不规定死亡期限的保险。

定期保险是以约定被保险人在一定期间内死亡为给付条件的保险。

若被保险人过期不死,则保险合同终止,保险人无给付义务,也不退还已收的保险费。

生存保险也称为纯粹生存保险,是以被保险人在经历一定时期后仍继续生存为给付条件的保险。

生死合险也称为混合保险是指在一定的期间内,不论被保险人是生存还是死亡,保险人均给付保险金
二、精算现值与两种情况下的人寿保费模型
精算现值是指现值的期望值,又称期望现值。

以英文首字母缩写“APv”，记之。

假设被保险人在投保(或签单)时的年龄为x，其未来取整余寿为k。

b为k+1年末给付的保险金额，v k+1为k+1处给付1个单位在签单时的贴现因子，Z为在k+1年末支付保额在签单时(保单生效时或时刻0时)的现值。

则
因此,在离散型的人寿保险模型下,现值随机变量Z的期望值E(Z)的一般表达式为
（公式一）
对于人寿保险,现值随机变量Z的期望值E(Z)称为趸缴纯保费,即保额的精算现
值。

A:下面,我们运用公式一考察离散型寿险模型下死亡保险的保额的精算现值。

1.死亡保险
死亡保险分为n年定期保险和终身寿险。

(1)n年定期保险
假设(x)签约离散型的保险金额为1个单位的n年定期保险，有关函数为：
投保人在第k+1年内的死亡概率为，根据公式1可得：
(2)终身寿险
对于(x)投保离散型的保额为1个单位的终身寿险，保额的精算现值用A x示。

对于投保人自投保之日起,无论何时死亡,保险人均需在被保险人死亡之年的年末支付1个单位的保额。

B:连续型的人寿保险模型下死亡保险的精算现值
保险人在被保险人的未来寿命T=T(x)时给付保险金,即在被保险人死亡时立即给付。

这样的保险模型称为连续型人寿保险模型,也称死亡即刻赔付的人寿保险。

假设被保险人在投保(或签单)时的年龄为x岁,b t在t时刻支付的保额,v`称为利息贴现系数,
Z t为在t时刻支付的保额在签单时的现值。

以表示保额连续支付的各险种的精算值,则
1．死亡保险
（1）n年定期寿险
则其保额的精算现值为
（公式2）(2)终身寿险
令公式2中，得
三、关于人寿保险精算现值的计算题
某养老保险计划规定的退休给付为每年10000元。

假设职工参加养老保险计划的年龄为25岁，正常退休年龄为60岁。

已知利率为5%，采用个体成本分配精算成本法，在水平分摊成本的方式下，计算：（1）年正常成本（以参加养老保险计划的年龄为计算时点）；（2）40岁时的精算债务；（3）65岁时的精算债务。

某人在30岁投保，假设生存函数在0到100间均匀分布，z为死亡赔付现值随机变量，已知利息力为0.05，求和。

解：（1）由于生存函数在0到100间均匀分布，但x=30时，剩余寿命在[0,70]间均匀分布，概率密度f（t）=1/70，所以
四、学习的心得和感受
这门课我觉得还挺实用的，偏于应用型。

让我们初步了解保险的一些内容，保险费用的包含和不同保险的费用的不同算法，把基础打牢，了解一些保险类的原理。

而且这门课也是一个综合，和我们以前学过的不少课都是有密切的关联。

使用的就有统计学使用的方法，也有“保险统计”细分，和金融、投资关系就更密切了，保险也是一种投资，对风险的投资，是金融的一个大类，而财务会计和保险精算也是相辅相成的，为公司更好的运营，保驾护航，都可以减小公司的风险，一个是报告公司的经营状况，让公司管理层对公司状况有比较清楚的了解，从而对风险有所准备，防患于未然。

学习这门课感触挺大的，金融方面的费用是那么眼睛，且保险精算是很重要的学科，和很多行业都有关联，国家也需要多多培养这方面的人才。