误差修正模型ECM

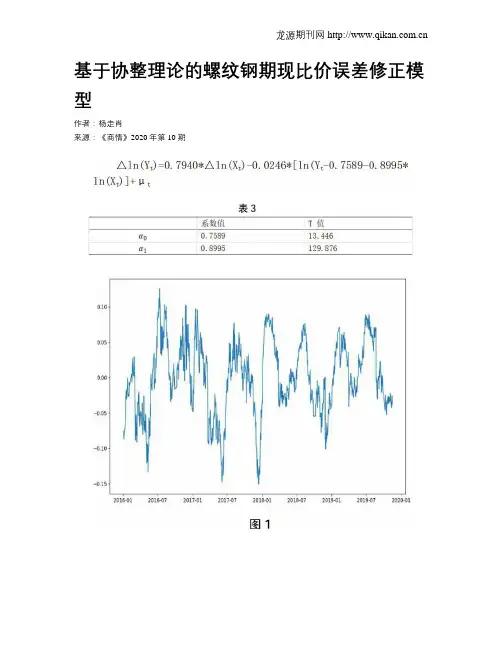
基于协整理论的螺纹钢期现比价误差修正模型作者：杨走肖来源：《商情》2020年第10期【摘要】在实体经济中，各企业受成本价格冲击越来越嚴重，国内经济政策推动实体企业和金融企业相结合，各实体企业对套期保值业务越来越重视。

实证表明期货价格和现货价格存在协整关系，期限价比存在均值回归效应，在此基础上建立误差修正模型，使套利在建仓时机的把握上更加稳健可靠，并捕捉比价难以发现的套利机会。

【关键词】现货; 期货; 均值回归; 误差修正模型一、研究背景目前，我国期货市场在不断拓展，品种不断增多，交易策略不断完善。

在实体经济中，各企业受成本价格冲击越来越严重，国内经济政策推动实体企业和金融企业相结合，各实体企业对套期保值业务越来越重视。

一定程度上，期货价格与现货价格的走势比以往更加密切，研究两者之间的关系变化对研究期现货未来价格走势都有好处。

我们通常跟踪基差（现货价格-期货价格）的变化来追踪期现价格走势的变化以及制定后续的相关套利交易策略。

本文试图检验期现价格在统计意义上的长期均衡稳定关系，并且从比价的角度研究期现价格之间的关系，两者是如何相互修正比价的。

目前在螺纹钢与焦炭跨品种套利的研究和实际操作中，螺纹钢价格与焦炭价格的比值，即：螺纹钢价格/焦炭价格（以下称作“比价”）是主要的跟踪标的。

当比价高于某一设定区间的上限时，套利者抛螺纹钢买焦炭;当比价低于某一设定区间的下限时，套利者买螺纹钢抛焦炭;当比价回落或回升至某一水平时，套利者获利离场。

一般情况下，金融价格时间序列是非平稳数据（序列的均值或自协方差随时间的推移而改变）。

若序列是非平稳的，采用直接估计的方法容易导致“伪回归”的产生（两者不存在）。

如果序列经过d阶差分后变为平稳，则称该序列是d阶单整序列;如果非平稳序列之间为同阶单整，且它们的线性组合是平稳序列，则称两者具有协整关系，即长期稳定的均衡关系。

就期货合约而言，如果两个不同品种期货合约具有协整关系，即表明两个合约价格在长期具有均衡关系。

VaR(Value at Risk)按字面解释就是“在险价值”，其含义指：在市场正常波动下，某一金融资产或证券组合的最大可能损失。

更为确切的是指，在一定概率水平（置信度）下，某一金融资产或证券组合价值在未来特定时期内的最大可能损失。

VaR的表示公式[1]用公式表示为：P(ΔPΔt≤VaR)=a字母含义如下：P——资产价值损失小于可能损失上限的概率，即英文的Probability。

ΔP——某一金融资产在一定持有期Δt的价值损失额。

VaR——给定置信水平a下的在险价值，即可能的损失上限。

a——给定的置信水平VaR从统计的意义上讲，本身是个数字，是指面临“正常”的市场波动时“处于风险状态的价值”。

即在给定的置信水平和一定的持有期限内，预期的最大损失量(可以是绝对值，也可以是相对值)。

例如，某一投资公司持有的证券组合在未来24小时内，置信度为95%，在证券市场正常波动的情况下，VaR值为520万元，其含义是指，该公司的证券组合在一天内(24小时)，由于市场价格变化而带来的最大损失超过520万元的概率为5%，平均20个交易日才可能出现一次这种情况。

或者说有95%的把握判断该投资公司在下一个交易日内的损失在520万元以内。

5%的几率反映了金融资产管理者的风险厌恶程度，可根据不同的投资者对风险的偏好程度和承受能力来确定。

VaR的计算系数由上述定义出发，要确定一个金融机构或资产组合的VaR值或建立VaR的模型，必须首先确定以下三个系数：一是持有期间的长短；二是置信区间的大小；三是观察期间。

1、持有期。

持有期△t，即确定计算在哪一段时间内的持有资产的最大损失值，也就是明确风险管理者关心资产在一天内一周内还是一个月内的风险价值。

持有期的选择应依据所持有资产的特点来确定比如对于一些流动性很强的交易头寸往往需以每日为周期计算风险收益和VaR值，如G30小组在1993年的衍生产品的实践和规则中就建议对场外OTC衍生工具以每日为周期计算其VaR，而对一些期限较长的头寸如养老基金和其他投资基金则可以以每月为周期。

面板数据、格兰杰因果关系、向量自回归和向量误差修正模型(2011-06-13 11:43:22)标签: 分类: 工作篇校园面板数据的计量方法1.什么是面板数据,面板数据,panel data,也称时间序列截面数据,time series and cross section data,或混合数据,pool data,。

面板数据是截面数据与时间序列综合起来的一种数据资源～是同时在时间和截面空间上取得的二维数据。

如:城市名:北京、上海、重庆、天津的GDP分别为10、11、9、8,单位亿元,。

这就是截面数据～在一个时间点处切开～看各个城市的不同就是截面数据。

如:2000、2001、2002、2003、2004各年的北京市GDP分别为8、9、10、11、12,单位亿元,。

这就是时间序列～选一个城市～看各个样本时间点的不同就是时间序列。

如:2000、2001、2002、2003、2004各年中国所有直辖市的GDP分别为: 北京市分别为8、9、10、11、12,上海市分别为9、10、11、12、13,天津市分别为5、6、7、8、9,重庆市分别为7、8、9、10、11,单位亿元,。

这就是面板数据。

2.面板数据的计量方法利用面板数据建立模型的好处是:,1,由于观测值的增多～可以增加估计量的抽样精度。

,2,对于固定效应模型能得到参数的一致估计量～甚至有效估计量。

,3,面板数据建模比单截面数据建模可以获得更多的动态信息。

例如1990-2000 年30 个省份的农业总产值数据。

固定在某一年份上～它是由30 个农业总产值数字组成的截面数据,固定在某一省份上～它是由11 年农业总产值数据组成的一个时间序列。

面板数据由30 个个体组成。

共有330 个观测值。

面板数据模型的选择通常有三种形式:混合估计模型、固定效应模型和随机效应模型。

这三类模型的差异主要表现在系数、截距以及随机误差的假设不同。

第一种是混合估计模型,Pooled Regression Model,。

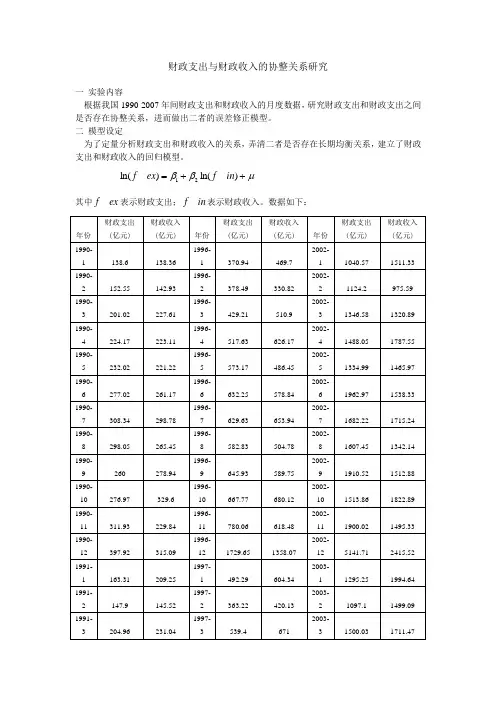
财政支出与财政收入的协整关系研究一 实验内容根据我国1990-2007年间财政支出和财政收入的月度数据，研究财政支出和财政支出之间是否存在协整关系，进而做出二者的误差修正模型。

二 模型设定为了定量分析财政支出和财政收入的关系，弄清二者是否存在长期均衡关系，建立了财政支出和财政收入的回归模型。

μββ++=)_ln()_ln(21in f ex f其中ex f _表示财政支出；in f _表示财政收入。

数据如下：数据来源：统计年鉴三、实证分析 1、数据处理由数据结构可以看出，数据存在季节波动。

首先利用X-12季节调整方法对这两个指标进行季节调整，消除季节因素，然后去对数。

2、单位根检验经济时间序列数据往往出现非平稳的情况，如果直接对数据建立回归模型，可能会出现伪回归的现象，因此在做回归之前，运用ADF 方法，对数据进行单位根检验。

对ln(ex f _)、ln(in f _)及其一阶差分进行单位根检验，具体检验结果如下所示：ln(ex f _)原值单位根检验Null Hypothesis: LNF_EX has a unit rootExogenous: ConstantLag Length: 5 (Automatic based on SIC, MAXLAG=14)t-StatisticProb.*Augmented Dickey-Fuller test statistic 0.519686 0.9871 Test critical values: 1% level -3.4614785% level -2.87512810% level -2.574090*MacKinnon (1996) one-sided p-values.f_)一阶差分单位根检验ln(exNull Hypothesis: D(LNF_EX) has a unit rootExogenous: ConstantLag Length: 4 (Automatic based on SIC, MAXLAG=14)t-Statistic Prob.* Augmented Dickey-Fuller test statistic -10.83446 0.0000 Test critical values: 1% level -3.4614785% level -2.87512810% level -2.574090*MacKinnon (1996) one-sided p-values.f_)原值单位根检验ln(inNull Hypothesis: LNF_IN has a unit rootExogenous: ConstantLag Length: 11 (Automatic based on SIC, MAXLAG=14)t-Statistic Prob.* Augmented Dickey-Fuller test statistic 0.763850 0.9932 Test critical values: 1% level -3.4624125% level -2.87553810% level -2.574309*MacKinnon (1996) one-sided p-values.f_)一阶差分单位根检验ln(inNull Hypothesis: D(LNF_IN) has a unit rootExogenous: ConstantLag Length: 10 (Automatic based on SIC, MAXLAG=14)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -8.161494 0.0000Test critical values:1% level -3.462412 5% level -2.87553810% level-2.574309*MacKinnon (1996) one-sided p-values.汇总检验结果如下表所示：财政收入和财政支出的对数的原值和一阶差分的单位根检验结果指标 ADF 值P 值ln(ex f _) 0.519686 0.9871 ln(ex f _)的一阶差分-10.83446 0.0000 ln(in f _) 0.763850 0.9932 ln(in f _)的一阶差分 -8.1614940.0000从上表中的ADF 值和P 值可以看出：当显著性水平为0.05时，对ln(ex f _)和ln(in f _)的原值进行检验时，检验结果都表明不能拒绝“存在单位根”的原假设；而当对ln(ex f _)和ln(in f _)的一阶差分进行检验时，检验结果都表明拒绝“存在单位根”的原假设。

E-G两步法协整检验和误差修正模型的建立实验内容：使用Eviews软件进行E-G两步法协整检验的操作，并建立误差修正模型。

分析我国居民实际可支配收入与居民实际消费之间是否存在长期均衡关系。

实验数据：我国的实际居民消费和实际可支配收入，变量均为剔除了价格因素的实际年度数据，样本区间为1978—2006年。

数据来源于各年的统计年鉴。

实验过程：1、实际居民消费CSP等于名义居民消费CS除于CPI，实际可支配收入INC 等于名义可支配收入YD除于CPI。

把上述数据导入到Eviews中，建立相应的系列。

2、对实际居民消费CSP序列和实际可支配收入INC序列进行ADF单位根检验，检验结果如下：注：△表示一阶差分，△2 表示二阶差分。

（C T K）表示检验类型，C表示常数项，T表示趋势项，K 表示滞后阶数。

﹡表示在1%的显著性水平下显著。

从ADF单位跟检验结果可知，csp和inc系列均为2阶单整系列，即csp~I(2)，inc~I(2)。

因此可以对csp和inc系列进行协整关系检验。

3、建立回归方程。

点击菜单栏里的quick，选择下拉菜单的estimate equation。

在出现的对话框中依次输入：CSP、C、INC。

如下图所示：4、点击确定得到方程回归结果，如下图所示：5、在方程对象框中，单击proc，选择 make residual series，生成方程的残差系列，命名为“e”。

并对e系列进行ADF单位根检验，检验结果如下图所示：检验形式为即不包含常数项也不包含趋势项。

检验结果表明，在5%的显著性水平下，e 系列是平稳系列。

所以csp和inc 存在协整关系，也就是长期均衡关系。

6、建立误差修正模型：误差修正模型（ECM：Error Correction Model）的基本形式最早是由Davidson、Hendry、Srba和Yeo在1978年提出的，因此又称之为DHSY模型。

在建立经济模型的时候，经常会需要用数据的动态非均衡过程来逼近经济理论的长期均衡过程，最一般的模型就是自回归分布滞后模型（ADL：autoregressive distributed lag）。

平稳性检验协整理论(Cointegration)是Granger和Engle在20世纪80年代中后期提出的，用于非平稳变量组成的关系式中长期均衡参数估计的技术。

在实际运用时，一般是首先对时间变量序列及其一阶差分序列的平稳性进行检验；其次是检验变量间协整关系，并建立修正误差模型(ECM)；第三对具有协整关系的时间变量序列的因果关系进一步检验分析。

协整理论从分析时间序列的非平稳性着手，探求非平稳经济变量间蕴含的长期均衡关系。

即两经济时序数据{xt，yt}在以xt为横坐标、yt为纵坐标上，其散点图围绕在某一条直线yt=β0 β1xt的周围，直线对点(xt，yt)起着引力线的作用，当(xt，yt)偏离该直线时，引力线的作用会使它们回到直线附近，虽然不能立即到达直线上，但存在着回归这条直线的总趋势。

定义如下：若变量向量置中所有分量均为d阶单整，即Xt～I(d)，且存在一个非零向量βt使得向量Zt=βXt～I(d-b)，b>0，则称变量向量Xt为具有d，b阶协整关系，表示为Xt～ CI(d，b)，而β为协整向量。

从经济学的观点看，协整可理解为经济时序变量间存在着一种均衡力量，使非平稳的不同变量在长期内一起运动，即如果变量之间存在长期稳定关系(协整关系)，变量的增长率表现共同的增长趋势。

反之，如果这两个或以上变量不是协整的，则它们之间不存在一个长期的均衡关系。

协整理论从变量之间是否具有协整关系出发选择模型的变量，使得数据基础更加稳定，统计性质更为优良。

平稳性检验方法有：DF检验法、ADF检验法、PP检验法、霍尔工具变量法、DF-GLS变量法、KPSS检验法等等。

ADF法(Augmented-Dicky-full-er)检验变量的稳定性，即进行平稳性检验，回归方程如下：并作假设检验：H0：a2=0，H1：a2≠0，如果接受假设H0而拒绝H1，则说明序列xt存在单位根，因而是非稳定的；否则说明序列xt不存在单位根，即是稳定的。

固定资产投资与经济增长的误差修正模型分析【摘要】为了研究固定资产投资对经济增长的作用方向和效果，本文以重庆市为例结合当地实际经济发展状况，运用计量经济学中的协整关系检验和格兰杰因果检验及误差修正模型，对重庆1985～2009年的国内生产总值与固定资产投资之间的相关关系进行了实证分析，得出结论与启示，固定资产投资有效地推动了重庆市经济增长，二者之间存在着长期稳定关系，但还是要警惕投资过热后的一些问题并提出了相关建议。

【关键词】gdp；固定资产投资；误差修正模型在当今经济的高速列车上，投资需求已然成为我们国家经济一直保持着平稳较快增长的重要因素。

其中投资尤以固定资产投资为主要项目，因此固定资产投资对各省的经济增长起到了主要的促进作用。

重庆作为西南地区的唯一直辖市，成为国家振兴西部经济建设的先头军，也是西部战略中的重要门户。

近年来不仅大力引进外资，同时也增加了固定资产投资的力度，增加了劳动就业，通过比较优势和后发优势逐渐缩小与东部地区之间的差异，多管齐下的促进经济的增长。

为了研究固定资产投资对重庆市经济增长的作用方向和效果，本文欲采用1985～2009年的数据进行回归分析、协整检验、误差修正模型和格兰杰因果检验等计量方法，研究重庆市固定资产对gdp的影响。

由于计算过程中的数据繁琐，所有数据处理均采用excel和eivews软件实现模型计算。

一、重庆固定资产投资与经济增长的实证分析（一）数据选取和分析本文所使用的样本取自1986-2010年重庆统计年鉴，为了剔除通货膨胀因素和消除数据产生的异方差影响，保证数据的可比性，所有数据除以当年的cpi并取对数，即lngdp、lnfai，从而增强数据的平稳性，使结论更准确真实。

同时为了大家直观了解fai对gdp 的作用以及两者的相关性，我们在样本区间对两者数据做了散点图，如图1所示。

（二）协整分析1．变量的平稳性检验。

本文采用的数据是时间序列，采用的方法是对数据进行差分检验，即adf单位根检验。

1.1 Granger和ECM模型分析方法 中国电力与经济增长关系的分析检验过程分为时间序列的平稳性检验、Granger因果关系和协整关系检验，最后建立ECM模型进行分析。 1.1.1 时间序列平稳性检验

Granger因果关系、协整关系检验、ECM模型都要求时间序列是平稳的。本检验采用的是ADF（Augmented Dickey-Fuller）和PP（Phillips-Perron）的单位

根检验与平稳性检验[88]。两个检验都是检验零假设，H0，时间序列ty是非平稳的。ADF检验是基于模型（2-1）。

titkiittuyyty11 （2-1）

其中，k是最优滞后期，由于检验结论对滞后阶数较为敏感，在实际操作的过程中视具体情况而定，一般取使赤池信息准则AIC（Akaike Information Criterion）和施瓦茨准则SC（Schwarz Criterion）值达到最小的方程中的参数k就是最优滞后阶数。若ADF检验值在一定的置信水平下大于临界值，则接受原假设，即时间序列为非平稳，若ADF检验值在一定置信水平下小于临界值，则拒绝原假设，即时间序列为平稳。 但时间序列也应考虑结构的变化等，应做结构断点分析。由Zivot和Andrews提出的考虑虚拟变量的两个模型可以用来进行结构断点分析，一个是模型A，考虑断点前后截距的变化，另一个是模型C，考虑时间断点前后截距与斜率的共同变化，参见式（2-2）与（2-3）。

模型A titkiittteyyDUty11 (2-2) 模型C titkiitttteyyDTDUty11 (2-3) 式中，α, β, θ, γ, ρ, ξ是系数；t=1，…，T 表示时间；TB 表示出现结构断点的时间；如果 t > TB，DUt=1，否则为0；如果t > TB，DTt = t - TB，否则为0。

附录：数量级（阶数）和收敛速度设 {a T }∞=1T 是一个实数列，{g T }∞=1T 是一个正实数列，则有如下定义。

1．如果 ()T T T g a ∞→lim = 0，则称a T 是g T 的低阶数量级。

记作a T = o (g T )。

2．如果存在实数M ，且对于所有的T 有 T T g a ≤ M ，则称a T 的数量级不超过g T 。

或a T 的最大数量级是g T 。

记作a T = O (g T )。

对于随机变量序列，数量级应是概率测度的数量级。

设{x T }是一个随机变量序列，{g T }∞=1T 定义如上。

则有如下定义。

3．若对于任何ε > 0，有∞→T lim p{ | x T - x | > ε } = 0，则称 {x T } 依概率收敛于随机变量x ，或x T的概率极限是x 。

记作∞→T lim p x T = x 。

4．如果∞→T lim p (T T g x )= 0，则称x T 是g T 的概率测度低阶数量级。

记作x T 是o p (g T )的。

5．若对于任何ε > 0，存在一个正实数M ε，使∞→T lim p{ |T T g x | ≥ M ε} ≤ ε，则称x T 的概率测度最大数量级不超过g T ，记作x T 是O p (g T )的。

在计量经济学的理论推导中，常用T α表示g T 。

当T →∞时，如果序列θˆ(T )/ T α →0，则定义θˆ(T )的数量级低于T α。

记为o (T α)。

如果序列θˆ(T )/ T α 是有界的，则定义θˆ(T )的最大数量级为T α。

记为O (T α)。

例，对于数列∑=Tt t 1= (1 + 2 + 3 + 4 … + T ) = (1/2)T (T + 1)当T →∞时，因为21T t T t ∑=→1/2, 所以∑=Tt t 1是O (T 2)的。

同理∑=Tt t 12= (1/6)T (T +1) (2T +1) 是O (T 3)的。

向量误差修正一 模型的概述1 VEC 模型向量误差修正模型VEC 是协整与误差修正模型的结合。

只要变量之间存在协整关系，就可以由自回归分布滞后模型导出误差修正模型，即VEC 模型是建立在协整基础上的V AR 模型，主要应用于具有协整关系的非平稳时间序列建模。

V AR 模型的表达式为：11=1=+++ =1, 2,, p t t i t i t t i t T ---∆∆∑y ecm y x αΓH ε式中t y 为k 维内生变量列向量，其各分量都是非平稳的()1I 变量；t x 是d 维外生向量，代表趋势项、常数项等确定性项；每个方程都是一个误差修正模型，1t -ecm 是误差修正项向量，反映变量之间的长期均衡关系；系数矩阵α反映了变量之间偏离长期均衡状态时，将其调整到均衡状态的调整速度；解释变量的差分项的系数反映各变量的短期波动对作为被解释变量的短期变化的影响；t ε是k 维扰动向量。

2 诊断检验2.1 Johansen 协整检验Johansen 协整检验基于回归系数进行检验，其基本思想为： 对()VAR p 模型11=1=+++ =1, 2,, p t t i t i t t i t T ---∆∆∑y ecm y x αΓH ε两端减去1t -y 再变形可以得到11=1=+++ =1, 2,, p t t i t i t t i t T ---∆∆∑y y y x ∏ΓH ε其中的,t ∆y t j -∆y ()=1,2,j p 都变为()0I 变量构成的向量，只要1t -∏y 是()0I 的向量，即1t -y 的各分量之间具有协整关系，就能保证t ∆y 是平稳过程，而这主要依赖于矩阵∏的秩。

设∏的秩为r ，则0<<r k 时才有r 个协整组合，其余k r -个关系仍为()1I 关系。

这种情况下，∏可以分解为两个k r ⨯阶矩阵α和β的乘积：=∏αβ'其中()()=,=r r r r αβ，则模型变为1'1=1=+++ =1, 2, , p t t i t i t t i t T ---∆∆∑y y y x αβΓH ε式中'1t -βy 为一个()0I 向量，β为协整向量矩阵，其每一列所表示的1t -y 的各分量线性组合都是一种协整形式，矩阵β决定了1t -y 的各分量之间协整向量的个数（r ）与形式。

第1篇摘要本实验旨在探究协整关系的存在及其特征，通过构建经济时间序列模型，分析变量之间的长期稳定关系。

实验选取了国内生产总值（GDP）、消费者价格指数（CPI）和货币供应量（M2）作为研究对象，运用协整理论和误差修正模型（ECM）进行实证分析。

实验结果表明，GDP、CPI和M2之间存在长期的协整关系，且短期波动可以通过ECM得到有效修正。

关键词协整关系；误差修正模型；GDP；CPI；M21. 引言协整关系是指两个或多个非平稳时间序列在某种线性组合下成为平稳的。

协整理论在经济学、金融学等领域有着广泛的应用，有助于揭示变量之间的长期稳定关系。

本实验通过对GDP、CPI和M2三个变量的协整关系进行探究，旨在为相关领域的研究提供理论支持和实证依据。

2. 实验方法本实验采用以下方法：（1）数据来源：选取我国2000年至2020年的季度数据，数据来源于国家统计局。

（2）模型构建：对GDP、CPI和M2进行单位根检验，确定其平稳性；接着进行协整检验，构建协整方程；最后，利用误差修正模型（ECM）分析短期波动。

（3）软件工具：使用EViews软件进行数据处理和模型构建。

3. 实验步骤（1）数据预处理：对原始数据进行对数化处理，以消除时间序列中的异方差性。

（2）单位根检验：采用ADF（Augmented Dickey-Fuller）检验方法，对GDP、CPI 和M2进行单位根检验。

（3）协整检验：采用Engle-Granger两步法进行协整检验，确定变量之间是否存在长期稳定关系。

（4）协整方程构建：根据协整检验结果，构建协整方程，分析变量之间的长期稳定关系。

（5）误差修正模型（ECM）构建：根据协整方程，构建ECM模型，分析短期波动。

4. 实验结果与分析（1）单位根检验结果：经ADF检验，GDP、CPI和M2的原始序列均为非平稳序列，其一阶差分序列为平稳序列。

（2）协整检验结果：经Engle-Granger两步法检验，GDP、CPI和M2之间存在长期的协整关系。

常用的协整检验方法协整检验是一种用于检测时间序列数据之间是否存在长期关系的统计方法。

在金融经济学中，协整检验被广泛应用于价格和收益率之间的关系分析，以及股票市场和货币市场之间的关系研究。

以下是一些常用的协整检验方法：1. 奥格尔检验（Engle-Granger Test）：奥格尔检验是最常见的协整检验方法之一。

它基于两个时间序列的单位根检验结果，通过构建误差修正模型（Error Correction Model，ECM）来检验它们之间的协整关系。

该方法的优点是简单易用，但对数据的要求较高，仅适用于两个时间序列的情况。

2. 约翰逊检验（Johansen Test）：约翰逊检验是一种多元协整检验方法，可以同时检验多个时间序列之间的协整关系。

它基于向量自回归模型（Vector Autoregression Model，VAR）和特征根检验，通过判断特征根的数量和位置来确定协整关系的存在与否。

约翰逊检验适用于具有多个时间序列的复杂情况，但计算复杂度较高。

3. 格兰杰因果检验（Granger Causality Test）：格兰杰因果检验是一种常用的时间序列分析方法，用于检验两个时间序列之间的因果关系。

如果两个时间序列之间存在协整关系，那么它们之间可能存在因果关系。

格兰杰因果检验通过引入滞后项来模拟时间序列之间的动态关系，并通过F统计量检验滞后项的显著性来判断因果关系的存在与否。

4. 面板数据协整检验（Panel Cointegration Test）：面板数据协整检验是用于面板数据（Panel Data）的协整检验方法。

面板数据包含多个个体（Cross-section）和多个时间点（Time-series），可以用来分析不同时间点和不同个体之间的协整关系。

常用的面板数据协整检验方法包括西姆斯-休斯特（Seemingly Unrelated Regression，SUR）和极限法（Pedroni）等。

协整检验方法的选择应根据具体的研究目的和数据特点来确定。