井中蜗牛-数学故事

蜗牛爬井的数学题
【原创版】
目录
1.蜗牛爬井的问题描述
2.蜗牛爬井问题的数学解法
3.蜗牛爬井问题的实际应用
正文
1.蜗牛爬井的问题描述
蜗牛爬井是一个有趣的数学问题。

假设有一只蜗牛要从井底爬到井口，它每天可以向上爬 1 米，然后又滑下 0.5 米。

蜗牛在第一天爬 1 米，第二天爬 0.5 米，第三天爬 0.5 米，第四天爬 1 米，依此类推。

在第几天，蜗牛能够爬出井口？
2.蜗牛爬井问题的数学解法
为了解决这个问题，我们可以使用一个简单的数学公式。

假设蜗牛需要爬 n 米才能到达井口，那么蜗牛在第 n-1 天能够爬到 (n-1) 米高的位置。

在第 n 天，蜗牛再爬 1 米，就能够达到井口。

因此，蜗牛在第 n 天能够爬出井口。

具体到蜗牛爬井问题，我们可以得出结论：蜗牛在第 4 天能够爬出
井口。

因为蜗牛在第一天爬 1 米，第二天爬 0.5 米，第三天爬 0.5 米，第四天爬 1 米，所以在第四天，蜗牛总共爬了 2.5 米，刚好能够爬出井口。

3.蜗牛爬井问题的实际应用
蜗牛爬井问题看似简单，但它实际上反映了一个重要的数学原理，即等差数列求和公式。

这个公式可以应用于各种实际问题，例如计算一个项目的总进度、预测一个物种的数量增长等。

通过掌握这个公式，我们可以
更好地理解和解决实际问题。

蜗牛爬井问题也是一个有趣的思维训练题，它可以帮助我们培养数学思维和逻辑推理能力。

在解决这个问题的过程中，我们需要仔细分析问题，找出问题的关键信息，然后运用数学知识来解决问题。

教学目标：1、使学生理解蜗牛爬井的数学意义2、通过本课练习与讲解，掌握蜗牛爬井计算的几种技巧，会灵活运用，并能解决实际问题重、难点：掌握并熟练蜗牛爬井的数学意义解综合题型授课内容：课题：“蜗牛爬井”问题◆◆【知识梳理】故事导入：一只蜗牛不小心掉进了一口枯井里。

它趴在井底哭了起来。

一只癞蛤蟆爬过来，瓮声瓮气的对蜗牛说：“别哭了，小兄弟！哭也没用，这井壁太高了，掉到这里就只能在这生活了。

我已经在这里过了多年了，很久没有看到过太阳，就更别提想吃天鹅肉了！”蜗牛望着又老又丑的癞蛤蟆，心里想：“井外的世界多美呀，我决不能像它那样生活在又黑又冷的井底里！”蜗牛对癞蛤蟆说：“癞大叔，我不能生活在这里，我一定要爬上去！请问这口井有多深？”“哈哈哈……，真是笑话！这井有１０米深，你小小的年纪，又背负着这么重的壳，怎么能爬上去呢？”“我不怕苦、不怕累，每天爬一段，总能爬出去！”第二天，蜗牛吃得饱饱的，喝足了水，就开始顺着井壁往上爬了。

它不停的爬呀，到了傍晚终于爬了５米。

蜗牛特别高兴，心想：“照这样的速度，明天傍晚我就能爬上去。

”想着想着，它不知不觉地睡着了。

早上，蜗牛被一阵呼噜声吵醒了。

一看原来是癞大叔还在睡觉。

它心里一惊：“我怎么离井底这么近？”原来，蜗牛睡着以后从井壁上滑下来４米。

蜗牛叹了一口气，咬紧牙又开始往上爬。

到了傍晚又往上爬了５米，可是晚上蜗牛又滑下４米。

爬呀爬，最后坚强地蜗牛终于爬上了井台。

小朋友你能猜出来，蜗牛需要用几天时间就能爬上井台吗？◆◆【融知于题】◆◆【典型例题分析】例题1：从前井里住着一只蜗牛，它很想到井外去看看。

可是井有13米，它白天向上爬2米，可是到了夜里，不知不觉就下滑1米，照这样计算：蜗牛从井底出来需要几天。

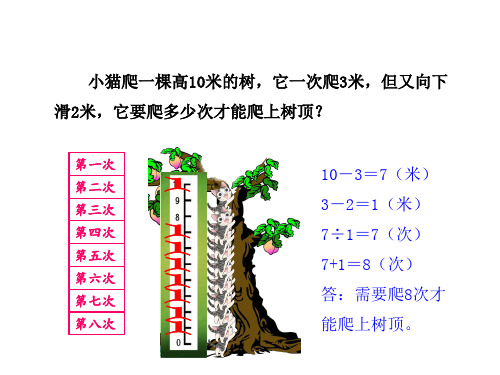
练习：小猫练习爬树，每次爬上去3米又下滑1米，照这样，小猫几天能爬上5米高的树。

例题2：可是井有20米，它白天向上爬5米，可是到了夜里，不知不觉就下滑3米，照这样计算：蜗牛从井底出来需要几天。

第一讲蜗牛爬井（上）“蜗牛爬井”是一类非常有趣的数学问题,做这类题目要仔细,会比较,会分段思考,并善于整理不同阶段的变化情况.在考虑“蜗牛爬井”问题的时候注意两点：1、第一次爬上去,第二次滑下来,实际上是爬上去多少？2、最后一次爬上去之后就不会再滑下来了.本讲内容用到简单乘除法,需要引导学员背诵乘法口诀.1、理解“蜗牛爬井”的特点；2、初步感知分段解决问题的数学思想；3、通过蜗牛爬井这个有趣的故事,激发学生学习的兴趣.一只蜗牛不小心掉进了一口10米深的枯井里,白天沿着井壁往上爬了5米,晚上睡着以后又从井壁上滑下来4米,第二天蜗牛咬紧牙又往上爬了5米,可是,晚上蜗牛又滑下4米,如此反复,爬呀爬,最后,坚强的蜗牛终于爬上了井台.小朋友,你能猜出来,蜗牛用了几天时间才爬上井台吗？【解析】井深10米,蜗牛每天爬5米,滑下4米,实际蜗牛每天爬1米,照这样计算：第一天蜗牛爬到了1米处,第二天爬到了2米处,第三天爬到了3米处,第四天爬到了4米处,第五天爬到了5米处,第六天再爬5米后就爬上井台了.所以蜗牛用了6天的时间.有一只蜗牛从井底沿着井壁向上爬,每天白天向上90厘米,但是晚上又向下滑落60厘米.井高6米,蜗牛多少天才能爬出井？【解析】6米＝600厘米,蜗牛每天白天向上爬90,晚上下落60,相当于一天向上爬30厘米. 因为最后爬上井口的那个白天不再向下滑落,所以我们可以先算出蜗牛几天可以向上爬（600－90）＝510厘米,然后再加上一天就可以了.（90-60）×17=510（厘米）,17+1＝18（天）,正好爬上井口,不再向下滑落,所以18天爬上井口.讲演者：得分：讲演者：得分：一只蜗牛从井底向上爬,每天清晨到傍晚向上爬5米,夜间又滑下来2米,第6天天黑前爬到井口,问井最深可能是多少米？【解析】前5天爬了（5-2）×5=15（米）,最后一白天最多爬5米,所以井最深15+5=20（米）.蜗牛在10米深的井底往上爬,每天清晨到傍晚向上爬5米,夜间又滑下若干米,第6天天黑前爬到井口,问每天夜间下滑多少米？【解析】1天可以向上爬（10-5）÷（6-1）=1（米）,每天夜间下滑5-1=4（米）.蜗牛爬竿,竿长20厘米,从某天清晨开始,每个白天可以向上爬10厘米,晚上又要下滑4厘米,白天到黑夜总是如此.那么蜗牛在第几个白天才爬到竿的顶上？【解析】估算：2天可以爬（10-4）×2=12（厘米）,剩下20-12=8（厘米）,一天即可爬到顶,所以第3天到达杆顶.小海龟在回大海的路上遇到一座沙丘,上坡路长20米,小海龟白天只能向上爬10米,晚上还要滑下9米,小海龟不怕饥饿,经过几天的奋斗终于爬到沙丘顶,然后从下坡路一下滑到了海边.那么从小海龟第一个白天爬的早晨算起,第几个白天爬到沙丘顶？【解析】（20-10）÷（10-9）=10（个）全天,最后一天爬10米,10+1=11（个）白天.一位跳舞的人沿一条直线,前进4步,后退2步,这条直线的两头相距50步.那么,从这头舞到另一头,他一共跳了多少步？【解析】（50-4）÷（4-2）=23（组）进退,最后一次前进4步,一共跳了（4+2）×23+4=142（步）井深11米,井底有一只青蛙.一日早晨开始,青蛙要爬出井口到大地上来,每过1小时可以上爬3米,接着的1小时又滑下1米,如此上下.青蛙必须爬出井口,并离开井口一步,才不会再滑入井中.那么青蛙在第几个小时才安全？【解析】（3-1）×4=8（米）,剩下11-8=3（米）,1小时可以爬到井口,还没有离开井口,又开始下滑了,紧接着的1小时又会下滑1米,再过1小时,可以爬出井口,并离开井口一步,不会再滑入井中,一共需要2×4+1+1+1=11（小时）.一只青蛙从井底向上爬,白天上爬4米,晚上下滑3米,第5天爬到井口,问井最深可能是多少米？【解析】前4天爬了（4-3）×4=4（米）,最后一白天最多爬4米,所以井最深4+4=8（米）.蜗牛爬竿,竿子长10米,从某天清晨开始,每个白天可以向上爬6米,晚上却要下滑若干米, 第3天刚好爬上竿顶,蜗牛每天晚上下滑多少米？【解析】1天可以向上爬（10-6）÷（3-1）=2（米）,每天夜间下滑6-2=4（米）.一位跳舞的人沿一条直线,前进4步,后退2步,这条直线的两头相距20步.那么,从这头舞到另一头,他一共跳了多少步？【解析】（20-4）÷（4-2）=8（组）进退,最后一次前进4步,一共跳了（4+2）×8+4=52（步）.以“差透了的家庭作业”为题讲一个故事,注意：1、故事的完整性；2、细节的观察与描述；3、语言表达的清晰和流畅性.这种训练,对数学审题和逻辑思维能力的培养非常有效.。

小学趣味数学之蜗牛爬井教学目标：1、使学生理解蜗牛爬井的数学意义2、通过本课练习与讲解，掌握蜗牛爬井计算的几种技巧，会灵活运用，并能解决实际问题重、难点：掌握并熟练蜗牛爬井的数学意义解综合题型授课内容：课题：“蜗牛爬井”问题◆◆【知识梳理】故事导入：一只蜗牛不小心掉进了一口枯井里。

它趴在井底哭了起来。

一只癞蛤蟆爬过来，瓮声瓮气的对蜗牛说：“别哭了，小兄弟！哭也没用，这井壁太高了，掉到这里就只能在这生活了。

我已经在这里过了多年了，很久没有看到过太阳，就更别提想吃天鹅肉了！”蜗牛望着又老又丑的癞蛤蟆，心里想：“井外的世界多美呀，我决不能像它那样生活在又黑又冷的井底里！”蜗牛对癞蛤蟆说：“癞大叔，我不能生活在这里，我一定要爬上去！请问这口井有多深？”“哈哈哈……，真是笑话！这井有１０米深，你小小的年纪，又背负着这么重的壳，怎么能爬上去呢？”“我不怕苦、不怕累，每天爬一段，总能爬出去！”第二天，蜗牛吃得饱饱的，喝足了水，就开始顺着井壁往上爬了。

它不停的爬呀，到了傍晚终于爬了５米。

蜗牛特别高兴，心想：“照这样的速度，明天傍晚我就能爬上去。

”想着想着，它不知不觉地睡着了。

早上，蜗牛被一阵呼噜声吵醒了。

一看原来是癞大叔还在睡觉。

它心里一惊：“我怎么离井底这么近？”原来，蜗牛睡着以后从井壁上滑下来４米。

蜗牛叹了一口气，咬紧牙又开始往上爬。

到了傍晚又往上爬了５米，可是晚上蜗牛又滑下４米。

爬呀爬，最后坚强地蜗牛终于爬上了井台。

小朋友你能猜出来，蜗牛需要用几天时间就能爬上井台吗？◆◆【融知于题】◆◆【典型例题分析】例题1：从前井里住着一只蜗牛，它很想到井外去看看。

可是井有13米，它白天向上爬2米，可是到了夜里，不知不觉就下滑1米，照这样计算：蜗牛从井底出来需要几天。

练习：小猫练习爬树，每次爬上去3米又下滑1米，照这样，小猫几天能爬上5米高的树。

例题2：可是井有20米，它白天向上爬5米，可是到了夜里，不知不觉就下滑3米，照这样计算：蜗牛从井底出来需要几天。

蜗牛爬井公式好嘞，以下是为您生成的文章：咱们在数学的世界里，经常会碰到各种各样有趣又有点“烧脑”的问题。

今天咱们就来聊聊那个听起来有点特别的“蜗牛爬井公式”。

话说有一天，我带着小侄子去公园散步。

这小家伙呀，一路上蹦蹦跳跳，对啥都好奇。

走着走着，我们来到了一个小池塘边，看到一只蜗牛正在努力地往池塘边的石头上爬。

小侄子一下子来了精神，蹲在那儿眼睛一眨不眨地盯着蜗牛看。

我就趁机问他：“宝贝，你说这蜗牛要是从井底往上爬，白天爬 3 米，晚上下滑 2 米，那井深 10 米，它几天能爬上来呀？”小侄子歪着脑袋想了半天，一脸迷茫地看着我。

其实呀，这就是一个典型的蜗牛爬井问题，而解决它的关键就是咱们要说的蜗牛爬井公式。

咱们来假设蜗牛每天向上爬的距离是 a 米，每天晚上下滑的距离是b 米，井深为 h 米。

那么蜗牛爬上来需要的天数就是：（h - a）÷（a - b）+ 1 。

就拿刚刚说的那个例子，蜗牛白天爬 3 米，也就是 a = 3；晚上下滑2 米，b = 2；井深 10 米，h = 10 。

咱们套进公式里算算，（10 - 3）÷（3 - 2） + 1 = 8（天）。

这公式看起来好像有点复杂，其实理解起来并不难。

你想啊，蜗牛每天实际上向上爬的距离就是白天爬的减去晚上滑的，也就是 a - b 。

那它在最后一天白天爬 a 米到达井口之前，剩下的距离就是 h - a 米。

用剩下的距离除以每天实际向上爬的距离，就是除去最后一天之前爬的天数，再加上最后一天，就是总共需要的天数啦。

再给您举个例子，假如井深 15 米，蜗牛白天爬 4 米，晚上下滑 1 米。

咱们算算，a = 4，b = 1，h = 15 ，代入公式就是（15 - 4）÷（4 - 1）+ 1 = 4（天）。

这个蜗牛爬井公式在咱们生活中也能找到类似的情况呢。

比如说减肥，你每天努力运动消耗一些卡路里，但是又忍不住吃了点零食摄入一些卡路里，这就像蜗牛爬井，每天有进有出。

➢ “蜗牛爬井”问题的特点； ➢ 求所花时间；求进退情况。

➢ 学习通过画图及逆推的方法来解答“蜗牛爬井”类问题； ➢ 培养学生对实际问题的分析能力；➢ 激发学生用数学思维解决实际问题的兴趣。

➢ 逆推法及画图分析法。

➢ 掌握“蜗牛爬井”问题的分析技巧。

➢ 教师：玩偶； ➢ 学生：玩偶。

第 42 讲 蜗牛爬井一只蜗牛不小心掉进了一口枯井里。

它趴在井底哭了起来。

一只癞蛤蟆爬过来，瓮声瓮气的对蜗牛说：“别哭了，小兄弟！哭也没用，这井壁太高了，掉到这里就只能在这生活了。

我已经在这里过了多年了，很久没有看到过太阳，就更别提想吃天鹅肉了！”蜗牛望着又老又丑的癞蛤蟆，心里想：“井外的世界多美呀，我决不能像它那样生活在又黑又冷的井底里！”蜗牛从10米深的井底往上爬，每天从清晨到傍晚向上爬5米，夜间又滑下来4米，像这样从某天清晨开始，第几天能爬到井口呢？【flash 】1. 动画：蜗牛掉井里——蛤蟆对话 2. 井深10米，（井边标注10格）蜗牛每天从清晨到傍晚向上爬5米，夜间又滑下来4米。

（用计数器记录天数）点击画面显示问题：像这样从某天清晨开始，第几天能爬到井口呢？3. 如题:动画呈现蜗牛爬井的情况。

4. 第6天时，点击画面，向上爬5米，无需下滑到达井口。

➢ 解决以图代数的关键是什么？答： 仔细观察图片的变化规律或共同点，注意分析数字间及数与图之间的区别与联系。

➢ 结合问题，从题目中你能获得哪些信息？ ➢ 蜗牛实际每天向上爬几米？分析力计算力 语言力【分析】图示蜗牛爬井问题，教学生利用线段图分析此类问题。

1. 最后一天爬5米就上井台了，不再滑下来。

之前路程为：10米-5米=5米2. 每天爬5米，下滑4米，也就是每天只爬了1米，则之前用了5天。

3. 总共5+1=6（天）【解答】如题所述，这只蜗牛需要6天能爬出井。

原来要爬出井也不是这么困难的事情啊！蜗牛开始假想另外一种情况：若从井底往上爬，每天从清晨到傍晚向上爬6米，夜间又滑下来4米，第4天爬到井口，井深多少米？【分析】每天爬6米，下滑4米，实际每天爬6—4=2（米）。

蜗牛爬井的数学题
摘要：
1.蜗牛爬井的问题描述
2.蜗牛爬井的数学模型
3.蜗牛爬井问题的解决方法
4.蜗牛爬井问题的实际应用
正文：
1.蜗牛爬井的问题描述
蜗牛爬井是一个经典的数学问题，描述的是一只蜗牛从井底往上爬，每次只能爬1 米，然后休息1 天。

蜗牛在爬到井口之前，总共需要爬多少米？休息多少天？
2.蜗牛爬井的数学模型
我们可以通过一个简单的数学模型来描述蜗牛爬井的问题。

假设井深为h 米，蜗牛每天爬1 米，那么蜗牛需要爬h 米才能到达井口。

由于每天爬1 米后需要休息1 天，所以蜗牛需要爬h/1 = h 天，休息h-1 天。

3.蜗牛爬井问题的解决方法
为了解决蜗牛爬井问题，我们可以使用一个简单的循环。

首先，初始化一个变量h 为井深，然后使用一个while 循环，每次让蜗牛爬1 米，判断蜗牛是否到达井口。

如果到达井口，则输出蜗牛总共爬了多少米，休息了多少天。

如果没有到达井口，则继续循环。

4.蜗牛爬井问题的实际应用
蜗牛爬井问题看似简单，实际上在生活中有很多应用。

比如，我们可以通过这个模型来描述一个人在规定时间内完成一个任务的过程。

假设任务总量为T，每天完成1 个单位，那么这个人需要多少天才能完成任务？。

蜗牛爬井的数学题
蜗牛爬井的数学题是一个经典的思维问题。

问题描述如下：
假设有一口深度为h的井，蜗牛每天白天往上爬m米，晚上
休息时下滑n米。

蜗牛爬井的进程是怎样的？
解答：
蜗牛每天都会往上爬m米，晚上则下滑n米。

所以，每天蜗
牛实际上是爬了m-n米。

第一天蜗牛会爬上m米，然后晚上下滑n米，所以蜗牛在第
一天结束后实际上爬了m-n米。

第二天蜗牛会再次爬上m米，然后晚上下滑n米，所以蜗牛
在第二天结束后实际上爬了2*(m-n)米。

依次类推，第三天蜗牛爬了3*(m-n)米，第四天爬了4*(m-n)
米 ......。

可以发现，蜗牛每过一天，实际上爬的高度都是(m-n)的倍数。

现在我们需要找到蜗牛第一次爬出井口（到达或超过h米）的时间。

假设蜗牛第一次爬出井口时共爬了x天，那么有：
x*(m-n) >= h
整理得：
x >= h / (m-n)
所以蜗牛第一次爬出井口的时间是h除以(m-n)的结果（向上取整）。

可以进一步分析得出：如果m <= n，则蜗牛无法爬出井口。

如果m > n，则蜗牛肯定可以爬出井口。

这道题可以帮助锻炼孩子的思维能力和数学推理能力，同时也是一个实际生活中的有趣问题。