200671380521_常用弹塑性材料模型

第五章 弹塑性模型理论5.1 概述弹塑性理论可以分为两种，塑性增量理论和塑性全量理论。

塑性增量理论又称塑性流动理论，塑性全量理论又称塑性形变理论。

在塑性增量理论中，将物体在弹塑性变形阶段的应变ij ε分为两部分：弹性应变e ij ε和塑性应变p ij ε。

塑性应变增量ij d ε的表达式为e p ij ij ij d d d εεε=+ (5.1.1)式中，弹性应变增量d e ij ε可以用广义虎克定律计算，塑性应变增量d p ij ε可以根据塑性增量理论计算。

塑性增量理论主要包括三部分：（1） 屈服面理论；（2） 流动规则理论；（3） 加工硬化（或软化）理论。

在塑性形变理论中是按全量来分析问题的。

它在盈利状态和相应的应变状态之间建立一一对应的关系。

塑性形变理论实质上是把弹塑性变形过程看成是非线性弹性变形过程。

严格说，在弹塑性变形理论的应用是有条件的。

严格讲，只有在等比例加载条件下，应用塑性变形理论可以得到精确解。

所谓等比例加载是指在加载过程中，各应力分量是按同一比例增加的。

严格的等比例加载是很难满足的，在土工问题中可以说是不可能的。

在简单加载条件下应用塑性形变理论分析有时也可以取得较好效果。

近些年来建立的土体弹塑性模型大部分是根据塑性增量理论建立的。

本章主要介绍塑性增量理论，在最后一节简要介绍塑性形变理论。

5.2 屈服面得概念首先讨论理想弹塑性材料。

理想弹塑性材料受力到什么程度才开始发生塑性变形呢？在简单拉伸时，问题是很明显的。

当应力等于屈服应力σs 时，塑性变形开始产生。

σs 值是可以在拉伸试验应力-应变曲线上找到的。

然而在复杂应力状态时，问题就不是这样简单了。

一点的应力状态由六个应力分量确定。

在复杂应力状态下，显然不能任意选取某一个应力分量的数值作为判断材料是否进入塑性状态的标准。

因此需要在应力空间或应变空间来考虑这一问题。

在土塑性力学中，常用的应力空间有三维主应力空间、p 、q （或σm ，σ1-σ3）应力平面、以及132σσ+，132σσ-应力平面等。

１ 钢 丝 帘 线 材 料 模 型 基 本 原 理
旦 一 Ａ — Ａ 一 ／ ｏ ｏ
一
（ ）
ｎ （ １＋ 十 ｎ ｅ ｎ ） （ ５ ）
真实 塑性 应变 （ ￡ 。 ） 可 以 由真 实 总 应 变 （ ｅ ） 和
及杨 氏模 量 （ Ｅ） 得 到
ｅ 一 ｅｔ一
关 系［ 引。
而 钢丝 帘线 又是子 午线 轮胎结 构 中的 主要受 力材 料； 因此 ， 对其 进行 受力 分析 已经成 为现 代轮 胎结 构 设计 和分 析 的重要工 作之 一 。 由于轮 胎结 构及
其材 料 的复 杂性 ， 至今 还 没有 有 效 的试 验 手段 来 直观、 定 量地 分析 轮胎 内部材 料 的受力 变形 情况 。 随 着计 算机 和数 学 、 力 学等 自然科 学 的发展 ， 有 限
采用试 验 与 Ａｂ ａ ｑ ｕ ｓ软 件 模 拟 相 结 合 的 方 式， 在 充分 考虑 材料 非线 性 、 多股 加捻钢 丝之 间复 杂 接触 和拉 伸后 截面变 化 的情况 下 ， 较直观 、 简 便
地 获得 了钢 丝帘线 弹 塑性材 料模 型参 数 。结果 表
关键词 ： 钢丝帘线； 有 限 元分 析 ； 材 料 模 型
中 图分 类 号 ： Ｔ Ｑ３ ３ ｏ ． ３ ８ ９
文献 标 志 码 ： Ｂ
文章编号： １ ０ ０ ６ — ８ １ ７ １ （ ２ ０ １ ４ ） １ ０ — ０ ６ ０ ２ — ０ ３
众所 周 知 ， 轮胎 是汽 车安 全 的关键 部件 之一 ，
考虑 塑性 变 形 的不 可 压 缩 性 ， 并 假 设 弹 性 变
形 也是 不可压 缩 的 ， 建 立真 实应 力 （ ） 与 名 义应 力

一、05Cr17Ni4Cu4Nb弹性、塑性仿真参数及应用
1.材料简介
05Cr17Ni4Cu4Nb即17-4PH，属马氏体不锈钢。

2.弹性、塑性仿真参数
MAT PLASTIC KINEMATIC模型参数：σ0=1076Mpa，E=186.8Gpa，Ep=1705Mpa，C=21999S-1，P=1.632。

3.材料应用
沉淀硬化型不锈钢，常用在高强度冲击结构，耐腐蚀性与304相当。

适用于400℃以下的高强度耐蚀件，例如，飞机、导弹的紧固件，涡轮发动机安装边和阀门等。

二、022Cr17Ni12Mo2弹性、塑性仿真参数及应用
1.材料简介
022Cr17Ni12Mo2即316L，属奥氏体不锈钢。

2.弹性、塑性仿真参数
弹性模量E=2.1E11pa，泊松比v=0.33；Johnson-Cook模型参数A=280MPa，B=1250Mpa，n=0.76，C=0.070，m=0.82，Tm=1800K，Tr=198K。

3.材料应用
主要做耐点蚀材料，常用于海水或其他其他介质，广泛应用于医疗器械行业。

也可用做耐热材料。

这两个选项中的所有数据点必须升序排列
Copyright © 2012 Altair Engineering, Inc. Proprietary and Confidential. All rights reserved.
NLSTAT MATS1 – 硬化准则
• HR-参数
• • • • 1 = isotropic hardening 2 = kinematic hardening 3 = mixed hardening (30% kinematic 和 70% isotropic hardening) 0<HR<1 = mixed hardening (HR*100% kinematic 和 (1-HR)*100% isotropic hardening)
V RBE3单元用于施加载荷
操作：
• 单元属性
材料：
理想的塑钢
• 材料定义
• 边界条件和载荷 • 输出请求 • 工况
Young‘s modulus: 210,000 N/mm² Poisson‘s ratio: 0.3 Yield stress: 230 N/mm²
σ
σy
E
查看：
• Out文件/收敛过程 • 应力 • 塑性应变
Copyright © 2012 Altair Engineering, Inc. Proprietary and Confidential. All rights reserved.
NLSTAT Ex.3.1: 建模 – 梁
模型：
V 3D网格
文件：beam_bending_blank.fem 600N
Copyright © 2012 Altair Engineering, Inc. Proprietary and Confidential. All rights reserved.

例题1：边长为 a 的正方形薄板，一边固支、两边简支，自由边中点A受集 中载荷 P 作用，板的塑性极限弯矩为： Mp ，求塑性极限载荷。 D
b
b
C
a
h
E A B
解：设A点的挠度为d
ABC与ACD的相对转角为q :
a
q
d
AC
cota cot b 5
j d
a
d
2 AC
j
d
ACD与CD的相对转角为j:
dr
梁计算模型
板 x o r
q(r) r
o x
m
Mx Qx
m
q(x) 极限条件：
2rMr 2rQr 2Mq
2rq(r) Mmax Mp
若梁和圆板的边界条 件在形式上相同，可 通过求解变量转换后 梁的问题得到圆板的 解答。
四、 梁模型计算圆板和环板的塑性极限载荷的步骤
1. 结构转换 o
r
o
解：
o
z
r
r a
a
z
2rM r 2rM p r r 2rq 2 3
m= 2Mp
qr 2 Mr M p 6
Mr
r a
qa2 M p M p M p 6
ql 12
Mp a2
简支圆板：
Mr
r a
0
ql 6
Mp a2
例题2：半径为 a 的简支环板，内半径为 b ，受均布载荷 q 作用，圆板单 位塑性极限弯矩为： Mp ，求塑性极限载荷。 2rq q
i 1
ai bi
( n 2) 2n 2 n
Pl M P cota i cot b i

06
结论与展望
结论
1
本文通过理论分析和有限元模拟，深入研究了弹 塑性力学基础与有限元分析在接触分析中的应用。
2
研究结果表明，弹塑性力学基础与有限元分析在 接触分析中具有较高的精度和可靠性，能够有效 地模拟复杂接触问题。
3
本文所采用的有限元分析方法在处理接触问题时 具有较好的通用性和扩展性，为进一步研究复杂 接触问题提供了有力支持。
弹塑性本构模型
弹塑性本构模型的定义
弹塑性本构模型是描述弹塑性材料力学行为的数学模型，它通过应力应变关系来描述材料的弹塑性行 为。
常见的弹塑性本构模型
常见的弹塑性本构模型包括Mohr-Coulomb模型、Drucker-Prager模型、Cam-Clay模型等。这些模 型在描述材料的弹塑性行为方面各有特点，适用于不同的材料和工程问题。
接触面完全贴合，无相对运动。
滑动状态
接触面部分贴合，存在相对运动。
混合状态
接触面同时存在分离、粘结和滑动。
接触检测与跟踪
初始接触检测
确定初始状态下接触面的位置和状态。
接触状态跟踪
实时监测接触面的运动状态和相互作用。
接触面更新
根据接触状态调整接触面的几何形状和参数。
接触刚度与阻尼
1 2
接触刚度
描述接触面间的相互作用力与相对位移的关系。
求解阶段主要进行有限元 方程的求解，得到各节点 的位移和应力等结果。
ABCD
前处理阶段主要完成有限元 模型的建立和网格划分，为 求解阶段提供输入数据。
后处理阶段主要对求解结果进 行可视化、分析和评估，为工 程设计和优化提供依据。
04
接触分析原理
接触状态描述
分离状态

常用材料弹性模量和剪切模量常用材料的弹性模量和剪切模量指的是材料在受力时的弹性性质，即材料在受力后发生形变后能够恢复到原来形状的程度。

弹性模量和剪切模量是用来描述材料的弹性行为的参数，对于材料的力学性质和设计有着重要的意义。

弹性模量（Young's Modulus）通常以E表示，是描述材料拉伸或压缩时的弹性变形性能的参数。

它的定义是材料应力和应变之间的比值，即E = σ/ε，其中σ是材料的应力，ε是材料的应变。

弹性模量的单位是帕斯卡(Pascal)，常用的单位还包括千帕斯卡(Kilopascal)和兆帕斯卡(Megapascal)等。

弹性模量越大，表示材料的抵抗变形的能力越强。

常见材料的弹性模量差别很大，以下是一些常用材料的弹性模量的范围：-铁:100-220GPa-钢:200-210GPa-铝:70-80GPa-铜:100-150GPa-橡胶:0.01-0.1GPa-塑料:1-5GPa-木材:10-20GPa剪切模量（Shear Modulus）通常以G表示，是描述材料在剪切应力作用下发生剪切变形时的弹性变形性能的参数。

剪切应力指的是一种在材料中形成剪切力的应力，剪切变形是指材料在受到剪切力时产生的形变。

剪切模量定义为剪切应力和剪切应变之间的比值，即G = τ/γ，其中τ是剪切应力，γ是剪切应变。

剪切模量的单位也是帕斯卡(Pascal)。

常见材料的剪切模量范围如下所示：-钢:70-85GPa-铝:25-30GPa-铜:40-50GPa-橡胶:0.001-0.1GPa-塑料:1-5GPa-木材:1-5GPa弹性模量和剪切模量之间存在一定的关系，通过杨氏模量和剪切模量可以计算出材料的泊松比（Poisson's Ratio）。

泊松比（Poisson's Ratio）通常以ν表示，是描述材料杨氏模量和剪切模量之间关系的参数。

泊松比定义为材料横向应变和纵向应变之间的比值，即ν = - ε_t/ε_l，其中ε_t是材料的横向（剪切）应变，ε_l是材料的纵向（拉伸或压缩）应变。

弹性模量:一般地讲，对弹性体施加一个外界作用力，弹性体会发生形状的改变（称为“形变”），“弹性模量”的一般定义是：单向应力状态下应力除以该方向的应变。

材料在弹性变形阶段，其应力和应变成正比例关系（即符合胡克定律），其比例系数称为弹性模量。

弹性模量的单位是达因每平方厘米。

“弹性模量”是描述物质弹性的一个物理量，是一个统称，表示方法可以是“杨氏模量”、“体积模量”等。

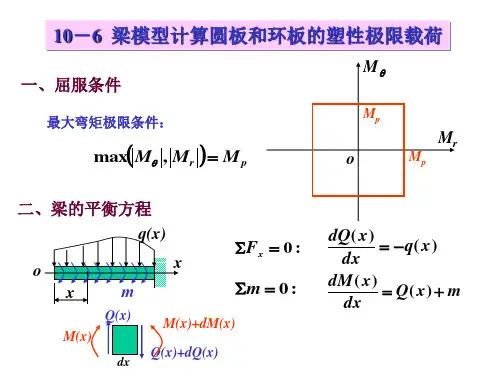
常用材料弹性模量:1 镍铬钢、合金钢206 79.38 0.25～0.32 碳钢196～206 79 0.24～0.283 铸钢172～202 - 0.34 球墨铸铁140～154 73～76 -5 灰铸铁、白口铸铁113～157 44 0.23～0.276 冷拔纯铜127 48 -7 轧制磷青铜113 41 0.32～0.358 轧制纯铜108 39 0.31～0.349 轧制锰青铜108 39 0.3510 铸铝青铜103 41 -11 冷拔黄铜89～97 34～36 0.32～0.4212 轧制锌82 31 0.2713 硬铝合金70 26 -14 轧制铝68 25～26 0.32～0.3615 铅17 7 0.4216 玻璃55 22 0.2517 混凝土14～23 4.9～15.7 0.1～0.1818 纵纹木材9.8～12 0.5 -19 横纹木材0.5～0.98 0.44～0.64 -20 橡胶0.00784 - 0.4721 电木1.96～2.94 0.69～2.06 0.35～0.3822 尼龙28.3 10.1 0.423 可锻铸铁152 - -24 拔制铝线69 - -25 大理石55 - -26 花岗石48 - -27 石灰石41 - -28 尼龙1010 1.07 - -29 夹布酚醛塑料4～8.8 - -30 石棉酚醛塑料1.3 - -31 高压聚乙烯0.15～0.25 - -32 低压聚乙烯0.49～0.78 - -33 聚丙烯1.32～1.42 - -。

DYNAFORM材料参数说明DYNAFORM材料参数说明18#材料模型：（幂指数塑性材料模型）没有考虑材料的厚向异性，只在一些简单的各向同性材料中应用。

MASS DENSITY——质量密度；YOUNG MODULUS——杨氏模量；POISSONS RATIO——泊松比；STRENGTH COEFF（K）——强度系数；HARDENING EXPONENT（N）——强化系数，也就是人们常说的硬化指数；STRAIN RATE PARAM （C）——Couper—symonds应变率系数C；STRAIN RATE PARAM （P）——Couper—symonds应变率系数P；INITIAL YIELD STRESS——初始屈服应力；FORMULATION——用公式表示。

24#材料模型：（分段线性材料模型）主要用于一些各向同性材料的冲压分析中。

MASS DENSITY——质量密度；YOUNG MODULUS——杨氏模量；POISSONS RATIO——泊松比；YIELD STRESS——屈服应力；TANGENT MODULUS——切变模量；FAILURE PL。

STRAIN——材料失效时的等效塑性应变；STEP SIZE FOR EL. DEL——段数；STRAIN RATE PARAM （C）——Couper—symonds应变率系数C；STRAIN RATE PARAM （P）——Couper—symonds应变率系数P；36#材料模型（Barlat’s-3 Parameter Plasticity Model）——3参数Barlat材料模型这种材料模型适用于任何薄板金属成形分析，特别是对象铝合金必须用次模型分析。

使用此模型一般输入以下参数：MASS DENSITY（质量密度）；YOUNG MODULUS（杨氏模量）；POISSONS RATIO（泊松比）；EXPONENT FACE M（Barlat指数m）；LANKFORD PARAM R0（各向异性参数r0）；LANKFORD PARAM R45（各向异性参数r45）；LANKFORD PARAM R90（各向异性参数r90）；HARDENING RULE（EXPON．）（硬化规律：对于线性硬化模型，HR=1；对于幂指数硬化模型，HR=3；对于分段线性硬化模型，不需要输入HR）；ＭATEIAL PARAM P1（K）和ＭATEIAL PARAM P2（N）是材料参数：⑴对于线性硬化模型：P1=切线模量=tg(α); P2=屈服应力σs；⑵对于幂指数硬化模型：P1=k（强化系数）；P2=n（强化指数）；⑶对于分段线性硬化模型，不需要输入：HR，P1，P2，E0，SPI 等参数的值。

O.71×106 O.84×106 O.17×106 O.56×106 （0.196～O.146）×106 （O.214～O.164）×106 （O.232～O.182）×106 （O.1～O.12）×106 （O.005～O.01）×106 80 （O.02～O.03）×10
6
2.7×105 3.2×105 O.7×105 2.2×105 O.27 O.42 O.25 O.1～O.18 O.1～O.18
6
一览表
状态
退 火 或高 温 回 火 退 火 或高 温 回 火 退 火 或高 温 回 火 淬火 热轧/退火 退 火 或高 温 回 火 退 火 或高 温 回 火 退 火 或高 温 回 火 退 火 或高 温 回 火 退火
硬度（HB）
≤156 ≤179 ≤156 ≤187 ≤197 ≤192 ≤229/≤207 ≤229 ≤229 217～321 241览表
名 称 弹性模量E kgf/cm2 （1.15～1.60）×106 （1.43～1.57）×106 （2.0～2.1）×106 2.1×106 1.1×106 1.3×106 1.15×10
6
弹剪模量G kgf/cm2 4.5×105 （7.45×7.76）×105 8.1×105 8.1×105 4.O×105 4.9×105 4.2×10
5
泊松比μ O.23～O.27
灰铸铁白口铸 铁 球墨铸铁 碳钢 镍铬钢、合金 钢 轧制纯铜 冷拔纯铜 轧制磷青铜 冷拔黄铜 轧制锰青铜 轧制铝 铸铝青铜
O.24～O.28 O.25～O.30 O.31～O.34
0.32～O.35 O.32～O.42 0.35 O.32～O.36
（0.91～O.99）×106 1.1×106 O.69×10

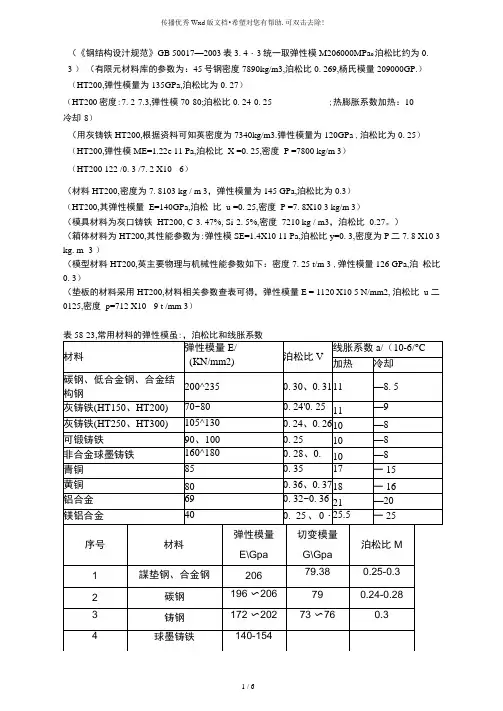
（《钢结构设汁规范》GB 50017—2003表3. 4・3统一取弹性模M206000MPa o泊松比约为0.3 ）（有限元材料库的参数为：45号钢密度7890kg/m3,泊松比0. 269,杨氏模量209000GP.）（HT200,弹性模量为135GPa,泊松比为0. 27）（HT200密度:7. 2-7.3,弹性模70-80;泊松比0. 24-0. 25 ;热膨胀系数加热：10冷却-8）（用灰铸铁HT200,根据资料可知英密度为7340kg/m3.弹性模量为120GPa ,泊松比为0. 25）（HT200,弹性模ME=1.22e 11 Pa,泊松比X =0. 25,密度P =7800 kg/m 3）（HT200 122 /0. 3 /7. 2 X10 - 6）（材料HT200,密度为7. 8103 kg / m 3，弹性模量为145 GPa,泊松比为0.3）（HT200,其弹性模量E=140GPa,泊松比u =0. 25,密度P =7. 8X10 3 kg/m 3）（模具材料为灰口铸铁HT200, C-3. 47%, Si-2. 5%,密度7210 kg / m3，泊松比0.27。

）（箱体材料为HT200,其性能参数为:弹性模SE=1.4X10 11 Pa,泊松比y=0. 3,密度为P二7. 8 X10 3 kg. m -3 ）（模型材料HT200,英主要物理与机械性能参数如下：密度7. 25 t/m 3 ,弹性模量126 GPa,泊松比0. 3）（垫板的材料采用HT200,材料相关参数查表可得，弹性模量E = 1120 X10 5 N/mm2, 泊松比u 二0125,密度p=712 X10 - 9 t /mm 3）1 / 6名称弹性模量E切变模量G泊松比uGPa GPa謀珞钢206 79. 38 0. 25-0. 30合金钢206 79. 38 0. 25-0. 30碳钢196-206 79 0. 24-0. 28铸钢172-202 0. 3球墨铸铁140-154 73-76 0. 23-0. 27 灰铸铁113-157 44 0. 23-0.27 白口铸铁113-157 44 0. 23-0. 27冷拔纯铜127 48轧制磷青铜113 41 0. 32-0. 35轧制纯铜108 39 0. 31-0. 34轧制犠青铜108 39 0. 35铸铝青铜103 41冷拔黄铜89-97 34-36 0. 32-0. 42 轧制锌82 31 0. 27硬铝合金70 26轧制铝68 25-26 0. 32-0. 36铅17 7 0. 42玻璃55 22 0. 25混凝土14-23 4. 9-15. 7 0. 1-0. 18纵纹木材9. 8-12 0. 5横纹木材0. 5-0. 98 0. 44-0. 64橡胶0. 00784 0. 47电木 1. 96-2. 94 0. 69-2. 06 0. 35-0. 38尼龙28. 3 10. 1 0. 4可锻铸铁152拔制铝线69大理石55 花岗石48石灰石41 尼龙1010 10.7夹布酚醛塑料4-8. 8石棉酚醛塑料1・3 高压聚乙烯0. 15-0. 25低压聚乙烯0. 49-0.78聚丙烯1. 32-1.42精心整理，希望对您有所帮助!。

多孔沥青混合料粘弹塑性损伤模型易军艳;SHEN Shihui;MUHUNTHAN Balasingam;冯德成【摘要】为合理描述多孔沥青混合料在中低温度外界荷载作用下的力学特性,基于增量型本构方程,采用Weibull损伤函数、广义Maxwell粘弹模型与D-P塑性模型,构建了粘弹塑性损伤模型.以此模型为分析手段,对不同温度和加载速率下的单轴压缩应力-应交曲线进行拟合,并分析温度与加载速率对模型参数的影响规律.分析结果表明:多孔沥青混合料粘弹参数随着温度的降低逐步退化成弹性参数,塑性模型中的体积模量和剪切模量也随温度呈现出明显的粘弹特性,塑性应变产生时对应的应变值与损伤应变阙值基本保持一致,温度及加载速率对于混合料的损伤扩展也有显著影响.构建的理论模型可以有效表征多孔沥青混合料在常温和低温下受荷时的力学损伤特性.【期刊名称】《哈尔滨工业大学学报》【年(卷),期】2014(046)002【总页数】6页(P66-71)【关键词】道路工程;多孔沥青混合料;粘弹性;塑性;损伤【作者】易军艳;SHEN Shihui;MUHUNTHAN Balasingam;冯德成【作者单位】哈尔滨工业大学交通科学与工程学院,150090哈尔滨;华盛顿州立大学土木与环境工程学院,99164美国华盛顿州;华盛顿州立大学土木与环境工程学院,99164美国华盛顿州;哈尔滨工业大学交通科学与工程学院,150090哈尔滨【正文语种】中文【中图分类】U416.2由于抗滑、降噪、雨天行驶安全等优点，多孔沥青混合料愈来愈得到国内外道路工作者的重视［1-3］.但是，由于空隙较大，容易堵塞，且由于结构组成与常规密级配沥青混合料不同，强度仅靠内摩阻力与相对更弱的粘聚力提供，耐久性问题一直是制约多孔沥青混合料进一步应用的瓶颈，尤其在季节性冰冻地区使用规模更小［4-8］.多孔沥青混合料是一种典型的粘弹性材料，在常温下受荷后沥青或胶浆可以通过松弛作用消散掉部分应力.但当温度降低时，沥青类材料逐步开始显示出弹脆性，一旦破坏就会导致严重的结构松散［9-10］.鉴于多孔沥青混合料的以上特点，在季冻区应用时首先需要明确其力学特性与损伤机制.目前对材料的损伤机理研究可通过宏微观分析试验手段得到，如图像处理、工业 CT扫描技术等［11-12］.此外，理论模型也可用于损伤特性分析［13-14］.但是，以往的模型分析大多试验温度为中高温，对于多孔沥青混合料在较低温度下的损伤特点，国内外研究仍较少涉及.由此，本文基于粘弹塑性损伤模型，对多孔沥青混合料在季节性冰冻地区最不利季节的温度作用下力学行为进行分析，以期更好地理解其破坏特性，为进一步的应用提供参考.在构建本构方程之前，作如下假设:1)假设多孔沥青混合料初始损伤为0;2)多孔沥青混合料的损伤主轴与应力主轴和应变主轴重合.沥青混合料在成型后内部结构即存在不同程度的缺陷与裂纹，尽管这些缺陷与裂纹在混合料内部是离散分布的，但在连续损伤力学中，材料的这些缺陷可使用连续的内部损伤场变量表示.在岩土及路面领域的研究中，Weibull分布函数被一些学者用以描述材料内部的损伤过程，其表达式［13-14］为其中:m，n为模型参数，γ为损伤时应变门槛值.假设损伤因子D变化率满足Weibull分布，即dD/dε=φ(ε)，则损伤因子可写为在本文中，引入损伤力学中的有效应力概念，即其中为有效应力张量，σij为Cauchy应力张量.在后面的分析中，相关的应力应变都将写成有效应力或有效应变的形式，以更真实地描述损伤的演化.国内外一般使用简单的机械模型组合来描述沥青混合料的粘弹特性，如 Burgers、Kelvin、Maxwell和广义Maxwell模型等.本文对多孔沥青混合料进行单轴压缩试验，采用的是位移控制模式，即保持应变速率不变，探讨应力随时间与应变的变化情况.已有研究表明，广义Maxwell模型适用于描述恒应变率加载下的材料粘弹性为.为简化模型参数，选择2个Maxwell模型与1个弹簧并联，模型如图1所示. 该模型的连续方程可使用积分形式表示［15］为式中:t1、t2为松弛时间，t1=λ1/E1，t2=λ2/E2;˙ε为应变率;G 为松弛模量，MPa;E0、E1、E2为弹性模量分量;λ1、λ2为粘度分量.积分型本构方程当进行数据拟合时，需对其离散化，即构建增量型本构方程，因此改写式(4)为其中:σ2为由λ1、E1组成的 Maxwell模型应力，σ3为由λ2、E2组成的Maxwell模型应力，σ为模型整体应力.在选择塑性模型时，现有常用的屈服函数包括 Tresca、Von Mises、Mohr-Coulomb 与 Drucker-Prager屈服准则等.其中Tresca屈服函数即为最大剪应力理论，其函数曲线存在尖角，不利于数值计算，这也是Mohr-Coulomb屈服函数的问题.因此最终屈服函数选择应用广泛的Drucker-Prager模型，该模型屈服函数在π平面的投影为光滑连续的圆形，且考虑了静水压力的影响.其屈服函数形式为［16］其中:I1为第一主应力张量不变量，J2为第二偏应力张量不变量，k为各向同性硬化参数为累计塑性应变，a为模型参数.在屈服面上，df=0，即上式可写为在选取塑性流动规则时，已有研究表明沥青混合料的力学行为符合非关联流动法则［17-19］，即塑性势函数g并不等于屈服函数f.为了得到非关联塑性模型，Drucker-Prager塑性势函数采用与屈服函数类似的结构形式，仅将其中的参数a变为参数 b，有因此，流动法则可表示为式中:H为硬化模量，dλ为正比例标量，δij为克罗内克符号，Cijkl为弹性常数张量.如前所述，为了更好地验证模型，引入有效应力与有效应变的概念.对于本文的验证试验，加载模式为单轴压缩.因此有效应力¯σe可表示为而有效塑性应变可用增量形式表达为塑性模量定义为，且单轴方向h为其中:G为剪切模量，MPa;K为体积弹性模量，MPa.由此可求得塑性应变增量，并将总应变增量表示为试验用集料为玄武岩，其粗集料技术指标为:针片状含量10.1%，小于0.075 mm的颗粒的质量分数为 0.3%，压碎值 10.0%，粘附性等级为4级.沥青为橡胶沥青，其25℃针入度为62.3(0.1 mm)，软化点θR＆B 为63.6 ℃，RTFOT 后残留针入度比为61.1%，180 ℃粘度为2.31 Pa·s，25℃弹性恢复86.3. 试验多孔沥青混合料参考公路行业规范推荐级配范围，经过对比体积指标与性能要求确定级配［20］.其关键筛孔通过率如下:16 mm筛孔通过率为95%，4.75 mm 筛孔通过率为 20%，2.36 mm筛孔通过率为15%，0.075 mm筛孔通过率为4%.沥青用量为5.2%.试验用多孔沥青混合料试样高度与直径均为100 mm，采用旋转压实仪直接成型，空隙率控制在18%±1%.加载采用单轴压缩模式，试验温度分别为-10、0、10、20 ℃，在每种温度下施加不同应变率荷载，直至试样完全破坏.具体加载速率如下:-10 ℃下为 2、1、0.5 mm/min;0 ℃下为 5、2、1 mm/min;10 ℃下为12.5、5、2 mm/min;20 ℃下为 50、5、2 mm/min.试验过程中采集荷载与位移，并转化为应力与应变.每种试验条件下制备4或5个平行试样，在加载之前，对试样施加小应力预压.试验系统为MTS810型电液伺服试验设备.在模型中，一共有12个模型参数需要确定，即损伤模型中的m、n、γ，粘弹性模型中的 E0、E1、E2、λ1、λ2，塑性模型中的K、G、a、b.由于粘弹性模型中松弛时间t1=λ1/E1，因此粘弹性模型中的5个参数选用E0、E1、E2、t1、t2.参数的确定过程包括首先根据经验对其拟定初始值，然后采用最小平方法进行非线性拟合，拟合工具采用Excel中规划求解功能，设置迭代次数与允许误差，控制模型拟合与试验结果误差平方和最小，以确定模型参数.图2为不同温度下2 mm/min(0.000 3/s)加载速率时的试验结果与模型拟合.可以看到对于不同温度时的应力应变曲线，模型可很好地进行模拟.图3、4分别为20℃与-10℃时的试验结果与模型拟合.由于篇幅所限，本文并没有给出10℃与0℃下的试验数据.但从4种温度下的试验数据与模型拟合结果看，模型在0℃以上与试验数据拟合较好，当温度下降到-10℃时，由于沥青混合料将显示出更多的弹性，其力学性能对加载速率的依赖性减弱.因此，图4中，无论是试验结果还是模型拟合，多孔沥青混合料的加载应力应变曲线都受加载速率影响较小. 由图2～4可知当温度较高或加载速率不大时，模型拟合情况较好，但是模型在描述多孔沥青混合料在低温下力学行为的有效性方面还需进一步分析.模型参数的取值和变化是影响模型精度的重要因素.参数的变化意味着混合料某些力学特性的改变，对于判断材料属性的变化规律有较大的帮助.在前文的粘弹性模型中，假设在固定温度下的粘弹属性不变，加载速率的影响可以通过模型反映.最终得到温度与各项参数之间的关系如图5所示.可以看到随着温度的降低，E0、E1、E2、t1与t2都有不同程度的上升.但其中E1和E2当温度降低到0℃以下时变化趋势减弱，表明粘弹性模型中粘弹构件作用降低，材料开始显示出更多的弹性属性，也因此弹性模量尽管有所波动，但维持在同一水平.t1与t2表征了材料松弛应力的能力，时间越短，表明材料具有更好松弛特性，也显示出更明显的粘弹特征.因此总的来看，材料参数的变化表明:温度的下降使多孔沥青混合料由粘弹性材料向弹性材料转化，材料应力松弛能力减弱.在塑性模型中，经典弹塑性理论假设剪切模量G和体积弹性模量K为常量，不随温度或加载速率的变化而改变.但是对于多孔沥青混合料这种典型的粘弹性材料，其模量也应具有温度或频率敏感性.图6、7分别为G与K在温度与加载速率变化时的取值.尽管试验结果为离散的数据点，但通过数据回归可以绘出其变化规律. 粘弹性材料的一个重要特征就是时温等效性，即温度变化导致的性能改变也可以通过改变加载时间(或加载频率)得到.同时，粘弹性材料的力学特性(动态模量等)随温度或频率的变化呈“S”形状，即在固定温度下存在一个敏感频率范围，在这个范围内材料属性变化明显，当频率过低或过高时，材料属性随频率变化的幅度减小.从图6、7可以看到，多孔沥青混合料的剪切模量G和体积弹性模量K随温度或加载速率呈明显的S型变化，证明了模型中G和K取值的合理性.损伤模型中的γ为损伤时应变门槛值，即当应变大于γ时，认为损伤开始发展.对于受荷变形的线粘弹性材料，一般认为只要时间足够长其力学特性就可以恢复.在塑性模型中，每一应变增量后，通过屈服函数判断是否出现塑性变形，并以此作为塑性应变产生.本文认为塑性应变的出现即意味着损伤的开始，而在初始线粘弹性阶段，损伤等于0.为了验证这个假设，对塑性应变产生时对应的总应变与损伤时应变门槛值γ进行分析，结果，见图8.可以看到两者之间有着很好的线性关系，图中数据点包括不同温度与不同加载速率下的结果，但是总的趋势依然满足所作的假设.对于典型的粘弹性材料，温度和加载速率的不同，将使材料呈现出不同的损伤行为.低温和高加载速率下材料显示出弹脆性，而高温和低加载速率下材料更倾向于粘塑性.对上述不同温度及加载速率下多孔沥青混合料的损伤特性进行分析，结果如图9、10所示.为更好地比较温度的影响，图中仅给出20℃与-10℃下的曲线.可以看到，当温度为20℃时，0.000 33/s(即2 mm/min)的加载速率下多孔沥青混合料显示出更多的粘弹性，在这种情况下损伤从一开始加载就出现并缓慢增长，直到混合料不再能抵抗外荷载.而当加载速率增大时，混合料逐渐显示出明显的弹脆性，即在一定弹性范围内变形可以恢复，损伤为0，但是一旦超过这个弹性范围，损伤迅速发展，混合料很快出现脆性开裂破坏.对于-10℃时的损伤曲线，由于温度较低，沥青混合料更趋向于显示出弹性，此时混合料特性受加载速率的影响相对要小很多，因此，在不同加载速率下，损伤曲线基本相同.对于弹脆性材料，直观上看，材料越硬(即温度越低，加载速率越大)，相对应的损伤起始时间就越大，并且损伤扩展的速率也越快.图11为4种温度时0.00033/s(即2 mm/min)加载速率下混合料的损伤曲线，即单纯考虑温度对损伤特性的影响.由于本文假设塑性变形的出现即为损伤的初始，因此温度越低，出现塑性变形的时间将越长，导致初始损伤发生时的应变也越大.此外，温度的高低直接决定了损伤的扩展速率.低温下的弹脆特性将带来较快的损伤速率，而温度较高时，材料的损失扩展行为更为缓慢.1)不同温度与加载速率下多孔沥青混合料的应力-应变曲线显示出明显的粘弹效应.在高温与低应变率下，多孔沥青混合料呈现出粘弹塑性破坏;而当温度较低或应变率高时，其表现为弹脆性破坏.2)构建的粘弹塑性损伤模型可以有效反映多孔沥青混合料在较低温度下的力学行为.3)由理论模型参数随温度及加载速率的变化规律可知，随着温度的降低，多孔沥青混合料模量逐步增加，但是到一定值后升高幅度降低，同时材料应力松弛能力减弱.4)随着温度及加载速率的变化，多孔沥青混合料剪切模量和体积弹性模量也呈现出“S”型变化.损伤曲线的变化规律也证明了构建理论模型的合理性.冯德成(1968—)，男，教授，博士生导师.【相关文献】［1］ALVAREZ A E，MARTIN A E，ESTAKHRI C K，et al.Synthesis of current practice on the design，construction，and maintenance of porous friction course［R］.Texas:Texas Transportation Institute and The Texas A＆M University System，2006.［2］曹东伟，刘清泉，唐国奇.排水沥青路面［M］.北京:人民交通出版社，2010.［3］MUNDEN H J，PIERCE L M，MAHONEY J P，et al.Low noise pavement evaluation in Washington State［C］//TRB Annual Meeting.Washington:Transportation Research Board，2008:1-14.［4］POULIKAKOS L，TAKAHASHI S，PARTL M.A comparison of Swiss and Japanese porous asphalt through various mechanical tests［C］//3rd Swiss Transport Research Conference.Monte Verità/Ascona:Swiss Transport Research，2004:1-12.［5］Danish Road Institute.Noise reducing pavements-state of the art in Denmark ［R］.Denmark:Road Directorate，Ministry of Transport-Denmark，2005.［6］YILDIRIM Y，DOSSEY T，FULTS K，et al.Cold weather performance of new generation open graded friction courses［R］.Texas:Center for Transportation Research，The University of Texas at Austin，2007.［7］诸永宁.排水性沥青路面排水性能研究与排水设施的设计［D］.南京:东南大学，2004.［8］SCHAUS L，TIGHE S，UZAROWSKI L.Porous asphalt pavement designs:Canadian climate use［C］//TRB Annual Meeting.Washington:Transportation Research Board，2008:1-21.［9］MOHAN S.Winter damage of porous asphal-case study using a meso-mechanics based tool for lifetime optimization of PA［D］.Netherland:Delft University of Technology，2010.［10］LEBENS M.Porous asphalt pavement performance in cold regions［R］.Minnesota:Minnesota Department of Transportation Research Services，2009. ［11］WANG L B，FROST J D，VOYIADJIS G Z，et al.Quantification of damage parameters using X-ray tomography images［J］.Mechanics of Materials，2003，35(8):777-790.［12］肖源杰，倪富健，蒯海东，等.基于图像的粗集料形态对沥青面层抗剪性能的影响［J］.郑州大学学报:工学版，2006，27(4):44-48.［13］郑健龙，吕松涛，田小革.基于蠕变试验的沥青粘弹性损伤特性［J］.工程力学，2008，25(2):193-196.［14］邵腊庚，周晓青，李宇峙，等.基于直接拉伸试验的沥青混合料粘弹性损伤特性研究［J］.土木工程学报，2005，38(4):125-128.［15］易军艳.基于界面行为的多孔沥青混合料冻融损伤特性研究［D］.哈尔滨:哈尔滨工业大学，2012.［16］CHEN W F，HAN D J.Plasticity for structural engineers［M］.FL Fort Lauderdale:J Ross Publishing Inc，2007.［17］DARABI M K，ABU A R K，MASAD E A，et al.A thermo-viscoelastic-viscoplastic-viscodamage constitutive model for asphaltic materials［J］.International Journal of Solids and Structures，2011，48(1):191-207.［18］FLOREA D.Nonassociated elastic/viscoplastic model for bituminous concrete ［J］.International Journal of Engineering Science，1994，32(1):87-93.［19］CHEHAB G.Characterization of asphalt concrete in tension using a viscoelastoplastic model［D］.North Carolina:North Carolina State University，2002.［20］JTG F40—2004.公路沥青路面施工技术规范［S］.北京:中华人民共和国交通部，2004.。

动力弹塑性分析之纤维模型截面纤维模型采用纤维束描述钢筋或混凝土材料，通过平截面假定建立构件截面的弯矩－曲率、轴力－轴向变形与相应的纤维束应力－应变之间的关系。

截面纤维模型与以往的杆系模型相比有以下特点：1)采用混凝土和钢筋的单轴应力－应变本构关系直接计算构件的刚度，构件的恢复力特性为截面上纤维本构关系的积分结果，从而适用于任意截面特性的构件，如钢筋混凝土圆柱、型钢混凝土构件等；2) 可采用受横向约束的混凝土单轴应力－应变本构关系，以考虑横向约束作用对构件恢复力特性的影响，如钢板或纤维布抗震加固钢筋混凝土柱等；3) 在截面纤维模型的基本公式中，构件轴力与弯矩为同一截面上所有纤维内力的积分。

因此，纤维模型能直接反映构件轴力与弯矩之间的相互作用。

1 纤维模型的原理为表达方便，以平面问题为例加以说明，如图1所示，截面上距离重心轴x 处的纤维应变()x ε可以用截面重心位置的轴向应变0ε和截面的曲率φ表达为：0()s x B εεφ⎧⎫=⎨⎬⎩⎭， [1]s B x =其增量表达式为0()s x B εεφ⎧⎫=⎨⎬⎩⎭如果截面的钢筋和混凝土的应力－应变本构关系如图1d 所示为已知，则对应于应变增量的应力增量可以通过切线刚度按式（3）求得：0()()s x E x B εσφ⎧⎫=⎨⎬⎩⎭图1 截面纤维模型示意图截面上所有由纤维束的应力增量所引起的截面轴力的变化和弯矩的变化可由积分求得，最终截面的轴向应变和曲率的增量可用下式求得：01s N K M εφ−⎧⎫⎧⎫=⎨⎬⎨⎬⎩⎭⎩⎭构件杆端力和变形的关系，通过推导可得（在此不赘述）：1T A M s M A M A B B B P P B K B dz M F M M M δθθ−⎧⎫⎧⎫⎧⎫⎪⎪⎪⎪⎪⎪==⎨⎬⎨⎬⎨⎬⎪⎪⎪⎪⎪⎪⎩⎭⎩⎭⎩⎭∫ 上式即为构件杆端力与杆端变形的关系，M F 为构件的瞬时柔度矩阵，M F 的逆矩阵则为其瞬时刚度矩阵。

M F 可以通过假定构件沿杆长方向的柔度分布积分得到，也可以在构件内设置内部积分点，通过积分点的截面柔度矩阵1s K −直接积分得到。

1. 弹塑性分析中的主要问题ABAQUS 提供了多种材料的本构关系和失效准则模型弹塑性变形行为：Abaqus 默认的采用屈服面来定义各项同性屈服金属材料的弹塑性行为：σε-曲线：（四个阶段） 弹性阶段：p σσ≤，应力应变服从胡克定律：E σε=p e σσσ≤≤，σε-不再是线性关系，卸载后变形完全消失，仍属于弹性变形 屈服阶段：屈服阶段表现为显著的塑性变形，此阶段应力基本不变，应变不断增加，屈服现象的出现于最大切应力有关系，屈服极限为s σ强化阶段：材料恢复抵抗变形的能力，使它继续变形必须增加拉力，强度极限为b σ 局部变形阶段：b σσ≥后，在试样的某一局部范围内，横向尺寸突然急剧减小，形成缩颈现象卸载定律，冷作硬化（比例极限得到提高，退火后可消除）伸长率5%δ≤，称为脆性材料；5%δ≥，称为塑性材料强度极限b σ是衡量脆性材料的唯一指标，脆性材料主要用作受压杆件，破坏处发生在与轴线成45︒的斜截面上，而塑性材料主要用作受拉杆件。

应以应力和名义应变：（以变形前的界面尺寸为基础）0nom F A σ= nom o l l ε∆=真实应力和真实应变与名义量的关系：(1)true nom nom σσσ=+ l n (1)tr u e n o m εε=+ 真实应变是由弹性应变和塑性应变组成的，定义塑性材料时，需用到塑性应变，其表达式为：1true pl true e true E σεεεε=-=-Abaqus 分析结果中对应的变量：真实应力：S,Mises 真实应变：对几何非线性问题，输出的是对数应变LE;几何线性问题，输出的是总应变E 塑性应变：等效塑性应变PEEQ ，塑性应变量PEMAG ，塑性应变分量PE 弹性应变：EE名义应变：NE在abaqus standard 中无法模拟构建塑性变形过大而破坏的过程弹塑性分析的基本方法：理想塑性：应力不变，应变持续增加；应尽可能的使材料的最大真实应力和塑性应变大于模型可能出现的应力应变值解决弹塑性分析中的收敛问题：在弹塑性材料商施加载荷时，如果此载荷会造成很大的局部变形（使用点载荷时尤其容易出现此问题），可能造成收敛问题。

粘弹性材料本构模型的研究第23卷第6期高分子材料科学与工程V o l.23,N o .62020年11月POL Y M ER M A T ER I AL S SC IEN CE AND EN G I N EER I N GN ov .2020粘弹性材料本构模型的研究Ξ路纯红,白鸿柏(军械工程学院,河北石家庄050003摘要:介绍了近年来建立粘弹性材料本构模型的方法。

目前主要有两种方法:利用现有本构模型;对粘弹性材料进行试验研究,拟合实验曲线。

关键词:粘弹性材料;本构模型中图分类号:O 631.2+1文献标识码:A 文章编号:100027555(20200620028204随着化学化工和材料工业的发展,粘弹性材料被广泛应用于航空航天、机械工程、高层建筑、车辆工程以及家用电器等领域。

研究粘弹性材料的力学性能,使其在工程应用中发挥良好的阻尼性能和耗散性能,关键是构建能够精确描述材料本构关系的粘弹性本构模型。

然而粘弹性材料的力学性能如剪切模量、损耗模量、损耗因子等受环境温度、振动频率、应变幅值等影响很大,因此,其本构关系的建立将非常复杂。

本文将对近年来粘弹性材料本构模型的研究成果进行简要的综述,并对今后的研究趋势提出几点建议。

1利用现有模型1.1粘弹性本构模型由于粘弹性材料的力学性能如剪切模量、损耗模量、损耗因子等通常与环境温度、振动频率、应变幅值等有关,因此粘弹性材料的本构关系将是复杂的。

国内外许多学者对此进行了研究,目前常用的粘弹性材料本构模型如下。

1.1.1M axw ll 模型:M axw ell 模型认为,粘弹性材料可以等效为一个弹簧和一个粘壶元件相串联而成,其本构关系为:Σ(t +p 1Σα(t =q 1Χα(t (1式中:Σ(t 和Χ(t ——粘弹性材料的剪应力和剪应变;p 1和q 1——由粘弹性材料性能确定的系数。

在简谐应变的激励下,由本构关系(1式可得:式中:G 1、G 2——储能模量(剪切模量和损耗模量;Γ——损耗因子,用于描述粘弹性材料的阻尼性能,Γ越大,材料阻尼性能越好,Γ越小,材料阻尼性能越差。