§1 定积分的概念

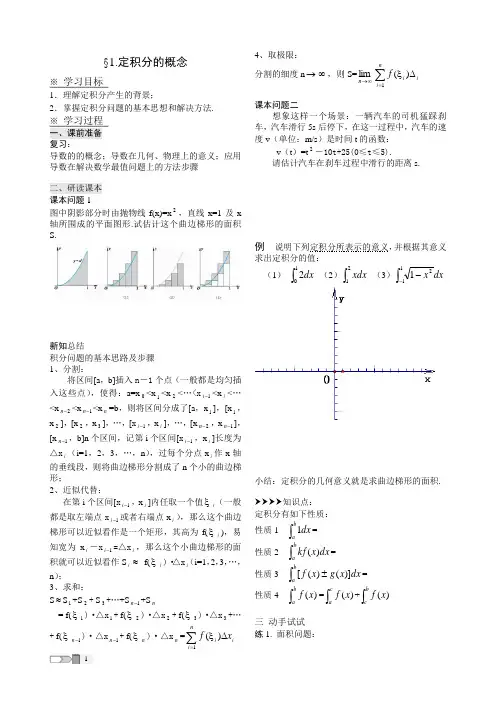
§1.定积分的概念※ 学习目标1．理解定积分产生的背景；2．掌握定积分问题的基本思想和解决方法. ※ 学习过程 一、课前准备 复习：导数的的概念；导数在几何、物理上的意义；应用导数在解决数学最值问题上的方法步骤二、研读课本 课本问题1图中阴影部分时由抛物线f(x)=x 2，直线x=1及x 轴所围成的平面图形.试估计这个曲边梯形的面积S.新知总结积分问题的基本思路及步骤 1、分割：将区间[a ，b]插入n －1个点（一般都是均匀插入这些点），使得：a=x 0<x 1<x 2<…<x 1-i <x i <…<x 2-n <x 1-n <x n =b ，则将区间分成了[a ，x 1]，[x 1，x 2]，[x 2，x 3]，…，[x 1-i ，x i ]，…，[x 2-n ，x 1-n ]，[x 1-n ，b]n 个区间，记第i 个区间[x 1-i ，x i ]长度为△x i （i=1，2，3，…，n ），过每个分点x i 作x 轴的垂线段，则将曲边梯形分割成了n 个小的曲边梯形；2、近似代替：在第i 个区间[x 1-i ，x i ]内任取一个值ξi （一般都是取左端点x 1-i 或者右端点x i ），那么这个曲边梯形可以近似看作是一个矩形，其高为f(ξi )，易知宽为x i －x 1-i =△x i ，那么这个小曲边梯形的面积就可以近似看作S i ≈ f(ξi )·△x i （i=1，2，3，…，n ）；3、求和：S ≈S 1+S 2+ S 3+…+S 1-n +S n = f(ξ1)·△x 1+ f(ξ2)·△x 2+ f(ξ3)·△x 3+…+ f(ξ1-n )·△x 1-n + f(ξn )·△x n =∑=∆ξni i i x f 1)(4、取极限：分割的细度n →∞，则S=∞→n lim∑=∆ξni iif 1)(课本问题二想象这样一个场景：一辆汽车的司机猛踩刹车，汽车滑行5s 后停下，在这一过程中，汽车的速度v （单位：m/s ）是时间t 的函数：v （t ）=t 2－10t+25(0≤t ≤5).请估计汽车在刹车过程中滑行的距离s.例 说明下列定积分所表示的意义，并根据其意义求出定积分的值： （1）⎰12dx （2）⎰21xdx （3）⎰--1121dx x小结：定积分的几何意义就是求曲边梯形的面积.知识点： 定积分有如下性质：性质1⎰ba dx 1=性质2 ⎰b a dx x kf )(=性质3 ⎰±b a dx x g x f )]()([=性质4 ⎰b ax f )(=⎰cax f )(+⎰bcx f )(三 动手试试 练1. 面积问题：设S 表示由曲线y=x ，直线x=1以及x 轴所围成平面图形的面积.(1）画出该平面图形；（2）试估计该平面图形的面积，并写出估计值的误差.练2. 做功问题一根弹性系数为0.4N/cm 的弹簧，其拉力F 随着弹簧拉伸的长度x 的变化而不断变化，根据胡克定律可知：F=F(x)=0.4x.如图所示，弹簧的一端固定在墙上，另一端固定在物体上，在不考虑摩擦力的情况下物体在力F 作用下匀速移动，从原来位置 移动10cm.估计这一过程中拉力所做的功W.练3．用图形表示下列定积分： （1）⎰102dx x （2）⎰21ln xdx （3）⎰-11dx e x※ 总结提升 学习小结1. 积分问题的基本思路及步骤：1、分割；2、近似代替；3、求和；4取极限． 2. 积分的几何意义就是求曲边梯形的面积． ※ 课后练习：（1-4选择题）1．利用定积分的几何意义求下列定积分（1）⎰212xdx （2）⎰-224dx x（3）⎰-11dx x2．已知⎰10dx e x=e ，⎰102dx x ，求下列定积分：（1）⎰+12)(dx x e x（2）⎰-12)2(dx x e x3．如果汽车在某一段时间内的速度函数为v （t ）=20t ，0≤t ≤5，试估计汽车在这段时间内走过的距离，并写出估计值的误差.4．设力F （单位：N ）的方向与抛物线运动的方向一致，力的大小随着物体走过的路程x （单位：m ）而变化，可以表示为F=F(x)=x11,估计力F 在0—10m 这段路程内所做的功，要求误差不超过1N ·m.。

§1定积分的概念学习目标 1.了解“以直代曲”，“以不变代变”的思想方法，会求曲边梯形的面积.2.了解定积分的概念，会用定义求定积分.3.理解定积分的几何意义，并掌握定积分的基本性质．知识点一曲边梯形的面积思考如图，为求由抛物线y＝x2与直线x＝1，y＝0所围成的平面图形的面积S，图形与我们熟悉的“直边图形”有什么区别？答案已知图形是由直线x＝1，y＝0和曲线y＝x2所围成的，可称为曲边梯形，曲边梯形的一条边为曲线段，而“直边图形”的所有边都是直线段．梳理由直线x＝a，x＝b(a≠b)，y＝0和曲线y＝f(x)所围成的平面图形称为曲边梯形，如图中阴影部分所示．求曲边梯形的面积的步骤(1)分割：将区间[a，b]n等分；(2)计算：过剩估计值S 1＝⎣⎢⎡ f ⎝ ⎛⎭⎪⎫a ＋b －a n ＋f ⎝ ⎛⎭⎪⎫a ＋2(b －a )n⎦⎥⎤＋…＋f ⎝⎛⎭⎪⎫a ＋n (b －a )n ×b －an ；不足估计值S 2＝⎣⎢⎡ f (a )＋f ⎝⎛⎭⎪⎫a ＋b －a n ＋f ⎝ ⎛⎭⎪⎫a ＋2(b －a )n⎦⎥⎤＋…＋f ⎝ ⎛⎭⎪⎫a ＋(n －1)(b －a )n ×b －an .(3)近似代替：无论用S 1还是用S 2表示曲边梯形的面积，误差都不会超过S 1－S 2. 知识点二 定积分的概念一般地，给定一个在区间[a ，b ]上的函数y ＝f (x )，其图像如图所示．(1)将[a ，b ]区间分成n 份，分点为：a ＝x 0<x 1<x 2<…<x n －1<x n ＝b .第i 个小区间为[x i －1，x i ]，设其长度为Δx i ，在这个小区间上取一点ξi ，使f (ξi )在区间[x i －1，x i ]上的值最大，设S ＝∑i ＝1nf (ξi )Δx i .在这个小区间上取一点ζi ，使f (ζi )在区间[x i －1，x i ]上的值最小，设s ＝∑i ＝1nf (ζi )Δx i .如果每次分割后，最大的小区间的长度趋于0，S 与s 的差也趋于0，此时S 与s 同时趋于某一个固定的常数A ，容易验证，在每个小区间[x i －1，x i ]上任取一点δ1，S ′＝∑i ＝1nf (δi )Δx i 的值也趋于该常数A ，我们称A 是函数y ＝f (x )在区间[a ，b ]上的定积分，记作ʃba f (x )d x ，即ʃb a f (x )d x ＝A .(2)ʃb a f (x )d x 中符号的意义知识点三 定积分的几何意义、物理意义 (1)定积分的几何意义当f (x )≥0时，ʃb a f (x )d x 表示的是y ＝f (x )与x ＝a ，x ＝b 和x 轴所围曲边梯形的面积． (2)定积分的物理意义当f (x )表示速度关于时间x 的函数时，ʃb a f (x )d x 表示的是运动物体从 x ＝a 到x ＝b 时所走过的路程．知识点四 定积分的性质 (1)ʃb a 1d x ＝b －a .(2)ʃb a kf (x )d x ＝k ʃb a f (x )d x (k 为常数)． (3)ʃb a [f (x )±g (x )]d x ＝ʃb a f (x )d x ±ʃb a g (x )d x . (4)ʃb a f (x )d x ＝ʃc a f (x )d x ＋ʃb c f (x )d x (其中a <c <b )．1．当n 很大时，函数f (x )＝x 2在区间⎣⎢⎡⎦⎥⎤i －1n ，i n 上的值，只能用⎝⎛⎭⎫i n 2近似代替．( × ) 2．定积分ʃb a f (x )d x 的几何意义是介于x 轴、函数f (x )的图像以及直线x ＝a ，x ＝b 之间各部分面积的代数和，在x 轴上方的面积取正号，在x 轴下方的面积取负号．( √ ) 3．曲边梯形的面积S ＝ʃb a f (x )d x ；变速直线运动的位移s ＝()21d t t t t ⎰v ；变力做功W ＝ʃbaF (r )d r .( √)类型一 定积分的定义及应用例1 求抛物线y ＝x 2与直线x ＝0，x ＝1，y ＝0所围成的平面图形的面积S .⎣⎡⎦⎤参考公式12＋22＋…＋n 2＝16n (n ＋1)(2n ＋1)考点 求曲边梯形的面积问题 题点 求曲线梯形的面积问题 解 (1)分割：在区间[0,1]上等间隔地插入n －1个点，将它等分成n 个小区间，即⎣⎡⎦⎤0，1n ，⎣⎡⎦⎤1n ，2n ，…，⎣⎢⎡⎦⎥⎤n －1n ，1.记第i 个区间为⎣⎢⎡⎦⎥⎤i －1n ，i n (i ＝1,2，…，n )，其长度为Δx ＝i n －i －1n ＝1n .分别过上述n －1个分点作x 轴的垂线，把曲边梯形分成n 个小曲边梯形，它们的面积记作ΔS 1，ΔS 2，…，ΔS n ，则S ＝∑i ＝1nΔS i .(2)近似代替：记f (x )＝x 2.当n 很大时，即Δx 很小时，在区间⎣⎢⎡⎦⎥⎤i －1n ，i n 上可以认为f (x )＝x 2的值变化很小，近似地等于一个常数，不妨认为它近似地等于左端点i －1n 处的函数值f ⎝ ⎛⎭⎪⎫i －1n .这样在区间⎣⎢⎡⎦⎥⎤i －1n ，i n 上，用小矩形的面积ΔS i ′近似地代替ΔS i ，即在局部小范围内“以直代曲”，则有 ΔS i ≈ΔS i ′＝f ⎝ ⎛⎭⎪⎫i －1n Δx ＝⎝ ⎛⎭⎪⎫i －1n 2·Δx ＝⎝ ⎛⎭⎪⎫i －1n 2·1n (i ＝1,2，…，n )．① (3)求和：由①得S n ＝∑i ＝1nΔS i ′＝∑i ＝1nf ⎝ ⎛⎭⎪⎫i －1n Δx ＝∑i ＝1n ⎝ ⎛⎭⎪⎫i －1n 2·1n ＝0·1n ＋⎝⎛⎭⎫1n 2·1n ＋…＋⎝ ⎛⎭⎪⎫n －1n 2·1n ＝1n 3[12＋22＋…＋(n －1)2]＝1n 3·n (n －1)(2n －1)6＝13⎝⎛⎭⎫1－1n ⎝⎛⎭⎫1－12n ，从而得到S 的近似值， 即S ≈S n ＝13⎝⎛⎭⎫1－1n ⎝⎛⎭⎫1－12n .② (4)取极限：分别将区间[0,1]等分成8,16,20，…等份时，可以看到随着n 的不断增大，即Δx 越来越小时，S n ＝13⎝⎛⎭⎫1－1n ⎝⎛⎭⎫1－12n 越来越趋近于S ，而当n 趋向于＋∞时，②式无限趋近于13，即所求面积为13. 反思与感悟 求曲边梯形的面积 (1)思想：以直代曲．(2)步骤：分割→近似代替→求和→取极限． (3)关键：近似代替．(4)结果：分割越细，面积越精确． (5)求和时可用一些常见的求和公式，如1＋2＋3＋…＋n ＝n (n ＋1)2，12＋22＋32＋…＋n 2＝n (n ＋1)(2n ＋1)6，13＋23＋33＋…＋n 3＝⎣⎢⎡⎦⎥⎤n (n ＋1)22.跟踪训练1 利用定积分的定义，求ʃ10x d x . 考点 求曲边梯形的面积问题 题点 求曲边梯形的面积问题 解 (1)分割：将区间[0,1]分为n 等份，形成n 个小区间[x i －1，x i ]＝⎣⎢⎡⎦⎥⎤i －1n ，i n (i ＝1,2，…，n )，且每个小区间的长度为Δx ＝1n .(2)近似代替：取ξi ＝in(i ＝1,2，…，n )，则S n ＝∑i ＝1n f ⎝⎛⎭⎫i n ·Δx ＝∑i ＝1n i n ·1n＝1n 2∑i ＝1n i ＝1n 2·n (n ＋1)2＝n ＋12n. (3)取极限：ʃ10x d x ＝lim n →＋∞S n ＝lim n →＋∞n ＋12n ＝12. 类型二 利用定积分的性质求定积分例2 已知ʃ10x 3d x ＝14，ʃ21x 3d x ＝154，ʃ21x 2d x ＝73，ʃ42x 2d x ＝563，求下列各式的值． (1)ʃ20(3x 3)d x ；(2)ʃ41(6x 2)d x ；(3)ʃ21(3x 2－2x 3)d x .考点 定积分性质的应用 题点 定积分性质的应用解 (1)ʃ20(3x 3)d x ＝3ʃ20x 3d x ＝3()ʃ10x 3d x ＋ʃ21x 3d x＝3×⎝⎛⎭⎫14＋154＝12.(2)ʃ41(6x 2)d x ＝6ʃ41x 2d x ＝6()ʃ21x 2d x ＋ʃ42x 2d x＝6×⎝⎛⎭⎫73＋563＝126.(3)ʃ21(3x 2－2x 3)d x ＝ʃ21(3x 2)d x －ʃ21(2x 3)d x＝3ʃ21x 2d x －2ʃ21x 3d x ＝3×73－2×154＝－12. 反思与感悟 若函数f (x )的奇偶性已经明确，且f (x )在[－a ，a ]上连续，则 (1)若函数f (x )为奇函数，则ʃa －a f (x )d x ＝0.(2)若函数f (x )为偶函数，则ʃa －a f (x )d x ＝2ʃa 0f (x )d x .跟踪训练2 若f (x )＝⎩⎪⎨⎪⎧2x －1，－1≤x <0，e －x ，0≤x ≤1，且ʃ0－1(2x －1)d x ＝－2，ʃ10e－x d x ＝1－e －1， 求ʃ1－1f (x )d x .考点 定积分性质的应用 题点 定积分性质的应用解 ʃ1－1f (x )d x ＝ʃ0－1f (x )d x ＋ʃ10f (x )d x ＝ʃ0－1(2x －1)d x ＋ʃ10e －x d x＝－2＋1－e －1＝－(e －1＋1)．类型三 利用定积分的几何意义求定积分 例3 用定积分的几何意义求下列各式的值． (1)ʃ1－14－x 2d x ；(2)π2π2sin d x x -⎰.考点 定积分几何意义的应用 题点 定积分几何意义的应用 解 (1)由y ＝4－x 2得x 2＋y 2＝4(y ≥0)，其图像如图所示．ʃ1－14－x 2d x 等于圆心角为60°的弓形CED 的面积与矩形ABCD 的面积之和，S 弓形CED ＝π×22×16－12×2×3＝2π3－3，S 矩形ABCD ＝AB ·BC ＝23， ∴ʃ1－14－x 2d x ＝23＋2π3－3＝2π3＋ 3. (2)∵函数y ＝sin x 在x ∈⎣⎡⎦⎤－π2，π2上是奇函数， ∴π2π2sin d x x -⎰＝0.反思与感悟 利用定积分所表示的几何意义求ʃb af (x )d x 的值的关键是确定由曲线y ＝f (x )，直线x ＝a ，直线x ＝b 及x 轴所围成的平面图形的形状．常见形状是三角形、直角梯形、矩形、圆等可求面积的平面图形．跟踪训练3 求定积分：ʃ20(4－(x －2)2－x )d x .考点 定积分几何意义的应用 题点 定积分几何意义的应用 解 ʃ204－(x －2)2d x 表示圆心在(2,0)，半径等于2的圆的面积的14，即ʃ204－(x －2)2d x ＝14×π×22＝π.ʃ20x d x 表示底和高都为2的直角三角形的面积， 即ʃ20x d x ＝12×22＝2. ∴原式＝ʃ204－(x －2)2d x －ʃ20x d x ＝π－2.1．在求由函数y ＝1x的图像与直线x ＝1，x ＝2，y ＝0所围成的平面图形的面积时，把区间[1,2]等分成n 个小区间，则第i 个小区间为( ) A.⎣⎡⎦⎤i －1n ，i nB.⎣⎡⎦⎤n ＋i －1n ，n ＋i nC ．[i －1，i ] D.⎣⎡⎦⎤i n ，i ＋1n考点 定积分的概念 题点 定积分的概念 答案 B解析 把区间[1,2]等分成n 个小区间后，每个小区间的长度为1n ，且第i 个小区间的左端点不小于1.故选B.2．设函数f (x )在区间[a ，b ]上连续，用分点a ＝x 0<x 1<…<x i －1<x i <…<x n ＝b 把区间[a ，b ]等分成n 个小区间，在每个小区间[x i －1，x i ]上任取一点ξi (i ＝1,2，…，n )，作和式S n ＝∑i ＝1nf (ξi )Δx i ，其中Δx i 为小区间的长度，那么和式S n 的大小( )A ．与f (x )和区间[a ，b ]有关，与分点的个数n 和ξi 的取法无关B ．与f (x )、区间[a ，b ]和分点的个数n 有关，与ξi 的取法无关C ．与f (x )、区间[a ，b ]和ξi 的取法有关，与分点的个数n 无关D ．与f (x )、区间[a ，b ]、分点的个数n 和ξi 的取法都有关 考点 定积分的概念 题点 定积分的概念 答案 D3．下列值等于1的是( )A ．ʃ10x d xB ．ʃ10(x ＋1)d xC ．ʃ101d xD ．ʃ1012d x 考点 定积分的几何意义及性质 题点 定积分的几何意义 答案 C解析 ʃ10x d x ＝12×1×1＝12，ʃ10(x ＋1)d x ＝12×(1＋2)×1＝32，ʃ101d x ＝1×1＝1，ʃ1012d x ＝12×1＝12. 4．汽车以10米/秒的速度行驶，在某处需要减速停车，设汽车以－2米/秒2的加速度刹车，若把刹车时间5等分，则从开始刹车到停车，汽车刹车距离的过剩估计值(取每个小区间的左端点对应的函数值)为( )A ．80米B ．60米C ．40米D ．30米 考点 变速运动的路程问题 题点 变速运动的路程问题 答案 D解析 由题意知v (t )＝v 0＋at ＝10－2t ，令v (t )＝0，得t ＝5，即当t ＝5秒时，汽车将停车．将区间[0,5]5等分，用每个小区间的左端点的函数值近似替代每个小区间上的平均速度，可得汽车刹车距离的过剩估计值S ＝(10＋10－2×1＋10－2×2＋10－2×3＋10－2×4)×1＝30(米)．5．计算：3π2π2(25sin )d x x ⎰－.考点 定积分的几何意义及性质 题点 定积分的几何意义 解 由定积分的几何意义，得3π2π22d x ⎰＝⎝⎛⎭⎫3π2－π2×2＝2π.由定积分的几何意义，得3π2π2sin d x x ⎰＝0.所以3π2π2(25sin )d x x ⎰－＝3π2π22d x ⎰－53π2π2sin d x x ⎰＝2π.1．定积分ʃb a f (x )d x 是一个和式∑i ＝1nb －anf (ξi )的极限，是一个常数． 2．可以利用“分割、近似代替、求和、取极限”求定积分．对于一些特殊函数，也可以利用几何意义求定积分．3．定积分的几何性质可以帮助简化定积分运算.一、选择题1．把区间[1,3] n 等分，所得n 个小区间的长度均为( ) A.1n B.2n C.3n D.12n 考点 求曲边梯形的面积问题 题点 求曲边梯形的面积问题 答案 B解析 区间[1,3]的长度为2，故n 等分后，每个小区间的长度均为2n .2．当n 的值很大时，函数f (x )＝x 2在区间⎣⎡⎦⎤i －1n ，i n 上的值可以用下列函数值近似代替的是( )A ．f ⎝⎛⎭⎫1nB ．f ⎝⎛⎭⎫2nC ．f ⎝⎛⎭⎫i nD ．f (0) 考点 定积分的概念 题点 定积分的概念 答案 C3．下列命题不正确的是( )A ．若f (x )是连续的奇函数，则ʃa －a f (x )d x ＝0B ．若f (x )是连续的偶函数，则ʃa －a f (x )d x ＝2ʃa0f (x )d xC ．若f (x )在[a ，b ]上连续且恒正，则ʃb a f (x )d x >0D ．若f (x )在[a ，b ]上连续且ʃb a f (x )d x >0，则f (x )在[a ，b ]上恒正 考点 定积分的几何意义及性质 题点 定积分性质 答案 D解析 A 项，因为f (x )是奇函数，图像关于原点对称，所以x 轴上方的面积和x 轴下方的面积相等，故积分是0，所以A 项正确；B 项，因为f (x )是偶函数，图像关于y 轴对称，故y 轴两侧的图像都在x 轴上方或下方且面积相等，故B 项正确；由定积分的几何意义知，C 项显然正确；D 项，f (x )也可以小于0，但必须有大于0的部分，且f (x )>0的曲线围成的面积比f (x )<0的曲线围成的面积大．4．与定积分3π20sin d x x ⎰相等的是( ) A. 3π20sin d x x ⎰ B. 3π20sin d x x ⎰C ．ʃπ0sin x d x －3π2πsin d x x ⎰D ．π20sin d x x ⎰＋3π2πsin d x x ⎰考点 定积分的几何意义及性质题点 定积分性质答案 C解析 当x ∈[0，π]时，sin x ≥0；当x ∈⎝⎛⎦⎤π，3π2时，sin x <0.∴由定积分的性质可得，3π20sin d x x ⎰＝ʃπ0|sin x |d x ＋3π2πsin d x x ⎰＝ʃπ0sin x d x ＋3π2π(sin )d x x ⎰－＝ʃπ0sin x d x －3π2πsin d x x ⎰.5．下列各阴影部分的面积S 不可以用S ＝ʃb a [f (x )－g (x )]d x 求出的是()考点 定积分的几何意义及性质题点 定积分的几何意义答案 B解析 定积分S ＝ʃb a [f (x )－g (x )]d x 的几何意义是求函数f (x )与g (x )之间的阴影部分的面积，必须注意f (x )的图像要在g (x )的图像上方．对照各选项可知，B 项中f (x )的图像不全在g (x )的图像上方，故选B.6．由直线y ＝x ，y ＝－x ＋1及x 轴围成的平面图形的面积为( )A ．ʃ10[(1－y )－y ]d yB ．120[(1)]d x x x ⎰－＋－C ．120d x x ⎰＋112(1)d x x ⎰－＋D ．ʃ10[x －(－x ＋1)]d x考点 定积分的几何意义及性质题点 定积分的几何意义答案 C解析 联立⎩⎪⎨⎪⎧y ＝x ，y ＝－x ＋1，解得⎩⎨⎧ x ＝12，y ＝12，故A ⎝⎛⎭⎫12，12. 由图知阴影部分的面积可表示为120d x x ⎰＋112(1)d x x ⎰－＋.7．设a ＝ʃ10x 13d x ，b ＝ʃ10x 2d x ，c ＝ʃ10x 3d x ，则a ，b ，c 的大小关系是() A ．a >b >c B ．a >c >bC ．a ＝b >cD ．c >a >b考点定积分几何意义的应用题点定积分几何意义的应用答案 A解析根据定积分的几何意义，易知ʃ10x3d x<ʃ10x2d x<ʃ10x 13d x，即a>b>c，故选A.8．若ʃa－a|56x|d x≤2 016，则正数a的最大值为() A．6 B．56C．36 D．2 016考点定积分几何意义的应用题点定积分几何意义的应用答案 A解析由ʃa－a|56x|d x＝56ʃa－a|x|d x≤2 016，得ʃa－a|x|d x≤36，∵ʃa－a|x|d x＝a2，∴a2≤36，即0<a≤6.故正数a的最大值为6.二、填空题9．若ʃ1012f(x)d x＝1，ʃ－13f(x)d x＝2，则ʃ1－1f(x)d x＝________.考点定积分性质的应用题点定积分性质的应用答案8 3解析∵ʃ1012f(x)d x＝12ʃ1f(x)d x＝1，∴ʃ10f(x)d x＝2.又ʃ0－13f(x)d x＝3ʃ0－1f(x)d x＝2，∴ʃ0－1f(x)d x＝2 3.∴ʃ1－1f(x)d x＝ʃ0－1f(x)d x＋ʃ10f(x)d x＝23＋2＝83.10．如图所示的阴影部分的面积用定积分表示为________．考点 定积分的几何意义及性质题点 定积分的几何意义答案 ʃ2－4x 22d x 11．定积分ʃ10(2＋1－x 2)d x ＝________.考点 定积分几何意义的应用题点 定积分几何意义的应用答案 2＋π4解析 原式＝ʃ102d x ＋ʃ101－x 2d x . 因为ʃ102d x ＝2，ʃ101－x 2d x ＝π4， 所以ʃ10(2＋1－x 2)d x ＝2＋π4. 12．已知f (x )是一次函数，其图像过点(3,4)且ʃ10f (x )d x ＝1，则f (x )的解析式为________． 考点 定积分几何意义的应用题点 定积分几何意义的应用答案 f (x )＝65x ＋25解析 设f (x )＝ax ＋b (a ≠0)，∵f (x )图像过(3,4)点，∴3a ＋b ＝4.又ʃ10f (x )d x ＝ʃ10(ax ＋b )d x ＝a ʃ10x d x ＋ʃ10b d x ＝12a ＋b ＝1. 解方程组⎩⎪⎨⎪⎧ 3a ＋b ＝4，12a ＋b ＝1，得⎩⎨⎧ a ＝65，b ＝25.∴f (x )＝65x ＋25.三、解答题13．已知f (x )＝⎩⎪⎨⎪⎧ x ，x ∈[0，2)，4－x ，x ∈[2，3)，52－x 2，x ∈[3，5]，求f (x )在区间[0,5]上的定积分．考点 定积分几何意义的应用题点 定积分几何意义的应用解 如图画出函数f (x )的图像．由定积分的几何意义得ʃ20x d x ＝12×2×2＝2， ʃ32(4－x )d x ＝12×(1＋2)×1＝32， ʃ53⎝⎛⎭⎫52－x 2d x ＝12×2×1＝1. 所以ʃ50f (x )d x ＝ʃ20x d x ＋ʃ32(4－x )d x ＋ʃ53⎝⎛⎭⎫52－x 2d x ＝2＋32＋1＝92. 四、探究与拓展14．若定积分ʃm －2－x 2－2x d x ＝π4，则m 等于( ) A ．－1B ．0C ．1D ．2 考点 定积分几何意义的应用题点 定积分几何意义的应用答案 A解析 根据定积分的几何意义知，定积分ʃm －2－x 2－2x d x 的值就是函数y ＝－x 2－2x 的图像与x 轴及直线x ＝－2，x ＝m 所围成的图形的面积．y ＝－x 2－2x 是一个以(－1,0)为圆心，1为半径的半圆，其面积等于π2，而ʃm －2－x 2－2x d x ＝π4，所以m ＝－1.15.如图所示，抛物线y ＝12x 2将圆x 2＋y 2≤8分成两部分，现在向圆上均匀投点，这些点落在圆中阴影部分的概率为14＋16π，求ʃ20⎝⎛⎭⎫8－x 2－12x 2d x .考点 定积分几何意义的应用题点 定积分几何意义的应用解 解方程组⎩⎪⎨⎪⎧x 2＋y 2＝8，y ＝12x 2，得x ＝±2. ∴阴影部分的面积为ʃ2－2⎝⎛⎭⎫8－x 2－12x 2d x . ∵圆的面积为8π， ∴由几何概型可得阴影部分的面积是8π·⎝⎛⎭⎫14＋16π＝2π＋43. 由定积分的几何意义得，ʃ20⎝⎛⎭⎫8－x 2－12x 2d x ＝12ʃ2－2⎝⎛⎭⎫8－x 2－12x 2d x ＝π＋23.。

§1 定积分的概念学习目标1.通过求曲边梯形的面积和变速直线运动的路程，了解定积分的背景；2.了解定积分的概念，能用定积分法求简单的定积分．3.理解掌握定积分的几何意义和性质； 学习指导 20 预习教材P 75~ P 81，找出疑惑之处问题：求图中阴影部分是由抛物线2y x =，直线1=x 以及x 轴所围成的平面图形的面积S 。

一般地，设函数()f x 在区间[,]a b 上连续，用分点0121i i n a x x x x x x b -=<<<<<<<= 将区间[,]a b 等分成n 个小区间,在每个小区间[]1,i i x x -上取一点()1,2,,i i n ξ= ,作和式：()()11nni i i i b af x f nξξ==-∆=∑∑当n →+∞时，上述和式无限接近某个常数，这个常数叫做函数()f x 在区间[,]a b 上的定积分。

记为：()baf x dx ⎰， 即()baf x dx ⎰=()i ni n f nab ξ∑=∞→-1lim 其中函数()f x 叫做 ，x 叫做 变量，区间[,]a b 为 区间，b 叫做积分 ，a 叫做积分 。

说明：（1）定积分()baf x dx ⎰是一个常数 ；（2）曲边图形面积：()baS f x dx =⎰； 变速运动路程21()t t S v t dt =⎰.性质11badx =⎰性质2 ()ba kf x dx =⎰性质312[()()]baf x f x dx ±=⎰性质4()()bc aaf x dx f x dx =+⎰⎰当堂练习:+20 1、定积分⎰bacdx （常数0c >）的几何意义是2、由sin y x =，0x =，2x π=，0y =所围成图形的面积写成定积分的形式是3、连续函数0)(>x f ,则当b a <时,定积分⎰badx x f )(的符号( )A.一定是正的B.一定是负的C.当b a <<0时是正的D.以上都不对 4、与定积分dx x ⎰π230sin 相等的是( )A.⎰π230sin xdx B.⎰π230sin xdxC.⎰πsin xdx -⎰ππ23sin xdx D.⎰⎰+23220sin sin πππxdx xdx5、定积分⎰badx x f )(的大小（ ）A 、与)(x f 和积分区间[]b a ,有关，与i ξ的取法无关B 、与)(x f 有关，与区间[]b a ,及i ξ的取法无关C 、与)(x f 和i ξ的取法有关，与积分区间[]b a ,无关D 、与)(x f 、区间[]b a ,和i ξ的取法都有关 6、下列等式或不等式成立的个数是（ ） ①⎰⎰=101)()(dx x f dt t f ②dx x dx x xdx ⎰⎰⎰=+ππππ220sin sin sin③dx x dx x a aa⎰⎰=-02④11dx <⎰⎰A 、1B 、2C 、3D 、4 7、计算下列定积分 （1）21(1)x dx +⎰； （2）22x dx -⎰； （3）a-⎰（0a >）；（4）()4f x dx ⎰其中(),011,134,34x x f x x x x ≤<⎧⎪=≤≤⎨⎪-<≤⎩.。