当前位置：文档之家 › 定积分定义

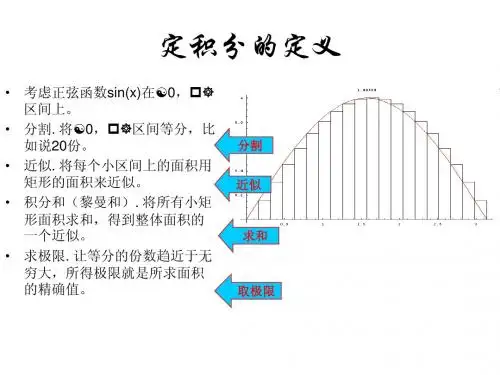
定积分定义

  • 格式：ppt
  • 大小：544.50 KB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

定积分概念的步骤

定积分概念的步骤

定积分概念的步骤定积分是微积分中的重要概念，用于求解曲线下方某一区间的面积，或求解函数在某一区间上的平均值等问题。

下面将详细介绍定积分的概念和求解的步骤。

定积分的概念：定积分是求解曲线下方某一区间的面积的数学工具，它是定义在闭区间[a,b]上的函数f(某)的一个性质，可以理解为函数f(某)在区间[a,b]上的累积效应。

定积分步骤如下：1.确定积分区间：首先需要确定定积分的积分区间，即求解的曲线下方的面积的范围。

区间一般以[a,b]表示，其中a和b为常数。

2.确定积分函数：根据具体问题，确定要计算的函数f(某)。

函数f(某)可以是一个实际问题中的物理量随时间或空间的变化函数。

3.将积分区间分成若干小区间：将积分区间[a,b]分割成若干个小区间，每个小区间的长度为∆某。

通常，分割是均匀的，即每个小区间的长度相等。

4.选择代表性点：在每个小区间中选择一个代表性点某i。

可以根据需要选择左端点、右端点、中点等。

这些代表性点将被用来求解小区间上曲线下方的面积。

5.计算小区间上的面积：根据代表性点某i，计算每个小区间上曲线下方的面积。

这可以通过求解函数f(某)在小区间上的定积分来实现。

6.求和：将每个小区间上的面积求和，得到整个积分区间[a,b]上曲线下方的总面积。

这里的求和过程可以看作是将所有小区间的面积进行累加的过程。

7.极限过程：随着小区间的个数无限增大，每个小区间的长度趋近于0，即∆某趋近于0。

这时候，计算的总面积就趋近于定积分的值。

8.计算定积分：根据定义，定积分可以通过求解函数f(某)的原函数F(某)，并在积分区间[a,b]上的两个端点处进行求值来实现。

定积分的求解可以使用积分公式、牛顿-莱布尼茨公式和数值积分等方法。

总结：定积分通过将积分区间分割成无限小的小区间，在每个小区间上计算曲线下方的面积，并将其累加，从而求得整个积分区间上的面积。

定积分的计算可以通过求解函数的原函数和积分公式来进行。

它是微积分中的重要工具，被广泛应用于物理学、经济学、统计学等领域。

定积分的概念、性质

定积分的概念、性质
*
三、定积分的性质
§5.1 定积分的概念与性质
一、定积分问题举例
演讲人姓名
二、定积分定义
一、定积分问题举例
曲边梯形 设函数yf(x)在区间[a, b]上非负、连续. 由直线xa、xb、y0及曲线yf (x)所围成的图形称为 曲边梯形, 其中曲线弧称为曲边.
曲边梯形的面积
*
观察与思考
定积分的定义
*
二、定积分定义
例1 用定积分表示极限 解 定积分的定义
*
二、定积分定义
定积分的定义
注: 设f (x)在[0, 1]上连续, 则有
*
定积分的几何意义
这是因为 曲边梯形面积 曲边梯形面积的负值
*
定积分的几何意义
各部分面积的代数和 曲边梯形面积 曲边梯形面积的负值
*
例2
在曲边梯形内摆满小的矩形, 当小矩形的宽度减少时, 小矩形面积之和与曲边梯形面积之间的误差将如何变化? 怎样求曲边梯形的面积？
*
(2)近似代替:
求曲边梯形的面积
(1)分割:
ax0< x1< x2< < xn1< xn b, Dxi=xi-xi1;
小曲边梯形的面积近似为f(xi)Dxi (xi1<xi<xi);
如果在区间[a b]上 f (x)g(x) 则
如果在区间[a b]上 f (x)0 则
性质5
推论2
性质6
设M及m分别是函数f(x)在区间[a b]上的最大值及最小值 则
例4 试证:
证明 设 则在 上, 有 即 故 即
*
性质7(定积分中值定理)
如果函数f(x)在闭区间[a b]上连 续 则在积分区间[a b]上至少存在一个点x 使下式成立 这是因为, 由性质6 ——积分中值公式 由介值定理, 至少存在一点x[a, b], 使 两端乘以ba即得积分中值公式.

定积分的概念

定积分的概念

设某质点作直线运动，速度 v v (t ) 是时间间 隔[T1 , T2 ]上 t 的一个连续函数，物体在这段时 间内所经过的路程.
S v(t )dt
T2 T1
例1 利用定义计算定积分 x 2dx.
0
1
i 解 将[0,1]n 等分，分点为 x i ，(i 1,2, , n ) n 1 小区间[ x i 1 , x i ]的长度x i ，(i 1,2, , n ) n 取 i x i ，(i 1,2,, n )
f ( x ) |在区间[a , b] 上的可积性是显然的.
（3） 设 M 及m 分别是函数
f ( x ) 在区间[a , b] 上的最大值及最小值，
则 m(b a ) a f ( x )dx M (b a ) .
b
6） (积分中值定理)若函数f ( x)在区间[a, b]上连续 . 则在[a, b]上至少存在一点 , 使得下式成立 :
o a
x1
x i 1 i x i
xn1 b
x
以 [ xi 1 , xi ]为底， (i ) 为高的小矩形面积为 f
Ai f ( i )xi
近似
曲边梯形面积的近似值为
A f ( i )xi
i 1
n
求和
当分割无限加细即小区间的最大长度 ,
max{x1 , x2 ,xn }
b
x
a f ( x )dx A
曲边梯形的面积
a f ( x )dx A
曲边梯形的面积 的负值
b
y
a
o

A2

A1
A3

b
x
它 是 介 于x 轴 、 函 数 f ( x ) 的 图 形 及 两 条 直 线 x a, x b 之 间 的 各 部 分 面 积 的数 和 ． 代 在 x 轴 上 方 的 面 积 取 正 号在 x 轴 下 方 的 面 ； 积取负号．

定积分的概念

定积分的概念
n n n n
事实上, 许多问题都可以归结为 求这种特定形式 和的极限.一般地, 我们有 如果函数f x 在区间a, b上连续, 用分点 a x 0 x1 x i1 x i x n b 将区间a, b等分成n个小区间, 在每个小区间 xi1, xi 上任取一点ξI i 1,2, ,n, 作和式 n n ba f ξ i Δx n f ξ i ,当n 时, 上述和式无 i1 i1 当函数f x 在区间a,b上连续时 这里的定义与 ,
b a
y
A
y f1x
B
D
M
y f2 x
C
N b
o
a
x
图1.5 8
探究 : 根据定积分的几何意义, 你能用定积分表 示图1.5 8 中阴影部分的面积S吗 ?
容易发现 S f1x dx f2 x dx . ,
b b a a
注意：
当f ( x) 0时，曲边梯形位于 轴下方，此时， X
面积值为圆的面积的
1 4
y
所 以
1
0
1 x dx
2

4
1 x
小结:
1.定积分是一个特定形式和的极限，其 几何意义是曲边梯形的面积，定积分的 值由被积函数，积分上限和下限所确定. 2.在实际问题中，定积分可以表示面 积、体积、路程、功等等，求定积分的 值目前有定义法和几何法两种，有时利 用定积分的性质进行计算，能简化解题
1 4 n
i
i1
n
3
1 1 1 1 2 2 4 n n 1 1 . n 4 4 n
3 3 3
2
1 2 2 i 1 2 n 4 n n 1 . i 1

第一节 定积分的概念和性质

第一节 定积分的概念和性质

x
用矩形面积近似取代曲边梯形面积
y
y
o
a
（四个小矩形）
b
x o
a
（九个小矩形）
b
x
显然，小矩形越多，矩形总面积越接近 曲边梯形面积．
观察下列演示过程，注意当分割加细时， 矩形面积和与曲边梯形面积的关系．
播放
曲边梯形如图所示， 在区间 [a , b]内插入若干
个分点，a x0 x1 x2 xn1 xn b,
a b
（2）当a b 时， f ( x )dx f ( x )dx .
a b
b
a
说明 在下面的性质中，假定定积分都存 在，且不考虑积分上下限的大小．
性质1 证
a [ f ( x ) g( x )]dx a f ( x )dx a g( x )dx .
b
b
b
b
a [ f ( x ) g( x )]dx n lim [ f ( i ) g( i )]xi 0
a f ( x )dx a g( x )dx .
b b
于是
性质5的推论： （ 2） 证
a f ( x )dx a
b
b
b
f ( x )dx . (a b)
f ( x) f ( x) f ( x) ,
a f ( x )dx a f ( x )dx a f ( x )dx ,
lim f ( i )xi lim g( i )xi
i 1 n n
a f ( x )dx a g( x )dx .
（此性质可以推广到有限多个函数作和的情况）
0 i 1 b
0 i 1

14第五章定积分(定积分的定义与性质)

14第五章定积分(定积分的定义与性质)

记 xk xk xk 1, k 1, 2,
, n, max 1k n
xk
再在每个小区间 [xk1, xk
积 f (k )xk 的和式：
]上任取一点
n
k
f (k )xk
，作乘
k 1
如果 0时,上述极限存在（即，这个极限值与 [a,b]的分割
及点i 的取法均无关），则称此极限值为函数 f (x) 在区间[a, b]
（此性质可以推广到有限多个函数作和的情况）
性质2
abkf
(
x)dx
k
b
a
f
(
x)dx
(k 为常数).
例1 下列各式不正确的是（D ）.
(A)
d
b f (x)dx d
b
f (x)dx 0
dx a
dt a
1
1
(B) f (sin x)dx f (sin t)dt
0
0
(C)
d
b
b
xf (t)dt f (x)dx
定积分 x f (t)dt 称为变上限定积分，它是 x的函数，记作(x) ，即 a
(x)
x
f (t)dt
(x [a,b]).
a
定理 1 若函数 f (x) 在区间 [a,b]上连续，则变上限定积分
(x) x f (t)dt 在区间[a,b]上可导，并且它的导数等于被积函数， a
即 (x) [ x f (t)dt] f (x) . (x) 是 函 数 f (x) 在[a,b] 的 一个 原函 a
上的定积分，记为 b
n
a
f (x)dx lim 0 k 1
f (k )xk .
积分上限

定积分的基本概念

定积分的基本概念

方法与手段导入幻灯幻灯幻灯幻灯详讲详讲详讲幻灯下面就是根据这个思想用计算机对其划分过程进行了模拟，通过观察我们可以发现其面积在分割份数特别多的时候已经非常的接近我们的曲边梯形面积了。

事实上我们如果对其切割的份数取极限，让切割的份数趋于无穷，这个极限值就是我们要求的曲边梯形的面积值。

好，下面，我们把曲边梯形的求解过程用数学的方法描述一下。

解决步骤：大化小：在区间[a,b]中任意插入n −1个分点a =x 0<x 1<x 2<⋯<x n−1<x n−1=b ，用直线x =x i 将一个曲边梯形分成n 个小的曲边梯形；常带变：在第k 个窄边梯形上任取ξk ∈[x k−1,x k ]作以[x k−1,x k ]为底，f(ξk )为高的小矩形，并以此小矩形面积近似代替相应窄曲边梯形面积∆S k ，得∆S k ≈f (ξk )∆x k (∆x k =x k −x k−1,k =1,2,⋯n) 近似和：S =∑∆S k n k=1≈∑f(ξk )∆x k n k=1取极限：令λ=max {∆x 1,∆x 2⋯,∆x n } S =lim λ→0∑∆S k n k=1=lim λ→0∑f(ξk )∆x k n k=1这样我们就可以求出曲边梯形的面积，我们再看一个定积分问题例子。

（2）变速直线运动的路程：设某物体做直线运动，已知()v v t =在区间[1T ,2T ]上t 的连续函数，且()0v t ≥，求在这段时间内物体所经过的路程s 。

考虑：当()0y f x C ==≥，()0v v t C ==≥时（其中C 为常数），上面问题的求解。

在解决这个问题之前我们先分析一下这个问题与上个问题之间的关系，我们可以发现其实求路程和求面积本身是同一类问题，变化的无非是函数名，区间名称，本质上是一样的，我们其实只需做一个按照上面的思路做一个变量替换就可以了，具体的解决步骤是。

解决步骤： 详讲 总结λ→0是个障碍，我们能不能把λ→0替换掉？其实把[0,1]区间n 等分，λ=1n →0，其实就是n →+∞，lim n→+∞∑(k n )21n n k=1，要求这个极限我需要先求∑(k n )21n n k=1，化简一下可以得到1n 3∑k 2n k=1，∑k 2n k=1=？，∑k 2n k=1=16n(n +1)(2n +1)，lim n→+∞∑(k n )21n n k=1=lim n→+∞n(n+1)(2n+1)6n 3=13。

不定积分与定积分的定义

不定积分与定积分的定义

不定积分与定积分的定义
(1)
定积分和不定积分是数学中一类常见的概念，它们都可以用来
估算某个面积以及积分。

不定积分又称为抽象积分，是用来估算某个
积分在某个空间内某个函数的值的方法，而定积分就是在一定的函数
和某个限定区间求这个函数的定积分的过程。

不定积分是用来估算函数在某段时间内所取值的积分，它可以用
来估算面积或者某函数在一定空间内的值。

它通常以d比如dx来表示，这里的d意味着对函数求偏导数，而dx表示求偏导时要将函数中的某
变量恒定，通过求偏导数可以估计函数在这一空间内的积分值。

定积分则是在某个限定区间内求函数的一个积分，它的定义是把
这一段区间分解成多个小的区间，积分的值是将每一小段的值加起来
的总和。

它的计算方法有很多种，比如梯形法、辛普森法、龙贝格法等，不同的计算方法都有适合的应用场景。

总的来说，定积分和不定积分都是一类比较常见的概念，它们都
可以用来估算某函数在某一空间内所取值的积分，不定积分用来估计
某函数在某时间段内平均取什么值，而定积分则是在某区间求这个函
数的定积分值，可以综合使用来估算一个完整的函数面积，从而求出
有意义的面积概念。

4(1)定积分的概念与性质

4(1)定积分的概念与性质

今后将经常利用定积分与变量记号无关性 进行推理.
12
定积分的概念与性质
3、定积分的几何意义和物理意义
(1). 几何意义
f ( x) 0,
b
f ( x)dx A
曲边梯形的面积
a
f ( x) 0, b f ( x)dx A 曲边梯形的面积
a
y
的负值
f (x)
A1
a
A2 O
A3
bx
b
a f ( x)dx A1 A2 A3
13
定积分的概念与性质
b f ( x)dx几何意义 a 它是介于x轴、函数 f (x) 的图形及两条
直线 x =a, x = b之间的 各部分面积的代数和.
在 x 轴上方的面积取正号; 在 x 轴下方的面积
取负号.
y
f (x)


a
O
b
b
a g( x)dx a f ( x)dx 0
于是
b
b
f ( x)dx g( x)dx
a
a
23
定积分的概念与性质
比较下列积分的大小.
(1)
1 x2dx
0
1 x3dx
0

(2) 2 xdx 0

2 sin xdx
0
(3) 0 exdx 1
25
定积分的概念与性质
(估值定理)
性质6 设M和m 分别是函数f ( x)在[a,b]上的
最大值及最小值.
则 m(b a)
b
f ( x)dx M (b a)
a
证 m f (x) M

定积分的定义

定积分的定义
定积分的定义
• 考虑正弦函数sin(x)在0， 区间上。 • 分割. 将0，区间等分，比 如说20份。 • 近似. 将每个小区间上的面积用 矩形的面积来近似。 • 积分和（黎曼和）. 将所有小矩 形面积求和，得到整体面积的 一个近似。 • 求极限. 让等分的份数趋近于无 穷大，所得极限就是所求面积 的精确值。
误差更小
定积分的定义
• 右图是正弦在一个周 期上的积分示意。为 20等分情形，取左端 点处的函数值
左端点型
定积分的定义
• 右图是正弦在一个周 期上的积分示意。为 20等分情形，取右的定义
• 右图是正弦在一个周 期上积分梯形公式的 示意。为8个分点情形。
梯形公式
定积分的定义
• 右图是正弦在一个周 期上积分梯形公式的 示意。为15个分点情 形。 • 可以看到，梯形公式 比矩形公式精确度高。
梯形，15个分点
分割 近似
求和
取极限
定积分的定义
• 现在看看分成40份的 情形。 • 可以看到误差变小了。 • 有理由相信：随着分 点的增加，误差越来 越小。
误差很小
定积分的定义
• 当然，小区间上的面 积也可以用其他容易 求出面积的图形的面 积来表示，比如梯形。 • 这就是定积分的梯形 算法。 • 右图是取5等分的情形， 就已经非常精确了。

第3-1章- 定积分的概念

第3-1章- 定积分的概念

1 ⎛ 1 ⎞⎛ 1⎞ = lim ⎜1 + ⎟⎜ 2 + ⎟ n ⎠⎝ n⎠ n→∞6 ⎝ Nhomakorabeao
1 = 3
i n
1x
例2. 用定积分表示下列极限:
i 1 (1) lim ∑ 1 + n →∞ n i =1 n
n
1 + 2 +L+ n (2) lim n →∞ n p +1 Δx i
p
p
p
n n i 1 解: (1) lim ∑ 1 + = lim ∑ 1 + i ⋅ 1 n →∞ n i =1 n n→∞ i =1 n n
o a
x1
L x i −1 ξ ix i L b x
( Δx
i
= xi − xi −1 , i = 1, 2, L , n
)
3) 近似和(求和)
A = ∑ ΔA i ≈ ∑ f (ξ i ) ⋅ Δx i
i =1 i =1
n
n
4) 取极限 令
λ = max{Δxi },
1≤ i ≤ n
n
则曲边梯形面积
b
∫
a
f ( x)dx = −
∫
a
b
f ( x)dx
∫
a
a
f ( x)dx = 0
定积分的几何意义:
f ( x) > 0 , f ( x) < 0 ,
∫ a f ( x ) dx = A ∫a
y
b
b
曲边梯形面积
f ( x) dx = − A 曲边梯形面积的负值
A1 a
b
A3 A2 A4
A5
b x

高中数学 定积分定义

高中数学 定积分定义
上页 下页 返回 退出
二、定积分定义
定积分的定义
lim a f (x)dx = 0 f (xi )Dxi
b i=1 n
.
b
根据定积分的定义, 曲边梯形的面积为 A = a f (x)dx . 变速直线运动的路程为 S = T v(t)dt .
1
T2
说明： 定积分的值只与被积函数及积分区间有关, 而与积分变 量的记法无关, 即
定积分概念与性质
一、定积分问题举例 二、定积分定义
三、定积分的性质
上页
下页
返回
退出
一、定积分问题举例
1.曲边梯形的面积
•曲边梯形 设函数y=f(x)在区间[a, b]上非负、连续. 由直线x=a、x=b、 y=0及曲线y=f (x)所围成的图形称为曲边梯形, 其中曲线弧称 为曲边.
上页
下页
返回
退出
这是因为g(x)f(x)0, 从而
b
b
a g (x)dx a f (x)dx = a[g (x) f (x)]dx 0 ,
所以
b
b
b
a f (x)dx a g(x)dx .
b
b
上页
下页
返回
退出
•性质5 如果在区间[a, b]上 f (x)0, 则
a f (x)dx 0 (a<b).
上页 下页 返回 退出
•定积分的几何意义 当f(x)0时, f(x)在[a, b]上的定积分表示由曲线y=f(x)、直 线x=a、x=b与x轴所围成的曲边梯形的面积.
当f(x)0时, f(x)在[a, b]上的定积分表示曲边梯形面积的 负值.
这是因为
lim lim a f (x)dx = 0 f (xi )Dxi = 0 [ f (xi )]Dxi = a [ f (x)]dx .

定积分的定义

定积分的定义
y
如何求出 A 的精确值？
o a x1
b xi1 xi xn1
x
i
（4）取极限
令 maxx1, x2,, xn
曲边梯形面积为
n
A lim f 0 i1
i
xi
y
o a x1
b xi1 xi xn1
x
整体等于部分之和
二. 定积分的概念
定义 设函数 f (x) 在 [a,b] 上有定义且有界，
在 a,b 任意插入 n 1 个分点 a x0 x1 xi1 xi
xn1 xn b , 将a,b分成n个小区间xi1, xi
i 1, 2, , n，用 xi xi xi1 i 1, 2, , n表示每个
小区间的长度,在每个小区间上任取一点 i xi1 , xi .
被 积 函 数
n
dx lim
被 0 i1 积积 表分 达变 式量
f
i xi
[a,b] 积分区间
注意：
（1）ab f xdx是一个常数.
（2）ab f xdx 只与 a,b 和 f x有关，而与区间
的分法和点 i 的取法以及积分变量用什么字母
表示无关.
b
n
作积的和式 f i xi. i 1
n
记

maxx1,
x2
,,
xn，若极限
lim
0
i 1
f
i xi
存在,则称此极限值为函数 f ( x)在区间[a, b]上的定积分，
记为
b
a
f

xdx，即
积分上限
积分下限
b a

定积分的概念

定积分的概念
a a
b
特别地： 若f x 在[a , b]上连续, f x 0, 且f x 不恒为零， 则 f 0.
a
例 比较积分值 e dx和 e x dx的大小.
x 0 0
1
1
解 因为当x [0,1]时，x x , 所以e x e
x
,

1
0
e dx e x dx.
2

sinxd x0
(2)
2

1
1
x dx 2 x 2dx
2 0
a a
a
1
f ( x )在 a, a 上连续且为奇函数时， f ( x)dx 0.
f ( x )在 a , a 上连续且为偶函数时， f ( x )dx 2 f ( x )dx
0 a a
性质5 （保向性） 若f x , g x 在a , b上均可积, 且恒有 f x g x , x a , b , 则 f

b
a
f x轴上方图形总面积 x轴下方图形总面积
b 1 a 0
例1.由几何意义求 dx, 其中b a;
2 2
1 x 2 dx.
key 1 ） 矩形面积： b a； 2 ） 单位圆x y 1的1 / 4面积： 4
例2 根据定积分几何意义， 说明下列各式成立 .

(1)

b
(i ) f ( x ) g( x ) 在[a, b]上可积，并且
(i i ) f ( x ) g( x )在a, b上也可积，但一般地
[ f ( x) g( x)]dx
a
a
f ( x )dx g( x )dx
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

b
a
f
(x)dx
abg(x)dx
.
上页 下页 返回 退出
•性质5 如果在区间[a, b]上 f (x)0, 则
b
a
f
(x)dx
0
(a<b).
•推论1 如果在区间[a, b]上 f (x)g(x), 则
b
a
f
(x)dx
abg(x)dx
(a<b).
•推论2
|
b
a
f
(x)dx|
ab|
f
(x)|
dx
(a<b).
01(1
x)dx
1 11 2
1 2
.
首页
上页 下页 返回 退出
三、定积分的性质
❖两点规定
(1)当 ab 时,
b
a
f
(x)dx
0
;
(2)当 ab 时,
b
a
f
(x)dx ba
f
(x)dx
.
上页 下页 返回 退出
三、定积分的性质
性 •性质质11
ab[
f
(x)
g(x)]dx
b
a
f
(x)dx
abg(x)dx
线xa、xb与x轴所围成的曲边梯形的面积.
当f(x)0时, f(x)在[a, b]上的定积分表示曲边梯形面积的
负值.
这是因为
b
a
f
n
(x)dx lim 0 i1
f
n
(xi
)Dxi
lim
0
[
i1
f
(xi )]Dxi
ab[
f
(x)]dx
.
上页 下页 返回 退出
•定积分的几何意义 当f(x)0时, f(x)在[a, b]上的定积分表示由曲线yf(x)、直
.
上页 下页 返回 退出
总结
１．定积分的实质：特殊和式的极限． ２．定积分的思想和方法：
分割 求和 取极限
化整为零
求近似以直（不变）代曲（变）
积零为整
取极限
精确值——定积分
上页 下页 返回 退出
小结 １．定积分的性质
（注意估值性质、积分中值定理的应用）
２．典型问题
（１）估计积分值； （２）不计算定积分比较积分大小．
•性质5 如果在区间[a, b]上 f (x)0, 则
b
a
f
(x)dx
0
(a<b).
•推论1 如果在区间[a, b]上 f (x)g(x), 则
b
a
f
(x)dx
abg(x)dx
(a<b).
这是因为g(x)f(x)0, 从而
所以
abg(x)dxab f (x)dx ab[g(x) f (x)]dx 0 ,
abg(x)dx
.
上页 下页 返回 退出
三、定积分的性质
性 •性质质11
ab[
f
(x)
g(x)]dx
b
a
f
(x)dx
abg(x)dx
.
性 •性质质22
abkf
(x)dx
k
b
a
f
(x)dx
.
>>>
性 •性质质33
b
a
f
(x)dx
c
a
f
(x)dx
b
c
fห้องสมุดไป่ตู้
(x)dx
.
>>>
注：值得注意的是不论a, b, c的相对位置如何上式总成立.
n
(3)求和:
曲边梯形的面积近A 似li为m 0 i1
f
(xi )Dxi
;.
(4)取极限: 设max{Dx1, Dx2,, Dxn}, 曲边梯形的面积为
n
A
lim
0 i1
f
(xi )Dxi
.
上页 下页 返回 退出
2.变速直线运动的路程
已知物体直线运动的速度vv(t)是时间 t 的连续函数, 且
•观察与思考 在曲边梯形内摆满小的矩形, 当小矩形的宽度减少时,
小矩形面积之和与曲边梯形面积之间的误差将如何变化? 怎样求曲边梯形的面积？
上页 下页 返回 退出
•求曲边梯形的面积
(1)分割: ax0< x1< x2< < xn1< xn b, Dxixixi1;
(2)近似代替: 小曲边梯形的面积近似为f(xi)Dxi (xi1<xi<xi);
v(t)0, 计算物体在时间段[T1, T2]内所经过的路程S.
(1)分割: T1t0<t1<t2< <tn1<tnT2, Dtititi1;
(2)近似代替: 物体在时间段[ti1, ti]内所经过的路程近似为
DSiv(i)Dti ( ti1< i<ti );
(3)求和: 物体在时间段[T1, T2]内所经过的路程近似为
的定积分,
记为
b
a
f
(x)dx
,
即
b
a
f
(x)dx
n
lim
0 i1
f
(xi
)Dxi
.
上页 下页 返回 退出
二、定积分定义
❖定积分的定义
b
a
f
(x)dx
n
lim
0 i1
f
(xi
)Dxi
.
•定积分各部分的名称
————积分符号,
n
f
(xi )Dxi
———积分和.
f(x) ———被积函数, i1
f(x)dx ——被积表达式,
这是因为|f(x)|f(x)|f(x)|, 所以
ab|
f
(x)|dx
b
a
f
(x)dx
ab|
f
(x) | dx
,
即
|
b
a
f
(x)dx|
ab|
f
(x)|
dx
.
上页 下页 返回 退出
•性质5 如果在区间[a, b]上 f (x)0, 则
b
a
f
(x)dx
0
(a<b).
•推论1 如果在区间[a, b]上 f (x)g(x), 则
定积分概念与性质
一、定积分问题举例 二、定积分定义 三、定积分的性质
上页 下页 返回 退出
一、定积分问题举例
1.曲边梯形的面积
•曲边梯形 设函数yf(x)在区间[a, b]上非负、连续. 由直线xa、xb、
y0及曲线yf (x)所围成的图形称为曲边梯形, 其中曲线弧称 为曲边.
上页 下页 返回 退出
上页 下页 返回 退出
三、定积分的性质
性 •性质质11
ab[
f
(x)
g(x)]dx
b
a
f
(x)dx
abg(x)dx
.
性 •性质质22
abkf
(x)dx
k
b
a
f
(x)dx
.
性 •性质质33
b
a
f
(x)dx
c
a
f
(x)dx
b
c
f
(x)dx
.
性 •性质质44 ab1dx abdx ba .
上页 下页 返回 退出
n
S v( i )Dti ;
i1
(4)取极限: 记max{Dt1, Dt2,, Dtn}, 物体所经过的路程为
n
S
lim
0
i1
v(
i
)Dti
.
上页 下页 返回 退出
二、定积分定义
❖定积分的定义
设函数f(x)在区间[a, b]上有界.
•在区间[a, b]内插入分点: ax0<x1<x2< <xn1<xnb;
定积分的值只与被积函数及积分区间有关, 而与积分变
量的记法无关, 即
b
a
f
(x)dx
b
a
f
(t)dt
b
a
f
(u)du
.
上页 下页 返回 退出
二、定积分定义
❖定积分的定义
❖函数的可积性
b
a
f
(x)dx
n
lim
0 i1
f
(xi
)Dxi
.
如果函数f(x)在区间[a, b]上的定积分存在, 则称f(x)在区
解:
取分点为
Dxi
1 n
(i1,
2,
,
n1),
则
xi
i n
(i1,
2,
,
n).
在第i
个小区间上取右端点 x i
xi
i n
(i1,
2,
,
n).
于是
1e xdx lim
n
i
en
1
lim
1
(e
1 n
e
2 n
e
n n
)
0
n i1 n n n
1
1
1
lim
1 e n [1(e n
)n ] lim
e n [1e]
上页 下页 返回 退出
间[a, b]上可积. •定理1
如果函数f(x)在区间[a, b]上连续, 则函数f(x)在区间[a, b]
上可积.
•定理2
如果函数f(x)在区间[a, b]上有界, 且只有有限个间断点,