a16 19.4 课题学习 重心学案(二)
- 格式:doc
- 大小:100.00 KB
- 文档页数:5

查汗淖尔学校师生共用教学案48年级:八年级科目:数学执笔:审核:课题:19.4重心课时:2 课型:新授备课时间:2012.4.21 授课时间:教学目标:1.通过课题学习的任务、目的、过程、结论等环节,培养学生的探究能力和创新意识(重点)2.数学活动的规范操作,以及寻找线段、平行四边形的重心(难点)学法指导:“读·议·展·点·练”教学过程:(一)自主学习(不比聪明比勤奋,不比基础比进步)1.请同学们准备一根均匀的木条或其他形状是线段的物体,找出其平衡点,并做出标记。
2.请同学们准备一个平行四边形形状的物体,找出平衡点,并做出标记。
3.重心的物理意义:在一块均匀的木板上,我们可以找到一点,如果用手指顶住这一点,木板会保持,这个平衡点就是这块木板的。
(二)合作探究(你说我讲,快乐课堂,你争我抢,放飞梦想)1.探究线段的重心实验步骤:(1)找出平衡点的位置如图所示,两手分开,把均匀木条水平架在左右手的食指上,把两食指相对交替靠拢,直到并在一起为止。
用一个食指支在此处,木条能呈水平平衡。
(2)用刻度尺量出平衡点的位置。
(3)再用另一根木条寻找平衡点。
(4)你能说出木条的重心在什么位置吗?(5)根据上面的活动,你有什么发现?我的发现:2.探究平行四边形的重心实验步骤:(1)用一个手指顶住一块均匀的正方形硬纸片,找出平衡点的位置。
(2)探索这个平衡点与正方形对角线的交点有什么关系?(3)根据(2)的发现,你能得出矩形、菱形、一般平行四边形的重心在什么位置?我的发现:(三)本节收获:(四)课后检测(不为失败找理由,只为成功想办法)1.线段的重心是线段的2.平行四边形、矩形、菱形、正方形的重心都是3.走钢丝的杂技演员要使自己更稳一些,他们都是( )A 使重心低一些B 使重心高一些C 走得快一点D 高高举起手中的铁棒4. 画出下面图形的重心O.教(学)反思:。
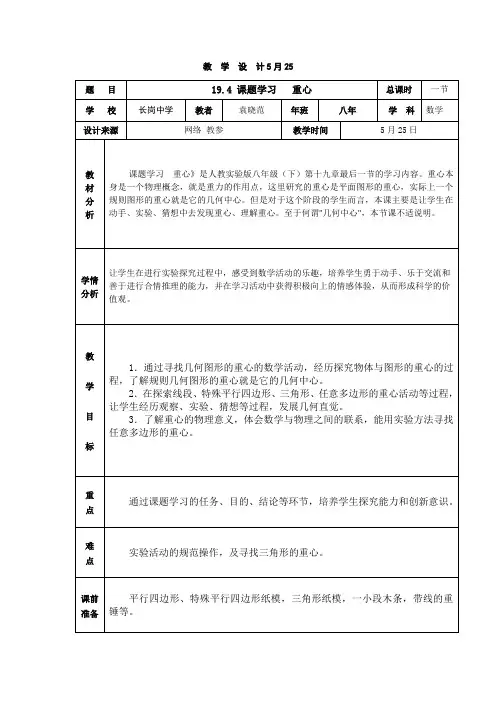

三角形重心的解题思路分析
[解题过程]
三条中线才具有性质:三条中线的交点(重心,一定在三角形内)把三条中线都分成2:1的两段.
三条高的交点(垂心)则不同,它可以在三角形内、可以在三角形的边上、也可以在三角形的外部,所以,不存在分高线为定比的情况.
证明:设△ABC中BE、CF是AC、AB边上的中线,连接E、F.
则EF∥BC并且EF=BC/2.
设BE∩CF=M,∵EF∥BC.∴△AEF∽△ABC △BMC∽△EMF并且BC:CF=2:1,因此CM:MF=BM:ME=2:1.
连接AM,与EF交于H,与BC交于D.根据平行截割定理得知△MHF∽△MDC,并且CD:HF=2:1.因此D是BC的中点,因而AD是边BC上的中线,并且经过点M.
所以三角形的三条中线交于一点M,并且此点分中线的比是2:1.
1。



八年级数学下册 19.4重心导学案人教新课标版19、4 重心导学案【学习目标】通过寻找图形重心的过程,掌握常见几何图形的重心,体会数学与物理的联系、【重难点】三角形的重心及其应用、【学习过程】1、课前自学:(1)给你一块质地均匀的木板,你能迅速地找出它的重心吗?(2)对于常见的几个图形(如:线段、三角形、平行四边形、矩形、梯形……),你知道它们的重心在哪儿吗?(3)任意多边形都可以用法迅速找出它的重心、2、展示交流:(1)重心就是、(2)常见几个图形的重心:线段的重心是;平行四边形的重心是;矩形、菱形、正方形呢?梯形的重心是对角线的交点吗?等腰梯形呢?(3)三角形的重心在哪儿?(4)几何图形的重心一定在形内吗?3、合作探究例1、在△ABC中,BD、CE是边AC、AB上的中线,BD与CE相交于点O、①BO与OD的长度有什么关系?②BC边上的中线是否一定过点O?为什么?例2、如图,在△ABC中,AB=AC,G是△ABC的重心,过G点作GD⊥AB, GE ⊥AC,垂足为D,E、(1)猜想:GD_______GE;(2)试对上面的猜想加以证明、例3、如图,一个“L”形的图形,请你用一条直线将它分割成面积相等的两部分、4、拓展反馈:(1)寻找重心常用的两种方法是:和、(2)线段的重心就是线段的_______;平行四边形、矩形、菱形、正方形的重心都在____ ____;(3)三角形的重心是,•三角形的重心到顶点的距离等于对边中点的距离的_____、(4)如图1所示,△ABC,D、E、F三点将BC四等分,AG:AC=1:3,H为AB的中点,•下列哪一个点为△ABC的重心()A、XB、YC、ZD、W (1)(2)(3)(5)如图2所示,四边形ABCD为一正方形,E、F分别为BC、CD的中点,•对角线AC与BD相交于O点,且AE与OB相交于G点,AF与OD相交于H点,下列说法正确的有()①E点是线段BC的重心; ②G点是△ABC的重心; ③H点是△ADC的重心;④O点是正方形ABCD的重心、A、1个B、2个C、3个D、4个(6)如图3所示,已知G为直角△ABC的重心,∠ABC=90,且AB=12cm,BC=9cm,则△AGD的面积是()A、9cm2B、12cm2C、18cm2D、20cm2(7)已知△ABC,请你画出它的重心O、(8)如图,ABCD中,E、F分别是BC、CD的中点, AE、AF分别交BD于M、N,•求证:BM=MN=ND、【学习小结】XXXXX:1、找重心常用的两种方法是什么?2、常见几个图形的重心在哪儿?3、对于三角形的重心,你掌握了哪些?。

19.4 课题学习重心(二)
牛庄镇西范中学燕爱玲禹振东
三维学习目标
一、知识与技能
1.进一步认识规则几何图形的重心就是它的几何中心.
2.探究不规则几何图形的重心.
二、过程与方法
1.通过悬挂法探究三角形的重心.
2.讨论特殊三角形的重心.
3.进一步探究任意多边行的重心.
三、情感态度与价值观
在进行探索的活动中培养学生合作交流的意识与合情的推理能力.
教学重点:用悬挂法探究不规则几何图形的重心.重点是让学生在动手操作的同时,认真思考.
教学难点:用悬挂法探究不规则几何图形的重心的过程.
教学过程
一、创设问题情境,搭建研究平台
(1)线段的重心是线段的中点.
(2)平行四边形的重心,是它的两条对角线的交点.
二、分组讨论探究新知
三角形的重心.
活动过程:
先分组,
1,活动与探究
如果我们身旁没有量角器或三角尺,又需要做60°、30°、15°等大小的角,可以采用下面的
方法(如下图).
(1)对折矩形纸片ABCD,使AD与BC重和,得到折痕EF,把纸片展平.
(2)再一次折叠纸片,使点A落在EF上,并使折痕过点B,得到折痕BM,同时得到了线段BN.
观察所得的∠ABM、∠MBN和∠NBC,在三个角有什么关系?你能证明吗?
通过证明可知,简单而准确.由此,15°、60°、120°、150°等角,就都容易得到了.
已知:矩形ABCD,E、F分别为边AB、CD的中点,N在EF上,且MN=AM,(如图),BN=AB.
求;∠ABM、∠MBN和∠NBC的大小
解:如右图延长MN交BC于点P
∵AM=MN,AB=NB,BM=BM,
∴△ABM≌△NBM(SSS)∴∠ABM=∠MBN.
又∵EF 为矩形ABCD 的中位线,
∴MN=NP.
又∵BN=BN,∠BNM=∠BNP=Rt ∠.
∴△BMN ≌△BPN.
∴∠MBN=∠NBP.
∴∠ABM=∠MBN=∠NBP=30°.
2,形ABCD 的周长为40cm ,上底CD=7cm,DE ∥BC,G 、F 分别为AD 、AE 中点,且GF=0.5BC ,求△AED 与△AFG 的周长。
三、学以致用,拓展思维
求:1.点G 到直角顶点C 的距离GC ;
2.点G 到斜边AB 的距离
四、课时小结,抽取规律。
前一节课的探索基础上,我们进一步对、任意多边形等一些不规则几何图形的重心进行了探究.在实际操作过程中,同学们充分发挥自己的主动性,积极思考、大胆设想,体现了我们探究性学习的主旨,可以说,我们在这节课中收获是很大的.
课堂达标检
1、阅读填空题
阅读下面命题的证明过程后填空:
已知:如图BE 、CF 是ΔABC 的中线,BE 、CF 相交于G 。
求证:
2
1==GC GF GB GE 证明:连结EF
∵E 、F 分别是AC 、AB 的中点
∴EF ∥BF 且EF =2
1BC ∴2
1===BC EF GC GF GB GE 问题:
(1)连结AG 并延长AG 交BC 于H ,点H 是否为BC 中点 (填“是”或“不是”)
(2)①如果M 、N 分别是GB 、GC 的中点,则四边形EFMN 是 四边形。
的长。
求:相交于点中线与
中已知:BC cm GE cm AD G BE AD BC AD AC AB ABC ,5,18;,,==⊥=∆;,3,4,90,的重心是已知:ABC G BC AC ACB ACB Rt o ∆===∠
∆
②当
AC
AB 的值为 时,四边形EFMN 是矩形。
③当BC
AH 的值为 时,四边形EFMN 是菱形。
④如果AB =AC ,且AB =10,BC =16,则四边形EFMN 的面积S = 。
G
N M
H F
E C B A
2、在△ABC 中,借助作图工具可以作出中位线EF ,沿着中位线EF 一刀剪切后,用得到的△AEF 和四边形EBCF 可以拼成平行四边形EBCP ,剪切线与拼图如图示1,仿上述的方法,按要求完成下列操作设计,并在规定位置画出图示,
⑴在△ABC 中,增加条件_____,沿着_____一刀剪切后可以拼成矩形,剪切线与拼图画在图示2的位置;
⑵在△ABC 中,增加条件______,沿着_____一刀剪切后可以拼成菱形,剪切线与拼图画在图示3的位置;
⑶在△ABC 中,增加条件_______,沿着_____一刀剪切后可以拼成正方形,剪
切线与拼图画在图示4的位置
⑷在△ABC (AB ≠AC )中,一刀剪切后也可以拼成等腰梯形,首先要确定剪切线,其操作过程(剪切线的作法)是:_______________
________________________________
________________________ 然后,沿着剪切线一刀剪切后可以拼成等腰梯形,剪切线与拼图画在图
示5的位置.
A B C P F E (E ) (A )
课堂达标检答案
1、(1)是;(2)①平行;②1;③
2
3;④16。
2、⑴ 方法一:∠B =90°,中位线EF ,如图示2-1.
方法二:AB =AC ,中线(或高)AD ,如图示2-2.
⑵ AB =2BC (或者∠C =90°,∠A =30°),中位线EF ,如图示3.
⑶ 方法一:∠B =90°且AB =2BC ,中位线EF ,如图示4-1.
方法二:AB =AC 且∠BAC =90°,中线(或高)AD ,如图示4-2.
⑷ 方法一:不妨设∠B >∠C ,在BC 边上取一点D ,作∠GDB =∠B 交AB 于G ,过AC 的中点E 作EF ∥GD 交BC 于F ,则EF 为剪切线.如图示5-1.
方法二:不妨设∠B >∠C ,分别取AB 、AC 的中点D 、E ,过D 、E 作BC 的垂线,G 、H 为垂足,在HC 上截取HF =GB ,连结EF ,则EF 为剪切线.如图示5-2.
方法三:不妨设∠B >∠C ,作高AD ,在DC 上截取DG =DB ,连结AG ,过AC 的中点E 作EF ∥AG 交BC 于F ,则EF 为剪切线.如图示5-2. 图示1 A
B
C P F E (E )
(A ) 图示2 图示3
图示4 图示5
图示2-1
(C)
图示2-2 图示4-1 图示4-2 图示5-1
图示3
图示5-2 图示5-3
A
A
B
E
F
C (A)
P (E)
H
B D
C (A)
P (D) A
B
C (A)
P (E)
F
E
A
B
C (A)
P (E)
F
E
C (A)
)
A
B
D
G
E
P (F)(C)
A
B
D
G
E
F C
P (F)(C)
A
B
D G
E
F C
P (F)。