面的投影
- 格式:doc
- 大小:44.50 KB
- 文档页数:5

2-2 点、线、面的投影特性一、点的投影1、点的三面投影点是组成物体最基本的几何元素。
如图2-9所示,在三投影面体系中,由空间点A(x,y,z)分别向三投影面作正投影,得其三面投影a(x,y)、a′(x,z)、a″(y,z),即过点A分别作三投影面的垂线,其垂足即为点A的三面投影;展开H面和W面,得到点A的三视图:a 、a′长对正,a′、a″高平齐,a 、a″宽相等,如图2-10所示。
图2-9 点的三面投影图2-10 点的三视图例1 :已知空间点B的两面投影b ,b′,如图2-11所示,求其第三面投影b″。
分析:空间点B的三面投影b 、b′、b″符合“长对正,高平齐,宽相等”的投影规律。
作图: b′与b″高平齐,b与b″宽相等,则其交点即为b″。
图2-11 求点的第三面投影图2-12 求点的三面投影例2 :已知空间点D(5,4,3),如图2-12所示,求其三面投影。
分析:空间点D的三面投影分别为d(x,y)、d′(x,z)、d″(y,z),且符合“长对正,高平齐,宽相等”的投影规律。
作图:分别在三投影轴上取x1=5,y1=4,z1=3,按“长对正,高平齐,宽相等”的投影规律分别作直线段,交点即为空间点D的三面投影(d 、d′、d″)。
2、两点的相对位置空间两点的相对位置是指空间两点间前后、左右、上下的位置关系。
两点在空间的相对位置可以根据两点的坐标值来判定,如图2-13所示。
X坐标确定两点的左右位置关系。
X坐标值大的点在左;Y坐标确定两点的前后位置关系。
Y坐标值大的点在前;Z坐标确定两点的上下位置关系。
Z坐标值大的点在上。
图2-13 两点的相对位置故A点在B点的右,后,上方,即B点在A点的左,前,下方。
3、重影点及其可见性判断若空间两点在某一投影面上的投影重合,则称这两点为该投影面的重影点。
此时,这两点位于同一投射线上,且有两个坐标的值分别相等,不等值的坐标之大小可以确定重影点的可见性,即X、Y、Z坐标值大的点分别位于左方、前方、上方,为可见点,如图2-14所示。


立体几何——面的投影专题面的投影是立体几何中的重要概念,它是指一个面在特定方向上的影子或投影。
在这篇文档中,我们将介绍面的投影的基本原理和计算方法。
1.面的投影类型面的投影可以分为正投影和斜投影两种类型。
1.1 正投影正投影是指面在一个垂直于面的方向上的投影。
这种投影形成的影子与原始面的形状完全相同,只是大小不同。
我们可以通过平行投影的方法来计算正投影。
1.2 斜投影斜投影是指面在一个斜向方向上的投影。
相比于正投影,斜投影的影子与原始面的形状有所变形。
斜投影的计算方法复杂一些,需要考虑投影线与面的夹角和投影方向。
2.计算方法计算面的投影需要使用一些几何知识和公式。
以下是面的投影计算的基本步骤:2.1 正投影计算正投影的计算方法相对简单,主要包括以下几个步骤:确定投影线的方向和长度。
将投影线与面的交点连接起来,得到投影图形。
计算投影图形的面积。
2.2 斜投影计算斜投影的计算稍微复杂一些,具体步骤如下:确定投影线的方向和长度。
根据投影线的夹角和面的法向量,计算投影线在面上的投影长度。
将投影线在面上的投影长度与投影线的方向连接起来,得到投影图形。
计算投影图形的面积。
3.应用实例面的投影在生活和工程中有广泛的应用。
下面是一些面的投影的实际应用实例:在建筑设计中,通过计算建筑物在不同方向上的投影面积,可以评估光照和遮挡效果,为室内外设计提供参考。
在图形学和计算机图像处理中,通过计算面的投影,可以实现三维场景的二维显示,从而实现虚拟现实和增强现实技术。
在制造业中,通过计算物体在机械加工过程中的投影面积,可以评估切割和排布方案,提高生产效率。
4.总结面的投影是立体几何中的重要概念,通过计算面在特定方向上的投影,我们可以得到有关形状、遮挡和光照的信息。
正投影和斜投影都是常见的投影方式,计算方法略有差异。
面的投影在建筑设计、图形学和制造业等领域有广泛应用。
注:该文档的内容来源于立体几何和几何投影的基本原理,确保准确性,但不引用任何无法确认的内容。


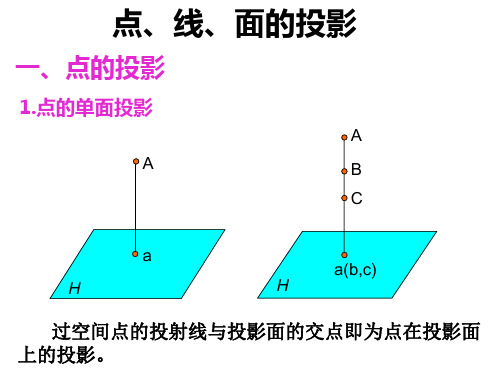
空间点对于由V、H和W面组成的投影体系有三种位置关系:(1)当点的x、y、z坐标均不为零时,点的三面投影均落在投影面内;(2)当点的x、y、z坐标有一个为零时,空间点在投影面上,其两个投影落在投影轴上,特别值得注意的是,当点在H面上时,其W面的投影落在Y 轴上,当按三视图的形成方法展开投影体系时,其W面投影随Y轴一起绕Z轴向后旋转落在YW 轴上。
(3)当点的x、y、z坐标均有两个为零时,空间点在投影轴上,其一个投影与原点重合。
点的三面投影规律⑴ 点的正面投影和水平投影的连线垂直于OX轴。
⑵ 点的正面投影和侧面投影的连线垂直于OZ轴。
⑶ 点的水平投影到OX轴的距离等于侧面投影到OZ轴的距离。
[投影面垂直线]空间直线对投影面有三种位置关系:平行、垂直和倾斜。
若空间直线垂直于一个投影面,则必平行于其他两个投影面,这样的直线称之为投影面垂直线,对于垂直于V、H、W面的直线分别称之为正垂线、铅垂线和侧垂线。
投影面垂直线在其垂直的投影面上的投影积聚为一个点,其他两个投影面上投影平行(或垂直)于投影轴,且反映实长。
若空间直线平行于一个投影面,倾斜于其他两个投影面,这样的直线称之为投影面平行线,按其平行于V、H、W面分别称之为正平线、水平线和侧平线。
投影面平行线在其平行的投影面上的投影反映实长,其他两个投影面上投影平行(或垂直)于投影轴,且投影线段的长小于空间线段的实长。
一般位置直线和三个投影面均处于倾斜位置,其三个投影和投影轴倾斜,且投影线段的长小于空间线段的实长。
从投影图上也不能直接反映出空间直线和投影平面的夹角。
[投影面平行面]空间平面对投影面有三种位置关系:平行、垂直和一般位置。
若空间平面平行于一个投影面,则必垂直于其他两个投影面,这样的平面称之为投影面平行,对平行于V、H、W面的平面分别称之为正平面、水平面和侧平面。
投影面平行面在其平行的投影面上的投影反映实形,其他两个投影面上投影积聚成一条直线,且垂直于该投影面内的投影轴[投影面垂直面]若空间平面垂直于一个投影面,而倾斜于其他两个投影面,这样的平面称之为投影面垂直面,按垂直于V、H、W面的平面分别称之为正垂面、铅垂面和侧垂面。
第二章投影的基本知识和点、线、面的投影基本要求:建立投影的概念,掌握正投影的基本性质;掌握点线面的投影特性;根据投影能判断出点、线、面的关系。
主要内容:1、投影的基本知识;2、点的投影;3、直线的投影;4、平面的投影。
2.1 投影的基本知识一、内容:1、投影的基本概念;2、投影的类型;3、工程中常用的投影图。
二、要求及重点:要求掌握投影的基本概念;了解投影的类型、用途。
三、教学方式:通过实物及日常生活中的现象,使学生掌握投影的基本概念;了解投影的类型、用途。
2.1 投影的基本知识一、投影的概念1、在日常生活中,经常看到空间一个物体在光线照射下在某一平面产生影子的现象,抽象后的“影子”称为投影。
2、产生投影的光源称为投影中心S,接受投影的面称为投影面,连接投影中心和形体上的点的直线称为投影线。
形成投影线的方法称为投影法(图2-1)。
(a) (b)图2-1 中心投影法图2-2 平行投影法二、投影的类型投影法分为中心投影法和平行投影法两大类。
1、中心投影法光线由光源点发出,投射线成束线状。
投影的影子(图形)随光源的方向和距形体的距离而变化。
光源距形体越近,形体投影越大,它不反映形体的真实大小。
2、平行投影法光源在无限远处,投射线相互平行,投影大小与形体到光源的距离无关,如图2-2所示。
平行投影法又可根据投射线(方向)与投影面的方向(角度)分为斜投影(a)和正投影(b)两种。
(1)斜投影法:投射线相互平行,但与投影面倾斜,如图2-2(a)所示。
(2)正投影法:投射线相互平行且与投影面垂直,如图2-2(b)所示。
用正投影法得到的投影叫正投影。
三、工程上常用的投影图1、透视图用中心投影法将空间形体投射到单一投影面上得到的图形称为透视图,如图2-3。
透视图与人的视觉习惯相符,能体现近大远小的效果,所以形象逼真,具有丰富的立体感,但作图比较麻烦,且度量性差,常用于绘制建筑效果图。
图2-3 透视图图2-4 轴测图2、轴测图将空间形体正放用斜投影法画出的图或将空间形体斜放用正投影法画出的图称为轴测图。
《建筑制图》教案
面的投影
授课教师:张小龙授课班级:12建筑
土木工程制图电子教案
教学课题:
平面的投影
课程导入:(1)点构成线,线构成面,面构成体。
对点、线的投影的清楚的掌握是理解和掌握面的投影的前提。
理解和明白了面的投影才能
清晰明白的画出几何体的三面投影。
(2)三面投影反映的位置关系
教学目标:
(1)掌握平面表示的方法。
(2)理解和掌握投影面平行面的投影特性。
(3)理解和掌握投影面垂直面的投影特性。
(4)理解和掌握投影面一般位置平面的投影特性。
教学重点、难点:
重点:
(1)平面的表示方法。
(2)特殊位置平面的投影特性。
(3)根据投影特性判定平面位置。
难点:
(1)特殊位置平面的投影特性。
(2)根据投影特性判定位置平面。
教学方法:讲授法、演示法、练习法、归纳法。
教学内容及过程:
一、平面的表示方法
1)不在一条直线上的三点
2)一条直线和线外一点
3)两平行直线
4)两相交直线
5)任意一平面图形
二、平面的分类及定义
(1)特殊位置平面
1)投影面平行面:
平行于一个投影面也即同时垂直于其它两个投影面的平面,称为投影面平行面。
a)水平面(∥H面)
b)正平面(∥V面)
c)侧平面(∥W面)
2)投影面垂直面
仅垂直于一个投影面,而与另外两个投影面倾斜的平面,称为投影面垂直面。
a)铅锤面(⊥H面)
b) 正垂面(⊥V面)
c) 侧垂面(⊥W面)
(2)一般位置平面
对三个投影面都倾斜的平面,称为一般位置平面。
三、平面的投影特性
1、三种投影面平行面的投影特性:
(1)真实性——平面在其所平行的投影面上的投影,反映
平面的实形;
(2)积聚性——在另外两个投影面上的投影为直线段(有
积聚性)且平行于相应的投影轴;
2、投影面垂直面的投影特性:
(1)积聚性——在其所垂直的投影面上的投影为倾斜直线
段,该倾斜直线段与投影轴的夹角,反映该平面对相应投影
面的倾角;
(2)相仿性——若平面用平面形表示,则在另外两个投影
面上的投影仍为平面形,但不是实形;
3、一般位置平面的投影特性:
(1)类似性——在三个投影面上的投影均为相仿的平面图
形,且形状缩小;
四、根据投影面的投影特性判别平面位置
1、三种投影面平行面的投影特性:
判别——若在平面的投影中,同时有两个投影分别积聚成平
行于投影轴的直线,而只有一个投影为平面形,则此平面平
行于该投影所在的那个投影面。
该平面形投影反映该空间平
面形的实形。
2、投影面垂直面的投影特性:
判别——若平面形在某一投影面上的投影积聚成一条倾斜于
投影轴的直线段,则此平面垂直于积聚投影所在的投影面。
3、一般位置平面的投影特性:
判别——平面的三面投影都是类似的几何图形,该平面一定
是一般位置平面。
作业、小结:
小结:
(1)平面的表示方法有五种
(2)特殊位置平面的投影特性及判定
1)投影面平行面:a)“一框两直”且两直平行于投影轴;
b)在哪个投影面为框就与那个面的平行。
2)投影面垂直面:a)“两框一直”,框不反映实形;
b)哪个面为一直线就是那个面的垂直面。
3)一般位置平面:“三框”且不反映实形。
作业:
建筑制图习题集P16 1、2、3。