当前位置：文档之家 › 面的投影

面的投影

  • 格式：ppt
  • 大小：2.08 MB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

2-2 点、线、面的投影特性

2-2 点、线、面的投影特性

2-2 点、线、面的投影特性一、点的投影1、点的三面投影点是组成物体最基本的几何元素。

如图2-9所示，在三投影面体系中，由空间点A（x，y，z）分别向三投影面作正投影，得其三面投影a（x，y）、a′(x，z）、a″（y，z），即过点A分别作三投影面的垂线，其垂足即为点A的三面投影；展开H面和W面，得到点A的三视图：a 、a′长对正，a′、a″高平齐，a 、a″宽相等，如图2-10所示。

图2-9 点的三面投影图2-10 点的三视图例1 ：已知空间点B的两面投影b ，b′，如图2-11所示，求其第三面投影b″。

分析：空间点B的三面投影b 、b′、b″符合“长对正，高平齐，宽相等”的投影规律。

作图： b′与b″高平齐，b与b″宽相等，则其交点即为b″。

图2-11 求点的第三面投影图2-12 求点的三面投影例2 ：已知空间点D(5,4,3)，如图2-12所示,求其三面投影。

分析：空间点D的三面投影分别为d（x，y）、d′（x，z）、d″（y，z），且符合“长对正，高平齐，宽相等”的投影规律。

作图：分别在三投影轴上取x1=5，y1=4，z1=3，按“长对正，高平齐，宽相等”的投影规律分别作直线段，交点即为空间点D的三面投影（d 、d′、d″）。

2、两点的相对位置空间两点的相对位置是指空间两点间前后、左右、上下的位置关系。

两点在空间的相对位置可以根据两点的坐标值来判定，如图2-13所示。

X坐标确定两点的左右位置关系。

X坐标值大的点在左；Y坐标确定两点的前后位置关系。

Y坐标值大的点在前；Z坐标确定两点的上下位置关系。

Z坐标值大的点在上。

图2-13 两点的相对位置故A点在B点的右，后，上方，即B点在A点的左，前，下方。

3、重影点及其可见性判断若空间两点在某一投影面上的投影重合，则称这两点为该投影面的重影点。

此时，这两点位于同一投射线上，且有两个坐标的值分别相等，不等值的坐标之大小可以确定重影点的可见性，即X、Y、Z坐标值大的点分别位于左方、前方、上方，为可见点，如图2-14所示。

立体几何——面的投影专题

立体几何——面的投影专题

立体几何——面的投影专题面的投影是立体几何中的重要概念，它是指一个面在特定方向上的影子或投影。

在这篇文档中，我们将介绍面的投影的基本原理和计算方法。

1.面的投影类型面的投影可以分为正投影和斜投影两种类型。

1.1 正投影正投影是指面在一个垂直于面的方向上的投影。

这种投影形成的影子与原始面的形状完全相同，只是大小不同。

我们可以通过平行投影的方法来计算正投影。

1.2 斜投影斜投影是指面在一个斜向方向上的投影。

相比于正投影，斜投影的影子与原始面的形状有所变形。

斜投影的计算方法复杂一些，需要考虑投影线与面的夹角和投影方向。

2.计算方法计算面的投影需要使用一些几何知识和公式。

以下是面的投影计算的基本步骤：2.1 正投影计算正投影的计算方法相对简单，主要包括以下几个步骤：确定投影线的方向和长度。

将投影线与面的交点连接起来，得到投影图形。

计算投影图形的面积。

2.2 斜投影计算斜投影的计算稍微复杂一些，具体步骤如下：确定投影线的方向和长度。

根据投影线的夹角和面的法向量，计算投影线在面上的投影长度。

将投影线在面上的投影长度与投影线的方向连接起来，得到投影图形。

计算投影图形的面积。

3.应用实例面的投影在生活和工程中有广泛的应用。

下面是一些面的投影的实际应用实例：在建筑设计中，通过计算建筑物在不同方向上的投影面积，可以评估光照和遮挡效果，为室内外设计提供参考。

在图形学和计算机图像处理中，通过计算面的投影，可以实现三维场景的二维显示，从而实现虚拟现实和增强现实技术。

在制造业中，通过计算物体在机械加工过程中的投影面积，可以评估切割和排布方案，提高生产效率。

4.总结面的投影是立体几何中的重要概念，通过计算面在特定方向上的投影，我们可以得到有关形状、遮挡和光照的信息。

正投影和斜投影都是常见的投影方式，计算方法略有差异。

面的投影在建筑设计、图形学和制造业等领域有广泛应用。

注：该文档的内容来源于立体几何和几何投影的基本原理，确保准确性，但不引用任何无法确认的内容。

6-平面的投影

6-平面的投影
CD平行于属于平面P的 直线AB，
则CD与平面P平行。
例6-4 已知直线DE∥△ABC，试完成直线DE的水平投影。
解：因为直线DE∥△ABC，所以在△ABC中必可找到 一条直线与DE平行。该直线的投影也必然与DE的同 面投影平行。
例6-5 试判别直线DE是否平行于△ABC。
解：如果在△ABC所确定的平面内能找到平行于直线DE的 直线，则直线DE∥△ABC，否则直线DE与△ABC不平行。
例6-2 已知ΔABC内一点K的水平投影k，求其正面投影k’。
解法2：运用点在平面上的条件求k’。
(1) 在平面的水平投影△ abc上，连ak与bc相交于点3； (2) 由点3作垂线与b’c’相交于点3’； (3) 连a’3’与过k所作的垂线交于k’。
直线在平面上的条件是：
若一直线通过平面上任意两 已知点，则直线在该平面上。
线AC、AD、AE等，这些直
线对投影面H的倾角各不相
同，但其中必有一条直线
AD对投影面的倾角是最大
的，该直线垂直于直线CE，
即垂直于平面P关于投影面
H的平行线，此直线称为平 面P对投影面H的最大斜度 在三投影面体系中对H、V、W面分别
线。
有三组不同的最大斜度线。最大斜度
线对投影面的倾角反映平面对该投影
n
f
c
a
m b
d
a d
f
m
c
b n
例6-14 平面由两平行线AB、CD给定，试判断直线MN
是否垂直于定平面。
a
c
m
e
f
b
d
X
n
O
b
a
m
e
d
c
n
f

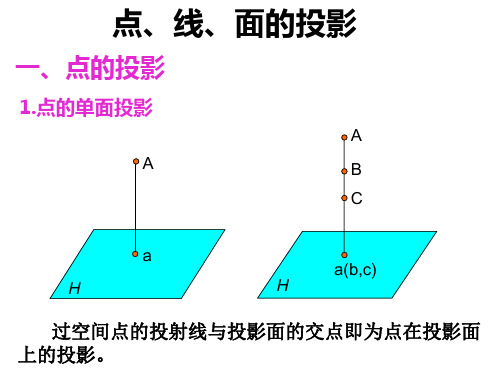
点、线、面的投影

点、线、面的投影
a
投影特性：
H
c
1、abc、abc分别积聚为一条直线，且平行相应的投影轴； 2、水平投影abc反映 ABC实形。
正平面
V
b a B A C c a b W a c H b c b a c b
b a a
c
c
投影特性：
1、abc、abc分别积聚为一条直线，且平行相应的投影轴；
（2）两直线相交的判断 ①各同面投影都相交 ②若为一般位置线， 有两组同面投影相交 ③有某一投影面的平 行线时 且交点符 合点的投 影规律 相交
例1.12
c
须验证两直线在该投影面上的投 影是否相交，或用定比性作图判 断交点是否符合交点规律。 如图所示，直线AB和CD相交，求作cd 。
b
a
b′
c′ a′
O X
b′
a′
X
O
a b
a
1 2 3
c
4
b
5
已知
作图
4.两直线相交
V c
a
k C A K
b
d D d B
O X H
交点是两直 线的共有点
c a a c
k
b d
O
X
a c
k
b
d k b
（1）投影特性 若两直线在空间相交，则各同面投影除了积聚 和重影外必相交，且交点符合点的投影规律。
V
a′
c′
b′
C
A c
B
若点在直线上,则点 的投影必在直线的同面 投影上，并符合点的投 影规律。 b′ Z ″
a
X
′
b″ c ″W
a″
c′
b
c″
O
a″

线,面的投影

线,面的投影
（2）平面在另两个投影面上的投影为原平面图 形的类似形，且小于实形。
正向、逆向 两个角度！
抓住只与一个
(2)投影面平行面 面平行！
水平面
a′
正平面
x
侧平面
a
b′ z c′
b″
a″ c″
yW
bc yH
图2-34 投影面平行面
投影面平行面的投影特性
水平面Ｑ q′
Ｑ
q″
q
水平面Ｑ的三面投影
q′
q″
q
各种位置直线的投影小结
⒈ 一般位置直线
三个投影与各投影轴都倾斜。
⒉ 投影面平行线
在其平行的投影面上的投影反映线段实长 及与相应投影面的夹角。另两个投影平行于相 应的投影轴。
⒊ 投影面垂直线
在其垂直的投影面上的投影积聚为一点。 另两个投影反映实长且垂直于相应的投影轴。
平面的投影
和直线投影又 类似又区别！
显实性（真实性或实形性）
3）类似性
当空间直线或平面倾斜于投影面时，其投影 仍为直线或与之类似的平面图形，其投影的长度变 短或面积变小，这种投影性质称为类似性。
类似性
说明同一个物体在 不同的投影面上的
表现不同！
三面投影及其对应关系
1.思考： 如图所示，三个不同形状的物体在一个投影面
上的投影完全相同。这说明形体的一个视图是不能 确定该形体在空间的形状和结构。
A1
B1
F1 H1
A1
B1
E1 D1
C1
假设光线能穿透物体
E1 D1 S C1
投影中心
投
影
物体
的
概 念 投影面
投影线 投影
投影法：用投影表示物体形状和大小的方法成为投影法。

面的投影

面的投影
x
c a
a’
e’
d’
d’
b’
0
a
b c
d
0
c’
a’
x
b’
(5)任意几何形：
c
a
b
e
a
c’ c
0
d
b
二．平面的投影特性
1.投影面垂直面
(1)定 ： 义 ——总有一个投影积聚为直线
H 铅 V 面的平面称为正垂面 W 侧 垂直于
(2)投影规律:
在所垂直的投影面上的投影积聚为直 线,且反映与另二投影面的倾角大小； 在另二投影面上的投影均为类似形。
正垂面
铅垂面
2.投影面平行面 —— 总有两个投影积聚为直线
(1)定 义：
平行于 H 水 V 面的平面称为正平面 W 侧
(2)投影规律:
在所平行的投影面上的投影反映实形； 在另二投影面上的投影均积聚为直线。
水平面
正平面
3.一般位置平面
(1)定 义： 与三投影面均倾斜的平 面称为一般位置平面。
(2)投影规律: 三面投影均不反映实 形，而为类似型。 一般位置平面
练习1:已知立体上平面P、Q、R的空间位置， 在投影图中标注其投影位置,并填空。
r’
q’
r ’’
p’’
q ’’
p’
r
p
q
水平 铅垂 侧垂
练习2:已知平面的两个投影,求作其第三投影,并填空。
（1） 1’
4’
6’
2’
’’ 1
’’ 2
（2）
1’
3’
’’ 6
2’ 4’
3’
5’
)’’5’’4’’2(’’1
例：如图所示，已知平面四边形的水平投影abcd 和AB、BC两边的正面投影，要求完成此四边行的 正面投影。

第三章：点、线、面的投影

三个投影都缩短了。 三个投影都缩短了。即: 都不反映空间线段的实长及与 三个投影面夹角， 三个投影面夹角，且与三根投 影轴都倾斜。 影轴都倾斜。
b
H
Y
一般位置直线求实长
• 直角三角形法求实长
投影面平行线
V b' a' A
β γ
a" W b" O
B X
β
a
γ
b
H
Y
(2) 投影面平行线 水平线
α
●
b a
●
●
b
●
a≡b≡m
直线倾斜于投影 直线平行于投影面 投影比空间线段 投影反映线段实长 ab=AB cosα ab=AB 真实性
直线垂直于投影 投影重合为一点 ab=0 积聚性
⒉ 直线在三个投影面中的投影特性
正平线（平行于Ｖ 正平线（平行于Ｖ面） 侧平线（平行于Ｗ 投影面平行线 侧平线（平行于Ｗ面） 平行于某一投影面而 水平线（平行于Ｈ 水平线（平行于Ｈ面） 统称特殊位置直线 与其余两投影面倾斜
X
a′ ′
●
az
Z
●
a″ ay
Y
ax a
●
O
Y
ay
② aax= a″az=y=A到V面的距离 ″ 到 面的距离 a′ax= a″ay=z=A到H面的距离 ′ ″ 到 面的距离 aay= a′az=x=A到W面的距离 ′ 到 面的距离
二、各种位置直线的投影特性
⒈ 一般位置直线
三个投影与各投影轴都倾斜。 三个投影与各投影轴都倾斜。
⒉ 投影面平行线
在其平行的投影面上的投影反映线段实长 及与相应投影面的夹角。另两个投影平行于相 及与相应投影面的夹角。 应的投影轴。 应的投影轴。

面的投影


b a c
V
b a B A C c H a b a
正平面 b b a c
c
W
a
c
c
b c
b
a
侧平面
V b b a c
b c a
B
A
b
W a
a c a b c
a
b
C Hc
c
积聚性 ABC为什么位 置的平面 a b c a c
积聚性 b
水平面
以铅垂面为例其投影特点：
１) 铅垂面的水平投影为一直线（正投影的积聚性） 并反映β、γ实际大小 ２) 铅垂面的正面投影和侧面投影成类似图形 正垂面、侧垂面也有类似特点 V P A a c H B PHb C W a a
c
b
a
c
b

c

b
正垂面
V
a c QV A
b
c α a BW
m a
b
n c b m n c

a
例 2-3 ３：已知四边形 ABCD 的两 面投影，在其上取一 K点，使点K 在 H面之上10mm，在V面之前15mm。
作图分析： 可在四边形 ABCD 内作位于 H 面之 上 10mm 的水平线 EF ，再在 EF 上取位 于V面之前15mm的点K。
四．过点或直线作平面 1.过点作平面 过一点可作无数个一般位置平面。
二、各种位置平面的投影特性 平面在三投影面体系中的投影特性 正垂面
垂直于某一投影面，倾 斜于另两个投影面
投影面垂直面
特殊位置平面
侧垂面 铅垂面 正平面
平行于某一投影面， 垂直于另两个投影面
投影面平行面
侧平面 水平面
与三个投影面都倾斜

面的投影教案

面的投影教案教案标题：面的投影教案教案目标：1. 学生能够理解面的投影是指一个物体在一个平面上的影子。

2. 学生能够通过观察和实践，掌握面的投影的基本概念和方法。

3. 学生能够应用面的投影的知识解决与日常生活相关的问题。

教学重点：1. 面的投影的定义和基本概念。

2. 面的投影的方法和步骤。

3. 面的投影在实际生活中的应用。

教学难点：1. 学生理解面的投影的概念和方法。

2. 学生能够将面的投影应用到实际生活问题中。

教学准备：1. 投影仪或幻灯机。

2. 平面图纸和铅笔。

3. 一些立体物体，如正方体、长方体等。

教学过程：引入（5分钟）：1. 引导学生回忆并讨论他们对投影的理解和经验。

2. 提出问题：“你们曾经见过物体的投影吗？你们知道什么是面的投影吗？”探究（15分钟）：1. 使用投影仪或幻灯机，展示一些物体在平面上的投影图像。

2. 解释面的投影的概念和定义：“面的投影是指一个物体在一个平面上的影子。

”3. 给学生分发平面图纸和铅笔，让他们在纸上绘制一个简单的平面图形。

4. 让学生使用立体物体在纸上投影，观察投影图像。

讲解（10分钟）：1. 解释面的投影的方法和步骤：a. 选择一个合适的平面作为投影面。

b. 将物体放置在投影面上，并保持物体与投影面垂直。

c. 使用光线或投影仪，观察物体在投影面上的影子。

d. 根据观察到的影子，绘制物体的投影图像。

实践（15分钟）：1. 让学生分组，每组选择一个立体物体。

2. 让每组学生使用平面图纸和铅笔，按照讲解的方法和步骤，绘制物体的投影图像。

3. 学生互相交换投影图像，并进行对比和讨论。

拓展（10分钟）：1. 引导学生思考面的投影在实际生活中的应用。

2. 提出问题：“你们能想到哪些日常生活中使用面的投影的例子？”3. 让学生分享他们的观点和例子，并进行讨论。

总结（5分钟）：1. 复习面的投影的概念和方法。

2. 强调面的投影的重要性和应用。

3. 鼓励学生在日常生活中运用面的投影的知识解决问题。

面的投影


投影面垂直面在三面投影体系中的投影如表所示。
投影面垂直面的投影特性： “两框一斜线”
1) 在所垂直的投影面上的投影为有积聚性的直线段； 2) 其他的投影为原形的类似形。
铅垂面
水平投影积聚为直线， 并反映倾角β、γ的实形； 正面投影和侧面投影均 不反映实形且变小。 Z
V
Z
β
γ
W O X O
YW
X
β
γ
投影面平行面在三面投影体系中的投影如表所示。
投影面平行面的投影特性： “一框两直线”
①在所平行的投影面上的投影反映实形； ②其他投影为有积聚性的直线段，且平行于相应的投 影轴。
水平面
Z V p' p" P W X
水平投影反映实形； 正面投影和侧面投影 积聚为一条直线并平 行于相应的投影轴。 Z
p' O
表
名称
立 体 图
投影面平行线
正平线 侧平线
水平线
投 影 图
名称
在形 体投 影图 中的 位置 在形 体立 体图 中的 位置
水平线
正平线
侧平线
4.3.2.2.3 投影面垂直线
垂直于一个投影面而平行于另两个投影面的直 线称为投影面垂直线。投影面垂直线也可分为：
（1）铅垂线——⊥H面，∥V面和W面； （2）正垂线——⊥V面，∥H面和W面； （3）侧垂线——⊥W面，∥H面和V面。
YH
表 投影面垂直面
名称
立 体 图
铅垂面
正垂面
侧垂面
投 影 图
投影特性“两框一斜线”
4.3.3.2.3 一般位置平面
与三个投影面既不平行也不垂直（倾斜）的平
面称为一般位置的平面。 一般位置的平面在三个投影面上的投影都不反 映实形，也不积聚成直线，均是平面的类似形。如 图所示。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第4章 平面的投影
4.1 平面的表示法 4.2 平面对投影面的各种相对位置 4.3 平面上的点和直线
4.1 平面表示法
一、几何元素表示法



(a)三点表示平面
(b)一点一直线
(c)两相交直线


(d)两平行直线
(e)平面图形
二、迹线表示法 ：
迹线：平面与投影面的交线称为迹线
平面P与H面的交线称为水平迹线，用PH表示； 平面P与V面的交线称为正面迹线，用PV表示； 平面P与W面的交线称为侧面迹线, 用PW表示。
例4：在平面ABC内作正平线和水平线
例5：在平面ABC内作一点K，使其与H面相距 40mm，与V面相距20mm。
α

平面在与其所垂直的投影面上的投影积聚成 倾斜于投影轴的直线,并反映该平面对其他两个 投影面的倾角 平面的其他两个投影都是面积小于原平面图 形的类似形
例1：求平面的水平投影，并判断其空间位置 1、分析：平面为正 垂面，其水平投影为 原图形的类似形。 2、作图：根据平面 的正面和侧面投影， 分别作出平面上各顶 点的水平投影 3、连点：顺序连接 各点的水平投影， 并描深图线 4、结果
3、侧平面的投影特性
W面投影△abc反映实形 H面投影和V面投影积聚成直线 且 abc//OY, abc //OZ
平面在与其平行的投影面上的投影反映平 面图形的实形 平面在其他两个投影面上的投影均积聚成 平行于相应投影轴的直线
三、一般位置平面
三个投影都为原平面图形的类似形 面积均比实形小 不反映 、、 的真实角度
4.2 平面对投影面的各种相对位置
平面倾角 ：是指平面与某一投影面所成的二面角，
分别用、、表示平面对投影面H、V、W的倾角 。
一、投影面垂直面
1、正垂面的投影特性
正面投影积聚成一条直线abc H和Ｗ投影都是类似的三角形△abc, △abc 反映倾角α、γ角的真实大小
例3：已知五边形ABCDE的一边BC//V面，完成 其水平投影
1、因为BC//V, 有 bc//ox，可确定c
2、作辅助线：连AC 3、连be, 求点e 4、连bd, 求点d 5、连接aedc，即为所求。
二、属于平面上的投影面平行线
既属于平面又与投影面平行的直线，称为属于 平面上的投影面平行线。有三类： 属于平面的水平线 属于平面的正平线 属于平面的侧平线 属于平面上的投影面平行线几何条件： 既要符合投影面平行线的投影特性 又要符合直线在平面上的投影特点
4.3 平面上的点和直线
一、属于平面上的点和直线的几何条件
1、在平面上作点
点在平面上的几何条件是：点在平面内的一条 直线上 已知：AB在平面P上 点C在直线AB上 则： 点C在平面P上
B C A P
2、在平面上作直线
例1: 已知点K在ABC上，试求点K的正面投影。
例2: 判断点M是否在平面ABC内
2、铅垂面的投影特性
水平投影积聚成一条直线 abc V和Ｗ投影都是类似的三角形△abc, △abc 反映倾角、γ角的真实大小
3、侧垂面的投影特性
侧面投影积聚成一条直线abc V和H投影都是类似的三角形△abc, △abc 反映倾角α 、角的真实大小
二、投影面平行面
1、正平面的投影特性
平行V面而同时垂直其它两个投影面的平面叫正平面
c
C B
X
z
b
c
b
a
o
b
a
YW
A a c V面投影△abc反映实形 H面投影和W面投影积聚成直线 且 abc//OX, abc //OZ
yH
Байду номын сангаас
2、水平面的投影特性
H面投影△abc反映实形 V面投影和W面投影积聚成直线 且 abc //OX, abc //OY