王建邦经典试题知识点

第13讲平面向量十大题型总结【题型目录】题型一：平面向量线性运算题型二：平面向量共线问题题型三：平面向量垂直问题题型四：平面向量的夹角问题题型五：平面向量数量积的计算题型六：平面向量的模问题题型七：平面向量的投影问题题型八：万能建系法解决向量问题题型九：平面向量中的最值范围问题题型十：平面向量中多选题【典型例题】题型一：平面向量线性运算【例1】在ABC △中，D 是AB 边上的中点，则CB =（）A ．2CD CA+ B ．2CD CA- C ．2CD CA- D ．2CD CA+ 【答案】C【解析】：CA CD AC CD CD AC CD AD CD DB CD CB -=+=++=+=+=22【例2】在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB =A ．3144AB AC-B ．1344AB AC-C ．3144+AB AC D ．1344+AB AC 【答案】A【解析】根据向量的运算法则，可得()111111222424BE BA BD BA BC BA BA AC=+=+=++ 1113124444BA BA AC BA AC=++=+，所以3144EB AB AC =-，故选A.【例3】在ABC 中，点P 为AC 中点，点D 在BC 上，且3BD DC = ，则DP =()A ．1144AB AC+B ．1144AB AC--C ．1144AB AC-D ．1144AB AC-+【答案】B【解析】∵点P 为AC 中点，∴12AP AC = ,∵3BD DC =，()3AD AB AC AD ∴-=- ,∴1344AD AB AC =+ ,∴113244DP AP AD AC AB AC =-=-- =1144AB AC --,故选：B.【例4】在ABC 中，AD 为BC 边上的中线，E 为AD 的中点，且EB AB AC λμ=+，则λ=________，μ=_________．【答案】3414-【解析】如下图所示：D Q 为BC 的中点，则()()111222AD AB BD AB BC AB AC AB AB AC =+=+=+-=+，E 为AD 的中点，所以，()1124AE AD AB AC ==+，因此，()131444EB AB AE AB AB AC AB AC =-=-+=- ，即34λ=，14μ=-.故答案为：34；14-.【例5】如图，等腰梯形ABCD 中，3AB BC CD AD ===，点E 为线段CD 中点，点F 为线段BC 的中点，则FE =（）A ．2136AB AC+B ．2136AB AC-+C ．1263AB AC+D ．1263AB AC-+点F 为线段BC 的中点，13BD BA AD BA BC BA =+=+=+ 又2BD FE = ，2136FE AB AC ∴=-+.【题型专练】1.设,,D E F 分别为ABC 的三边BC,CA,AB 的中点，则EB FC +=()A ．ADB ．12ADC ．12BCD ．BC【答案】A【解析】111()()()222EB FC BA BC CA CB AB AC AD +=-+-+=+=，故选：A2.设D为△ABC所在平面内的一点,若3,AD BD CD CA CBλμ==+,则μλ=_____.【答案】3-【解析】如图所示：3CD CA AD CA BD=+=+，CA=+3(CD CB-)，即有CD=﹣1322CA CB+，因为CD CA CBλμ=+，所以λ=﹣12，μ=32，则μλ=﹣3，故答案为：﹣3.3.在ABC中，4AC AD=，P为BD上一点，若13AP AB ACλ=+，则实数λ的值（）A．18B．316C．16D．38【答案】C【解析】4AC AD=，14AD AC∴=，则14BD AD AB AC AB=-=-，1233BP AP AB AB AC AB AC ABλλ⎛⎫=-=+-=-⎪⎝⎭，由于P为BD上一点，则//BP BD，设BP k BD=，则21344kAC AB k AC AB AC k ABλ⎛⎫-=-=-⎪⎝⎭，所以423kkλ⎧=⎪⎪⎨⎪=⎪⎩，解得16λ=.4.在ABC 中，2AB =，4BC =，60ABC ∠=︒，AD 为BC 边上的高，O 为AD 的中点，若AO AB BC λμ=+，则λμ+=（）A ．13B ．23C ．38D ．58【答案】D【解析】AD 是BC 边上的高，∴90ADB ∠=︒，在ADB △中，1cos 22BD BD ABD AB ∠===，解得1BD =， 4BC =，∴14BD BC =，∴14AD AB BD AB BC =+=+， O 为AD 中点，∴1111122428AO AD AB BC AB BC ⎛⎫==+=+ ⎪⎝⎭ ， AO AB BC λμ=+ ，∴1128AB BC AB BC λμ+=+ ，∴12λ=，18μ=，∴115288λμ+=+=.5.已知O 是ABC 所在平面内一点，D 为BC 边中点，且20OA OB OC ++=，那么（）A ．AO OD =B ．2AO OD=C ．3AO OD=D ．4AO OD =【答案】A【解析】D 为BC 边中点，∴2OB OC OD +=，∵20OA OB OC ++=，∴0OA OD =+，即AO OD =.6．设D 为ABC 所在平面内一点，且满足3CD BD =，则（）A ．3122AD AB AC =-B ．3122=+AD AB ACC ．4133AD AB AC =-D ．4133AD AB AC=+ ∴2CB BD =，即12BD CB = .()12123122AD AB BD ABCBAB AB ACAB AC ∴=+=+=+-=- 故选：A.题型二：平面向量共线问题【例1】已知向量()1,2a =- ，()sin ,cos b αα= ，若//a b，则tan α=（）A ．12-B ．2-C ．12D ．2【例2】与模长为13的向量()12,5d =平行的单位向量为（）A ．1251313⎛⎫ ⎪⎝⎭，B ．1251313⎛⎫-- ⎪⎝⎭，C ．1251313⎛⎫ ⎪，或1251313⎛⎫-- ⎪，D ．1251313⎛⎫- ⎪，或1251313⎛⎫- ⎪，【例3】已知向量()1,2AB =，(),7BC m =，()3,1CD =-，若A ，B ，D 三点共线，则m =________．【例4】设向量,a b 不平行，向量λ+a b 与2+a b 平行，则实数λ=___．【答案】21【解析】因向量λ+a b 与2+a b 平行，所以()b a b a ba μμμλ22+=+=+，所以⎩⎨⎧==μμλ21，解得⎪⎩⎪⎨⎧==2121μλ【例5】在ABC ∆中，点P 满足3BP PC = ，过点P 的直线与AB 、AC 所在的直线分别交于点M 、N ，若AM AB λ= ，()0,0AN AC μλμ=>>，则λμ+的最小值为（）A ．212+B ．12+C ．32D ．52【答案】B【解析】如下图所示：3BP PC = ，即()3AP AB AC AP -=- ，1344AP AB AC∴=+ ，AM AB λ= ，()0,0AN AC μλμ=>> ，1AB AM λ∴=，1AC ANμ= ，1344AP AM ANλμ∴=+ ，M 、P 、N 三点共线，则13144λμ+=.()133********λμλμλμλμμλ⎛⎫∴+=++=++≥=+ ⎪⎝⎭，当且仅当μ=时，等号成立，因此，λμ+的最小值为312+，故选：B.【题型专练】1.已知非零向量a ，b ，c ，若(1)a x = ，，(41)b =- ，，且//a c ，//b c则x =（）A ．4B ．4-C ．14D ．14-【答案】D【解析】：因非零向量c b a ,,，且//a c ，//b c ，所以a 与b 共线，所以()x 411=-⨯，所以41-=x 2.已知向量的(7,6)AB =，(3,)BC m =- ，(1,2)AD m =- ，若A ，C ，D 三点共线，则m =______.3.已知向量a ，b 是两个不共线的向量，且35OA a b =+，47OB a b =+，OC a mb =+，若A ，B ，C 三点共线，则m =（）A ．1B ．1-C ．2D ．2-【答案】A【解析】法一：b a b a b a OB AO AB 27453+=++--=+=，()b m a b m a b a OC BO BC 7374-+-=++--=+=，因A ，B ，C 三点共线，所以AB 与BC 共线，所以()[]()b m a b m a b a 73732-+-=-+-=+λλλ，所以()⎩⎨⎧-=-=7231m λλ，解得⎪⎩⎪⎨⎧=-=131m λ法二：由,,A B C 三点共线，得(1)(4)(72)OC xOA x OB x a x b =+-=-+-，故41,72,x x m -=⎧⎨-=⎩解得1m =．4.设12e e，是两个不共线的向量，若向量12m e ke =-+（k ∈R ）与向量212n e e =-共线，则A ．0k =B ．1k =C ．2k =D ．12k =【答案】D【解析】因为向量12=-+ m e ke （k ∈R ）与向量212=-n e e 共线，所以存在实数λ，使得λ=m n ，所以有2211(2)λ-+=- e ke e e ，因此12k λλ=⎧⎨-=-⎩，解得12k =.5.如图，在ABC 中，点O 是BC 的中点，过点O 的直线分别交直线AB ，AC 于不同的两点M N ，，若AB mAM = ，AC nAN =，则m n +=（）A ．1B ．32C ．2D ．3【答案】C【解析】连接AO ，由O 为BC 中点可得，1()222m n AO AB AC AM AN =+=+，M 、O 、N 三点共线，122m n∴+=，2m n ∴+=.故选：C.6.已知M 为ABC 的边AB 的中点，N 为ABC 内一点，且13AN AM BC =+ ，则AMNBCNS S =△△（）A ．16B ．13C ．12D ．23【答案】B【解析】因为13AN AM BC =+，所以13MN BC = ，所以MN ∥BC ，又因为M 为边AB 的中点，所以点A 到MN 的距离等于点N 到BC 的距离，所以13AMNBCNMN S S BC== △△,题型三：平面向量垂直问题【例1】已知向量(1)(32)m =-，，=，a b ，且()+⊥a b b ，则m =（）A ．8-B ．6-C ．6D ．8【答案】D【解析】：()()()2,42,3,1-=-+=+m m b a ，因()b b a ⊥+，所以()0=⋅+b b a ，即()()()022122,32,4=--=--m m ，所以8=m 【例2】已知单位向量a ，b 的夹角为45°，ka –b 与a 垂直，则k =__________.【答案】22【解析】由题意可得：11cos 452a b →→⋅=⨯⨯=，由向量垂直的充分必要条件可得：0k a b a →→→⎛⎫-⋅= ⎪⎝⎭，即：202k a a b k →→→⨯-⋅=-=，解得：22k =.【例3】已知单位向量,a b 的夹角为60°，则在下列向量中，与b 垂直的是（）A ．b a 2+B ．ba +2C ．ba 2-D ．ba -2【答案】D【思路导引】根据平面向量数量积的定义、运算性质，结合两平面向量垂直数量积为零这一性质逐一判断即可．【解析】由已知可得：11cos 601122⋅=︒=⨯⨯=a b a b ．A ：∵215(2)221022+⋅=⋅+=+⨯=≠a b b a b b ，∴本选项不符合题意；B ：∵21(2)221202+⋅=⋅+=⨯+=≠a b b a b b ，∴本选项不符合题意；C ：∵213(2)221022-⋅=⋅-=-⨯=-≠a b b a b b ，∴本选项不符合题意；D ：∵21(2)22102-⋅=⋅-=⨯-=b b b a b b ，∴本选项符合题意．故选D ．【例4】已知向量(2,1),(3,)a b m →→=-=，且()a b a →→→+⊥，则实数m =___________.【答案】1【分析】先求出+=(1,1)a b m →→+，再解方程1(2)1(1)0m ⨯-+⨯+=即得解.【详解】解：由题得+=(1,1)a b m →→+，因为()a b a →→→+⊥，所以()=0a b a →→→+g ，所以1(2)1(1)0,1m m ⨯-+⨯+=∴=.故答案为：1【例5】已知非零向量m,n 满足4|3|=m |n |，1cos ,3<>=m n ．若()t ⊥+n m n ，则实数t 的值为（）A ．4B ．–4C ．94D ．–94【答案】B 【解析】由()t ⊥+n m n 可得()0t ⋅+=n m n ，即20t ⋅+=m n n ，所以2221|cos |3||t |||<,>|||=-=-=-⋅⋅⨯⨯n n n m n m n m n m n ||4334||3=-=-⨯=-n m ．故选B ．【例6】已知向量AB 与AC 的夹角120，且|AB |=3，|AC |=2，若AP AB AC λ=+ ，且AP BC ⊥ ，则实数λ的值为_____．【答案】712【解析】向量与的夹角为，且所以．由得，，即，所以，即，解得．【题型专练】1.ΑΒC ∆是边长为2的等边三角形，已知向量a ，b 满足2ΑΒ= a ，2ΑC =+a b ，则下列结论正确的是（）A ．1=b B ．⊥a bC ．1⋅=a b D ．()4ΒC-⊥a b 【答案】D【解析】如图由题意，(2)2BC AC AB a b a b =-=+-= ，故||2b = ，故A 错误；|2|2||2a a ==，所以||1a = ，又22(2)4||222cos 602AB AC a a b a ab ⋅=⋅+=+=⨯=，所以1a b ⋅=- ，故,B C 错误；设,B C 中点为D ，则2AB AC AD += ，且AD BC ⊥ ，所以()4C a b +⊥B ，故选D ．2.已知1e ，2e 12-e 与12λ+e e 的夹角为60 ，则实数λ的值是．【答案】33【解析】解法一：因1e ，2e 11==，021=⋅e e所以221212112122)()λλλ-⋅+=+⋅-⋅-=-e e e e e e e e ，12|2-=e ，12||λ+===e e ，2cos60λ==，解得：33λ=．解法二：建立坐标系，设()()1,0,0,121==e e ()()λλ,1,1,3212=+-=-e e e ，所以()()2221213λ+=+=-+=)()λλ-=+-3212e e e所以由数量积的定义得︒⨯+⨯=-60cos 1232λλ，解得：33λ=．3.已知向量()(),2,1,1a m b ==，若()a b b +⊥ ，则m =__________.【答案】4-【分析】根据向量的坐标运算即可求解.【详解】由题意可得()1,3a b m +=+，则130m ++=，解得4m =-.故答案为：4-4.已知向量(,2),(2,4)m a a n a =+=- ，且()n m n ⊥-，则实数=a _____________．【答案】2【分析】根据向量坐标运算及向量垂直的坐标表示即得.【详解】因为(,2)(2,4)(2,2)m n a a a a -=+--=-，又()n m n ⊥- ，所以2(2)(2)40a a ⨯-+-⨯=，解得2a =．故答案为：2.5.在ABC 中，()1,2,3A k -，()2,1,0B -，()2,3,1C -，若ABC 为直角三角形，则k 的值为（）A ．23B ．83C ．－1D ．325-题型四：平面向量的夹角问题【例1】已知平面向量a ，b满足||4,||1== a b ，()a b b -⊥ ，则cos ,a b 〈〉= （）A ．14B ．4C．4D ．4【例2】已知(2,0)a = ，1,22b ⎛= ⎝⎭r ，则a b - 与12a b + 的夹角等于（）A ．150°B ．90°C ．60°D ．30°【例3】已知向量a=（2，1），()3,1b =- ，则（）A．若c =-⎝⎭ ，则a c ⊥B ．向量a 在向量b 上的投影向量为12b-C ．a 与a b -D ．()//a b a+【例4】若向量a ，b 满足||a = ，(2,1)b =-，5a b ⋅=- ，则a 与b 的夹角为_________．【例5】已知向量a b ，满足566a b a b ==⋅=-，，，则cos ,a a b +=()A ．3135-B ．1935-C ．1735D ．1935【例6】若非零向量,a b 满足32a b a b ==+，则a 与b 夹角的余弦值为________．【例7】设向量(68)=-，a ，(34)=，b ，t =+c a b，t ∈R ，若c 平分a与b 的夹角，则t 的值为．【答案】2【解析】解法一：()t t b t a c 48,36++-=+=，所以()()t t t c a 14100488366+=+++--=⋅；()()1425484363+=+++-=⋅t t t c b 510==因c 平分a 与b 的夹角，所以=c b c a ==，所以()1425214100+=+t t ，解得2=t解法二：因c 平分a 与b的夹角，所以()()⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛+-=⎫⎛=58,054,3108,6λλλb a c ，又因()t t b t a c 48,36++-=+=，所以()()t t 3658480+-=+⨯，解得2=t 【例8】已知A B C △的三个顶点分别为(3(60)(5A B C ，，，，，求ACB ∠的大小．【答案】C【解析】()()3,1,0,2=-=CB CA()()()2312022222=+==+-=所以21223012cos -=⨯⨯+⨯-==∠CB CA ACB ，所以︒=∠120ACB 【题型专练】1.设非零向量、ab满足||2||,||||a b a b b =+= ，则向量a 与b的夹角为（）A ．30°B ．60︒C ．120︒D ．150︒2.已知(2,1)a =-，||b =，且()10a b a +⋅= ，则,a b 〈〉= ___________.3.已知向量,a b 满足||1a =，||a b =+1)b =- ，则,a b 的夹角等于___________.4.若两个非零向量a 、b 满足2a b a b a +=-=，则a b - 与b 的夹角___________.5.已知单位向量a ，b 满足0a b ⋅=，若向量c =+，则sin ,a c ＝（）A B C D6.已知向量,a b 满足()()3,4,·28a b a b a b ==+-=，则向量a 与b 所成的夹角为（）A ．π6B ．π3C ．π2D ．2π37.已知向量a ，b 满足||2||2b a == ，|2|2a b -= ，则向量a ，b 的夹角为（）A ．30°B ．45︒C ．60︒D ．90︒8.已知向量()PA =，(1,PB =，则APB ∠=A ．30︒B ．60︒C ．120︒D ．150︒【答案】D【解析】根据题意，可以求得2,2PA PB ===，所以333cos 222PA PB APB PA PB⋅∠===-⋅，结合向量所成角的范围，可以求得150APB ∠=︒，故选D ．9.非零向量a ，b 满足：-=a b a ，()0⋅-=a a b ，则-a b 与b 夹角的大小为A ．135︒B ．120︒C ．60︒D ．45︒【答案】A【解析】 非零向量a ，b 满足()0⋅-=a a b ，∴2=⋅a a b，由-=a b a 可得2222-⋅+=a a b b a，解得=b ，()22cos 2θ-⋅⋅-∴===--a b ba b b a b ba b，θ为-a b 与b 的夹角，135θ∴= ，故选A ．10.已知a ，b 为单位向量，且a ·b =0，若2=c a ，则cos,=a c ___________.【答案】23【解析】因为2=c a，0⋅=a b ，所以22⋅=⋅a c a b 2=，222||4||5||9=-⋅+=c a b b ，所以||3=c ，所以cos ,=a c 22133⋅==⨯⋅a c a c ．11.已知向量(4,3),(1,2)a b =-=-，,a b的夹角为θ，则sin θ=__________.【答案】55【解析】依题意[]0,πθ∈，所以255cos ,sin 55||||a b a b θθ⋅===-== .故答案为.12.已知向量,a b 满足5,6,6==⋅=-a b a b ，则cos ,+=a a b （）A ．3531-B ．3519-C ．3517D ．3519【答案】D【思路导引】计算出()a ab ⋅+ 、a b + 的值，利用平面向量数量积可计算出cos ,a a b <+>的值．【解析】5a = ，6b = ，6a b ⋅=- ，()225619a a b a a b ∴⋅+=+⋅=-= ．7a b +== ，因此()1919cos ,5735a ab a a b a a b ⋅+<+>===⨯⋅+ ．故选D ．题型五：平面向量数量积的计算【例1】（2021新高考2卷）已知向量0,||1,||||2,a b c a b c a b b c c a ++====⋅+⋅+⋅=_______．【答案】29-【解析】方法一：因为0=++c b a ，所以()02=++cb a ，即0222222=+++++c b c a b a c b a所以0222441=+++++c b c a b a ，所以9222-=++c b c a b a ，所以29-=++c b c a b a 方法二：因为0=++c b a ，所以c b a -=+，所以()()22c b a -=+，即2222cb a b a=++所以4241=++b a ，所以21-=b a ，同理b c a -=+，所以()()22b ca -=+，即2222b c a c a =++，所以4241=++c a ，所以21-=c a ，同理a c b -=+，所以()()22a c b -=+，即2222a c b c b =++，所以1244=++c b ，所以27-=⋅c b ，所以29-=++c b c a b a 【例2】在△ABC 中，6,AB O =为△ABC 的外心，则AO AB ⋅等于A B ．6C ．12D ．18【答案】D【解析】试题分析：如图，过点O 作OD AB ⊥于D ，则()36018AO AB AD DO AB AD AB DO AB ⋅=+⋅=⋅+⋅=⨯+=，应选D.【例3】已知边长为3的正2ABC BD DC = ，，则AB AD ⋅=（）A ．3B ．9C ．152D ．6【例4】已知ABC 为等边三角形，AB =2，设点P ，Q 满足AP AB λ=，(1)AQ AC λ=-，R λ∈，若2BQ CP ⋅=-，则λ=（）A ．12B ．12C ．12±D故选：A.【例5】在ABC 中，6A π=，||AB =||4AC =，3BD BC =，则AB AD ⋅=______．【答案】24-【分析】利用基底,AB AC 3AD AB BD AB BC =+=+ ,BC AC = 23AD AB AC ∴=-+ ,∴()232AB A AB AD AB AB C =⋅-+=-⋅ 【题型专练】1.如图，在△ABC 中，AD ⊥AB ，BC =，1AD = ，则AC AD ⋅=（）A ．B CD ．3-2.在ABC 中，3AB AC ==，DC BD 2=﹒若4AD BC ⋅=，则AB AC ⋅=______．3.ABC 中，90C ∠=︒，2AC =，P 为线段BC 上任一点，则AP AC ⋅=（）A ．8B ．4C ．2D ．64.已知ABC 为等边三角形，D 为BC 的中点，3AB AD ⋅=，则BC =（）A BC ．2D ．45.如图，在ABC 中，3BAC ∠=，2AD DB =，P 为CD 上一点，且满足2AP mAC AB =+，若||3AC =，||4AB =，则AP CD ⋅的值为（）A ．-3B ．1312-C ．1312D ．1126．在平行四边形ABCD 中，AC ＝6，AB AD ⋅＝5，则BD ＝____________.【详解】AC AB BC AB AD =+=+ ，则2AC AB = 236226AD AB AD +=-⋅=，AD AB - ，则222BD AD AB AD =-⋅+ 7．已知在ABC 中，90C ∠=︒，4CA =，3CB =，D 为BC 的中点，2AE EB =，CE 交AD 于F ，则CE AD ⋅=_______【答案】73-##123-题型六：平面向量的模问题【例1】已知(1)t =，a ，(6)t =-，b ，则|2|+a b 的最小值为________．【答案】52【解析】：()()()40205362444462262,2222222+-=+-+++=-++=-+=+t t t t t t t t t t a对称轴2=t ，所以当2=t 时，524040202=+-=a 【例2】（2021新高考1卷）已知O 为坐标原点，点1(cos ,sin )P αα，2(cos ,sin )P ββ-，3(cos(),sin())P αβαβ++，(1,0)A ，则：A ．12||||OP OP = B ．12||||AP AP =C ．312OA OP OP OP ⋅=⋅D ．123OA OP OP OP ⋅=⋅ 【答案】AC 【解析】【详解】A ：1(cos ,sin )OP αα=，2(cos ,sin )OP ββ=- ，所以1||1OP == ，2||1OP == ，故12||||OP OP = ，正确；B ：1(cos 1,sin )AP αα=- ，2(cos 1,sin )AP ββ=-- ，所以1||2|sin |2AP α===== ，同理2||2|sin |2AP β== ，故12||,||AP AP 不一定相等，错误；C ：由题意得：31cos()0sin()cos()OA OP αβαβαβ⋅=⨯++⨯+=+，12cos cos sin (sin )cos()OP OP αβαβαβ⋅=⋅+⋅-=+ ，正确；D ：由题意得：11cos 0sin cos OA OP ααα⋅=⨯+⨯= ，23cos cos()(sin )sin()OP OP βαββαβ⋅=⨯++-⨯+()()()cos βαβcos α2β=++=+，故一般来说123OA OP OP OP ⋅≠⋅故错误；故选：AC【例3】已知向量a ，b 的夹角为60°，||2=a ，||1=b ，则|2|+a b =．【答案】324211244+⨯⨯⨯+====+3212==【例4】已知a 与b 均为单位向量，其中夹角为θ，有下列四个命题1p ：||1+>a b ⇔θ∈[0，23π）2p ：||1+>a b ⇔θ∈(23π，π]3p ：||1->a b ⇔θ∈[0，3π）4p ：||1->a b ⇔θ∈(3π，π]其中真命题是（A ）1p ，4p (B)1p ，3p (C)2p ，3p (D)3p ，4p 【答案】A【解析】由||1+>a b 得，221∙>a +2a b +b ，即∙a b ＞12-，即cos θ=||||∙a b a b ＞12-，∵θ∈[0，π]，∴θ∈[0，23π），由||1->a b 得，22-1∙>a 2a b +b ，即∙a b ＜12，即cos θ=||||∙a b a b ＜12，∵θ∈[0，π]，∴θ∈(3π，π]，故选A ．【例5】设a ，b 是两个非零向量A ．若||||||+=-a b a b ，则⊥a bB ．若⊥a b ，则||||||+=-a b a b C ．若||||||+=-a b a b ，则存在实数λ，使得λ=b a D ．若存在实数λ，使得λ=b a ，则||||||+=-a b a b 【答案】C【解析】对于A b b a a2222-=⇒+-=+⋅+⇒=θ，所以1cos -=θ，所以︒=180θ，所以A 错，B 错；C 对，D 有可能为︒0【题型专练】1．设向量(10)，a =，22()22=-b ，若t =+c a b (t ∈R)，则||c 的最小值为A B ．1C ．2D ．12【答案】C【解析】()⎪⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=+=t t t b t a c 22,22122,220,12222221⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛+=t t 222122122121212222≥+⎪⎪⎭⎫ ⎝⎛+=++=+++=t t t t t t 2.已知向量(1,2)a =- ，(21,1)b m =- ，且a b ⊥，则|2|a b -= （）A ．5B ．4C ．3D ．23.已知向量a ，b满足1a =，2b =，a b -=，则2a b +=（）A ．B ．C D4.已知[02π)αβ∈、，，(cos ,sin )a αα=r，(cos(),sin())b αβαβ=++，且23a b -=，则β可能为（）A ．π3B ．2π3C ．πD ．4π3【答案】BD【分析】根据向量模的运算列方程，化简求得cos β的值，进而求得正确答案.5.平面向量a 与b 的夹角为60︒，(3,4),||1==a b ，则|2|a b += _____________．6.已知向量,a b 满足||2,(2,2)a b == ，且|2|6a b += ，则||a b += __________．7.设,a b 为单位向量，且||1+=a b ，则||a b -=______________.【解析】因为,a b为单位向量，所以1a b ==r r所以1a b +==，解得：21a b ⋅=-所以a b -==8.设a ，b 均为单位向量，则“33-=+a b a b ”是“a ⊥b ”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】C【解析】∵33-=+a b a b ，∴22(3)(3)-=+a b a b ，∴2269-⋅+=a ab b 2296+⋅+a a b b ，又||||1==a b ，∴0⋅=a b ，∴⊥a b ；反之也成立，故选C ．9.已知向量a ，b 夹角为045，且|a |=1，|2-a b |b |=．【答案】．【解析】∵|2-a b |=平方得224410-= a a b +b ，即260--=|b |b |，解得|b |=（舍）题型七：平面向量的投影问题【例1】已知向量(2,1),(1,1)a b =-= ，则a 在b上的投影向量的模为（）A B ．12C ．2D ．1【例2】已知6a =，3b =，向量a 在b 方向上投影向量是4e ，则a b ⋅ 为（）A ．12B ．8C ．-8D ．2【例3】已知平面向量a ，b ，满足2a =，1b =，a 与b 的夹角为23π，2b 在a 方向上的投影向量为（）A ．1-B ．12aC ．12a - D ．1【例4】已知平面向量a ，b 满足2=a ，()1,1b =，a b +=r r a 在b 上的投影向量的坐标为（）A ．22⎛ ⎝⎭B ．()1,1C ．()1,1--D ．⎛ ⎝⎭【例5】已知O 为正三角形ABC 的中心，则向量OA 在向量AB 上的投影向量为（）A ．ABB C ．12AB-D ．12AB故选：C【例6】设向量a 在向量b 上的投影向量为m ，则下列等式一定成立的是（）A ．||a b m bb ⋅=⋅ B ．2||a b m bb ⋅=⋅ C ．m b a b⋅=⋅ D ．ma b a⋅=⋅【题型专练】1．已知()1,2a = ，()1,2b =- ，则a 在b上的投影向量为（）A ．36,55⎛⎫- ⎪B ．36,55⎛⎫- ⎪C ．36,55⎛⎫-- ⎪D ．36,55⎛⎫ ⎪2．如图，在平面四边形ABCD 中，120ABC BCD ∠=∠= ，AB CD =，则向量CD 在向量AB 上的投影向量为（）A ．2AB -B ．12AB -C ．12AB D ．2AB 【答案】B【分析】根据图形求出向量AB 与CD的夹角，再根据投影向量的公式进行求解即可.【详解】延长AB ，DC 交于点E ，如图所示，3.已知向量()1,3a =，()2,4b =-，则下列结论正确的是（）A ．()a b a+⊥r r r B ．2a b +=C ．向量a 与向量b 的夹角为34πD ．b 在a的投影向量是()1,34.已知()3,1a =-，()1,2b =，下列结论正确的是（）A ．与b同向共线的单位向量是⎝⎭B ．a 与bC ．向量a在向量b 上的投影向量为12,55⎛⎫ ⎪⎝⎭D ．15a b b⎛⎫-⊥ ⎪ 5.关于平面向量，有下列四个命题，其中说法正确的是（）A ．若1,,120a b a b ===︒，则()2a b a+⊥r r r B ．点()()1,1,3,2M N --，与向量MN同方向的单位向量为43,55⎛⎫- ⎪⎝⎭C ．若20a b a b a +=-=≠ ，则+r r a b 与a b - 的夹角为60°D ．若向量()()2,1,6,2a b =-= ，则向量b 在向量a 上的投影向量为2a-同方向的单位向量为6．己知空间向量||3,||2a b ==，且2a b ⋅=，则b 在a 上的投影向量为________．【答案】29a ##29a7.已知1a =，2b =，且()a ab ⊥+，则a 在b 上的投影向量为（）A ．b -B ．bC ．14b- D ．14b【答案】C 【详解】因为()a a b ⊥+ ，所以()0a a b ⋅+= ，即220,0a a b a a b +⋅=+⋅= ，又因为1a = ，设,a b 的夹角为θ，所以1a b ⋅=-，a 在b 上的投影为：cos b a b a θ⋅=⋅ ，所以a 在b 上的投影向量为214cos b a b b b ba b θ⋅⋅=⋅=⋅- .故选：C8.已知点(1,1)A -、(1,2)B 、(2,1)C --、(3,4)D ，则向量AB 在CD 方向上的投影为ABC．D．【答案】A【解析】AB =（2，1），CD =（5，5），则向量AB 在向量CD方向上的射影为22325515255)5,5()1,2(cos 22=⨯+⨯=+⋅==CD AB AB θ9.若向量,a b满足22a a b =+= ，则a 在b 方向上投影的最大值是AB．CD．【答案】B【详解】由题意2,22a a b =+= ，所以2||4164b a b +⋅+=，设,a b 的夹角为θ，则2||8cos 120b b θ++= ，所以212cos 8b bθ+=- ，所以a 在b 方向上投影为2123cos 2()(48b b a bb θ+=⨯-=-+，因为3b b +≥cos a θ≤ ，故选B.题型八：万能建系法解决向量问题边长为a 的等边三角形已知夹角的任意三角形正方形矩形平行四边形直角梯形等腰梯形圆建系必备（1）三角函数知识cos ,sin x r y r q q ==；（2）向量三点共线知识(1)OC OB OAl l =+-（对面女孩看过来）．【例1】如图，在等腰梯形ABCD 中，2,3,4AB BC CD BC BE ==== ，则CA DE ⋅=（）A ．43B ．154-C ．558-D ．6516-3315,0,,0,1,D C A ⎛⎛⎫⎛⎫【例2】如图，正八边形ABCDEFGH 中，若AE AC AF λμ=+()R λμ∈，，则λμ+的值为________．正八边形的中心【详解】、HD BF 所在的直线分别为x y 、轴建立平面直角坐标系，正八边形的中心M 点，3608⎛∠=∠=∠=∠= ⎝AOB COB AOH EOD 18045135-= ，所以22.5∠= BAC ，13522.5112.5∠-∠=-= HAB CAB ，所以∠HAC y 轴，、AOM MOC 为等腰直角三角形，2，则2=====OD OF OE OA OC ，()0,2F ，2===OM MC ，所以()2,2--A ，(2,-C【点睛】本题主要考查了平面向量坐标法解决几何问题，建立坐标系是解题的关键，还考查了向量的加法运算，考查方程思想及转化思想，属于中档题．【题型专练】1.如图，在梯形ABCD 中，//AB DC ，10AB =，7BC =，2CD =，5AD =，则AC BD ⋅=___________.则5,02A ⎛⎫- ⎪⎝⎭，532,2C ⎛⎫ ⎪ ⎪⎝⎭，15,02B ⎛⎫ ⎪⎝⎭，530,2D ⎛ ⎝953,22AC ⎛⎫∴= ⎪ ⎪⎝⎭ ，1553,22BD ⎛⎫=- ⎪ ⎪⎝⎭，AC BD ∴⋅ 故答案为：15-.2.已知正方形ABCD 的边长为2，点P 满足1()2AP AB AC =+ ，则||PD = _________；PB PD ⋅=_________．【答案】(1).(2).1-【解析】以点A 为坐标原点，AB 、AD 所在直线分别为x 、y 轴建立如下图所示的平面直角坐标系，则点()0,0A 、()2,0B 、()2,2C 、()0,2D ，()()()()1112,02,22,1222AP AB AC =+=+= ，则点()2,1P ，()2,1PD ∴=-，()0,1PB =- ，因此，PD == ()021(1)1PB PD ⋅=⨯-+⨯-=-.题型九：平面向量中的最值范围问题【例1】如下图，在平面四边形ABCD 中，AB BC ⊥，AD CD ⊥，3BCD π∠=，CB CD ==M 为边BC 上的动点，则AM DM ⋅的最小值为（）A ．83B ．214C ．114-D ．133-【例2】ABC 是边长为4的等边三角形，点D 、E 分别在边AC 、BC 上，且DE BC ⊥，则DA DE ⋅的最小值为（）AB ．C ．3D ．－3则(0,0),(2,23),(4,0)C A B【例3】四边形ABCD 中，4AB =，60A B ∠=∠=︒，150D ∠=︒，则DA DC ⋅的最小值为（）AB ．C ．3D ．－3∴90,60DCB E ∠=︒∠= ，设CE x =，则3,DC x DA =∴()423cos150DA DC x x ⋅=-⋅⋅ 所以当1x =时，DA DC ⋅的最小值为【例4】如图，在梯形ABCD 中，//AD BC ，2AD =，9BC =，5AB =，cos 5B =，若M ，N 是线段BC上的动点，且1MN = ，则DM DN ⋅的最小值为（）A ．134B ．132C ．634D ．352//AD BC ，32AD =，9BC =，5AB =(9,0)C ∴，∴3cos 5A xB AB ==，3,4A A x y ==9(3,4),(,4)2A D ∴，【例5】已知边长为2的菱形ABCD 中，点F 为BD 上一动点，点E 满足2BE EC =，3AE BD ⋅=-，则AF BE⋅的最小值为（）A ．0B ．23C ．43D ．2【例6】已知向量a，b，c共面，且均为单位向量，0a b⋅=，则ab c++的最大值是（）A B C1D1【例7】骑自行车是一种能有效改善心肺功能的耐力性有氧运动，深受大众喜爱，如图是某一自行车的平面结构示意图，已知图中的圆A （前轮），圆DABE △，BEC △，ECD 均是边长为4的等边三角形．设点P 为后轮上的一点，则在骑动该自行车的过程中，AC BP ⋅的最小值为（）A ．12B ．24C ．36D ．18故选：A【例8】已知AB AC ⊥ ，1AB t = ，AC t = ，若点P 是ABC ∆所在平面内一点，且4AB AC AP AB AC=+ ，则PB PC ⋅的最大值等于（）A ．13B ．15C ．19D ．21【答案】A【解析】以题意，以点A 为坐标原点，以AB 所在的直线为x 轴，AC 所在的直线为y 轴建立如图所示的平面直角坐标系，所以点(1,4)P ，1(,0)B t，(0,)C t ，所以11(1,4)(1,4)(1)(1)4(4)PB PC t t t t ⋅=----=-⨯--⨯- =1174t t --17-≤=13（当且仅当14t t =，即12t =时取等号），所以PB PC ⋅ 的最大值为13．故选A ．【题型专练】1．已知梯形ABCD 中，3B π∠=，2AB =，4BC =，1AD =，点P ，Q 在线段BC 上移动，且1PQ =，则DP DQ ⋅的最小值为（）A ．1B ．112C ．132D ．1142．在ABC 中，902A AB AC ∠=== ，，点M 为边AB 的中点，点P 在边BC 上运动，则AP MP ⋅的最小值为___________.【答案】78【分析】建立平面直角坐标系，利用数量积的坐标运算求出3.ABC 为等边三角形，且边长为2，则AB 与BC 的夹角大小为120，若1BD =，CE EA =，则AD BE ⋅的。

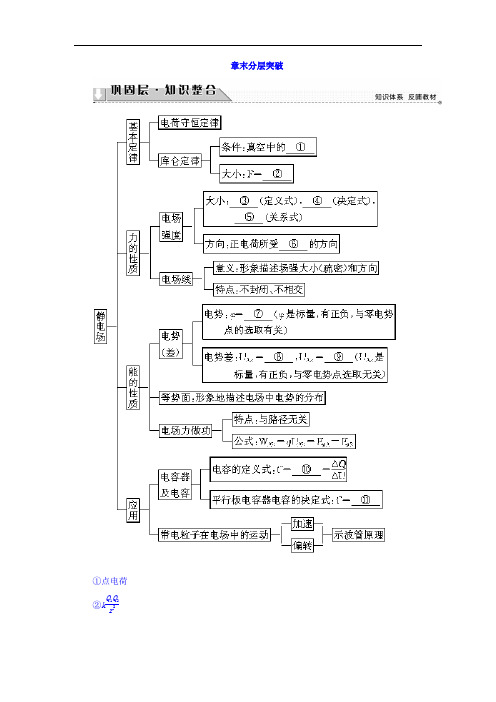
章末分层突破①点电荷②kQ 1Q 2r 2③E ＝F q④E ＝k Q r2 ⑤E ＝U d⑥电场力 ⑦E p q⑧W ABq⑨φA －φ B⑩Q U⑪εr S 4πkd线，a 、b 、c 三点所在直线平行于两电荷的连线，且a 与c 关于MN 对称，b 点位于MN 上，d点位于两电荷的连线上．以下判断正确的是()图1­1A ．b 点的电场强度大于d 点的电场强度B ．b 点的电场强度小于d 点的电场强度C．a 、b 两点间的电势差等于b 、c 两点间的电势差 D ．试探电荷＋q 在a 点时的电势能小于在c 点时的电势能【解析】 如题图所示，两电荷连线的中点位置用O 表示，在中垂线MN 上，O 点电场强度最大，在两电荷之间的连线上，O 点电场强度最小，即E b <E O ，E O <E d ，故E b <E d ，选项A 错误，选项B 正确；等量异种点电荷的电场中，等势线具有对称性，a 、c 两点关于MN 对称，U ab ＝U bc ，选项C 正确；试探电荷＋q 从a 移到c ，远离正电荷，靠近负电荷，电场力做正功，电势能减小，选项D 错误；另一种理解方法：a 点电势高于c 点电势，试探电荷＋q 在a 处的电势能大，在c 处的电势能小．【答案】 BC1．电场中某点的电势高低与该点的电场强度大小无关． 2．电场中沿电场线方向电势降低得最快．3．E 、φ、U 、E p 均有正、负之分，但只有E 是矢量．1.有区别：(1)电场线总与等势面垂直．电荷沿着电场线移动，电场力一定做功；电荷沿着等势面移动，电场力一定不做功．(2)在同一电场中，等差等势面的疏密也反映电场的强弱，等差等势面密集处，电场线也密集，电场强；反之，电场线稀疏，电场弱．(3)知道等势面，可画出电场线，知道电场线，也可画出等势面．2．带电粒子在电场中的运动轨迹是由电场力和初速度共同决定的，可以根据轨迹分析受到的电场力方向，进一步研究加速度、动能、电势能的变化等．如图1­2所示，在点电荷Q 产生的电场中，将两个带正电的试探电荷q 1、q 2分别置于A 、B 两点，虚线为等势线．取无穷远处为零电势点，若将q 1、q 2移动到无穷远的过程中外力克服电场力做的功相等，则下列说法正确的是( ) 【导学号：96322024】图1­2A ．A 点电势大于B 点电势 B ．A 、B 两点的电场强度相等C ．q 1的电荷量小于q 2的电荷量D ．q 1在A 点的电势能小于q 2在B 点的电势能【解析】 由于电场力做负功，所以Q 应带负电荷，由负点电荷产生电场的电场线的分布规律可判断出φB ＞φA ，故A 项错误；由E ＝k Qr2，r 不相等，知E A ≠E B ，故B 项错误；由φA ＝W A →∞q 1、φB ＝W B →∞q 2，因为W A →∞＝W B →∞，φA ＜φB ＜0，所以1q 1＞1q 2，即q 1＜q 2，故C 项正确；由于克服电场力做功相等，且无穷远处电势能为零，所以q 1在A 点的电势能等于q 2在B 点的电势能，故D 项错误．【答案】 C如图1­3所示，虚线表示等势面，相邻等势面间的电势差相等．有一带正电的小球在电场中运动，实线表示小球的运动轨迹．小球在a 点的动能为20 eV ，运动到b 点时动能为2 eV.若取c 点为零电势点，则当这个小球的电势能等于6 eV 时，它的动能为(不计重力和空气阻力)( )图1­3A．18 eV B．12 eVC．10 eV D．8 eV【解析】由于带电小球在电场中移动时，只有电场力做功，因此能量之间的转化只有动能和电势能之间的转化，因等势面为等差等势面，在相邻等势面间移送电荷，其动能变化相同，从a点到b点，动能减小了18 eV，所以从a点到c点动能减少了6 eV，c点动能为14 eV，故当小球电势能为6 eV时，它的动能为8 eV，D对．【答案】 D1.体的受力情况是解题的关键，通过受力分析可判断带电体的运动性质及运动轨迹．从力和运动的角度进行分析是解决带电体在电场中运动问题的最基本方法．2．分解的思想：带电体在电场和重力场的复合场中，若做类平抛或其他曲线运动，都可以考虑分解的思想，把它分解为两个分运动，可使问题很快得到解决3．功能关系：带电体在电场中运动的过程中伴随着做功和各种能量的转化，由于静电力做功与路径无关，这给动能定理和能量守恒定律提供了广阔的舞台．如图1­4所示，电荷量为－e、质量为m的电子从A点沿与电场垂直的方向进入匀强电场，初速度为v0，当它通过电场中B点时，速度与场强方向成150°角，不计电子的重力，设A点的电势为零，求B点的电势．图1­4【解析】电子进入匀强电场后在电场力作用下做匀变速曲线运动，根据运动的分解可知，电子在垂直于电场线方向上做匀速直线运动．将B点的速度分解(如图)v ＝v 0cos 60°＝2v 0电子从A 运动到B 由动能定理得：W ＝12mv 2－12mv 20＝32mv 20.电场力做正功，电势能减少，所以B 点的电势能为E p B ＝－32mv 20，φB ＝E p B q ＝－32mv 20－e ＝3mv 22e.【答案】 3mv 22e如图1­5所示，匀强电场的方向沿x 轴的正方向，场强为E .在A (l,0)点有一个质量为m 、电荷量为q 的粒子，以沿y 轴负方向的初速度v 0开始运动，经过一段时间到达B (0，－2l )点．不计重力作用，求：图1­5(1)粒子的初速度v 0的大小；(2)粒子到达B 点时的速度v 的大小及方向． 【解析】 (1)粒子在y 轴方向做匀速直线运动： 2l ＝v 0t粒子在x 轴方向做匀加速直线运动：l ＝12at 2又a ＝qE m解得：t ＝2ml qEv 0＝2qElm.(2)x 方向分速度v x ＝at ＝2qElm到达B 点时速度的大小v ＝v 2x ＋v 20＝2qElm速度与y 轴负方向的夹角 tan θ＝v x v 0＝1，则θ＝45°. 【答案】 (1)2qElm(2)2qElm与y 轴负方向的夹角为45°处理带电粒子在电场中运动的一般思路(1)分析带电粒子的受力情况，尤其要注意是否应该考虑重力，电场力是否为恒力等． (2)分析带电粒子的初始状态及条件，确定带电粒子做直线运动还是曲线运动． (3)建立正确的物理模型，进而确定解题方法是运动学还是功能关系． (4)利用物理规律或其他手段(如图线等)找出物体间的关系，建立方程组．1.关于静电场的等势面，下列说法正确的是( ) 【导学号：96322025】 A ．两个电势不同的等势面可能相交 B ．电场线与等势面处处相互垂直 C ．同一等势面上各点电场强度一定相等D ．将一负的试探电荷从电势较高的等势面移至电势较低的等势面，电场力做正功 【解析】 在静电场中，两个电势不同的等势面不会相交，选项A 错误；电场线与等势面一定相互垂直，选项B 正确；同一等势面上的电场强度可能相等，也可能不相等，选项C 错误；电场线总是由电势高的等势面指向电势低的等势面，移动负试探电荷时，电场力做负功，选项D 错误．【答案】 B2．如图1­6所示，两个不带电的导体A和B，用一对绝缘柱支持使它们彼此接触．把一带正电荷的物体C置于A附近，贴在A、B下部的金属箔都张开( )【导学号：96322026】图1­6A．此时A带正电，B带负电B．此时A电势低，B电势高C．移去C，贴在A、B下部的金属箔都闭合D．先把A和B分开，然后移去C，贴在A、B下部的金属箔都闭合【解析】带电体C靠近导体A、B时，A、B发生静电感应现象，使A端带负电，B端带正电，但A、B是一个等势体，选项A、B错误；移去带电体C后，A、B两端电荷中和，其下部的金属箔都闭合，选项C正确；若先将A、B分开，再移去带电体C，A、B上的电荷不能中和，其下部的金属箔仍张开，选项D错误．【答案】 C3.(多选)如图1­7，一带负电荷的油滴在匀强电场中运动，其轨迹在竖直面(纸面)内，且相对于过轨迹最低点P的竖直线对称．忽略空气阻力．由此可知( )【导学号：96322027】图1­7A．Q点的电势比P点高B．油滴在Q点的动能比它在P点的大C．油滴在Q点的电势能比它在P点的大D．油滴在Q点的加速度大小比它在P点的小【解析】带电油滴在电场中受重力、电场力作用，据其轨迹的对称性可知，电场力方向竖直向上，且电场力大于重力，电场力先做负功后做正功．则电场强度方向向下，Q点的电势比P点高，选项A正确；油滴在P点的速度最小，选项B正确；油滴在P点的电势能最大，选项C错误；油滴运动的加速度大小不变，选项D错误．【答案】AB4．如图1­8，直线a、b和c、d是处于匀强电场中的两组平行线，M、N、P、Q是它们的交点，四点处的电势分别为φM、φN、φP、φQ.一电子由M点分别运动到N点和P点的过程中，电场力所做的负功相等．则( )图1­8A．直线a位于某一等势面内，φM>φQB．直线c位于某一等势面内，φM>φNC．若电子由M点运动到Q点，电场力做正功D．若电子由P点运动到Q点，电场力做负功【解析】由电子从M点分别运动到N点和P点的过程中电场力所做的负功相等可知，N、P两点在同一等势面上，且电场线方向为M→N，故选项B正确，选项A错误．M点与Q 点在同一等势面上，电子由M点运动到Q点，电场力不做功，故选项C错误．电子由P点运动到Q点，电场力做正功，故选项D错误．【答案】 B5．一金属容器置于绝缘板上，带电小球用绝缘细线悬挂于容器中，容器内的电场线分布如图1­9所示，容器内表面为等势面，A、B为容器内表面上的两点，下列说法正确的是( ) 【导学号：96322028】图1­9A．A点的电场强度比B点的大B．小球表面的电势比容器内表面的低C．B点的电场强度方向与该处内表面垂直D．将检验电荷从A点沿不同路径移到B点，电场力所做的功不同【解析】由题图知，B点处的电场线比A点处的密，则A点的电场强度比B点的小，选项A错误；沿电场线方向电势降低，选项B错误；电场强度的方向总与等势面导体表面垂直，选项C正确；检验电荷由A点移动到B点，电场力做功一定，与路径无关，选项D错误．【答案】 C6．如图1­10所示，两平行的带电金属板水平放置．若在两板中间a点从静止释放一带电微粒，微粒恰好保持静止状态．现将两板绕过a点的轴(垂直于纸面)逆时针旋转45°，再由a点从静止释放一同样的微粒，该微粒将( ) 【导学号：96322029】图1­10A ．保持静止状态B ．向左上方做匀加速运动C ．向正下方做匀加速运动D ．向左下方做匀加速运动【解析】 两板水平放置时，放置于两板间a 点的带电微粒保持静止，带电微粒受到的电场力与重力平衡．当将两板逆时针旋转45°时，电场力大小不变，方向逆时针偏转45°，受力如图，则其合力方向沿二力角平分线方向，微粒将向左下方做匀加速运动．选项D 正确．【答案】 D7.如图1­11，P 是固定的点电荷，虚线是以P 为圆心的两个圆．带电粒子Q 在P 的电场中运动，运动轨迹与两圆在同一平面内，a 、b 、c 为轨迹上的三个点．若Q 仅受P 的电场力作用，其在a 、b 、c 点的加速度大小分别为a a 、a b 、a c ，速度大小分别为v a 、v b 、v c .则( ) 【导学号：96322030】图1­11A ．a a >a b >a c ，v a >v c >v bB ．a a >a b >a c ，v b >v c >v aC ．a b >a c >a a ，v b >v c >v aD ．a b >a c >a a ，v a >v c >v b【解析】 a 、b 、c 三点到固定的点电荷P 的距离r b <r c <r a ，则三点的电场强度由E ＝kQr 可知E b >E c >E a ，故带电粒子Q 在这三点的加速度a b >a c >a a .由运动轨迹可知带电粒子Q 所受P 的电场力为斥力，从a 到b 电场力做负功，由动能定理－|qU ab |＝12mv 2b －12mv 2a <0，则vb <v a ，从b 到c 电场力做正功，由动能定理|qU bc |＝12mv 2c －12mv 2b >0，vc >v b ，又|U ab |>|U bc |，则v a >v c ，故v a >v c >v b ，选项D 正确．【答案】 D8．如图1­12所示，一质量为m 、电荷量为q (q >0)的粒子在匀强电场中运动，A 、B 为其运动轨迹上的两点．已知该粒子在A 点的速度大小为v 0，方向与电场方向的夹角为60°；它运动到B 点时速度方向与电场方向的夹角为30°.不计重力．求A 、B 两点间的电势差. 【导学号：96322031】图1­12【解析】 设带电粒子在B 点的速度大小为v B .粒子在垂直于电场方向的速度分量不变，即v B sin 30°＝v 0sin 60°①由此得v B ＝3v 0②设A 、B 两点间的电势差为U AB ，由动能定理有qU AB ＝12m (v 2B －v 20)③联立②③式得U AB ＝mv 20q .【答案】 mv 20q章末综合测评(一) (时间：60分钟 满分：100分)一、选择题(本大题共10个小题，共60分．在每小题所给的四个选项中，第1～7题只有一项符合题目要求，第8～10题有多项符合题目要求，全部选对的得6分，选对但不全的得3分，有选错的得0分．)1．关于电场线的以下说法中正确的是( )【导学号：96322175】A ．电场线上每一点的切线方向都跟电荷在该点的受力方向相同B ．沿电场线的方向，电场强度越来越小C ．电场线越密的地方同一试探电荷所受的静电力就越大D ．顺着电场线移动电荷，电荷受静电力大小一定不变【解析】 电场线上每一点的切线方向都跟正电荷在该点的受力方向相同，故选项A 错误；沿电场线方向，其疏密变化情况未知，所以电场强度大小不能判定，电荷的受力情况也不能判定，故选项B 、D 错误；电场线越密的地方同一试探电荷所受的静电力就越大，故选项C 正确．【答案】 C2．真空中，A 、B 两点与点电荷Q 的距离分别为r 和3r ，则A 、B 两点的电场强度大小之比为( )【导学号：96322176】A ．3∶1B ．1∶3C ．9∶1D ．1∶9【解析】 由点电荷场强公式有：E ＝k Q r2∝r －2，故有E A E B ＝⎝ ⎛⎭⎪⎫r B r A 2＝⎝ ⎛⎭⎪⎫3r r2＝9∶1，C 项正确．【答案】 C3．下列选项中的各14圆环大小相同，所带电荷量已在图中标出，且电荷均匀分布，各14圆环间彼此绝缘．坐标原点O 处电场强度最大的是( )【解析】 由对称性原理可知，A 、C 图中O 点的场强大小相等，D 图中O 点场强为0，因此B 图中两14圆环在O 点处合场强应最大，选项B 正确．【答案】 B4．如图1所示，O 为两个等量异种电荷连线的中点，P 为连线中垂线上的一点，比较O 、P 两点的电势和场强大小( )A．φO＝φP，E O＞E PB．φO＝φP，E O＝E PC．φO＞φP，E O＝E PD．φO＝φP，E O＜E P【解析】根据等量异种电荷电场的分布情况可知，中垂线是等势线，故φO＝φP，根据电场线的疏密知，E O>E P，故A项正确．【答案】 A5．如图2所示，一带电粒子在电场中沿曲线AB运动，从B点穿出电场，a、b、c、d 为该电场中的等势面，这些等势面都是互相平行的竖直平面，不计粒子所受重力，则( ) 【导学号：96322177】图2A．该粒子一定带负电B．此电场不一定是匀强电场C．该电场的电场线方向一定水平向左D．粒子在电场中运动过程动能不断减少【解析】由于不能确定电场线方向，故不能确定粒子带负电，A、C错误．等势面互相平行，故一定是匀强电场，B错误．粒子受电场力一定沿电场线指向轨迹凹侧，而电场线和等势面垂直，由此可确定电场力一定做负功，故动能不断减少，D正确．【答案】 D6．如图3所示，B、D在以点电荷＋Q为圆心的圆上，B、C在以QB连线中点为圆心的圆上，将一检验电荷从A点分别移到B、C、D各点时，电场力做功是( )A ．W AB ＝W AC B ．W AD ＞W AB C ．W AC ＞W ADD ．W AB ＝W AD【解析】 由题图可知，B 、D 在同一个等势面上，C 点的电势比B 点高，所以从A 点向B 、C 、D 三点移动电荷时，移至B 、D 两点电场力做功是一样多的，移至C 点时电场力做功比移至B 、D 点少．【答案】 D7．如图4所示，a 、b 两个带正电的粒子，以相同的速度先后垂直于电场线从同一点进入平行板间的匀强电场后，a 粒子打在B 板的a ′点，b 粒子打在B 板的b ′点，若不计重力，则( ) 【导学号：96322178】图4A ．a 的电荷量一定大于b 的电荷量B ．b 的质量一定大于a 的质量C ．a 的比荷一定大于b 的比荷D ．b 的比荷一定大于a 的比荷【解析】 据题意，带电粒子在匀强电场中做类平抛运动，其水平位移为：x ＝vt ，竖直位移为：y ＝12at 2＝12qE mt 2，当a 、b 以相同速度垂直电场线进入电场后，有：x ＝v2myqE ，由于v 、y 和E 都相等，而b 粒子的水平位移大，故b 粒子的m q较大，因而a 粒子的qm较大，故C 选项正确．【答案】 C8．一带电粒子在正电荷形成的电场中，运动轨迹如图5所示的abcd 曲线，下列判断正确的是( )【导学号：96322179】图5A ．粒子带正电B ．粒子通过a 点时的速度比通过b 点时小C ．粒子在a 点受到的静电力比b 点小D ．粒子在a 点时的电势能与在d 点相等【解析】 根据同种电荷相互排斥，异种电荷相互吸引，可知粒子带正电荷，故选项A 正确；从a 向b 运动过程中，斥力做负功，因此动能减小，速度减小，故选项B 错误；根据库仑定律F ＝kq 1q 2r 2可知，在a 点两个电荷间距离远，受静电力小，故选项C 正确；粒子在a 点与在d 点处于同一等势面上，从a 到d 的过程中，静电力不做功，因此电势能相等，故选项D 正确．【答案】 ACD9．如图6所示，两块平行金属板正对着水平放置，两板分别与电源正、负极相连．当开关闭合时，一带电液滴恰好静止在两板间的M 点．则()图6A ．当开关闭合时，若减小两板间距，液滴仍静止B ．当开关闭合时，若增大两板间距，液滴将下降C ．开关再断开后，若减小两板间距，液滴仍静止D ．开关再断开后，若增大两板间距，液滴将下降【解析】 当开关闭合时，电容器两端电压为定值，等于电源电压，设为U ，两板间的距离为d ，带电液滴处于平衡状态，则mg ＝q U d，当两板间的距离减小时，所受电场力大于重力，液滴将向上做匀加速运动，A 错误；两板间的距离增大时，所受电场力小于重力，液滴将向下做匀加速运动，B 正确；当开关断开后，电容器无法放电，两板间的电荷量不变，设为Q ，此时两板间的场强大小E ＝U d ＝Q C d ∝QεS，可见场强大小与两板间距离无关，即场强大小保持不变，电场力不变，液滴保持静止，C 正确，D 错误．【答案】 BC10．如图7所示，A 、B 、C 、D 是匀强电场中的四个点，D 是BC 的中点，A 、B 、C 构成一直角三角形，AB ＝L m ，电场线与三角形所在的平面平行，已知A 点的电势为5 V ，B 点的电势为－5 V ，C 点的电势为15 V ，据此可以判断( ) 【导学号：96322180】图7A ．场强方向由C 指向B B ．场强方向垂直AD 连线指向BC ．场强大小为10LV/mD ．场强大小为203LV/m【解析】 根据B 、C 点的电势可以确定其中点D 的电势为5 V ，A 、D 的连线为一条等势线，电场线与等势面垂直，且由高等势面指向低等势面，故场强方向垂直AD 连线指向B ，A 错误，B 正确；匀强电场的场强E ＝U AB d ，其中U AB ＝10 V ，d ＝L cos 30°，解得E ＝203LV/m ，C 错误，D 正确．【答案】 BD二、计算题(本大题共3个小题，共40分．按题目要求作答．)11．(12分)如图8所示，在真空中的O 点放一点电荷Q ＝1.0×10－9C ，直线MN 过O 点，OM ＝30 cm ，M 点放一点电荷q ＝－2×10－10 C ，求：图8(1)M 点的场强大小；(2)若M 点的电势比N 点的电势高15 V ，则电荷q 从M 点移到N 点，它的电势能变化了多少？【解析】 (1)根据E ＝kQ r2得M 点的场强 E ＝9.0×109× 1.0×10－930×10－22 N/C ＝100 N/C.(2)电荷q 从M 点移到N 点，电场力做功W MN ＝qU MN ＝－2×10－10×15 J＝－3×10－9 J.这一过程中电场力做负功，电势能增加3×10－9J. 【答案】 (1)100 N/C (2)电势能增加了3×10－9 J12．(12分)如图9所示，在水平方向的匀强电场中，用长为L 的绝缘细线拴住一质量为m 、电荷量为q 的小球，线的上端固定，开始时连线拉成水平，突然松开后，小球由静止开始向下摆动，当细线转过60°角时的速度恰好为零．求：【导学号：96322181】图9(1)A 、B 两点的电势差U AB 为多大？ (2)电场强度为多大？【解析】 (1)取带电小球为研究对象，由动能定理得mgL sin 60°＋qU AB ＝0，故U AB ＝－3mgL2q. (2)由E ＝U d 得电场强度为E ＝－U AB L 1－cos 60° ＝3mgq.【答案】 (1)－3mgL 2q (2)3mg q13．(16分)如图10所示，一质量m ＝5×10－3kg(忽略重力)的微粒带正电，其电荷量为q ＝1×10－4C ．从距上极板5 cm 处以2 m/s 的水平初速度进入长为20 cm 、板间距也为20 cm 的两极板间，如果两极板不带电，微粒将运动到距极板最右端10 cm 的竖直荧光屏上的O 点．现将两极板间加200 V 的电压，带电微粒打到荧光屏上的A 点．图10(1)带电微粒从进入电场到到达荧光屏上的A 点所经历的时间为多少？ (2)OA 两点的间距为多少？(3)带电微粒进入电场到打到荧光屏上的A 点这一过程中电场力对其做功多少？ 【解析】 (1)设板长为l 1，极板最右端到荧光屏的距离为l 2，微粒初速度为v ，由于带电微粒在水平方向上的速度始终不变，则t ＝l 1＋l 2v ＝0.2＋0.12s ＝0.15 s. (2)设微粒在两极板间的偏转位移为y ，则y ＝12at 2＝qUl 212mdv 2＝1×10－4×200× 0.222×5×10－3×0.2×22 m ＝0.1 m. 在类平抛运动中，利用速度的反向延长线交于水平位移的中点．再根据三角形相似，求得OA 长为0.2 m.(3)W ＝qEy ＝qUy d ＝1×10－4×200×0.10.2J ＝0.01 J.【答案】 (1)0.15 s (2)0.2 m (3)0.01 J2.磁场对通电导线的作用——安培力[先填空]1．安培力磁场对通电导线的作用力．2．科学探究：安培力与哪些因素有关(1)实验探究采用的方法：控制变量法．(2)当通电导线与磁感线垂直时，实验结论是：①当其他因素不变，磁感应强度增大时，安培力增大；②当其他因素不变，电流增大时，安培力增大；③当其他因素不变，导体长度增大时，安培力增大；④安培力的方向由磁场方向和电流方向共同决定．3．安培力的大小(1)F＝ILB.(2)适用条件①通电导线与磁场方向垂直．②匀强磁场或非匀强磁场中很短的导体．[再判断]1．通电导体在磁场中所受安培力为零，该处磁场感应强度一定为零．(×)2．两根通电导线在同一匀强磁场中，若导线长度相同，电流大小相等，则所受安培力大小相等，方向相同．(×)3．通以10 A电流的直导线，长为0.1 m，处在磁感应强度为0.1 T的匀强磁场中，所受安培力可能为0.02 N．(√)[后思考]通电导体在磁场中所受安培力F的大小一定等于ILB吗？【提示】不一定．只有当通电导体中的电流方向与磁场方向垂直时，安培力F才等于ILB.[合作探讨]如3­2­1所示，利用下列实验装置可以探究安培力的大小与磁场、电流大小的关系．(1)在B、L一定时，增大电流I，导线受力怎么变化？(2)在B、I一定时，增大导线的长度L，导线受力怎么变化？3­2­1【提示】(1)当B、L一定时，增大电流I、导线受的力变大．(2)当B、I一定时，增大导线长度L导线受力变大．[核心点击]1．当电流方向与磁场方向垂直时，F＝ILB.此时通电导线所受安培力最大．2．当电流方向与磁场方向不垂直时，F＝ILB sin θ(θ是I和B之间的夹角)．3．当通电导线的方向和磁场方向平行(θ＝0°或θ＝180°)时，安培力最小，等于零．4．若导线是弯曲的，公式中的L并不是导线的总长度，而应是弯曲导线的“有效长度”．它等于连接导线两端点直线的长度(如图3­2­2所示)，相应的电流方向沿两端点连线由始端流向末端．图3­2­2一根长为0.2 m、电流为2 A的通电导线，放在磁感应强度为0.5 T的匀强磁场中，受到的安培力大小不可能是( )A．0.4 N B．0.2 NC．0.1 N D．0【解析】由安培力的公式F＝ILB sin θ可知，安培力的大小与I和B的夹角有关．当θ＝90°时，F 最大，F max ＝ILB ＝2×0.2×0.5 N＝0.2 N ．当θ＝0°时，F 最小，F min ＝0，故F 的大小范围是0≤F ≤0.2 N，故B 、C 、D 可能，A 不可能．【答案】 A如图3­2­3所示，导线框中电流为I ，导线框垂直于磁场放置，磁感应强度为B ，AB 与CD 相距为d ，则MN 所受安培力大小为( )【导学号：96322061】图3­2­3A ．F ＝BIdB ．F ＝BId sin θC ．F ＝BIdsin θD ．F ＝BId cos θ【解析】 导线与B 垂直，F ＝BI dsin θ.【答案】 C如图所示，在匀强磁场中放有下列各种形状的通电导线，电流均为I ，磁感应强度均为B ，求各导线所受到的安培力的大小．【解析】 A 图中，F ＝IlB cos α，这时不能死记公式而错写成F ＝IlB sin α.要理解公式本质是有效长度或有效磁场，正确分解．B 图中，B ⊥I ，导线在纸平面内，故F ＝IlB .C 图是两根导线组成的折线abc ，整体受力实质上是两部分直导线分别受力的矢量和，其有效长度为ac ，故F ＝2IlB .D 图中，从a →b 的半圆形电流，分析圆弧上对称的每一小段电流，受力抵消合并后，其有效长度为ab ，故F ＝2IRB .E 图中，F ＝0.【答案】 A ：IlB cos α B ：IlB C ：2IlB D ：2IRB E ：0计算安培力大小应注意的问题(1)应用公式F ＝IlB ，电流方向必须与磁场方向垂直．(2)通电导线放入磁场中，有可能不受安培力的作用．(3)公式F ＝IlB 中的l 不一定是导线的实际长度，而应是“有效长度”．[先填空]1．安培力的方向(1)左手定则：伸出左手，四指并拢，使大拇指和其余四指垂直，并且都跟手掌在同一平面内，让磁感线垂直穿过手心，四指指向沿电流方向，则大拇指所指方向就是通电导线所受安培力的方向．(2)方向特点：安培力的方向既与电流方向垂直，又与磁场方向垂直，即安培力方向垂直于电流方向和磁场方向所确定的平面．2．电动机(1)原理：利用磁场对通电线圈的安培力使线圈在磁场中旋转．(2)作用：把电能转化为机械能．(3)分类⎩⎪⎨⎪⎧ 直流电动机：由磁场、转动线圈、滑环、电刷 及电源组成，滑环在其中起了一个换向器 的作用. 交流电动机：如家用电风扇、洗衣机、抽油烟 机等都是交流电动机.[再判断] 1．当通电直导线垂直于磁场方向时，安培力的方向和磁场方向相同．(×)2．磁感应强度的方向与安培力的方向垂直．(√)3．电动机是把电能转化为机械能的装置．(√)[后思考]通电直导线在磁场中所受安培力的方向一定跟电流的方向垂直吗？【提示】 一定．根据左手定则可判断安培力的方向垂直于电流和磁场方向．[合作探讨]如图3­2­4所示，利用下列装置可以探究安培力的方向与磁场、电流方向的关系．(1)图中磁场方向向哪？闭合电键后，导线中电流方向向哪？。

逻辑学题型一、填空题（约10分）二、名词解释（或定义题）（约10分）三、简答题（约10分）四、分析题（约50分）（要根据题目要求从概念、推理、基本规律等角度对某句话或某段话进行分析。

）五、证明题（约10分）六、推理运用题（约10分）逻辑学复习提纲第一章绪论第二章概念1、明确概念的定义2明确概念和语词的关系3熟练掌握概念的内涵和外延4区分集合概念和非集合概念(仅内招生掌握)5会识别概念之间的关系，能用欧拉图解表示6熟练掌握实质定义的方法和定义的规则7会分析概念表述方面出现错误（1）属种关系概念并列使用(2)交叉关系概念并列使用(3)定义错误(4)划分错误(5)误用集合概念(仅内招生掌握)第三章简单判断及其推理1、了解判断的定义及其逻辑特征2、掌握推理的定义和分类3、熟练掌握直言判断的对当关系4、熟练掌握直言判断项的周延性(仅内招生掌握)5、掌握换质法的公式（4个）6、熟练掌握换位法的规则和公式（3个）第四章复合判断及其推理1、掌握以下几个概念（1）联言判断和联言推理（2）选言判断和选言推理（3）假言判断和假言推理（4）充分条件（5）必要条件（6）充要条件2、熟练掌握6个真值表3、熟练掌握相容选言推理、不相容选言推理的公式和规则（3个公式）4、熟练掌握充分条件假言推理、必要条件假言推理的公式和规则（4个公式）5、掌握二难推理的特征和破斥方法(仅内招生掌握)第五章语用逻辑初步1、能指出一个话语的预设和话涵能2给出一个问句的回避和回绝3掌握预设的种类(仅内招生掌握)4熟练掌握Grice的会话合作原则5熟练掌握话涵的产生机制掌握话涵的运用第六章基本规律1、熟练掌握同一律、矛盾律和排中律的基本内容2会识别和分析违反三条规律的逻辑错误第七章论证1、掌握论证（论辩）的规则2、熟练掌握反证法和归谬法反证法：通过确定与论题相矛盾的命题的虚假来确定原论题的真实性。

证明：p思路：假定p不成立，即¬p¬p q ( q为明显的错误)¬q¬¬p( 即p)根据排中律，¬ p为假，则p不能为假，即p为真归谬法：通过确定被反驳论题的荒谬性来反驳对方。

立体几何问题重在“建”——建模、建系[思维流程——找突破口] [技法指导——迁移搭桥] 立体几何解答题建模、建系策略 立体几何解答题的基本模式是论证推理与计算相结合，以某个几何体为依托，分步设问，逐层加深．解决这类题目的原则是建模、建系．建模——将问题转化为平行模型、垂直模型、平面化模型及角度、距离等的计算模型．建系——依托于题中的垂直条件，建立空间直角坐标系，利用空间向量求解.[典例] (2018·全国卷Ⅱ)如图，在三棱锥P ­ABC 中，AB ＝BC ＝22，PA ＝PB ＝PC ＝AC ＝4，O 为AC 的中点．(1)证明：PO ⊥平面ABC ；(2)若点M 在棱BC 上，且二面角M ­PA ­C 为30°，求PC 与平面PAM 所成角的正弦值．[快审题]求什么想什么证明线面垂直，想线面垂直成立的条件． 求线面角的正弦值，想平面的法向量及直线的方向向量． 给什么用什么给出边的长度，用勾股定理证线线垂直． 给出二面角的大小，可求出点M 的位置． 差什么找什么差点M 的坐标，利用垂直关系建立空间直角坐标系，找出平面PAM ，平面PAC 的法向量.[稳解题](1)证明：因为PA ＝PC ＝AC ＝4，O 为AC 的中点，所以PO ⊥AC ，且PO ＝2 3.连接OB ，因为AB ＝BC ＝22AC ， 所以△ABC 为等腰直角三角形，且OB ⊥AC ，OB ＝12AC ＝2.所以PO 2＋OB 2＝PB 2， 所以PO ⊥OB . 又因为OB ∩AC ＝O ， 所以PO ⊥平面ABC . (2)以O 为坐标原点， OB ―→的方向为x 轴正方向，建立如图所示的空间直角坐标系O ­xyz .由已知得O (0,0,0)，B (2,0,0)， A (0，－2,0)，C (0,2,0)，P (0,0,23)，AP ―→＝(0,2,23)．取平面PAC 的一个法向量OB ―→＝(2,0,0)．设M (a,2－a,0)(0<a ≤2)，则AM ―→＝(a,4－a,0)．设平面PAM 的法向量为n ＝(x ，y ，z )．由⎩⎪⎨⎪⎧ AP ―→·n ＝0，AM ―→·n ＝0，得⎩⎨⎧ 2y ＋23z ＝0，ax ＋4－a y ＝0，令y ＝3a ，得z ＝－a ，x ＝3(a －4)，所以平面PAM 的一个法向量为n ＝(3(a －4)，3a ，－a )，所以cos 〈OB ―→，n 〉＝23a －423a －42＋3a 2＋a2. 由已知可得|cos 〈OB ―→，n 〉|＝cos 30°＝32， 所以23|a －4|23a －42＋3a 2＋a 2＝32， 解得a ＝43或a ＝－4(舍去)． 所以n ＝⎝ ⎛⎭⎪⎫－833，433，－43. 又PC ―→＝(0,2，－23)，所以cos 〈PC ―→，n 〉＝833＋8334＋12·643＋163＋169＝34.所以PC与平面PAM所成角的正弦值为34.[题后悟道] 利用法向量求解空间角的关键在于“四破”[针对训练](2018·惠州第二次调研)如图，在四棱锥P­ABCD中，底面ABCD是边长为2的菱形，∠ABC＝60°，PA⊥PB，PC＝2.(1)求证：平面PAB⊥平面ABCD；(2)若PA＝PB，求二面角A­PC­D的余弦值．解：(1)证明：取AB的中点O，连接CO，PO，∵四边形ABCD是边长为2的菱形，∴AB＝BC＝2.∵∠ABC＝60°，∴△ABC是等边三角形，∴CO⊥AB，OC＝ 3.∵PA⊥PB，∴PO＝12AB＝1.∵PC＝2，∴OP2＋OC2＝PC2，∴CO⊥PO.∵AB∩PO＝O，∴CO⊥平面PAB.∵CO⊂平面ABCD，∴平面PAB⊥平面ABCD.(2)∵PA＝PB，∴PO⊥AO.由(1)知，平面PAB⊥平面ABCD，∴PO⊥平面ABCD，∴直线OC，OB，OP两两垂直．以O为坐标原点建立如图所示的空间直角坐标系O­xyz.则O(0,0,0)，A(0，－1,0)，C(3，0,0)，D(3，－2,0)，P(0，0,1)．∴AP―→＝(0,1,1)，PC―→＝(3，0，－1)，DC―→＝(0,2,0)．设平面APC 的法向量为m ＝(x 1，y 1，z 1)，由⎩⎪⎨⎪⎧m ·AP ―→＝0，m ·PC ―→＝0，得⎩⎨⎧ y 1＋z 1＝0，3x 1－z 1＝0， 取x 1＝1，得m ＝(1，－3，3)为平面APC 的一个法向量， 设平面PCD 的法向量为n ＝(x 2，y 2，z 2)，由⎩⎪⎨⎪⎧ n ·PC ―→＝0，n ·DC ―→＝0，得⎩⎨⎧ 3x 2－z 2＝0，2y 2＝0，取x 2＝1，得n ＝(1,0，3)为平面PCD 的一个法向量，∴cos 〈m ，n 〉＝m ·n | m |·| n |＝277， 由图知，二面角A ­PC ­D 为锐二面角，∴二面角A ­PC ­D 的余弦值为277.[专题过关检测]A 组——大题考点落实练1.如图，在四棱柱ABCD ­A 1B 1C 1D 1中，A 1A ⊥底面ABCD ，四边形ABCD为菱形，A 1A ＝AB ＝2，∠ABC ＝60°，E ，F 分别是BC ，A 1C 的中点．(1)求异面直线EF ，AD 所成角的余弦值；(2)点M 在线段A 1D 上，A 1M A 1D＝λ，若CM ∥平面AEF ，求实数λ的值．解：(1)因为A 1A ⊥平面ABCD ，AE ⊂平面ABCD ，AD ⊂平面ABCD ，所以A 1A ⊥AE ，A 1A ⊥AD .在菱形ABCD 中，∠ABC ＝60°，连接AC ，则△ABC 是等边三角形．因为E 是BC 的中点，所以BC ⊥AE .因为BC ∥AD ，所以AE ⊥AD .以A 为坐标原点，AE 为x 轴，AD 为y 轴，AA 1为z 轴建立如图所示的空间直角坐标系，则A (0,0，0)，C (3，1,0)，D (0,2,0)，A 1(0,0,2)，E (3，0,0)，F ⎝⎛⎭⎪⎫32，12，1，AD ―→＝(0,2,0)，EF ―→＝⎝ ⎛⎭⎪⎫－32，12，1， 所以cos 〈AD ―→，EF ―→〉＝AD ―→·EF ―→|AD ―→|·|EF ―→|＝122＝24， 所以异面直线EF ，AD 所成角的余弦值为24. (2)设M (x ，y ，z )，由于点M 在线段A 1D 上，且A 1M A 1D＝λ， 所以A 1M ―→＝λA 1D ―→，则(x ，y ，z －2)＝λ(0,2，－2)．解得M (0,2λ，2－2λ)，所以CM ―→＝(－3，2λ－1,2－2λ)．设平面AEF 的一个法向量为n ＝(x 0，y 0，z 0)．因为AE ―→＝(3，0,0)，AF ―→＝⎝ ⎛⎭⎪⎫32，12，1， 所以⎩⎪⎨⎪⎧ AE ―→·n ＝0， AF ―→·n ＝0，即⎩⎪⎨⎪⎧ 3x 0＝0，32x 0＋12y 0＋z 0＝0，取y 0＝2，得z 0＝－1，则平面AEF 的一个法向量为n ＝(0,2，－1)．由于CM ∥平面AEF ，则n ·CM ―→＝0，即2(2λ－1)－(2－2λ)＝0，解得λ＝23. 2.(2019届高三·河北三市联考)如图，三棱柱ADE ­BCG 中，四边形ABCD 是矩形，F 是EG 的中点，EA ⊥AB ，AD ＝AE ＝EF ＝1，平面ABGE⊥平面ABCD .(1)求证：AF ⊥平面FBC ；(2)求二面角B ­FC ­D 的正弦值．解：(1)证明：∵四边形ABCD 是矩形，∴BC ⊥AB ，又平面ABGE ⊥平面ABCD ，∴BC ⊥平面ABGE ，∵AF ⊂平面ABGE ，∴BC ⊥AF .在△AFB 中，AF ＝BF ＝2，AB ＝2， ∴AF 2＋BF 2＝AB 2，即AF ⊥BF ，又BF ∩BC ＝B ，∴AF ⊥平面FBC .(2)分别以AD ，AB ，AE 所在直线为x 轴，y 轴，z 轴建立空间直角坐标系，则A (0,0,0)，D (1,0,0)，C (1,2,0)，E (0,0,1)，B (0,2,0)，F (0,1,1)，∴DE ―→＝(－1,0,1)，DC ―→＝(0,2,0)，设n 1＝(x ，y ，z )为平面CDEF 的法向量，则⎩⎪⎨⎪⎧ n 1·DC ―→＝0，n 1·DE ―→＝0，即⎩⎪⎨⎪⎧ 2y ＝0，－x ＋z ＝0，令x ＝1，得z ＝1，即n 1＝(1,0,1)为平面CDEF 的一个法向量，取n 2＝AF ―→＝(0,1,1)为平面BCF 的一个法向量，∴cos 〈n 1，n 2〉＝n 1·n 2| n 1|| n 2|＝12， ∴二面角B ­FC ­D 的正弦值为32. 3．如图，在四棱锥E ­ABCD 中，底面ABCD 为直角梯形，其中CD ∥AB ，BC ⊥AB ，侧面ABE ⊥平面ABCD ，且AB ＝AE ＝BE ＝2BC ＝2CD ＝2，动点F 在棱AE 上，且EF ＝λFA .(1)试探究λ的值，使CE ∥平面BDF ，并给予证明；(2)当λ＝1时，求直线CE 与平面BDF 所成角的正弦值．解：(1)当λ＝12时，CE ∥平面BDF .证明如下： 连接AC 交BD 于点G ，连接GF ，∵CD ∥AB ，AB ＝2CD ，∴CG GA ＝CD AB ＝12， ∵EF ＝12FA ，∴EF FA ＝CG GA ＝12，∴GF ∥CE ， 又CE ⊄平面BDF ，GF ⊂平面BDF ，∴CE ∥平面BDF .(2)取AB 的中点O ，连接EO ，则EO ⊥AB ，∵平面ABE ⊥平面ABCD ，平面ABE ∩平面ABCD ＝AB ，∴EO ⊥平面ABCD ，连接DO ，∵BO ∥CD ，且BO ＝CD ＝1，∴四边形BODC 为平行四边形，∴BC ∥DO ，又BC ⊥AB ，∴AB ⊥OD ，则OD ，OA ，OE 两两垂直，以O 为坐标原点，OD ，OA ，OE 所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系O ­xyz ，则O (0,0,0)，A (0,1,0)，B (0，－1,0)，D (1,0,0)，C (1，－1，0)，E (0,0，3)． 当λ＝1时，有EF ―→＝FA ―→，∴F ⎝ ⎛⎭⎪⎫0，12，32， ∴BD ―→＝(1,1,0)，BF ―→＝⎝ ⎛⎭⎪⎫0，32，32，CE ―→＝(－1,1，3)． 设平面BDF 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ n ·BD ―→＝0，n ·BF ―→＝0，即⎩⎪⎨⎪⎧ x ＋y ＝0，32y ＋32z ＝0，令z ＝3，得y ＝－1，x ＝1，则n ＝(1，－1，3)为平面BDF 的一个法向量，设直线CE 与平面BDF 所成的角为θ，则sin θ＝|cos 〈CE ―→，n 〉|＝|－1－1＋3|5×5＝15， 故直线CE 与平面BDF 所成角的正弦值为15. 4．(2018·成都一诊)如图①，在边长为5的菱形ABCD 中，AC ＝6，现沿对角线AC 把△ADC 翻折到△APC 的位置得到四面体P ­ABC ，如图②所示．已知PB ＝4 2.(1)求证：平面PAC ⊥平面ABC ；(2)若Q 是线段AP 上的点，且A Q ―→＝13AP ―→，求二面角Q ­BC ­A 的余弦值．解：(1)证明：取AC 的中点O ，连接PO ，BO .∵四边形ABCD 是菱形，∴PA ＝PC ，PO ⊥AC .∵DC ＝5，AC ＝6，∴OC ＝3，PO ＝OB ＝4，∵PB ＝42， ∴PO 2＋OB 2＝PB 2，∴PO ⊥OB .∵OB ∩AC ＝O ，∴PO ⊥平面ABC .∵PO ⊂平面PAC ，∴平面PAC ⊥平面ABC .(2)∵AB ＝BC ，∴BO ⊥AC .故OB ，OC ，OP 两两垂直．以O 为坐标原点，OB ，OC ，OP 所在直线分别为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系O ­xyz .则B (4,0,0)，C (0,3,0)，P (0,0,4)，A (0，－3,0)．设点Q(x ，y ，z )．由A Q ―→＝13AP ―→，得Q ⎝⎛⎭⎪⎫0，－2，43. ∴BC ―→＝(－4,3,0)，B Q ―→＝⎝⎛⎭⎪⎫－4，－2，43. 设n 1＝(x 1，y 1，z 1)为平面BC Q 的法向量，由⎩⎪⎨⎪⎧ n 1·BC ―→＝0，n 1·B Q ―→＝0，得⎩⎪⎨⎪⎧ －4x 1＋3y 1＝0，－4x 1－2y 1＋43z 1＝0，取x 1＝3，则n 1＝(3,4,15)．取平面ABC 的一个法向量n 2＝(0,0,1)．∴cos 〈n 1，n 2〉＝n 1·n 2|n 1||n 2|＝1532＋42＋152＝31010， ∵二面角Q ­BC ­A 为锐角，∴二面角Q ­BC ­A 的余弦值为31010. B 组——大题专攻补短练1.在三棱锥P ­ABC 中，PA ＝PB ＝PC ＝2，BC ＝1，AC ＝3，AC ⊥BC . (1)求点B 到平面PAC 的距离． (2)求异面直线PA 与BC 所成角的余弦值． 解：(1)以C 为坐标原点，CA 为x 轴，CB 为y 轴，过C 作平面ABC 的垂线为z 轴，建立空间直角坐标系，取AB 的中点D ，连接PD ，DC ，因为△ACB 为直角三角形且AC ＝3，BC ＝1，所以AB ＝2，所以△PAB 为正三角形，所以PD ⊥AB 且PD ＝ 3.在△PDC 中，PC ＝2，PD ＝3，DC ＝1，所以PC 2＝PD 2＋DC 2，所以PD ⊥DC ，又AB ∩DC ＝D ，所以PD ⊥平面ABC .则A (3，0,0)，B (0,1,0)，D ⎝ ⎛⎭⎪⎫32，12，0，P ⎝ ⎛⎭⎪⎫32，12，3，C (0,0,0)，CA ―→＝(3，0,0)，CD ―→＝⎝ ⎛⎭⎪⎫32，12，0，CP ―→＝⎝ ⎛⎭⎪⎫32，12，3，CB ―→＝(0,1,0)， 设平面PAC 的法向量n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ n ·CA ―→＝0，n ·CP ―→＝0，即⎩⎪⎨⎪⎧ 3x ＝0，32x ＋12y ＋3z ＝0，取y ＝23，得n ＝(0,23，－1)为平面PAC 的一个法向量，所以点B 到平面PAC 的距离d ＝|CB ―→·n ||n |＝2313＝23913. (2)因为PA ―→＝⎝ ⎛⎭⎪⎫32，－12，－3，BC ―→＝(0，－1,0)， 设异面直线PA 与BC 所成角为θ，则cos θ＝|PA ―→·BC ―→||PA ―→|·|BC ―→|＝124×1＝14. 所以异面直线PA 与BC 所成角的余弦值为14.2.已知四棱锥P ­ABCD 中，底面ABCD 是梯形，BC ∥AD ，AB ⊥AD ，且AB ＝BC ＝1，AD ＝2，顶点P 在平面ABCD 内的射影H 在AD 上，PA ⊥PD .(1)求证：平面PAB ⊥平面PAD ；(2)若直线AC 与PD 所成角为60°，求二面角A ­PC ­D 的余弦值．解：(1)证明：∵PH ⊥平面ABCD ，AB ⊂平面ABCD ，∴PH ⊥AB .∵AB ⊥AD ，AD ∩PH ＝H ，AD ⊂平面PAD ，PH ⊂平面PAD ，∴AB ⊥平面PAD .又AB ⊂平面PAB ，∴平面PAB ⊥平面PAD .(2)以A 为坐标原点，建立如图所示的空间直角坐标系A ­xyz ，∵PH ⊥平面ABCD ，∴z 轴∥PH .则A (0,0,0)，C (1,1,0)，D (0,2,0)，设AH ＝a ，PH ＝h (0<a <2，h >0)． 则P (0，a ，h )．∴AP ―→＝(0，a ，h )，DP ―→＝(0，a －2，h )，AC ―→＝(1,1,0)．∵PA ⊥PD ，∴AP ―→·DP ―→＝a (a －2)＋h 2＝0.∵AC 与PD 所成角为60°，∴|cos 〈AC ―→，DP ―→〉|＝|a －2|2·a －22＋h 2＝12， ∴(a －2)2＝h 2，∴(a －2)(a －1)＝0，∵0<a <2，∴a ＝1.∵h >0，∴h ＝1，∴P (0,1,1)．∴AP ―→＝(0,1,1)，AC ―→＝(1,1,0)，PC ―→＝(1,0，－1)，DC ―→＝(1，－1,0)， 设平面APC 的法向量为n ＝(x 1，y 1，z 1)，则⎩⎪⎨⎪⎧n ·AP ―→＝0，n ·AC ―→＝0，即⎩⎪⎨⎪⎧ y 1＋z 1＝0，x 1＋y 1＝0， 令x 1＝1，得y 1＝－1，z 1＝1， ∴平面APC 的一个法向量为n ＝(1，－1,1)，设平面DPC 的法向量为m ＝(x 2，y 2，z 2)．则⎩⎪⎨⎪⎧ m ·PC ―→＝0，m ·DC ―→＝0，即⎩⎪⎨⎪⎧ x 2－z 2＝0，x 2－y 2＝0，令x 2＝1，得y 2＝1，z 2＝1，∴平面DPC 的一个法向量为m ＝(1,1,1)．∴cos 〈m ，n 〉＝m ·n |m ||n |＝13.∵二面角A ­PC ­D 的平面角为钝角， ∴二面角A ­PC ­D 的余弦值为－13.3．(2018·西安质检)如图，四棱柱ABCD ­A 1B 1C 1D 1的底面ABCD 是菱形，AC ∩BD ＝O ，A 1O ⊥底面ABCD ，AB ＝2，AA 1＝3.(1)证明：平面A 1CO ⊥平面BB 1D 1D ；(2)若∠BAD ＝60°，求二面角B ­OB 1­C 的余弦值． 解：(1)证明：∵A 1O ⊥平面ABCD ，BD ⊂平面ABCD . ∴A 1O ⊥BD .∵四边形ABCD 是菱形， ∴CO ⊥BD . ∵A 1O ∩CO ＝O ， ∴BD ⊥平面A 1CO . ∵BD ⊂平面BB 1D 1D ， ∴平面A 1CO ⊥平面BB 1D 1D .(2)∵A 1O ⊥平面ABCD ，CO ⊥BD ，∴OB ，OC ，OA 1两两垂直，以O 为坐标原点，OB ―→，OC ―→，OA 1―→的方向为x 轴，y 轴，z 轴的正方向建立如图所示的空间直角坐标系．∵AB ＝2，AA 1＝3，∠BAD ＝60°， ∴OB ＝OD ＝1，OA ＝OC ＝3，OA 1＝AA 21－OA 2＝ 6.则O (0,0,0)，B (1,0,0)，C (0，3，0)，A (0，－3，0)，A 1(0,0，6)， ∴OB ―→＝(1,0,0)，BB 1―→＝AA 1―→＝(0，3，6)， OB 1―→＝OB ―→＋BB 1―→＝(1，3，6)，OC ―→＝(0，3，0)． 设平面OBB 1的法向量为n ＝(x 1，y 1，z 1)， 则⎩⎪⎨⎪⎧ OB ―→·n ＝0，OB 1―→·n ＝0，即⎩⎨⎧x 1＝0，x 1＋3y 1＋6z 1＝0.令y 1＝2，得n ＝(0，2，－1)是平面OBB 1的一个法向量． 设平面OCB 1的法向量m ＝(x 2，y 2，z 2)， 则⎩⎪⎨⎪⎧OC ―→·m ＝0，OB 1―→·m ＝0，即⎩⎨⎧3y 2＝0，x 2＋3y 2＋6z 2＝0，令z 2＝－1，得m ＝(6，0，－1)为平面OCB 1的一个法向量，∴cos 〈n ，m 〉＝n ·m |n |·|m |＝13×7＝2121，由图可知二面角B ­OB 1­C 是锐二面角， ∴二面角B ­OB 1­C 的余弦值为2121. 4．(2018·潍坊统考)在平行四边形PABC 中，PA ＝4，PC ＝22，∠P ＝45°，D 是PA 的中点(如图1)．将△PCD 沿CD 折起到图2中△P 1CD 的位置，得到四棱锥P 1­ABCD .(1)将△PCD 沿CD 折起的过程中，CD ⊥平面P 1DA 是否成立？请证明你的结论． (2)若P 1D 与平面ABCD 所成的角为60°，且△P 1DA 为锐角三角形，求平面P 1AD 和平面P 1BC 所成角的余弦值．解：(1)将△PCD 沿CD 折起过程中，CD ⊥平面P 1DA 成立．证明如下： ∵D 是PA 的中点，PA ＝4，∴DP ＝DA ＝2， 在△PDC 中，由余弦定理得，CD 2＝PC 2＋PD 2－2PC ·PD ·cos 45°＝8＋4－2×22×2×22＝4， ∴CD ＝2＝PD ，∵CD 2＋DP 2＝8＝PC 2，∴△PDC 为等腰直角三角形且CD ⊥PA ， ∴CD ⊥DA ，CD ⊥P 1D ，P 1D ∩AD ＝D ， ∴CD ⊥平面P 1DA .(2)由(1)知CD ⊥平面P 1DA ，CD ⊂平面ABCD ， ∴平面P 1DA ⊥平面ABCD ，∵△P 1DA 为锐角三角形，∴P 1在平面ABCD 内的射影必在棱AD 上，记为O ，连接P 1O ，∴P 1O ⊥平面ABCD ，则∠P 1DA 是P 1D 与平面ABCD 所成的角， ∴∠P 1DA ＝60°， ∵DP 1＝DA ＝2，∴△P 1DA 为等边三角形，O 为AD 的中点，故以O 为坐标原点，过点O 且与CD 平行的直线为x 轴，DA 所在直线为y 轴，OP 1所在直线为z 轴建立如图所示的空间直角坐标系，设x 轴与BC 交于点M ， ∵DA ＝P 1A ＝2，∴OP 1＝3， 易知OD ＝OA ＝CM ＝1， ∴BM ＝3，则P 1(0,0，3)，D (0，－1,0)，C (2，－1,0)，B (2,3,0)，DC ―→＝(2,0,0)，BC ―→＝(0，－4,0)，P 1C ―→＝(2，－1，－3)，∵CD ⊥平面P 1DA ，∴可取平面P 1DA 的一个法向量n 1＝(1,0,0)， 设平面P 1BC 的法向量n 2＝(x 2，y 2，z 2)， 则⎩⎪⎨⎪⎧n 2·BC ―→＝0，n 2·P 1C ―→＝0，即⎩⎨⎧4y 2＝0，2x 2－y 2－3z 2＝0，令z 2＝1，则n 2＝⎝⎛⎭⎪⎫32，0，1， 设平面P 1AD 和平面P 1BC 所成的角为θ， 由图易知θ为锐角，∴cos θ＝|cos 〈n 1，n 2〉|＝|n 1·n 2|| n 1|·| n 2|＝321×72＝217.∴平面P 1AD 和平面P 1BC 所成角的余弦值为217.。

A B高考物理重要知识点总结学好物理要记住：最基本的知识、方法才是最重要的。

秘诀：“想” 学好物理重在理解．．．．．．．．（概念、规律的确切含义，能用不同的形式进行表达，理解其适用条件） A(成功)＝X(艰苦的劳动)十Y(正确的方法)十Z(少说空话多干实事)(最基础的概念,公式,定理,定律最重要)；每一题中要弄清楚(对象、条件、状态、过程)是解题关健物理学习的核心在于思维，只要同学们在平常的复习和做题时注意思考、注意总结、善于归纳整理，对于课堂上老师所讲的例题做到触类旁通，举一反三，把老师的知识和解题能力变成自己的知识和解题能力，并养成规范答题的习惯,这样，同学们一定就能笑傲考场，考出理想的成绩！对联: 概念、公式、定理、定律。

（学习物理必备基础知识） 对象、条件、状态、过程。

（解答物理题必须明确的内容）力学问题中的“过程”、“状态”的分析和建立及应用物理模型在物理学习中是至关重要的。

说明：凡矢量式中用“+”号都为合成符号，把矢量运算转化为代数运算的前提是先规定正方向。

答题技巧：“基础题，全做对；一般题，一分不浪费；尽力冲击较难题，即使做错不后悔”。

“容易题不丢分，难题不得零分。

“该得的分一分不丢，难得的分每分必争”，“会做⇒做对⇒不扣分”在学习物理概念和规律时不能只记结论，还须弄清其中的道理，知道物理概念和规律的由来。

力的种类:（13个力） 有18条定律、2条定理1重力： G = mg (g 随高度、纬度、不同星球上不同) 2弹力：F= Kx 3滑动摩擦力：F 滑= μN4静摩擦力： O ≤ f 静≤ f m (由运动趋势和平衡方程去判断)5浮力： F 浮= ρgV 排 6压力: F= PS = ρghs 7万有引力： F 引=G221r m m8库仑力： F=K221r q q (真空中、点电荷)9电场力： F 电=q E =qdu 10安培力：磁场对电流的作用力F= BIL (B ⊥I) 方向：左手定则11洛仑兹力：磁场对运动电荷的作用力f=BqV (B ⊥V) 方向：左手定则12分子力：分子间的引力和斥力同时存在,都随距离的增大而减小,随距离的减小而增大,但斥力变化得快．。

(名师选题)（精选试题附答案）高中数学选修一知识点归纳超级精简版单选题1、已知直线l 过定点A (2,3,1)，且方向向量为s ⃑=(0,1,1)，则点P (4,3,2)到l 的距离为（ ）A ．3√22B ．√22C ．√102D ．√2 答案：A分析：本题首先可根据题意得出AP ⃑⃑⃑⃑⃑⃑，然后求出|AP ⃑⃑⃑⃑⃑⃑|与|AP ⃑⃑⃑⃑⃑⃑⋅s ⃑|s ⃑||，最后根据空间点到直线的距离公式即可得出结果. 因为A (2,3,1)，P (4,3,2)，所以AP⃑⃑⃑⃑⃑⃑=(2,0,1)， 则|AP ⃑⃑⃑⃑⃑⃑|=√5，|AP ⃑⃑⃑⃑⃑⃑⋅s ⃑|s ⃑||=√22， 由点到直线的距离公式得d =√|AP ⃑⃑⃑⃑⃑⃑|2−|AP ⃑⃑⃑⃑⃑⃑⋅s ⃑|s ⃑||2=3√22， 故选：A.2、在正方体ABCD −A 1B 1C 1D 1中，P 为B 1D 1的中点，则直线PB 与AD 1所成的角为（ ）A ．π2B ．π3C ．π4D ．π6答案：D分析：平移直线AD 1至BC 1，将直线PB 与AD 1所成的角转化为PB 与BC 1所成的角，解三角形即可.如图，连接BC 1,PC 1,PB ，因为AD 1∥BC 1，所以∠PBC 1或其补角为直线PB 与AD 1所成的角，因为BB 1⊥平面A 1B 1C 1D 1，所以BB 1⊥PC 1，又PC 1⊥B 1D 1，BB 1∩B 1D 1=B 1，所以PC 1⊥平面PBB 1，所以PC 1⊥PB ，设正方体棱长为2，则BC 1=2√2,PC 1=12D 1B 1=√2，sin∠PBC 1=PC 1BC 1=12，所以∠PBC 1=π6.故选：D3、已知F 1,F 2是双曲线C 的两个焦点，P 为C 上一点，且∠F 1PF 2=60°,|PF 1|=3|PF 2|，则C 的离心率为（）A ．√72B ．√132C ．√7D ．√13答案：A分析：根据双曲线的定义及条件，表示出|PF 1|,|PF 2|，结合余弦定理可得答案.因为|PF 1|=3|PF 2|，由双曲线的定义可得|PF 1|−|PF 2|=2|PF 2|=2a ，所以|PF 2|=a ，|PF 1|=3a ；因为∠F 1PF 2=60°,由余弦定理可得4c 2=9a 2+a 2−2×3a ⋅a ⋅cos60°，整理可得4c 2=7a 2，所以e 2=c 2a 2=74，即e =√72.故选：A小提示：关键点睛：双曲线的定义是入手点，利用余弦定理建立a,c 间的等量关系是求解的关键.4、如图所示，在空间四边形OABC 中，OA ⃑⃑⃑⃑⃑⃑＝a ⃑,OB ⃑⃑⃑⃑⃑⃑=b ⃑⃑,OC ⃑⃑⃑⃑⃑⃑=c ⃑，点M 在OA 上，且OM⃑⃑⃑⃑⃑⃑⃑=2MA ⃑⃑⃑⃑⃑⃑⃑，N 为BC 中点，则MN⃑⃑⃑⃑⃑⃑⃑⃑（ ）A ．12a ⃑−23b ⃑⃑+12c ⃑B ．−23a ⃑+12b ⃑⃑+12c ⃑ C ．12a ⃑+12b ⃑⃑−12c ⃑D ．−23a ⃑+23b ⃑⃑−12c ⃑ 答案：B分析：由向量的加法和减法运算法则计算即可．MN ⃑⃑⃑⃑⃑⃑⃑⃑=ON ⃑⃑⃑⃑⃑⃑⃑−OM ⃑⃑⃑⃑⃑⃑⃑=12(OB ⃑⃑⃑⃑⃑⃑+OC ⃑⃑⃑⃑⃑⃑)−23OA ⃑⃑⃑⃑⃑⃑=−23a ⃑+12b ⃑⃑+12c ⃑ 故选：B5、已知椭圆x 2a 2+y 2b 2=1(a >b >0)上存在点P ，使得|PF 1|=3|PF 2|，其中F 1，F 2分别为椭圆的左、右焦点，则该椭圆的离心率的取值范围是（ ）A ．(0,14]B ．(14,1)C ．(12,1)D ．[12,1)答案：D分析：先由椭圆的定义结合已知求得|PF 1|,|PF 2|，再由|PF 1|−|PF 2|≤|F 1F 2|求得a,c 的不等关系，即可求得离心率的取值范围.由椭圆的定义得|PF 1|+|PF 2|=2a ，又∵|PF 1|=3|PF 2|，∴|PF 1|=32a ，|PF 2|=12a ，而|PF 1|−|PF 2|≤|F 1F 2|=2c ，当且仅当点P 在椭圆右顶点时等号成立，即32a −12a ≤2c ，即a ≤2c ，则e =c a ≥12，即12≤e <1.故选：D ．6、如图，下列各正方体中，O 为下底面的中心，M ，N 为顶点，P 为所在棱的中点，则满足MN ⊥OP 的是（ ）A ．B ．C ．D ．答案：A 分析：根据给定条件，建立空间直角坐标系，再对每一个选项逐一分析，利用空间位置关系的向量证明推理作答.在正方体中，对各选项建立相应的空间直角坐标系，令正方体棱长为2，点O (1,1,0)，对于A ，M (0,0,2),N (2,0,0),P (2,0,1)，MN ⃑⃑⃑⃑⃑⃑⃑ =(2,0,-2),OP ⃑⃑⃑⃑⃑ =(1,-1,1)，MN ⃑⃑⃑⃑⃑⃑⃑ ⊥OP ⃑⃑⃑⃑⃑ =0，MN ⊥OP ，A 是；对于B ，M (2,0,2),N (0,2,2),P (0,2,1)，MN ⃑⃑⃑⃑⃑⃑⃑ =(-2,2,0),OP ⃑⃑⃑⃑⃑ =(-1,1,1)，MN ⃑⃑⃑⃑⃑⃑⃑ ⊥OP ⃑⃑⃑⃑⃑ =4≠0，MN 与OP 不垂直，B 不是；对于C ，M (0,2,2),N (0,0,0),P (2,1,2)，MN →=(0,-2,-2),OP →=(1,0,2)，MN ⃑⃑⃑⃑⃑⃑⃑ ⊥OP ⃑⃑⃑⃑⃑ =-4≠0，MN 与OP 不垂直，C 不是；对于D ，M (2,2,2),N (0,2,0),P (0,0,1)，MN⃑⃑⃑⃑⃑⃑⃑ =(-2,0,-2),OP ⃑⃑⃑⃑⃑ =(1,0,1)，MN ⃑⃑⃑⃑⃑⃑⃑ ⊥OP ⃑⃑⃑⃑⃑ =-4≠0，MN 与OP 不垂直，D 不是.故选：A7、已知边长为2的等边三角形ABC ，D 是平面ABC 内一点，且满足DB:DC =2:1，则三角形ABD 面积的最小值是（ ）A ．43(√3−1)B ．43(√3+1)C ．4√33D ．√33 答案：A分析：建立直角坐标系，设D(x,y)，写出A,B,C 的坐标，利用DB:DC =2:1列式得关于x,y 的等式，可得点D 的轨迹为以(53,0)为圆心，以43为半径的圆，写出直线AB 的方程，计算|AB |和点D 距离直线AB 的最小距离d −r ，代入三角形面积公式计算.以BC 的中点O 为原点，建立如图所示的直角坐标系，则A(0,√3)，B (−1,0)，C (1,0)，设D (x,y )，因为DB:DC =2:1，所以(x +1)2+y 2=4(x −1)2+4y 2，得(x −53)2+y 2=169， 所以点D 的轨迹为以(53,0)为圆心，以43为半径的圆，当点D 距离直线AB 距离最大时，△ABD 面积最大，已知直线AB 的方程为：√3x −y +√3=0，|AB |=2，点D 距离直线AB 的最小距离为：d −r =|5√33+√3|2−43=4√33−43，所以△ABD面积的最小值为S△ABD=12×2×(4√33−43)=43(√3−1).故选：A8、已知抛物线C：y2=8x，点P为抛物线上任意一点，过点P向圆D：x2+y2−4x+3=0作切线，切点分别为A，B，则四边形PADB的面积的最小值为（）A．1B．2C．√3D．√5答案：C分析：由题意圆的圆心与抛物线的焦点重合，可得连接PD，则S四边形PADB=2S Rt△PAD=|PA|，而|PA|=√|PD|2−1，所以当|PD|最小时，四边形PADB的面积最小，再抛物线的定义转化为点P到抛物线的准线的距离的最小值，结合抛物线的性质可求得结果如图，连接PD，圆D：(x−2)2+y2=1，该圆的圆心与抛物线的焦点重合，半径为1，则S四边形PADB=2S Rt△PAD=|PA|．又|PA|=√|PD|2−1，所以当四边形PADB的面积最小时，|PD|最小．过点P向抛物线的准线x=−2作垂线，垂足为E，则|PD|=|PE|，当点P与坐标原点重合时，|PE|最小，此时|PE|=2．故(S四边形PADB )min=(√|PD|2−1)min=√3．故选：C9、如果复数z满足|z+1−i|=2，那么|z−2+i|的最大值是（）A．√13+2B．2+√3C．√13+√2D．√13+4答案：A分析：复数z满足|z+1−i|=2，表示以C(−1,1)为圆心，2为半径的圆．|z−2+i|表示圆上的点与点M(2,−1)的距离，求出|CM|即可得出．复数z满足|z+1−i|=2，表示以C(−1,1)为圆心，2为半径的圆．|z−2+i|表示圆上的点与点M(2,−1)的距离．∵|CM|=√32+22=√13．∴|z−2+i|的最大值是√13+2．故选：A．小提示：本题考查复数的几何意义、圆的方程，求解时注意方程|z+1−i|=2表示的圆的半径为2，而不是√2．10、动点P，Q分别在抛物线x2=4y和圆x2+y2−8y+13=0上，则|PQ|的最小值为（）A．2√3B．√3C．12√3D．32√3答案：B分析：设P(x0,14x02)，根据两点间距离公式，先求得P到圆心的最小距离，根据圆的几何性质，即可得答案.设P(x0,14x02)，圆化简为x2+(y−4)2=3，即圆心为（0,4），半径为√3，所以点P到圆心的距离d=√(x0−0)2+(14x02−4)2=√116(x02)2−x02+16，令t=x02，则t≥0，令f(t)=116t2−t+16，t≥0，为开口向上，对称轴为t=8的抛物线，所以f(t)的最小值为f(8)=12，所以d min=√12=2√3，所以|PQ|的最小值为d min−√3=2√3−√3=√3.故选：B填空题11、已知圆x2+y2+2x−4y−5=0与x2+y2+2x−1=0相交于A､B两点，则公共弦AB的长是___________. 答案：2分析：两圆方程相减可得公共弦所在直线方程，利用垂径定理即可得解.解：由题意AB所在的直线方程为：(x2+y2+2x−4y−5)−(x2+y2+2x−1)=0，即y=−1，因为圆x2+y2+2x−1=0的圆心O(−1,0)，半径为r=√2，所以，圆心O(−1,0)到直线y=−1的距离为1，所以|AB|=2√2−12=2.所以答案是：212、与双曲线x29−y216=1有共同渐近线，且经过点A(−3,2√3)的双曲线的一个焦点到一条渐近线的距离为___________.答案：2分析：由题意首先求得双曲线方程，据此可确定焦点坐标，然后利用点到直线距离公式可得双曲线的一个焦点到一条渐近线的距离.解：根据题意，设双曲线方程为x 29−y216=λ，将点(−3,2√3)代入双曲线方程，解得λ=14.所以，经过点A(−3,2√3)的双曲线方程为：4x 29−y24=1，故4x 29−y24=1的一个焦点坐标为(52,0),一条渐近线方程为y=43x，即4x−3y=0，所以，焦点到一条渐近线的距离是√9+16=2，所以答案是：213、设点M在直线2x+y−1=0上，点(3,0)和(0,1)均在⊙M上，则⊙M的方程为______________．答案：(x−1)2+(y+1)2=5分析：设出点M的坐标，利用(3,0)和(0,1)均在⊙M上，求得圆心及半径，即可得圆的方程.[方法一]：三点共圆∵点M在直线2x+y−1=0上，∴设点M为(a,1−2a)，又因为点(3,0)和(0,1)均在⊙M上，∴点M到两点的距离相等且为半径R，∴√(a−3)2+(1−2a)2=√a2+(−2a)2=R，a2−6a+9+4a2−4a+1=5a2，解得a=1，∴M(1,−1)，R=√5，⊙M的方程为(x−1)2+(y+1)2=5.所以答案是：(x−1)2+(y+1)2=5[方法二]：圆的几何性质由题可知，M是以（3，0）和（0，1）为端点的线段垂直平分线y=3x-4与直线2x+y−1=0的交点(1,-1).R=√5, ⊙M的方程为(x−1)2+(y+1)2=5.所以答案是：(x−1)2+(y+1)2=514、已知椭圆C:x24+y23=1的左､右焦点分别为F1，F2，M为椭圆C上任意一点，N为圆E:(x−3)2+(y−2)2=1上任意一点，则|MN|−|MF1|的最小值为___________.答案：2√2−5分析：首先根据椭圆的定义将|MN|−|MF1|的最小值转化为|MN|+|MF2|−4，再根据|MN|≥|ME|−1（当且仅当M、N、E共线时取等号），最后根据|ME|+|MF2|≥|EF2|求得|MN|−|MF1|的最小值.如图，由M为椭圆C上任意一点，则|MF1|+|MF2|=4又N为圆E:(x−3)2+(y−2)2=1上任意一点，则|MN|≥|ME|−1（当且仅当M、N、E共线时取等号），∴|MN|−|MF1|=|MN|−(4−|MF2|)=|MN|+|MF2|−4≥|ME|+|MF2|−5≥|EF2|−5，当且仅当M、N、E、F2共线时等号成立.∵F2(1,0)，E(3,2)，则|EF2|=√(3−1)2+(2−0)2=2√2，∴|MN|−|MF1|的最小值为2√2−5．所以答案是：2√2−5．小提示：思路点睛；本题主要考查与椭圆与圆上动点相关的最值问题，主要根据椭圆的定义将目标等价转化为能够通过数形结合解题的类型，考查学生的转化与化归思想，属于较难题.15、如图，已知点F为抛物线C:y2=4x的焦点过点F且斜率存在的直线交抛物线C于A，B两点，点D为准线l 与x轴的交点，则△DAB的面积S的取值范围为______．答案：(4,+∞)分析：设A, B 坐标和直线AB 的方程，让直线AB 方程与抛物线进行联立可得x 1+x 2=2+4k 2，x 1x 2=1，接着利用弦长公式求出|AB |，再求出点D 到直线AB 的距离，最后利用三角形的面积公式即可求出答案由抛物线C:y 2=4x 可得焦点F (1,0)，准线方程为x =−1，D (−1,0)，设A (x 1,y 1)，B (x 2,y 2)，直线AB 的方程为y =k (x −1)(k ≠0)，由{y =k (x −1)y 2=4x，可得k 2x 2−(2k 2+4)x +k 2=0，则x 1+x 2=2+4k 2，x 1x 2=1， 所以|AB |=√1+k 2⋅√(x 1+x 2)2−4x 1x 2=√1+k 2⋅√(2+4k 2)2−4=4(1+k 2)k 2， 直线AB 的一般方程为kx −y −k =0，点D (−1,0)到直线AB 的距离d =√k 2+1，所以S =12d ⋅|AB |=√1+k 2⋅4(1+k 2)k 2=4√1k 2+1>4， 所以△DAB 的面积S 的取值范围为(4,+∞)，所以答案是：(4,+∞)解答题16、已知△ABC 的三个顶点分别为A(−2，0)，B(2，0)，C(0，2)．（1）若过P(1，2)的直线y =ax +b 将△ABC 分割为面积相等的两部分，求b 的值；（2）一束光线从E(1，0)点出发射到BC 上的D 点，经BC 反射后，再经AC 反射到x 轴上的F 点，最后再经x 轴反射，反射光线所在直线为l ，证明直线l 经过一定点，并求出此定点的坐标．答案：（1）b =2−23√3；（2）证明见解析，(−1，−4)． 分析：（1）结合图形分析可得直线y =ax +b 的斜率大于直线PA 的斜率，由此可得直线y =ax +b 只能与BC 、AB 相交，设其与BC 的交点为Q 点，与x 轴的交点为R ，根据题设条件得到比例关系，列方程求b ；（2）设F(m ，0)，结合光线反射的性质求出直线ED 的斜率，由此可得直线l 的方程，进而可得定点坐标.（1）直线BC 的方程为：x +y―2=0，直线y =ax +b 只能与BC 、AB 相交，其与BC 的交点为Q 点，由{y =ax +b x +y =2得y Q =b+2a 1+a ，y Q >0， 直线y =ax +b 与x 轴交点为R (−b a ，0)，−2<b a <2，由|BR ||BQ ||BA ||CB |=12，即√2|2+b a ||b+2a 1+a |4×2√2=12， 化简得：(b +2a)2=4a (a +1)，又b +a =2， ∴3b 2−12b +8=0，解得：b =2±23√3， 而a =2−b >0，∴b =2−23√3．（2）设F(m ，0)，直线AC 的方程为：x −y +2=0，直线BC 的方程为：x +y −2=0，设F(m ，0)关于直线AC 的对称点为F 1(x 1，y 1)，则{m+x 12−y 12+2=0y 1x 1−m =−1 ，解得F 1(−2，m +2)，同理可得F 1关于直线BC 的对称点为F 2(−m ，4)，则F 2在直线ED 上，所以直线ED 的斜率为4−m−1，∴l 的斜率为4m+1，l 方程为y =4m+1(x −m )，即m (y +4)=4x −y ，∴l 过定点(−1，−4)．17、如图，在直三棱柱ABC −A 1B 1C 1中，AC ⊥BC ，AC =BC =BB 1，D 为AB 的中点．试用向量的方法证明：(1)BC 1⊥AB 1；(2)BC 1//平面A 1CD ．答案：(1)证明见解析(2)证明见解析分析：（1）建立空间直角坐标系，利用向量的方法证得结论成立.（2）利用向量的方法证得结论成立.（1）建立如图所示空间直角坐标系，设AC =BC =BB 1=2，则B (0,2,2),C 1(0,0,0),A (2,0,2),B 1(0,2,0)，BC 1⃑⃑⃑⃑⃑⃑⃑⃑=(0,−2,−2),AB 1⃑⃑⃑⃑⃑⃑⃑⃑=(−2,2,−2),BC 1⃑⃑⃑⃑⃑⃑⃑⃑⋅AB 1⃑⃑⃑⃑⃑⃑⃑⃑=0，所以BC 1⊥AB 1.（2）BC 1⃑⃑⃑⃑⃑⃑⃑⃑=(0,−2,−2)，D (1,1,2),A 1(2,0,0),C (0,0,2),DA 1⃑⃑⃑⃑⃑⃑⃑⃑⃑=(1,−1,−2),A 1C ⃑⃑⃑⃑⃑⃑⃑⃑=(−2,0,2)，设平面A 1CD 的法向量为n ⃑⃑=(x,y,z )，则{n ⃑⃑⋅DA 1⃑⃑⃑⃑⃑⃑⃑⃑⃑=x −y −2z =0n ⃑⃑⋅A 1C ⃑⃑⃑⃑⃑⃑⃑⃑=−2x +2z =0，故可令n ⃑⃑=(1,−1,1)， BC 1⃑⃑⃑⃑⃑⃑⃑⃑⋅n⃑⃑=0，所以BC 1//平面A 1CD .18、已知抛物线T ：y 2=2px （p ∈N +）和椭圆C ：x 25+y 2=1，过抛物线T 的焦点F 的直线l 交抛物线于A ，B 两点，线段AB 的中垂线交椭圆C 于M ，N 两点.(1)若F 恰是椭圆C 的焦点，求p 的值；(2)若MN 恰好被AB 平分，求△OAB 面积的最大值答案：(1)4(2)3√22．分析：（1）求出椭圆焦点，得抛物线焦点，从而得p 的值；（2）设直线l 方程为x =my +p 2，代入抛物线方程，结合韦达定理得中点坐标，根据椭圆的弦中点性质得出一个参数值，由中点在椭圆内部得出另一个参数的范围，然后求出三角形面积，得出最大值．（1）在椭圆中，c =√a 2−b 2=2， 所以p 2=2，p =4； （2）设直线l 方程为x =my +p 2，代入抛物线方程得y 2−2mpy −p 2=0，设A(x 1,y 1),B(x 2,y 2)，AB 中点为G(x 0,y 0)，则y 1+y 2=2mp ，y 1y 2=−p 2，y 0=y 1+y 22=mp ，x 0=m 2p +p 2，设M(x 3,y 3),N(x 4,y 4)，则{x 325+y 32=1x 425+y 42=1 ，两式相减得(x 3+x 4)(x 3−x 4)5+(y 3+y 4)(y 3−y 4)=0， 所以2x 0(x 3−x 4)5+2y 0(y 3−y 4)=0，k MN =y 3−y 4x 3−x 4=−x 05y 0，k MN =−1m ， 所以−15×m 2p+p 2mp =−1m ，解得m 2=18，点G 在椭圆内部，所以(m 2p+p 2)25+(mp)2<1，得p 2<6413， 因为p ∈N +，所以p =1或p =2，S △OAB =12×p 2|y 1−y 2|=p 4√(y 1+y 2)2−4y 1y 2=p 4√4m 2p 2+4p 2=3√28p 2， p =1时，S △OAB =3√28，p =2时，S △OAB =3√22， 所以△OAB 面积的最大值为3√22． 小提示：本题考查求抛物线的方程，考查直线民椭圆、抛物线相交问题，考查圆锥曲线中的面积问题．解题方法采用设而不求的思想方法，即设交点坐标，设直线方程，代入曲线方程后应用韦达定理，求得弦中点坐标，弦长等，把这个结论代入其他条件可求得参数关系，参数值，参数范围等．即设参数，利用韦达定理把目标用参数表示，进而求最值，证明一些结论．本题考查学生的逻辑推理能力，运算求解能力，对学生的要求较高，属于难题．19、已知直线l 1与直线l 2:3x +4y −5=0平行，直线l 1与两坐标轴所构成的三角形的面积为12，求直线l 1的方程. 答案：3x +4y ±12√2=0分析：设直线的方程为3x +4y +c =0，求出截距后可求面积，从而可求直线的方程.设直线l 1的方程为3x +4y +c =0.令y =0，得x =−c 3；令x =0，得y =−c 4.由题设得12|−c 3|⋅|−c 4|=12.解得c =±12√2，因此直线l 1的方程为3x +4y ±12√2=0.。

2024年湖北省初中学业水平考试语文试题(本试卷满分120分，考试用时150分钟)注意事项:1.答卷前，考生务必将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上指定位置。

2、选择题的作答:每小题选出答贵后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

写在试卷、草稿纸和答题卡上的非答题区域均无效。

3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内，写在试卷、草稿纸和答题卡上的非答题区域均无效。

4.考试结束后，请将试卷和答题卡一并交回。

一、积累与运用(20分)开展活动可以让语文学习更有意思。

小雨和小要设计了一些语文小活动，请你来参加。

1.(2分)右图是小雨展示的“楚”字的早期写法(由“林”和“足”构成)。

诸你据此猜想楚国先民的生活画面，用一句话说说:2.(2分)下面是小雯整理的关于“楚”字的资料卡片，请你在(1)(2)处分别补充一个含“楚”字的词语。

“楚”的本义“楚”的引申义含“楚”字的词语“楚”是一种丛生落叶清晰明了清楚灌木。

(比一般灌木长有痛苦、心酸的感觉（1）得高,远看一目了然,清晰整齐；制成荆条韧性好。

)“楚楚”连用表示鲜明整洁、娇柔秀美（2）3.(2分)小雨和小雯为学校作了一副对联。

小雨写的是“情系中华竞芳华”小雯写的是“根植荆楚育翘楚”。

请你确定上下联，参照横批把这副对联工整地抄写到相应位置(见右图)。

4.(8分)小雨在“分门别类辑名句”活动中编写了下面这段话，请你依据学过的古诗文将这段话补充完整。

诸葛亮隐居隆中,“苟全性命于乱世， ①”；杜牧赤壁怀古,“东风不与周郎便, ②”。

周敦颐借莲言志:“予独爱莲之出淤泥而不染， ③ 。

”岑参以花喻雪:“忽如一夜春风来， ④。

”刘禹锡吟诗酬和：“沉舟侧畔千机过， ⑤。

”苏东坡望月抒怀:“人有悲欢离合, ⑥，此事古难全。

”过三峡听渔者歌曰:“巴东三峡巫峡长， ⑦ 。

”登黄鹤楼随诗人吟诵:“ ⑧，芳草萋萋鹦鹉洲。

四川省部分中学2023高中语文必修上第一单元解题技巧总结选择题1、下列诗句与作品、作者对应正确的一项是A．你好呵，欢乐的精灵！——《红烛》——闻一多B．力的绘画，力的舞蹈，力的音乐，力的诗歌，力的律吕哟——《致云雀》——郭沫若C．我的指关节铆钉一样楔入巨石的罅隙——《立在地球边上放号》——昌耀D．鹰击长空，鱼翔浅底，万类霜天竞自由——《沁园春·长沙》——毛泽东答案：D本题考查识记文学常识的能力。

做此题时，要求考生在调动平时学习积累的时候要放开眼界，多去关注一些传统文化知识和中外文化常识，尤其是课本的注释的相关内容，重点记忆课本涉及到的和经典阅读中列出的作品。

平时注意积累，理出线索，形成体系。

A项，“你好呵，欢乐的精灵！”是雪莱《致云雀》中的句子；B项，《致云雀》应为《立在地球边上放号》；C项，“《立在地球边上放号》”应为“《峨日朵雪峰之侧》”。

故选D。

小提示：文学常识类题目考查内容较为广泛，需要考生长期注重文化积累。

文学常识的考核主要集中的中外中的作家、作品，文学现象、文学流派，文体知识等。

重点记忆课本涉及到的和经典阅读中列出的作品。

平时注意积累，理出线索，形成体系。

在做题时，也要关注某一个细节或者某一个用词上出现的瑕疵和陷阱，做到仔细甄别。

2、下列句子翻译，不正确的一项是（）A．指点江山，激扬文字，粪土当年万户侯。

译文：评论国家大事，写出激浊扬清的文章，把当时的军阀官僚看得同粪土一样。

B．熊咆龙吟殷岩泉，栗深林兮惊层巅。

译文：熊在咆哮，龙在长吟。

声音震荡着岩石和泉水，使深林战栗，使层巅震惊。

C．师者，所以传道受业解惑也。

译文：老师，是依靠他来传授道、教授学业、解除疑惑的人。

D．君子博学而日参省乎己，则知明而行无过矣。

译文：君子学识渊博，而且每天参加反省自己，就知道明白而且行为没有错误了。

答案：D本题考查学生对文言语句的翻译能力。

D项，选项翻译错误，正确翻译为：君子广泛地学习而且每天对自己检查、省察，就能见识明达，行动不犯错误了。