奥数算式谜

（三年级）暑期备课教员：第三讲算式谜（一）一、教学目标： 1. 会分析算式中所包含的数量关系，能找出隐蔽条件，选择有特征的部分作出局部判断。

2. 会利用列举和筛选结合的方法，逐步排除不合理的数字。

3. 试验时，能借助估值的方法，以缩小所求数字的取值范围，达到快速而准确的目的；4. 算式谜解出后，知道要验算一遍。

二、教学重点：找出隐蔽条件，利用列举和筛选相结合方法。

三、教学难点：列举和筛选方法。

四、教学准备：PPT五、教学过程：第一课时（50分钟）一、创设情景，激情导入（5分)师：今天给大家讲一个故事：小淘气一天，小淘气跑到爸爸的书房，想看看他的工程师爸爸天天都在忙什么，结果不小心把一瓶墨水碰洒了，这下可把小淘气吓坏了，仔细一看，墨水把一道写着算式的一些数字涂上了，怎么办呢？小淘气冥思苦想后，他推算出了所有被墨水涂上的数字。

爸爸回来后，不但没有批评他，还说他是个爱思考的好孩子。

师：小朋友们你们想知道是什么算式吗？生：想。

师：（出示算式）那就让我们一起来看一下吧！生：……师：大家知道这是什么吗？生：算式谜。

师：是的，今天这节课我们就一起来学习算式谜（板书——算式谜（一））师：那大家会不会算呢？生：……师：我们就一起去看看吧！二、探索发现授课（40分）（一）例题一：（13分）在□内填入合适的数字，使竖式成立。

师：同学们，我们先看一下这两个算式，说一说你想说什么？ 生：……师：第一个算式你是怎么想的？生：我们可以先找出它的突破口。

师：谁来说一下第一小题的突破口在哪？ 生：在个位。

师：怎么算呢？生1：已知一个加数的个位是6，还知道和的个位是5，可以求出第一个加数个 位上的方框中填9。

生2：因为（9）+6=15，向十位进1，个位上是5，所以个位上方框填9。

师：很好，我们再来看哪一位？ 生：再来看十位。

师：是的，十位上又怎么填呢？生：十位上有一个加数是1及个位进的1，而和是一个四位数，所以我们要考虑 到十位上要有进位。

学生课程讲义课程名称三年级奥数上课时间任课老师沈老师第 5 讲，本讲课题：算式之谜 内容概要小朋友都喜欢猜谜语,你们知道数学中也有一种有趣的谜吗?一个算式中缺少几个数字,那就成了一道算式谜。

算式谜又被称为“虫食算”,意思是说算式中的一些数字像是被虫子咬去了。

解算式谜,就是要将算式中缺少的数字补全,使它成为一个完整的算式。

解算式谜的思考方法是推理加上尝试。

先要仔细观察算式的特征,由推理能确定的数字先填上；由推理不能确定的数字要分几种情况逐一尝试。

分析时要认真分析已知数字与所缺数字之间的关系,找准解题的突破口。

【例1】在下面算式的□内，填上适当的数字，使算式成立。

举一反三在□里填上适当的数，使算式成立。

【例2】□里填哪些数字，可使这道除法算式成为一道完整的算式？举一反三【例3】□里填哪些数字，可使这道除法算式成为一道完整的算式？举一反三练习2：在□里填上适当的数，使算式成立。

【例4】在下面竖式的□里，各填入一个合适的数字，使算式成立。

：举一反三在□里填上适当的数，使算式成立。

6575（2）（1）048（2）42818（1）【例5】在下面竖式的□里，各填入一个合适的数字，使算式成立。

举一反三【例题5】在下面□中填入适当的数，使算式成立。

举一反三在下面□中填入适当的数，使算式成立。

练习：4427（2）296250（1）5354152（2）（1）2110936。

第8讲 算式谜一、知识要点一个完整的算式，缺少几个数字，那就成了一道算式谜.解算式谜，就是要将算式中缺少的数字补齐，使它成为一道完整的算式.解算式谜的思考方法是推理加上尝试，首先要仔细观察算式特征，由推理能确定的数先填上；不能确定的，要分几种情况，逐一尝试.分析时要认真分析已知数字与所缺数字的关系，抓准解题的突破口. 二、精讲精练【例题1】在下面算式的□内，填上适当的数字，使算式成立.练习1：在□里填上适当的数，使算式成立.【例题2】□里填哪些数字，可使这道除法算式成为一道完整的算式？ 练习2：在□里填上适当的数，使算式成立.6575（2）（1）048【例题3】在下面竖式的□里，各填入一个合适的数字，使算式成立. 答案：练习3： □里可以填哪些数字？【例题4】在下面竖式的□里，各填入一个合适的数字，使算式成立.答案：练习4：在下面竖式的□里，各填入一个合适的数字，使算式成立.【例题5】在下面□中填入适当的数，使算式成立.答案：71707174982882717391211214414827170（2）42818（1）44277443006864278232332323724282003447（2）52962504（1）488221204481646861424880221练习5：在下面□中填入适当的数，使算式成立.5354152（2）（1）211936。

第32讲算式谜一、专题简析：算式谜一般是指一些含有未知数或缺少运算符号的算式。

解决这类问题，可以根据四则运算的规定，四则运算算式中的数量关系以及数的组成，逐步确定算式中的未知数和运算符号。

解答算式谜的关键是找准突破口，推理时应注意：1、认真分析算式中所包含的数量关系，找出尽可能多的隐蔽条件，选择有特征的部分作出局部判断；2、采用列举和筛选相结合的方法，逐步排除不合题意的数字；3、算式谜解出后，务必要验算一遍。

二、精讲精练例题1 有一个六位数，它的个位数字是6，如果将6移至第一位前面，所得的新六位数是原数的4倍。

求原六位数。

练习一1、已知六位数1ABCDE，这个六位数的3倍正好是ABCDE1，求这个六位数。

2、下面式子中每个汉字代表一个数字，不同的汉字代表不同的数字，请说出各个汉字分别代表什么数字。

2华罗庚金杯×3=华罗庚金杯2例题2 下面竖式中每个小方格都代表一个数字，请把这个算式写完整。

2 8 5×□□1 □2 □□□□□ 9 □□练习二1、把下面的算式写完整。

□□□× 8 9□□□□□□□□□□□2、在算式的（）里填上合适的数字。

（） 2 （）（）×（） 6（）（） 0 4（）（） 7 （）（）（）（）（）（）例题3下图的五个方格中已经填入84和72两个两位数，请你在其余的三格中也分别填入一个两位数，使得横行的三个数与竖行的三个数之和相等，并且这五个两位数正好由0～9十个数字组成。

练习三1、把0～9这十个数字填到圆圈内，每个数字只能用一次，使三个算式成立。

○＋○=○○－○=○○×○=○○2、将1～9九个数字填入下列九个○中，使等式成立。

○○○×○○=○○×○○=5568例题4 把0、1、2、3、4、5、6、7、8、9这十个数字填入下面的小方格中，使三个等式都成立。

□＋□=□□－□=□□×□=□□练习四1、将1、2、3、4、5、6、7、8、9九个不同的数字分别填在○中，使下面的三个算式成立。

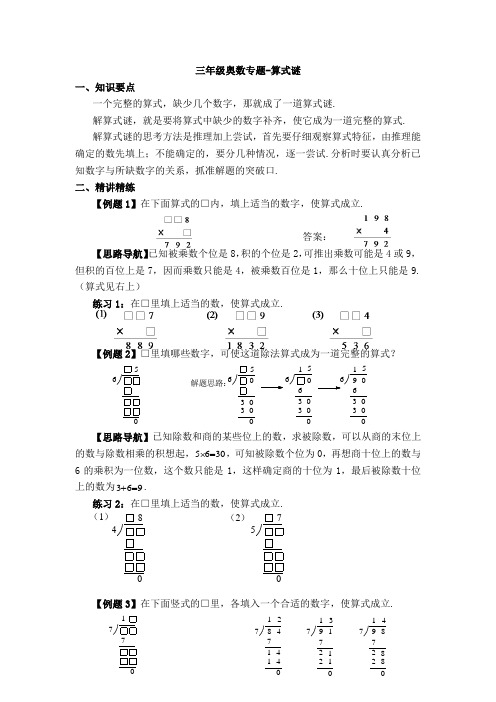
三年级奥数专题-算式谜一、知识要点一个完整的算式，缺少几个数字，那就成了一道算式谜.解算式谜，就是要将算式中缺少的数字补齐，使它成为一道完整的算式. 解算式谜的思考方法是推理加上尝试，首先要仔细观察算式特征，由推理能确定的数先填上；不能确定的，要分几种情况，逐一尝试.分析时要认真分析已知数字与所缺数字的关系，抓准解题的突破口. 二、精讲精练【例题1】在下面算式的□内，填上适当的数字，使算式成立.答案：【思路导航】已知被乘数个位是8，积的个位是2，可推出乘数可能是4或9，但积的百位上是7，因而乘数只能是4，被乘数百位是1，那么十位上只能是9.（算式见右上）练习1：在□里填上适当的数，使算式成立.【例题2】□里填哪些数字，可使这道除法算式成为一道完整的算式？【思路导航】已知除数和商的某些位上的数，求被除数，可以从商的末位上的数与除数相乘的积想起，5630⨯=，可知被除数个位为0，再想商十位上的数与6的乘积为一位数，这个数只能是1，这样确定商的十位为1，最后被除数十位上的数为369+=.练习2：在□里填上适当的数，使算式成立. 【例题3】在下面竖式的□里，各填入一个合适的数字，使算式成立.0659300305661160650300330030解题思路：560750（2）（1）04871707174982882717391211214414827170答案：【思路导航】要求□里填哪些数，我们可以先想被除数的十位上的数是多少.容易知道，被除数的十位数字比7大，只可能是8或9.如果十位数字是8，那么商的个位只能是2；如果十位数字是9，那么商的个位是3或4.所以，这道题有三种填法（见上页）.练习3： □里可以填哪些数字？ 【例题4】在下面竖式的□里，各填入一个合适的数字，使算式成立.答案：【思路导航】通过观察，我们发现，由于余数是7，则除数必须比7大，且被除数个位上应填7；由于商是4时是除尽的，所以被除数十位上应为2，同时3412 , 84=32⨯=⨯，因而除数可能是3或8，可是除数必须比7大，因而除数只能是8，因而被除数百位上是3，而商的百位上为0，商的千位是8或3，所以一共有两种填法（见上）.练习4：在下面竖式的□里，各填入一个合适的数字，使算式成立. 【例题5】在下面□中填入适当的数，使算式成立.答案：【思路导航】通过观察，我们发现，商的个位8与除数的乘积是48，由此可求出除数为6.再根据商的千位与6的乘积是二十几，于是可求出商的千位是4，因而被除数的万位是2，千位是4，然后可求出商的百位是0，十位是2，被除数（2）42818（1）44277443006864278232332323724282003447（2）52962504（1）488221204481646861424880221的百位是1，十位是6，个位是8.（填法见上）练习5：在下面□中填入适当的数，使算式成立.5354152（2）（1）211936。

五年级奥数专题-算式谜【专题导引】算式谜一般是指一些含有未知数字或缺少运算符号的算式。

解决这类问题,可以根据四则运算的规定、四则运算算式中的数量关系以及数的组成,逐步确定算式中的未知数字和运算符号。

解答算式谜的关键是找准突破口,推理时应注意：1、认真分析算式中所包含的数量关系,找出尽可能多的隐蔽条件,选择有特征的部分做出局部判断。

2、采用列举和筛选结合的方法,逐步排除不合题意的数字。

3、算式谜解出后,务必要验算一遍。

【典型例题】【例1】有一个六位数,它的个位数字是6,如果将6移至第一位前面,所得的新六位数是原数的4倍。

求原六位数。

【试一试】1、已知六位数ABCDE 1,这个六位数的3倍正好是1ABCDE 。

求这个六位数。

2、下面竖式中每个汉字表示一个数字,不同的汉字表示不同的数字,请说出各个汉字分别表示什么数字？【例2】下面竖式中每个小方格都代表一个数字,请把这个算式写完整。

２华罗庚金杯 × ３ 华罗庚金杯２ ２８５× □□１□２□□□□□９□□８４ ７２□□□ × ８９ □□□□ □□□ □□□□ □２□□ × □６ □□０４ □□７０ □□□□□ 【试一试】1、把下面的算式写完整。

2、在算式的“□”里填上合适的数字。

【例3】右图的五个方格中已经填写入84和72两个两位数,请你在其余的三格中也分别填入一个两位数,使得横行的三个数与竖行的三个数之和相等,并且这五个两位数正好由0～9十个数字组成。

【试一试】1、把0～9这十个数字填到圆圈内,每个数字只能用一次,使三个算式成立。

○+○=○ ○-○=○ ○×○=○○2、将1～9九个数字填入下列九个○中,使等式成立。

○○○×○○=○○×○○=5568【例4】把0、1、2、3、4、5、6、7、8、9这十个数字填入下面的小方格中,使三个等式都成立。

□＋□=□□－□=□□×□=□□【试一试】1、将1、2、3、4、5、6、7、8、9九个不同的数字分别填在○中,使下面的三个算式成立。

第11讲文字算式谜一、精讲精练【例题1】下式中，每个字各代表一个不同的数字，其中“心”代表9，请问其他汉字分别代表哪个数字？练习1：1．下面（左下）每个字代表不同的数字，这些汉字分别代表几？2．如果A、B满足下面算式，它们各代表几？（上中）3．上右图各个汉字分别代表几？【例题2】下面不同的汉字代表不同的数字，相同的汉字代表相同的数字。

它们各表示几？练习2：下面各个竖式中的汉字分别代表几？×【例题3】在下面的竖式中，a 、b 、c 、d 各代表什么数字?练习3：1．下面（左下）竖式中的字母各代表几？2．上面（右上）竖式中的字母各代表几？ A ＋B ＋C=（ ）【例题4】下面算式里，相同的汉字代表同一个数字，不同的汉字代表不同的数字。

如果以下3个等式成立：小小×朋朋=友小小友爱爱×科科=爱学学爱朋朋×朋朋=小小学学练习4：下面算式里，相同的汉字代表同一个数字，不同的汉字代表不同的数字。

则每个汉字分别代表什么数。

×× 那么，小=（ ） 朋=（ ） 友=（ ） 爱=（ ） 科=（ ） 学=（ ）【例题5】下面算式中四个字分别代表四个数，你能求出来吗？新=（）年=（）快=（）乐=（）练习5：1．下面（左下）算式中相同的汉字代表相同的数字，不同的汉字代表不同的数字，请问这些汉字各代表几？2．上面（上中）各字母分别代表几？3．上面（上右）竖式中每个字母代表不同的数字，想想下面的算式怎样写？二、课后作业：1.下面各题中○、☆各代表一个数，求出它们各代表什么数。

（1）☆+☆－8＝14（2）18×○－16×○＝482.在下面竖式的方框里填上合适的数字使竖式成立。

3.求下列各题中△各代表什么数。

（1）△+△＝18－6（2）2×△+4×△＝24×44.在□里填上合适的数，使竖式成立。

5.在□里填上合适的数，使竖式成立。

三年级奥数算式谜教案【篇一：三年级奥数专题之算式谜】算式谜算式谜是一种有趣的数学问题，它的特点是在算术运算的式子中，使一些数字或运算符号“残缺”，要我们根据运算法则，进行判断推理，从而把“残缺”的算式补充完整。

研究和解决算式谜问题，有利于培养我们观察、分析、归纳、推理等思维能力。

从这个意义上讲，算式谜问题是一种很好的锻炼思维的“体操”。

例1、在下面算式的括号里填上合适的数。

（1）（）6（）（）（2）（）0（）（）+ 2（）15 - 3（） 1 68 0 914 857巩固：在“庆元旦”晚会上，主持人小丽出了这样两道题目：1916711066请大家想一想，被纸片盖住的是什么数字?例2．a、b、c、d分别代表4个不同的数字，相同的字母代表相同的数字，求使得下面算式成立a、b、c、d各自代表的数字。

a b c da c d+c d1 9 8 9巩固：下面的符号各表示几？19189356197例3．a、b、c、d它们各是什么数字时同上面的算式成立？ 83分别代表不同的数字，a b c d-c d c a b c1、、23、、45、、、678、9这十个数字组成下面的加法算式，每个数字只许用一巩固：用0、次，现已写出3个数字，请把这个算式补齐．42例4．下面的算式中的“数”、“学”、“俱”、“乐”、“部”这五个汉字各应代表什么数字？8巩固：下面算式中不同的字母所找表的数字均不同，当这些字母代表什么数时，算式成立？例5、下面的算式里四个小纸片各盖住一个数字，问被盖住的四个数字的和是多少?149巩固：下面的算式里，每个方框代表一个数字，问：这6个方框中数字的总和是多少?1991课后作业1．下面算式中不同的图形代表不同的数，不同的字母代表不同的数，请将算式中的图形或字母还原成数字。

(1) 1 ○ 2 □(2) a b c d -□ 1 △ + a b e d3 ○ ○ e d c a d2、在下列竖式的空格内，各填入一个合适的数字，使竖式成立.397211493、下面的符号代表几？7458213184134．下面算式中汉字或字母分别代表不同的数字，请将汉字或字母还原成数字。

第5讲算式谜（一）算式谜是一种有趣的数学问题，它的特点是在算术运算的式子中，使一些数字或运算符号“残缺”，要我们根据运算法则，进行判断推理，从而把“残缺”的算式补充完整。

研究和解决算式谜问题，有利于培养我们观察、分析、归纳、推理等思维能力。

从这个意义上讲，算式谜问题是一种很好的锻炼思维的“体操”。

例1.在下面算式的括号里填上合适的数。

（1）（）6（）（）（2）（）0（）（）+ 2（）1 5 - 3（） 1 68 0 9 1 4 8 5 7例2．A、B、C、D分别代表4个不同的数字，相同的字母代表相同的数字，求使得下面算式成立A、B、C、D各自代表的数字。

A B C DA C D+ C D1 9 8 9例3．A、B、C、D分别代表不同的数字，它们各是什么数字时同上面的算式成立？A B C D- C D CA B C例4．下面的算式中的“数”、“学”、“俱”、“乐”、“部”这五个汉字各应代表什么数字？1 数学俱乐部× 3数学俱乐部 1例5．下面算式中不同的字母所找表的数字均不同，当这些字母代表什么数时，算式成立？A B C× D CB E AF AG HF IG A A例6．在括号里填数，使下面的竖式成立。

1（）（）（））1（）21（）7 （）（）（）例7.下面的算式中，相同的汉字代表相同的数字，不同的汉字代表不同的数字，求这个算式。

新新×春春=新年年新练习与思考1．在□里填上适当的数，使等式成立。

(1)□ 6 4 (2)□ □ 37 □ 3 - □ □+ 4 8 □ 8□ 0 4 22．下面算式中不同的图形代表不同的数，不同的字母代表不同的数，请将算式中的图形或字母还原成数字。

(1) 1 ○ 2 □ (2) A B C D- □ 1 △ + A B E D3 ○ ○ E D C A D3．在（ ）里填上适当的数，使算式成立。

4．下面算式中汉字或字母分别代表不同的数字，请将汉字或字母还原成数字。