小学奥数- 算式谜(一)

第5周算式谜（一）一、知识要点“算式谜”一般是指那些含有未知数字或缺少运算符号的算式。

解决这类问题，可以根据已学过的知识，运用正确的分析推理方法，确定算式中的未知数字和运用符号。

由于这类题目的解答过程类似全平时进行的猜谜语游戏，所以，我们把这类题目称为“算式谜题”。

解答算式谜问题时，要先仔细审题，分析数据之间的关系，找到突破口，逐步试验，分析求解，通常要运用倒推法、凑整法、估值法等。

二、精讲精练【例题1】在下面算式的括号里填上合适的数。

【思路导航】根据题目特点，先看个位：7＋5＝12，在和的个位（）中填2，并向十位进一；再看十位，（）＋4＋1的和个位是1，因此，第一个加数的（）中只能填6，并向百位进1；最后来看百位、千位，6＋（）＋1的和的个位是2，第二个加数的（）中只能填5，并向千位进1；因此，和的千位（）中应填8。

练习1：（1）在括号里填上合适的数。

（2）在方框里填上合适的数。

（3）下面的竖式里，有4个数字被遮住了，求竖式中被盖住的4个数字的和。

【例题2】下面各式中“巨”、“龙”、“腾”、“飞”分别代表不同的数字，相同的汉字代表相同的数字。

当它们各代表什么数字时，下列的算式成立。

【思路导航】先看个位，3个“飞”相加的和的个位数字是1，可推知“飞”代表7；再看十位，3个“腾”相加，再加上个位进来的2，所得的和的个位是0，可推知“腾”代表6；再看百位，两个“龙”相加，加上十位进上来的2，所得和的个位是0，“龙”可能是4或9，考虑到千位上的“巨”不可能为0，所以“龙”只能代表4，“巨”只能代表1。

练习2：【例题3】下面各式中的“兵”、“炮”、“马”、“卒”各代表0—9这十个数字中的某一个，相同的汉字代表相同的数字。

这些汉字各代表哪些数字？【思路导航】这道题应以“卒”入手来分析。

“卒”和“卒”相加和的个位数字仍然是“卒”，这个数字只能是0。

确定“卒”是0后，所有是“卒”的地方，都是0。

注意到百位上是“兵”＋“兵”＝“卒”，容易知道“兵”是5，“车”是1；再由十位上的情况可推知“马”是4，进而推得“炮”是2。

1.右边竖式中的每个汉字代表不同的数字，这些汉字各代表哪些数字？少（）年（）早（）立（）志（）向（）有（）何（）惧（）2．右式中不同的汉字代表1～9中不同的数字，当算式成立时，“中国”这两个汉字所代表的两位数最大是________。

3．右面的算式里，每个方框代表一个数字。

问：这6个方框中的数字的总和是________。

4．下边是一道题的乘法算式，请问：A、B、C、D、E分别代表什么数字？5．右边残缺算式中已知3个4，那么补全后它的乘积是___________。

6.解算式谜： (下列竖式中的每个汉字、字母各代表不同的数字 )巧（）解（）趣（）题（）妙（）趣（）横（）生（）7．下面算式均由1，2，……9九个数字组成，请填空使算式成立。

1．在下面算式的□内，填上适当的数字，使算式成立．2．在下面算式的□内，填上适当的数字，使算式成立．3．在下面算式的□内，填上适当的数字，使算式成立．4．在下面算式的□内，填上适当的数字，使算式成立．5．右面竖式“春夏秋冬四季”分别代表什么数字？春=（）夏=（）秋=（）冬=（）四=（）季=（）年=（）奥数基础－竖式数字谜（3）1．在下面算式的□内，填上适当的数字，使算式成立．2．右面的算式里，每个方框代表一个数字，问这六个方框中的数字的总和是____。

3．在下面算式的□内，填上适当的数字，使算式成立．3、（1）“争当小雏鹰”分别代表什么数字？（2）下式中“优”代表什么数字？争=（）当=（）小=（）雏=（）鹰=（）学=（）习=（）再=（）优=（）4．右面竖式中的每个不同汉字代表0～9中不同的数码，求出它们使得竖式成立的值。

巧=（）解=（）数=（）字=（）谜=（）。

5-1-1-1.算式謎（一）教學目標數字謎從形式上可以分為橫式數字謎與豎式數字謎，從運算法則上可以分為加減乘除四種形式的數字謎。

橫式與豎式亦可以互相轉換，本講中將主要介紹數字謎的一般解題技巧。

主要橫式數字謎問題，因此，會需要利用數論的簡單奇偶性等知識解決數字謎問題。

知識點撥一、基本概念填算符：指在一些數之間的適當地方填上適當的運算符號（包括括弧），從而使這些數和運算符號構成的算式成為一個等式。

算符：指+、-、×、÷、（）、[]、｛｝。

二、解決巧填算符的基本方法（1）湊數法：根據所給的數，湊出一個與結果比較接近的數，再對算式中剩下的數字作適當的增加或減少，從而使等式成立。

（2）逆推法：常是從算式的最後一個數字開始，逐步向前推想，從而得到等式。

三、奇數和偶數的簡單性質（一）定義：整數可以分為奇數和偶數兩類（1）我們把1，3，5，7，9和個位數字是1，3，5，7，9的數叫奇數.（2）把0，2，4，6，8和個位數是0，2，4，6，8的數叫偶數.（二）性質：①奇數≠偶數.②整數的加法有以下性質：奇數+奇數=偶數；奇數+偶數=奇數；偶數+偶數=偶數.③整數的減法有以下性質：奇數-奇數=偶數；奇數-偶數=奇數；偶數-奇數=奇數；偶數-偶數=偶數.④整數的乘法有以下性質：奇數×奇數=奇數；奇數×偶數=偶數；偶數×偶數=偶數.例題精講模組一、巧填算符（一）巧填加減運算符號【例1】在下面算式適當的地方添上加號，使算式成立。

88888888=1000【考點】巧填算符之湊數法【難度】3星【題型】填空【解析】要在八個8之間只添加號，使和為1000，可先考慮在加數中湊出一個較接近1000的數，它可以是888，而888＋88=976，此時，用去了五個8，剩下的三個8應湊成1000-976＝24，這只要三者相加就行了。

本題的答案是：888+88+8+8+8=1000【答案】888+88+8+8+8=1000【例2】在等號左邊9個數字之間填寫6個加號或減號組成等式：1 2 3 4 56 7 8 9＝101【考點】巧填算符之湊數法【難度】3星【題型】填空【關鍵字】迎春杯，中年級，初賽，第2題【解析】（不唯一）123456789101++++-+=或123456789101-+-+++=【答案】123456789101++++-+=或123456789101-+-+++=【例3】在下面的□中填入“+”、“一”，使算式成立：1110987654210=□□□□□□□□3□□【考點】巧填算符之湊數法【難度】3星【題型】填空【關鍵字】希望杯，4年級，初賽，5題【解析】11+10+9-8-7-6-5-4+3-2-1=0.(答案不唯一)【答案】11+10+9-8-7-6-5-4+3-2-1=0.(答案不唯一)【巩固】在下面的□中填入“+”、“一”，使算式成立：11109876321=□□□□□□5□4□□【考點】巧填算符之湊數法【難度】3星【題型】填空【關鍵字】希望杯，六年級，初賽，第2題，6分【解析】11+10+9……3+2=65，所以只要將其中和為32的幾項的加號改成減號即11-10-9-8+7+6-5+4+3+2=1【答案】11-10-9-8+7+6-5+4+3+2=1【例4】在下面算式中合適的地方，只添兩個加號和兩個減號使等式成立。

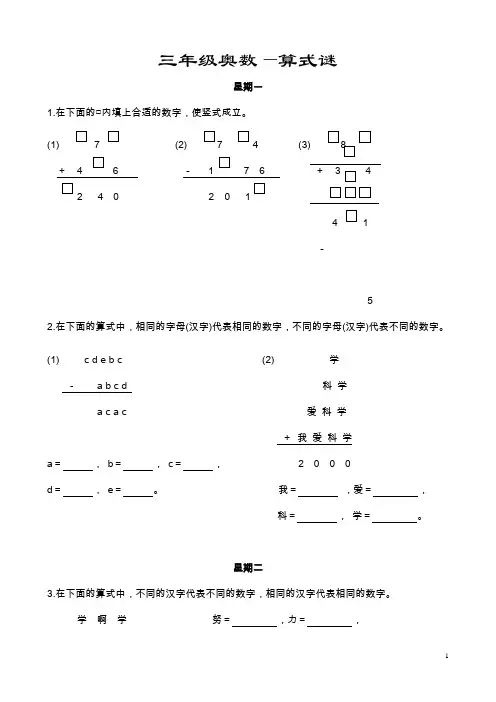
三年级奥数—算式谜星期一1.在下面的□内填上合适的数字，使竖式成立。

(1) 7 (2) 7 4 (3) 8＋ 4 6 － 1 7 6 ＋ 3 42 4 0 2 0 14 1－52.在下面的算式中，相同的字母(汉字)代表相同的数字，不同的字母(汉字)代表不同的数字。

(1) c d e b c (2) 学－ a b c d 科学a c a c 爱科学＋我爱科学a＝，b＝，c＝， 2 0 0 0d＝，e＝。

我＝，爱＝，科＝，学＝。

星期二3.在下面的算式中，不同的汉字代表不同的数字，相同的汉字代表相同的数字。

学啊学努＝，力＝，＋努力学学＝，啊＝。

努力学啊4.在下面的算式中，不同的汉字代表不同的数字，相同的汉字代表相同的数字。

参加比赛我＝，参＝，＋参加比赛加＝，比＝，我加比参赛赛＝。

5.在下面的算式中，不同的汉字代表不同的数字，相同的汉字代表相同的数字。

数字常＝，字数数＝，＋数字字＝。

常常数星期三6. 在下面的□内填上合适的数字，使竖式成立。

(1) 3 2 (2) 98 －9＋ 3 98 1 8 3－9 ＋5 07.(1)已知：□□＋□□＝169，则这4个□中的数字的总和是。

(2)已知：□□□□＋□□□□＝19991，则这8个□中的数字的总和是。

8.在下面的算式中，字母A、B、C、D、E、F、G代表1～9中的7个数字。

不同的字母代表不同的数字，相同的字母代表相同的数字。

求A＋B＋C＋D＋E＋F＋G＝？A B C D＋ E F G2 0 1 1星期四9.在下面的算式中，相同的字母(文字)代表相同的数字，不同的字母(文字)代表不同的数字。

(1) 日月星辰(2) A B C D×9 × 4辰星月日 D C B A日＝，月＝，A＝，B＝，星＝，辰＝。

C＝，D＝。

10.在下面的□内填上合适的数字，使竖式成立。

(3) 3 (4) 634238 2星期五11.在HE＋HE＋HE＋HE＝AH的算式里，相同的字母表示相同的数字，不同的字母表示不同的数字。

第五周算式谜（一）专题简析：“算式谜”一般是指那些含有未知数字或缺少运算符号的算式。

解决这类问题，可以根据已学过的知识，运用正确的分析推理方法，确定算式中的未知数字和运用符号。

由于这类题目的解答过程类似全平时进行的猜谜语游戏，所以，我们把这类题目称为“算式谜题”。

解答算式谜问题时，要先仔细审题，分析数据之间的关系，找到突破口，逐步试验，分析求解，通常要运用倒推法、凑整法、估值法等。

1例1：在下面算式的括号里填上合适的数。

7 6 （） 5+ （） 4 7（）2 1 （）分析：根据题目特点，先看个位：7＋5=12，在和的个位（）中填2，并向十位进一；再看十位，（）+4+1的和个位是1，因此，第一个加数的（）中只能填6，并向百位进1；最后来看百位、千位，6+（）+1的和的个位是2，第二个加数的（）中只能填5，并向千位进1；因此，和的千位（）中应填8。

练习一（1）在括号里填上合适的数。

（2）在方框里填上合适的数。

6 （）（）□0 □□2+2（）1 5 －3（）1 7（）0 9 1 2 8 5 6 （3）下面的竖式里，有4个数字被遮住了，求竖式中被盖住的4个数字的和。

□□+ □□1 6 93例2：下面各式中“巨”、“龙”、“腾”、“飞”分别代表不同的数字，相同的汉字代表相同的数字。

当它们各代表什么数字时，下列的算式成立。

腾飞龙腾飞+巨龙腾飞2 0 0 1分析：先看个位，3个“飞”相加的和的个位数字是1，可推知“飞”代表7；再看十位，3个“腾”相加，再加上个位进来的2，所得的和的个位是0，可推知“腾”代表6；再看百位，两个“龙”相加，加上十位进上来的2，所得和的个位是0，“龙”可能是4或9，考虑到千位上的“巨”不可能为0，所以“龙”只能代表4，“巨”只能代表1。

4练习二（1） C D （2）式谜（3）澳门A C D 填式谜澳门归+A B C D +巧填式谜+庆澳门归1 9 8 9 1 9 9 5 1 9 9 95例3：下面各式中的“兵”、“炮”、“马”、“卒”各代表0—9这十个数字中的某一个，相同的汉字代表相同的数字。

（二年级）暑期备课教员：×××第一讲算式谜（一）一、教学目标： 1. 认真分析算式的特点，充分运用加、减法之间的关系，巧妙地安排每一个数。

2.了解加减法算式的结构，能从不同的角度分析、寻找算式谜的突破口，更快地找出要填的数字。

3.能正确理解题意，弄清题目特征，找准已知数字和所缺数字的关系。

4.通过填数练习，提高学生分析问题和解决问题的能力，对数学的兴趣也得到提升。

二、教学重点：分析算式中所包含的数量关系。

三、教学难点：找准突破口，快速而准确的找出答案。

四、教学准备：PPT五、教学过程：第一课时（50分钟）一、导入（5分)师：同学们，你们看过《西游记》吗？生：看过师：唐僧师徒四人在取经的路上，他们遇到了不少困难，不过，他们勇于挑战困难，善于思考，最后取得了胜利；据说他们到了西天之后，如来佛把佛经放在了一座很高很高的山顶上，还在路上设了五关考验他们，这五关可有趣了，包含着许多数学知识，你们愿意去挑战一下吗？生：愿意。

师：好，准备开始了，我们一起来看看第一关是什么？二、探索发现授课（40分）（一）例题一：（13分）根据算式，推算出每个图形所代表的数。

（1） 1 4+ □□=（）2 0（2） 1 5－△△=（）7师：我们来闯闯第一关，要走多少阶台阶才能到达半山腰？从山脚到半山腰有□=？层，每一层有△=？级台阶，我们来数一数有几个△，为了得出每层有多少阶台阶，我们来分组讨论！生：好。

师：真聪明，这么短的时间就解决了这个问题。

我们来看看下面这两个算式，这两个算式有意思吧！14+□=20，15-△=7，你们能不能求出方形图形和三角图形各代表几呢？生：老师，我知道，可以用20-14=6，所以方形图形等于6，也可以把6代入到竖式里，是14+6=20,所以□=6。

三角形就是用15-7=8，三角形等于8。

师：说得真是太棒了！其他同学明白了吗？生：明白了。

师：根据加法与减法之间的关系，先看个位。

算式谜（一）1 .在下面算式的括号里填上合适的数。

2 .在方框里填上合适的数。

1 .下面的竖式里，有4个数字被遮住了，求竖式中被盖住的4个数字的和。

3 .下面各式中“巨”、“龙”、“腾”、“飞”分别代表不同的数字，相同的汉字代表相同的数字。

当它们各代表什么数字时，下列的算式成立。

4 .下面各式中的“兵”、“炮”、“马”、“卒”各代表0—9这十个数字中的某一个，相同的汉字代表相同的数字。

这些汉字各代表哪些数字？5 .将0、1、2、3、4、5、6这七个数字填在圆圈和方格内，每个数字恰好出现一次，组成一个整数算式。

○×○=□=○÷○6 .将0、1、3、5、6、8、9这七个数字填在圆圈和方筐里，每个数字恰好出现一次组成一个整数算式。

○×○=□=○÷○7 .填入1、2、3、4、7、9，使等式成立。

□÷□=□÷□8 .用1、2、3、7、8这五个数字可以列成一个算式：（1+3）×7=28。

请你用0、1、2、3、4、6这六个数字列成一个算式。

9 .把“＋、－、×、÷”分别放在适当的圆圈中（运算符号只能用一次），并在方框中填上适当的数，使下面的两个等式成立。

36○0○15=15 21○3○5=□10 .把“＋、－、×、÷”分别填入下面的圆圈中，并在方框中填上适当的整数，使下面每组的两个等式成立。

①9○13○7=100 14○2○5=□② 17○6○2=100 5○14○7=□11 .将1～9这九个数字填入□中（每个数字只能用一次），组成三个等式。

□＋□=□□－□=□□×□=□。

第一讲《算式谜》（必做与选做）1.在下面算式□里，填上合适的数字，使算式成立，积是（）。

A. 3210B. 2340C. 2350D. 2310解析：6□×5＝33□，左边方框可填6或7，而又6□×3＝1□8，可以得出6□＝66 66×35＝2310。

所以选D。

2.在下面算式□里，填上合适的数字，使算式成立。

积是（）。

A. 1231B. 1431C. 1531D. 1631 解析：□＋5＝13(满10进1位，□＝8，□1＝81，2□×□＝81,27×3＝81或23×7＝81，所以第二个乘数的个位有3或7，（第二个乘数的十位×第一位乘数个位，积的尾数是5）□×□积的尾数是5,可以推出第二个乘数十位是5，讨论27×53＝1431与23×57＝1311，发现23×57＝1311不合题意舍去。

所以选B。

3.在下面算式□里，填上合适的数字，使算式成立。

这个两位数是（）。

A. 31B. 32C. 35D. 37解析：285乘一个一位数得到一个四位数，且这个四位数的千位是1，那么满足条件的只有4或5或6或7，再结合这个四位数十位上是2，可知道这个一位数是5，285×5＝1425，由285×□积为三位数，□里只能填1或2或3，再由百位上是9，推出□里是3 。

算式为285×35＝9975 所以两位数是35。

所以选C。

4.在下面算式□里，填上合适的数字，使算式成立。

这个三位数乘数是（）。

A. 787B. 887C. 897D. 987解析：从□8□×5＝4□35，80×5＝400，而积的最后两位是35，从而推出第一个乘数的个位是7，又因为7×□（第二个乘数十位）的积末尾是4，推出第二个乘数十位是2，即第二个乘数是25，□87×5＝4□35，第一个乘数百位是8或9，又因为□87×2＝17□4，所以第一个乘数百位只有8。

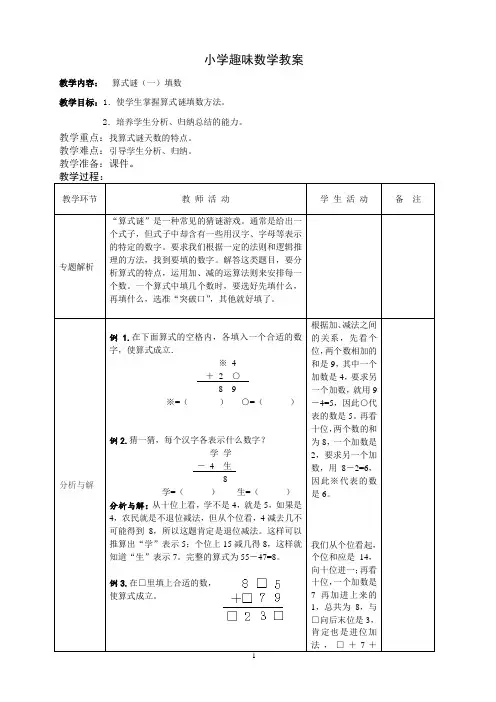
小学趣味数学教案教学内容：算式谜（一）填数教学目标：1．使学生掌握算式谜填数方法。

2．培养学生分析、归纳总结的能力。

教学重点：找算式谜天数的特点。

教学难点：引导学生分析、归纳。

教学准备：课件。

教学过程：教学环节教师活动学生活动备注专题解析“算式谜”是一种常见的猜谜游戏。

通常是给出一个式子，但式子中却含有一些用汉字、字母等表示的特定的数字。

要求我们根据一定的法则和逻辑推理的方法，找到要填的数字。

解答这类题目，要分析算式的特点，运用加、减的运算法则来安排每一个数。

一个算式中填几个数时，要选好先填什么，再填什么，选准“突破口”，其他就好填了。

分析与解例 1.在下面算式的空格内，各填入一个合适的数字，使算式成立．※4＋2 ○8 9※=（）○=（）例2.猜一猜，每个汉字各表示什么数字？学学－4 生8学=（）生=（）分析与解：从十位上看，学不是4，就是5，如果是4，农民就是不退位减法，但从个位看，4减去几不可能得到8，所以这题肯定是退位减法。

这样可以推算出“学”表示5；个位上15减几得8，这样就知道“生”表示7。

完整的算式为55－47=8。

例3.在□里填上合适的数，使算式成立。

根据加、减法之间的关系，先看个位，两个数相加的和是9，其中一个加数是4，要求另一个加数，就用9－4=5，因此○代表的数是5。

再看十位，两个数的和为8，一个加数是2，要求另一个加数，用8－2=6，因此※代表的数是6。

我们从个位看起，个位和应是14，向十位进一；再看十位，一个加数是7再加进上来的1，总共为8，与□向后末位是3，肯定也是进位加法，□＋7＋1例 4.在下面□里填上数字，使算式成立。

先看个位数，6减7不够减，向十位退1，和个位6合起来是16，16－7，个位□里填9。

再看十位数，□－9=3，□应为12，被个位退1，□里的值为13，因此十位方框应填3，并且向百位退一。

再看百位上的数，差是4，被减数百位上的2被十位上退掉1，还剩1，肯定要向千位退1，合成11才够减，11－□=4，□为7。

（三年级）暑期 备课教员：* * * 第三讲 算式谜（一）一、教学目标： 1. 会分析算式中所包含的数量关系，能找出隐蔽条件，选择有特征的部分作出局部判断。

2. 会利用列举和筛选结合的方法，逐步排除不合理的数字。

3. 试验时，能借助估值的方法，以缩小所求数字的取值范围， 达到快速而准确的目的；4. 算式谜解出后，知道要验算一遍。

二、教学重点： 找出隐蔽条件，利用列举和筛选相结合方法。

三、教学难点： 列举和筛选方法。

四、教学准备： PPT 五、教学过程：第一课时（50分钟）一、创设情景，激情导入（5分) 师：今天给大家讲一个故事： 小淘气一天，小淘气跑到爸爸的书房，想看看他的工程师爸爸天天都在忙什么，结果不小心把一瓶墨水碰洒了，这下可把小淘气吓坏了，仔细一看，墨水把一道写着算式的一些数字涂上了，怎么办呢？小淘气冥思苦想后，他推算出了所有被墨水涂上的数字。

爸爸回来后，不但没有批评他，还说他是个爱思考的好孩子。

师：小朋友们你们想知道是什么算式吗？ 生：想。

师：（出示算式）那就让我们一起来看一下吧！生：……师：大家知道这是什么吗？ 生：算式谜。

师：是的，今天这节课我们就一起来学习算式谜（板书——算式谜（一）） 师：那大家会不会算呢？ 生：……师：我们就一起去看看吧！ 二、探索发现授课（40分） （一）例题一：（13分） 在□内填入合适的数字，使竖式成立。

16 5+9 1+1师：同学们，我们先看一下这两个算式，说一说你想说什么？生：……师：第一个算式你是怎么想的？生：我们可以先找出它的突破口。

师：谁来说一下第一小题的突破口在哪？生：在个位。

师：怎么算呢？生1：已知一个加数的个位是6，还知道和的个位是5，可以求出第一个加数个位上的方框中填9。

生2：因为（9）+6=15，向十位进1，个位上是5，所以个位上方框填9。

师：很好，我们再来看哪一位？生：再来看十位。

师：是的，十位上又怎么填呢？生：十位上有一个加数是1及个位进的1，而和是一个四位数，所以我们要考虑到十位上要有进位。

四年级奥数举一反三第五周算式谜【一】专题简析；“算式谜”一般是指那些含有未知数字或缺少运算符号的算式。

解决这类问题，可以根据已学过的知识，运用正确的分析推理方法，确定算式中的未知数字和运用符号。

由于这类题目的解答过程类似全平时进行的猜谜语游戏，所以，我们把这类题目称为“算式谜题”。

解答算式谜问题时，要先仔细审题，分析数据之间的关系，找到突破口，逐步试验，分析求解，通常要运用倒推法、凑整法、估值法等。

例1；在下面算式的括号里填上合适的数。

76 【】 5+ 【】 4 7【】2 1 【】分析；根据题目特点，先看个位；7＋5=12，在和的个位【】中填2，并向十位进一；再看十位，【】+4+1的和个位是1，因此，第一个加数的【】中只能填6，并向百位进1；最后来看百位、千位，6+【】+1的和的个位是2，第二个加数的【】中只能填5，并向千位进1；因此，和的千位【】中应填8。

练习一（1）在括号里填上合适的数。

【2】在方框里填上合适的数。

6 【】【】□0 □□+2【】1 5 －3【】1 7【】0 9 1 2 8 5 6【3】下面的竖式里，有4个数字被遮住了，求竖式中被盖住的4个数字的和。

□□+ □□1 6 9例2；下面各式中“巨”、“龙”、“腾”、“飞”分别代表不同的数字，相同的汉字代表相同的数字。

当它们各代表什么数字时，下列的算式成立。

腾飞龙腾飞+巨龙腾飞2 0 0 1分析；先看个位，3个“飞”相加的和的个位数字是1，可推知“飞”代表7；再看十位，3个“腾”相加，再加上个位进来的2，所得的和的个位是0，可推知“腾”代表6；再看百位，两个“龙”相加，加上十位进上来的2，所得和的个位是0，“龙”可能是4或9，考虑到千位上的“巨”不可能为0，所以“龙”只能代表4，“巨”只能代表1。

练习二【1】 C D 【2】式谜【3】澳门A C D 填式谜澳门归+A B C D +巧填式谜+庆澳门归1 9 8 9 1 9 9 5 1 9 9 9例3；下面各式中的“兵”、“炮”、“马”、“卒”各代表0—9这十个数字中的某一个，相同的汉字代表相同的数字。

三年级奥数之算式谜算式谜1.在下面算式的□内，填上适当的数字，使算式成立。

解题思路：这是一道简单的加法题，只需要将两个数字相加即可得到答案。

因此，在□内填上数字2即可。

2.在□里填上适当的数，使算式成立。

解题思路：这是一道简单的乘法题，只需要将两个数字相乘即可得到答案。

因此，在□内填上数字5即可。

3.□里填哪些数字，可使这道除法算式成为一道完整的算式？解题思路：这是一道简单的除法题，只需要将被除数和除数相除即可得到商。

因此，在□内填上数字4和数字2即可。

4.在□里填上适当的数，使算式成立。

解题思路：这是一道简单的加法题，只需要将两个数字相加即可得到答案。

因此，在□内填上数字3即可。

5.在下面竖式的□里，各填入一个合适的数字，使算式成立。

解题思路：这是一道简单的加法题，只需要将两个数字相加即可得到答案。

因此，在第一个□内填上数字7，在第二个□内填上数字9即可。

6.□里可以填哪些数字？解题思路：这是一道简单的除法题，只需要将被除数和除数相除即可得到商。

因此，□内可以填任意数字。

7.在下面竖式的□里，各填入一个合适的数字，使算式成立。

解题思路：这是一道简单的加法题，只需要将两个数字相加即可得到答案。

因此，在第一个□内填上数字6，在第二个□内填上数字5即可。

8.在下面竖式的□里，各填入一个合适的数字，使算式成立。

解题思路：这是一道简单的乘法题，只需要将两个数字相乘即可得到答案。

因此，在第一个□内填上数字3，在第二个□内填上数字8即可。

9.在下面□中填入适当的数，使算式成立。

解题思路：这是一道简单的乘法题，只需要将两个数字相乘即可得到答案。

因此，在第一个□内填上数字2，在第二个□内填上数字4，在第三个□内填上数字3即可。

10.在下面□中填入适当的数，使算式成立。

解题思路：这是一道简单的除法题，只需要将被除数和除数相除即可得到商。

因此，在第一个□内填上数字6，在第二个□内填上数字7，在第三个□内填上数字5即可。