材料力学第五版(刘鸿文主编)课后答案
- 格式:ppt
- 大小:10.16 MB
- 文档页数:510
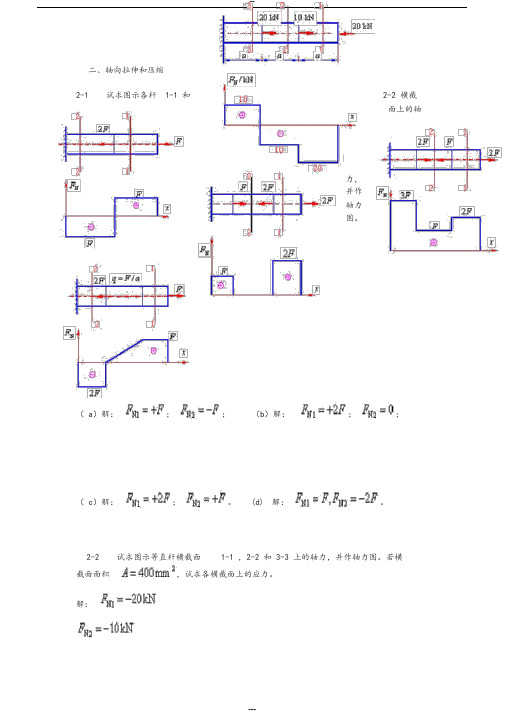
二、轴向拉伸和压缩2-1 试求图示各杆 1-1 和2-2 横截面上的轴力,并作轴力图。
( a)解:;;(b)解:;;( c)解:;。
(d) 解:。
2-2 试求图示等直杆横截面1-1 ,2-2 和 3-3 上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
解:返回1-1 ,2-2 和 3-3 2-3试求图示阶梯状直杆横截面上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
解:返回2-4 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个75mm×8mm的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和 EG横截面上的应力。
解:=1)求内力取 I-I 分离体得(拉)取节点 E 为分离体,故 (拉) 2) 求应力75 × 8等边角钢的面积 A2=11.5 cm( 拉 )(拉)返回2-5(2-6)图示拉杆承受轴向拉力,杆的横截面面积。
如以表示斜截面与横截面的夹角,试求当,30 ,45 ,60 ,90 时各斜截面上的正应力和切应力,并用图表示其方向。
解:返回2-6(2-8) 一木桩柱受力如图所示。
柱的横截面为边长 200mm的正方形,材料可认为符合胡克定律,其弹性模量 E=10 GPa。
如不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱的总变形。
解:(压)(压)返回2-7(2-9) 一根直径,其伸长为、长的圆截面杆,承受轴向拉力。
试求杆横截面上的应力与材料的弹性模量E。
解:2-8(2-11) 受轴向拉力 F 作用的箱形薄壁杆如图所示。
已知该杆材料的弹性常数为E,,试求 C 与D两点间的距离改变量。
解:横截面上的线应变相同因此返回2-9(2-12)图示结构中,AB为水平放置的刚性杆,杆,,材料相同,其1 2 3弹性模量 E ,已知,,,=210GPa。


[习题2-2]一打入基地内的木桩如图所示,杆轴单位长度的摩擦力f=kx**2,试做木桩的后力图。
解:由题意可得:33233110,,3/()3/(/)ll N fdx F kl F k F l F x Fx l dx F x l =====⎰⎰1有3[习题2-3] 石砌桥墩的墩身高m l 10=,其横截面面尺寸如图所示。
荷载kN F 1000=,材料的密度3/35.2m kg =ρ,试求墩身底部横截面上的压应力。
解:墩身底面的轴力为:g Al F G F N ρ--=+-=)( 2-3图)(942.31048.935.210)114.323(10002kN -=⨯⨯⨯⨯+⨯--=墩身底面积:)(14.9)114.323(22m A =⨯+⨯=因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。
MPa kPa m kNA N 34.071.33914.9942.31042-≈-=-==σ[习题2-7] 图示圆锥形杆受轴向拉力作用,试求杆的伸长。
2-7图解:取长度为dx 截离体(微元体)。
则微元体的伸长量为:)()(x EA Fdx l d =∆ ,⎰⎰==∆l l x A dxE F dx x EA F l 00)()( lxr r r r =--121,22112112d x l d d r x l r r r +-=+⋅-=,2211222)(u d x l d d x A ⋅=⎪⎭⎫ ⎝⎛+-=ππ,dx l d d du d x l d d d 2)22(12112-==+- du d d ldx 122-=,)()(22)(221212udu d d l du u d d lx A dx -⋅-=⋅-=ππ 因此,)()(2)()(202100u dud d E Fl x A dx E F dx x EA F l l l l⎰⎰⎰--===∆πlld x l d d d d E Fl u d d E Fl 011221021221)(21)(2⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--=⎥⎦⎤⎢⎣⎡-=ππ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+--=21221)(2111221d d l l d d d d E Fl π ⎥⎦⎤⎢⎣⎡--=122122)(2d d d d E Fl π214d Ed Fl π=[习题2-10] 受轴向拉力F 作用的箱形薄壁杆如图所示。

第16章厚壁圆简和旋转圆盘16.1 复习笔记一、厚壁圆筒厚壁圆筒的壁厚与半径属于同一量级,其几何和载荷都具对称性,因此,属于对称性问题。
对于厚壁圆筒的应力和变形的分析要综合考虑几何关系,静力平衡和物理三方面的关系。
在内压力p1和外压力p2作用下的厚壁圆筒,线弹性情况下,应力和变形分别为:1.应力径向应力:周向应力:2.变形筒壁内任一点的径向位移:二、等厚旋转圆盘对于以匀角速度 旋转的等厚圆盘,属于轴对称问题,其应力计算如下。
1.实心圆盘径向应力:周向应力:在圆盘中心,二者均达到最大值:2.有孔圆盘圆盘中心有半径为a的圆孔,径向应力和周向应力分别为:在处,有:在圆孔内边缘处,有:16.2 课后习题详解16.1 万能试验机油缸外径D=194 mm,活塞面积为0.01 m2。
F=200 kN。
试求油。
缸内侧面的应力,并求第三强度理论的相当应力3r图16-1解:根据题意,筒内径:故,圆筒所承受的内压力:3120010200.01F p MPA ⨯===,油缸内侧的应力:径向应力周向应力第三强度理论的相当应力3r σ:。
16.2 某型柴油机的连杆小头如图16-2所示。
小头外径d 3=50 mm ,内径d 2=39 mm 。
青铜衬套内径d 1=35 mm 。
连杆材料的弹性模量E=220 GPa ,青铜衬套的弹性模量E 1=115 GPa ,两种材料的泊松比皆为μ=0.3。
小头及铜衬套间的过盈量按直径计算为(0.068+0.037)mm ,其中0.068 mm 为装配过盈,0.037 mm 为温度过盈。
试计算小头与衬套间的压力。
图16-2解:根据题意,内外筒的参数如下: 内筒:,装配过盈量:外筒:,,则装配压力:16.3 炮筒内直径为150 mm ,外直径为250 mm 。
射击时筒内气体的最大压力为P 1=120 MPa 。
试求炮筒内侧面的周向应力及径向应力。
解:炮筒属于只有内压的情况,且1502507512522,====a mm b mm ,=75a mm ρ=,1=120MPa ρ。

材料力学第五版答案引言材料力学是研究材料在外力作用下力学性能变化规律的学科,通过对材料的形变、应力、应变等力学参数的研究,能够揭示材料的力学特性。
本文将对《材料力学第五版》中的习题答案进行整理和总结,以供学习和参考。
第一章弹性力学基本理论1.1 弹性力学的基本概念习题答案:弹性力学是一门研究材料在外力作用下发生弹性变形时,形变与应力之间的关系及各种外力引起材料体内产生的应变和应力分布规律的学科。
其基本概念包括:•弹性变形:材料在外力作用下发生的可恢复的形变。
•弹性体:能够经历弹性变形的材料。
•应变:材料的形变量,以单位长度的变化表示,分为正应变和剪应变。
•应力:材料的内外力分布情况,以单位面积的力表示,分为正应力和剪应力。
•弹性模量:衡量材料抵抗变形能力的指标,常用符号为E。
•泊松比:衡量材料横向膨胀与纵向收缩的比值,常用符号为ν。
1.2 弹性体的应力应变关系习题答案:弹性体的应力应变关系可以通过《材料力学第五版》中的应变能密度公式和胡克定律来描述。
具体公式如下:•应变能密度公式:$$\\sigma = \\dfrac{1}{2}E\\epsilon^2$$•胡克定律:$$\\sigma = E\\epsilon$$其中,$\\sigma$ 表示应力,E表示弹性模量,$\\epsilon$ 表示应变。
这两个公式可以互相推导,给出了应力和应变之间的关系。
1.3 杨氏模量和泊松比习题答案:杨氏模量和泊松比是描述材料力学性质的重要参数。
•杨氏模量(Young’s modulus):表示单位面积下材料沿着垂直方向的形变和应力之间的关系,常用符号为E。
•泊松比(Poisson’s ratio):表示材料横向膨胀和纵向收缩之间的比例关系,常用符号为E。
杨氏模量和泊松比的计算公式如下:•杨氏模量:$$E = \\dfrac{\\sigma}{\\epsilon}$$•泊松比:$$\ u = -\\dfrac{\\epsilon_\\perp}{\\epsilon_\\parallel}$$1.4 平面应力和平面应变习题答案:平面应力和平面应变是指材料中只发生在某一平面上的应力和应变。
