材料力学第五版(刘鸿文主编)课后答案2

材料力学第五版课后习题答案1. 弹性力学基本概念。

1.1 什么是应力？什么是应变？应力是单位面积上的内力，是描述物体内部受力情况的物理量；而应变则是物体单位长度的形变量，描述了物体在受力作用下的形变情况。

1.2 什么是胡克定律？胡克定律是描述弹性体在弹性变形范围内应力与应变成正比的关系，即应力与应变成线性关系。

1.3 什么是弹性模量？弹性模量是描述物体在受力作用下的变形程度的物理量，通常用E表示，单位是帕斯卡（Pa）。

2. 线弹性力学。

2.1 什么是轴向力？什么是轴向变形？轴向力是指作用在物体轴向的力，轴向变形是指物体在受到轴向力作用下的形变情况。

2.2 什么是泊松比？泊松比是描述物体在轴向受力作用下，横向变形与轴向变形之间的比值，通常用ν表示。

2.3 什么是弯曲应力？什么是弯曲变形？弯曲应力是指物体在受到弯矩作用下的内部应力情况，弯曲变形是指物体在受到弯矩作用下的形变情况。

3. 弹性力学的能量法。

3.1 什么是弹性势能？弹性势能是指物体在受力变形后，能够恢复原状时所具有的能量，通常用U表示。

3.2 什么是弹性线性势能？弹性线性势能是指物体在弹性变形范围内，弹性势能与形变量成线性关系的势能。

3.3 什么是弹性势能密度？弹性势能密度是指单位体积或单位质量物体所具有的弹性势能，通常用u表示。

4. 弹塑性力学。

4.1 什么是屈服点？屈服点是指物体在受力作用下，开始出现塑性变形的临界点。

4.2 什么是屈服应力？屈服应力是指物体在受力作用下开始发生塑性变形时所具有的应力大小。

4.3 什么是塑性势能？塑性势能是指物体在受到超过屈服应力的作用下，发生塑性变形所具有的能量。

5. 薄壁压力容器。

5.1 什么是薄壁压力容器？薄壁压力容器是指壁厚相对于容器直径而言很小的压力容器。

5.2 薄壁压力容器的内、外压力对容器的影响有哪些？内压力会使容器产生膨胀变形，而外压力会使容器产生收缩变形。

5.3 薄壁压力容器的应力分布情况是怎样的？薄壁压力容器内外表面的应力分布情况是不均匀的，通常集中在壁厚的两侧。

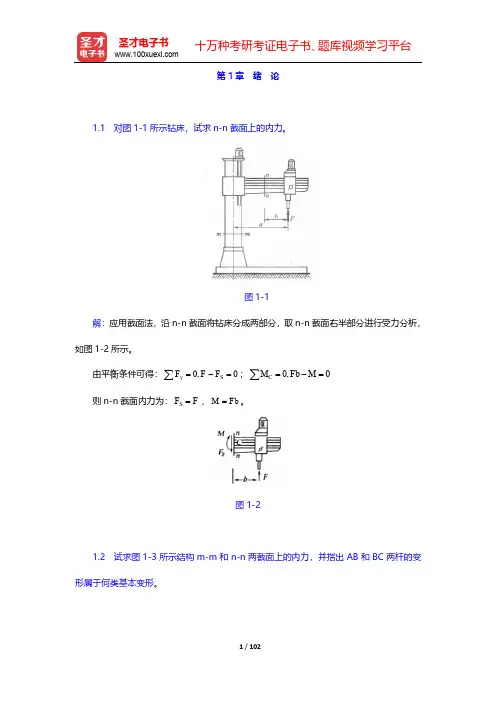
第1章 绪 论1.1 对图1-1所示钻床，试求n-n 截面上的内力。

图1-1解：应用截面法，沿n-n 截面将钻床分成两部分，取n-n 截面右半部分进行受力分析，如图1-2所示。

由平衡条件可得：0,0y S F F F =-=∑；0,0C M Fb M =-=∑则n-n 截面内力为：S F F =，M Fb =。

图1-21.2 试求图1-3所示结构m-m 和n-n 两截面上的内力，并指出AB 和BC 两杆的变形属于何类基本变形。

图1-3解：（1）应用截面法，取n-n 截面以下部分进行受力分析，如图1-4（a ）所示。

由平衡条件可得：0,3320A N M F =⨯-⨯=∑则截面内为：2N F kN =BC 杆属于拉伸变形。

（2）应用截面法，取m-m 截面右侧部分及n-n 截面以下部分进行受力分析，如图1-4（b ）所示。

由平衡条件可得：0,3310O N M F M =⨯-⨯-=∑；0,30y S N F F F =+-=∑则截面内为：1S F kN =，1M kN m =⋅AB 杆属于弯曲变形。

图1-41.3 在图1-5所示简易吊车的横梁上，F 力可以左右移动。

试求截面1-1和2-2上的内力及其最大值。

图1-5解：（1）应用截面法，取1-1截面以下部分进行受力分析，如图1-6（a ）所示。

由平衡条件可得：10,sin 0A N M F l Fx α=-=∑解得：1sin N Fx F l α= 故当x l =时，1-1截面内力有最大值：1max sin N F F α=。

（2）应用截面法，取1-1截面以下，2-2截面右侧部分进行受力分析，如图1-6（b ）所示。

由平衡条件可得：210,cos 0x N N F F F α=-=∑210,sin 0y S N F F F F α=--=∑()120,sin 0O N M F l x M α=--=∑解得2-2截面内力：2cot N Fx F l α=，21S x F F l ⎛⎫=- ⎪⎝⎭，()2x l x M F l -= 综上可知，当x l =时，2N F 有最大值，且2max cot N F F α=；当0x =时，2S F 有最大值，且2max S F F =；当2l x =时，弯矩2M 有最大值，且2max 4Fl M =。

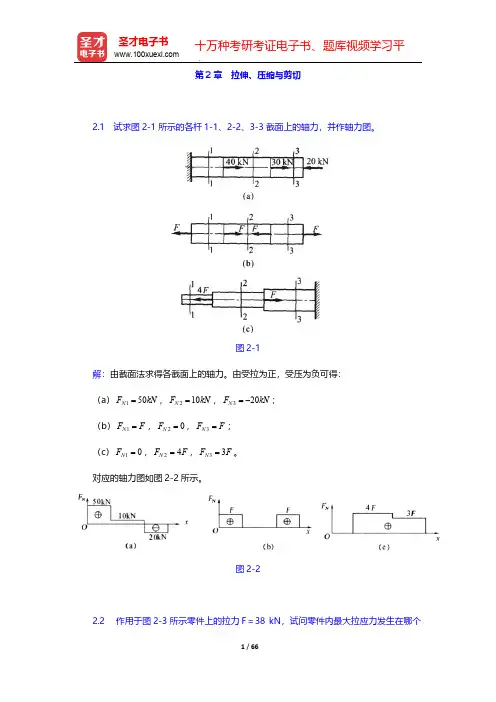
第2章　拉伸、压缩与剪切2.1 试求图2-1所示的各杆1-1、2-2、3-3截面上的轴力，并作轴力图。

图2-1解：由截面法求得各截面上的轴力。

由受拉为正，受压为负可得：（a ），，；150N F kN =210N F kN =320N F kN =-（b ），，；1N F F =20N F =3N F F =（c ），，。

10N F =24N F F =33N F F =对应的轴力图如图2-2所示。

图2-22.2 作用于图2-3所示零件上的拉力F ＝38 kN ，试问零件内最大拉应力发生在哪个截面上?并求其值。

图2-3 图2-4解：由拉应力计算公式可知，轴力一定时，最大拉应力发生在横截面积最小截F Aσ=面上，如图2-4所示。

1-1截面的面积：2-2截面的面积：比较可知，最大拉应力发生在1-1截面，且。

2.3 在图2-1(c)中，若1-1、2-2、3-3三个截面的直径分别为：d1＝15 mm ，d2＝20 mm ，d3＝24 mm ，F ＝8 kN ，试用图线表示横截面上的应力沿轴线的变化情况。

解：由题2.1可知，三截面上的轴力分别为：，，。

10N F =24NF F =33N F F =则三个截面上的应力分别为故横截面上应力沿轴线分布如图2-5所示。

图2-52.4 在图2-6所示结构中，若钢拉杆BC 的横截面直径为10 mm ，试求拉杆内的应力。

设由BC 连接的1和2两部分均为刚体。

图2-6解：将结构在节点A 处断开，分别对两部分进行受力分析，如图2-7所示。

图2-7根据平衡条件可得：则BC 杆的轴力为：故拉杆BC 的应力为：。

2.5 图2-8所示结构中，1，2两杆的横截面直径分别为10 mm 和20 mm 。

试求两杆内的应力。

设两根横梁皆为刚体。

图2-8图2-9解：对刚性横梁AB 进行受力分析，如图2-9所示。

静力平衡方程：解得：故1、2两杆的应力分别为。

2.6 直径为10 mm 的圆杆，在拉力F ＝10 kN的作用下，试求最大切应力，并求出木杆的横截面夹角为α＝30°的斜截面上正应力及切应力。

5[习题2-2]一打入基地内的木桩如图所示，杆轴单位长度的摩擦力f=kx**2，试做木桩的后力图。

解：由题意可得：33233110,,3/()3/(/)ll N fdx F kl F k F l F x Fx l dx F x l =====⎰⎰1有3[习题2-3] 石砌桥墩的墩身高m l 10=，其横截面面尺寸如图所示。

荷载kN F 1000=，材料的密度3/35.2m kg =ρ，试求墩身底部横截面上的压应力。

解：墩身底面的轴力为：g Al F G F N ρ--=+-=)( 2-3图)(942.31048.935.210)114.323(10002kN -=⨯⨯⨯⨯+⨯--=墩身底面积：)(14.9)114.323(22m A =⨯+⨯=因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

MPa kPa mkNA N 34.071.33914.9942.31042-≈-=-==σ[习题2-7] 图示圆锥形杆受轴向拉力作用，试求杆的伸长。

2-7图解：取长度为dx 截离体（微元体）。

则微元体的伸长量为：)()(x EA Fdx l d =∆ ，⎰⎰==∆l l x A dxE F dx x EA F l 00)()(l xr r r r =--121，22112112d x l d d r x l r r r +-=+⋅-=，2211222)(u d x ld d x A ⋅=⎪⎭⎫ ⎝⎛+-=ππ，dx l d d du d x l d d d 2)22(12112-==+- du d d l dx 122-=，)()(22)(221212udud d l du u d d lx A dx -⋅-=⋅-=ππ因此，)()(2)()(202100u dud d E Fl x A dx E F dx x EA F l l l l⎰⎰⎰--===∆π lld x l d d d d E Fl u d d E Fl 011221021221)(21)(2⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--=⎥⎦⎤⎢⎣⎡-=ππ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+--=21221)(2111221d d l l d d d d E Fl π ⎥⎦⎤⎢⎣⎡--=122122)(2d d d d E Fl π214d Ed Flπ=[习题2-10] 受轴向拉力F 作用的箱形薄壁杆如图所示。