一种基于时间分割法和数字积分法混合实现的空间直线插补方法_刘宜
- 格式:pdf
- 大小:670.75 KB
- 文档页数:5

基于曲线插补的多轴联动交叉耦合控制方法赵国勇;赵玉刚【摘要】针对高精度轮廓跟踪需要,将曲线插补和交叉耦合控制器结合起来进行研究。
在每个采样周期根据各轴反馈的实际刀具位置与插补缓冲区中存储的一定数量的插补点,研究了一种"三点圆弧法"轮廓误差计算模型,并研究了轮廓误差补偿修正量计算及分配方法。
在数控试验台上跟踪一段三次非均匀有理B样条轮廓曲线,对比试验表明,所提出的基于曲线插补的轮廓误差交叉耦合控制方法能够有效减小轮廓误差,获得更高轮廓精度。
%Aiming at the tracking demand of high precision contour,the cross-coupled controller integrated with curve interpolation was studied.According to the real cutter positions from each axis feedback and the interpolation dots stored in the interpolation buffer in every sampling period,a "three-point arc approach" contour error computing model was developed.Moreover,the contour error compensated correction quantity computation and distribution approach was put forward.A cubic Non-Uniform Rational B-Spline Curve(NURBS)profile curve on the numerial control experiment table was tracked.The experiment results showed that the developed contour error cross-coupled control approach based on curve interpolation could effectively reduce contour error and obtain satisfactory contour precision.【期刊名称】《计算机集成制造系统》【年(卷),期】2011(017)009【总页数】5页(P1968-1972)【关键词】曲线插补;交叉耦合控制;轮廓误差;补偿修正量;机床【作者】赵国勇;赵玉刚【作者单位】山东理工大学精密制造与特种加工省级重点实验室,山东淄博255049;山东理工大学精密制造与特种加工省级重点实验室,山东淄博255049【正文语种】中文【中图分类】TH13数控机床轮廓精度的提高与机床各进给轴的动态特性是否匹配密切相关。

时间分割插补法的原理以时间分割插补法的原理为标题,写一篇文章。
时间分割插补法(Time Division Interpolation,简称TDI)是一种用于处理遥感影像数据的插值算法。
它可以根据遥感卫星的轨道和观测时间信息,对不同时间的影像进行插值,从而得到连续时间序列的影像数据。
在遥感影像处理中,常常需要获取连续的时间序列影像数据,以便进行时间序列分析、监测和变化检测等应用。
然而,由于各种原因,遥感卫星的观测时间间隔可能并不均匀,这就导致了获取连续时间序列影像数据的困难。
时间分割插补法就是为了解决这一问题而提出的。
时间分割插补法的基本原理是将时间分割成若干个时间段,并对每个时间段内的影像数据进行插值。
具体而言,首先根据遥感卫星的观测时间信息,将整个时间序列划分为多个时间段,每个时间段内的影像数据可以认为是均匀分布的。
然后,对于每个时间段内的影像数据,可以利用插值算法进行插值,得到该时间段内的连续影像数据。
常用的插值算法包括线性插值、双线性插值、三次样条插值等。
线性插值是最简单的插值算法,它通过线性关系来估计插值点的像素值。
双线性插值则考虑了邻近像素的权重,根据距离插值点的距离来确定权重,从而提高了插值的精度。
三次样条插值则通过三次多项式来拟合插值点附近的像素值,从而得到更加平滑的插值结果。
在时间分割插补法中,不同时间段内的插值结果需要进行无缝拼接,以得到整个时间序列的连续影像数据。
这就需要考虑到邻近时间段的边界像素,在进行插值时要保持边界像素的连续性。
一种常用的方法是通过加权平均来实现边界像素的插值,即将邻近时间段内的插值结果按照一定权重进行加权平均,从而得到边界像素的插值结果。
时间分割插补法在遥感影像数据处理中具有重要的应用价值。
它可以帮助我们获取连续时间序列的影像数据,从而实现对地表变化的监测和分析。
例如,在农业领域,可以利用时间分割插补法获取不同时间段内的农田影像数据,以监测农作物的生长情况和变化趋势。


DOI: 10.3969/J.ISSN.2097-3764.2024.01.016Vol. 19 No.01 March, 2024第 19 卷 第1期 2024 年 3 月/复杂地层结构三维地质建模空间插值方法研究郑杨,简季(成都理工大学地球科学学院,四川 成都 610059)摘 要:三维地质体对于自然资源勘探、环境保护、自然灾害风险评估等领域都具有重要意义。
在建模过程中,地质体的模型精度与插值算法有着直接关系。
为研究不同插值算法的适用情况,文章对云南陆良某污染场地进行浅层三维地质建模,分别选取反距离权重法和自然邻域法,利用钻孔数据插值建模,并对模型结果进行目视检验和误差对比分析。
研究结果表明:反距离权重法适用范围广,建模精度较高;相较于自然邻域法,反距离权重法更适用于地层结构复杂的三维地质建模,该方法对断层细节的描述更细致,模型更符合实际情况;而自然邻域法在断层明显的区域插值效果较差,不适用于地层结构复杂的情况。
关键词:三维地质模型;钻孔数据;反距离权重法;自然邻域法;精度验证Spatial interpolation methods for 3D geological modeling ofcomplex strata structuresZHENG Yang, JIAN Ji(School of Earth Sciences, Chengdu University of Technology, Chengdu 610059, Sichuan, China )Abstract: Three-dimensional (3D) geological bodies are of great significance in natural resources exploration, environmental protection, natural disaster risk assessment, and other fields. In the modeling process, the accuracy of geological body models is directly related to interpolation algorithms. T o study the applicability of different interpolation algorithms, this paper con-ducted shallow 3D geological modeling in a heavy metal pollution area in Luliang, Yunnan. The inverse distance weighting method and natural neighborhood method were selected to interpolate the drilling data in the study area. Visual inspection and error comparison were carried out of the model results. The results show that the inverse distance weighting method has a wider applicability range and higher modeling accuracy. Compared to the natural neighborhood method, the inverse dis-tance weighting method is more suitable for complex geological modeling with distinct stratigraphic structures, providing a more detailed description of fault details and a model that better reflects reality. On the other hand, the natural neighbor-hood method has poor interpolation performance in areas with distinct faults and is not suitable for complex stratigraphic structures.Keywords: 3D geological model; drill data; inverse distance weighting method; natural neighborhood method; accuracy verifica-tion收稿日期:2023-09-05;修回日期:2023-11-16第一作者简介:郑杨(1990- ),男,在读硕士研究生,研究方向:数字孪生与三维建模。

dda数字积分插补算法DDA(Digital Differential Analyzer)数字积分插补算法是计算机图形学中常用的一种直线段插值算法。
它的主要作用是根据给定的两个端点坐标,通过在直线上等间距采样的方式,计算出直线上各个点的坐标值,从而实现直线的平滑插值。
DDA算法的基本思想是利用直线的斜率来逐步逼近直线的路径,从而计算出直线上各个点的坐标。
具体步骤如下:1. 计算出直线的斜率k,即直线在x轴上的单位增量Δx与在y轴上的单位增量Δy的比例:k = Δy / Δx。
2. 选择直线上两个端点中x值较小的一个作为起始点,并以其坐标值(x0,y0)作为起始值。
3. 将起始点的坐标值作为当前点的坐标值,并将其绘制到屏幕上。
4. 通过递增x坐标值的方式,计算出下一个点的y坐标值,即y = y0 + k。
5. 将下一个点的坐标值(x0+1,y)作为当前点的坐标值,并将其绘制到屏幕上。
6. 重复步骤4和步骤5,直到达到直线的结束点。
通过以上步骤,可以得到直线上各个点的坐标值,从而实现直线的平滑插值。
DDA算法的优点是计算简单、速度快,适用于直线斜率变化不大的情况。
但由于采用等间距采样的方式,可能导致插值结果与实际直线存在误差。
为了更好地理解DDA算法的原理,下面以一个具体的例子来说明。
假设有两个端点坐标分别为(2,2)和(8,5),我们来计算出直线上各个点的坐标。
计算出直线的斜率k = (5-2) / (8-2) = 3/6 = 1/2。
然后,选择起始点(2,2)作为起始值,并将其绘制到屏幕上。
接下来,通过递增x坐标值的方式,依次计算出下一个点的y坐标值。
根据步骤4,我们可以得到以下结果:x | y--------2 | 23 | 2 + 1/2 = 2.54 | 2.5 + 1/2 = 35 | 3 + 1/2 = 3.56 | 3.5 + 1/2 = 47 | 4 + 1/2 = 4.58 | 4.5 + 1/2 = 5我们得到直线上各个点的坐标值为(2,2)、(3,2.5)、(4,3)、(5,3.5)、(6,4)、(7,4.5)和(8,5)。

数字积分法插补仿真实验教学系统开发作者:杨泽青张俊峰刘丽冰肖艳军杨伟东张艳蕊来源:《科技视界》2016年第18期【摘要】为便于学生直观地理解数字积分法插补原理和插补流程,采用LabVIEW构建了虚拟仿真实验教学平台。
该平台集成了直线插补模块和圆弧插补模块,每个模块主要包括插补运算初始化启动功能、插补速度控制功能和插补过程实时显示功能,便于学生形象直观地模拟单象限及跨象限直线和圆弧插补过程,进而深刻理解数字积分法插补原理,同时也为数字积分法插补算法的改进和功能拓展提供相应接口,为学生创新性实验开展提供平台支撑。
【关键词】数控插补;数字积分法;虚拟仿真;实验教学;教学平台1 数控插补实验教学存在问题及解决思路数字积分法插补算法、插补原理是《计算机数控技术》最重要的一部分教学内容。
实物实验教学存在数控设备短缺、实验地点和实验时间受限等不足,学生只能在限定的时间内完成规定的实验操作,不利于培养学生的自主创新能力,虚拟仿真实验教学恰好弥补了这一不足。
鉴于LabVIEW具有可视化的编程环境和流程图式的编程风格、内置高效的程序编译器、灵活的程序调试手段、功能强大的数据处理和分析函数库等特点,为增强实验教学内容的实践性和交互性,本文采用LabVIEW开发数字积分法插补仿真实验平台,充分拓展实验教学的内容、形式、空间与时间,使学生在对插补算法感性认识的基础上进一步深化所学知识,理解数字积分法插补原理的精髓所在,增强实验教学的灵活性和生动性;而且通过拓展接口引导学生进行算法的改进,培养学生的自主研发能力和工程创新能力,使教学和科研有机地结合起来。
2 数控插补虚拟仿真教学平台的功能需求分析插补是数控系统的重要功能,教师在讲授该部分内容时,希望学生在对插补概念及插补原理理解的基础上,深刻体会插补的流程及零件数控加工的实质内涵,虚拟仿真教学平台的主要功能是用来辅助课堂教学,不仅能形象生动地模拟单象限直线和圆弧插补,而且能实现跨象限的直线和圆弧插补功能,提高插补流程的直观性和真实性,便于学生形象地获取知识、激发学习热情,取得较好的教学效果。
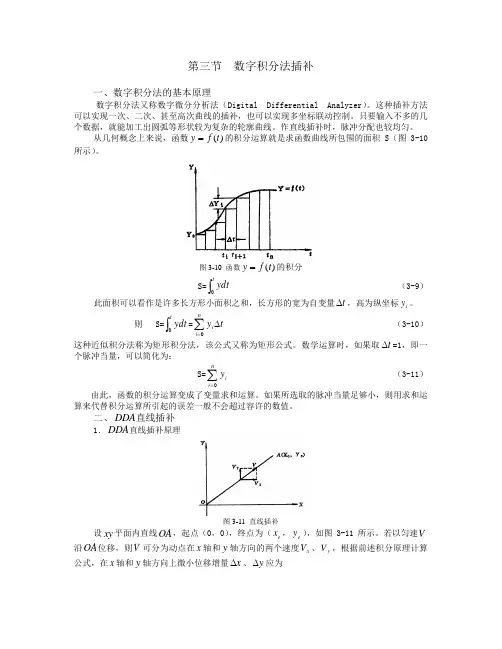
第三节 数字积分法插补一、数字积分法的基本原理数字积分法又称数字微分分析法(Digital Differential Analyzer )。
这种插补方法可以实现一次、二次、甚至高次曲线的插补,也可以实现多坐标联动控制。
只要输入不多的几个数据,就能加工出圆弧等形状较为复杂的轮廓曲线。
作直线插补时,脉冲分配也较均匀。
从几何概念上来说,函数)(t f y =的积分运算就是求函数曲线所包围的面积S (图3-10所示)。
图3-10 函数)(t f y =的积分S=⎰tydt 0(3-9)此面积可以看作是许多长方形小面积之和,长方形的宽为自变量t ∆,高为纵坐标i y 。
则 S=⎰tydt 0=t y ni i ∆∑=0(3-10)这种近似积分法称为矩形积分法,该公式又称为矩形公式。
数学运算时,如果取t ∆=1,即一个脉冲当量,可以简化为:S=∑=ni iy(3-11)由此,函数的积分运算变成了变量求和运算。
如果所选取的脉冲当量足够小,则用求和运算来代替积分运算所引起的误差一般不会超过容许的数值。
二、DDA 直线插补 1.DDA 直线插补原理图3-11 直线插补设xy 平面内直线OA ,起点(0,0),终点为(e x ,e y ),如图3-11所示。
若以匀速V 沿OA 位移,则V 可分为动点在x 轴和y 轴方向的两个速度x V 、y V ,根据前述积分原理计算公式,在x 轴和y 轴方向上微小位移增量x ∆、y ∆应为⎩⎨⎧∆=∆∆=∆t V y tV x y x (3-12) 对于直线函数来说,x V 、y V ,V 和L 满足下式⎪⎪⎩⎪⎪⎨⎧==L y VV Lx V V e y e x 从而有⎩⎨⎧==e yex ky V kx V (3-13) 其中:LVk =因此坐标轴的位移增量为⎩⎨⎧∆=∆∆=∆tky y tkx x e e (3-14) 各坐标轴的位移量为⎪⎪⎩⎪⎪⎨⎧∆==∆==⎰∑⎰∑==tn i e e t n i e e ty k dt ky y t x k dt kx x 0101(3-15) 所以,动点从原点走向终点的过程,可以看作是各坐标轴每经过一个单位时间间隔t ∆,分别以增量e kx 、e ky 同时累加的过程。


DDA插补的高级语言实现The Realization of DDA Interpolation In Advanced Computer Languaget王健强摘要:DDA(数字积分法)是开环数控系统常用的插补方法,文中主要分析、讨论直线和圆弧DDA插补的高级语言(C++语言)实现算法和技巧。
用半加载法和极值比较法对DDA法进行修正,有效地提高了圆弧DDA法的插补精度。
关键词:DDA插补C++语言软件插补Abstract:DDA Interpolation is a commonly used method of in terpolation.The algori thm and mechanics of DDA Interpo-lati on of line and arc in advanced computer language is mainly discussed and analyzed.The precision of Interpolation is im-proved by means of the method of half Load and the method of comparison of maxi mu m.Keywords:DDA Interpolation Advanced Computer Language Software Interpolation1引言随着计算机技术和微电子技术的迅猛发展,数控机床在现代机械加工业中已占有越来越大的比重。
近年来,以IPC(PC总线工控机)为控制主机的机床数控系统正以前所未有的速度发展,其性能稳定、可靠的各种类型的功能接口模板几乎应有尽有,这无疑为IPC的应用提供了坚实的硬件保障:同时又降低了硬件开发成本。
自从微机进入数控领域后,硬件数控正在被软件数控C NC所代替,其中包括数控系统重要的插补功能的代替。
众所周知,数控机床的运动(直线、圆弧等)通过插补实现。

关于序列二次规划(SQP)算法求解非线性规划问题研究兰州大学硕士学位论文关于序列二次规划(SQP)算法求解非线性规划问题的研究姓名:石国春申请学位级别:硕士专业:数学、运筹学与控制论指导教师:王海明20090602兰州大学2009届硕士学位论文摘要非线性约束优化问题是最一般形式的非线性规划NLP问题,近年来,人们通过对它的研究,提出了解决此类问题的许多方法,如罚函数法,可行方向法,Quadratic及序列二次规划SequentialProgramming简写为SOP方法。
本文主要研究用序列二次规划SOP算法求解不等式约束的非线性规划问题。
SOP算法求解非线性约束优化问题主要通过求解一系列二次规划子问题来实现。
本文基于对大规模约束优化问题的讨论,研究了积极约束集上的SOP 算法。
我们在约束优化问题的s一积极约束集上构造一个二次规划子问题,通过对该二次规划子问题求解,获得一个搜索方向。
利用一般的价值罚函数进行线搜索,得到改进的迭代点。
本文证明了这个算法在一定的条件下是全局收敛的。
关键字:非线性规划,序列二次规划,积极约束集Hl兰州人学2009届硕二t学位论文AbstractNonlinearconstrainedarethemostinoptimizationproblemsgenericsubjectsmathematicalnewmethodsareachievedtosolveprogramming.Recently,Manyasdirectionit,suchfunction,feasiblemethod,sequentialquadraticpenaltyprogramming??forconstrainedInthisthemethodspaper,westudysolvinginequalityabyprogrammingalgorithm.optimizationproblemssequentialquadraticmethodaofSQPgeneratesquadraticprogrammingQPsequencemotivationforthisworkisfromtheofsubproblems.OuroriginatedapplicationsinanactivesetSQPandSQPsolvinglarge-scaleproblems.wepresentstudyforconstrainedestablishontheQPalgorithminequalityoptimization.wesubproblemsactivesetofthesearchdirectionisachievedQPoriginalproblem.AbysolvingandExactfunctionsaslinesearchfunctionsubproblems.wepresentgeneralpenaltyunderobtainabetteriterate.theofourisestablishedglobalconvergencealgorithmsuitableconditions.Keywords:nonlinearprogramming,sequentialquadraticprogrammingalgorithm,activesetlv兰州大学2009届硕士学位论文原创性声明本人郑重声明:本人所呈交的学位论文,是在导师的指导下独立进行研究所取得的成果。
时间分割插补法的原理
时间分割插补法是指在控制系统中,将所需的控制信号按照时间分段的方式进行插补计算,从而实现平滑的运动控制。
其原理主要包括以下几个步骤:
1. 目标路径生成:根据设定的起点和终点,计算出路径函数,即描述运动变化的函数。
2. 时间分割:将整个运动过程分割成若干个时间段。
时间段的长度可以根据需要进行设定,一般情况下,长度越短,插补的精度越高。
3. 插补计算:对每个时间段进行插补计算,根据路径函数和时间段长度,计算出每个时间点上的位置、速度和加速度。
4. 控制命令生成:根据插补计算的结果,生成相应的控制命令,包括位置命令、速度命令和加速度命令。
5. 控制执行:根据生成的控制命令,控制执行器(如伺服电机)进行相应的运动控制,使得实际运动与期望运动一致。
通过时间分割插补法,可以实现平滑的运动轨迹控制,并且能够避免速度和加速度的突变,从而提高系统的稳定性和精度。
同时,插补计算的精度可以通过时间段长度的调整来进行控制,以满足不同应用的需求。
数控原理与系统课程设计课题名称:数字积分插补法直线插补专业:班级:姓名:指导老师:数控原理与系统课程设计任务书班级姓名学号课程设计的目的1)了解连续轨迹控制数控系统的组成原理。
2) 掌握数字积分插补的基本原理。
3)掌握数字积分插补的软件实现方法。
二、课程设计的任务数字积分法又称数字微分分析法DDA(Digital Differential Analyzer)。
数字积分法具有运算速度快、脉冲分配均匀、易于实现多坐标联动及描绘平面各种函数曲线的特点,应用比较广泛。
其缺点是速度调节不便,插补精度需要采取一定措施才能满足要求。
由于计算机有较强的计算功能和灵活性,采用软件插补时,上述缺点易于克服。
本次课程设计具体要求如下:1)数字积分插补法基本原理2)数字积分插补法插补软件流程图3)算法描述(逐点比较法算法在VB中的具体实现)4)编写算法程序清单5)软件运行仿真效果二、课程设计报告要求1)按课程设计任务5点要求为标题,编写课程设计报告,最后加一点:此次课程设计小结(包括设计过程中所碰到的问题、解决办法以及有关设计体会等)。
2)字数在3000字左右。
3)仿真软件一份。
三、学生分组学 生 姓 名数控原理与系统课程设计说明书一、数字积分法直线插补的基本原理数字积分法是利用数字积分的方法,计算刀具沿各坐标轴的位移,使得刀具沿着所加工的轮廓曲线运动利用数字积分原理构成的插补装置称为数字积分器,又称数字微分分析器(Digital Differential Analyzer ),简称DDA 。
数字积分器插补的最大优点在于容易实现多坐标轴的联动插补、能够描述空间直线及平面各种函数曲线等。
因此,数字积分法插补在轮廓数控系统中得到广泛的应用。
从几何角度来看,积分运算就是求出函数Y = f (t )曲线与横轴所围成的面积,从t =t 0到t n 时刻,函数Y= f (t )的积分值可表述为⎰⎰==n n tt t t dt )t (Ydt S 00f如果进一步将t ∈[t 0,t n ]的时间区划分为若干个等间隔Δt 的小区间,当Δt 足够小时,函数Y 的积分可用下式近似表示t Y Ydt S n i i tt n ∆∑⎰-=≈=1在几何上就是用一系列的小矩形面积之和来近似表示函数f (t )以下的积分面积。
专利名称:一种采用时间参数多项式插补的自由曲面数控加工方法
专利类型:发明专利
发明人:卢磊,韩江,夏链,董方方,刘海军
申请号:CN201810049584.X
申请日:20180118
公开号:CN108227630A
公开日:
20180629
专利内容由知识产权出版社提供
摘要:本发明涉及一种采用时间参数多项式插补的自由曲面数控加工方法。
具体包括三大步骤:预测前瞻速度规划、以B‑spline为基础的时间参数多项式加工轨迹生成和时间参数多项式实时插补;
(1)通过读取参数曲线型自由曲面加工轨迹进行速度规划,生成高速高精的自由曲面加工过程离散数据;2)采用给定精度的B‑spline拟合技术对经速度规划后的高速高精加工过程离散数据进行表征,然后转换成简洁增量式时间参数多项式曲面加工轨迹;(3)根据生成的时间参数多项式曲面加工轨迹编制相应实时插补程序对数控机床进行实时控制,完成自由曲面加工。
本发明改善了所加工出的自由曲面的轮廓精度与表面质量,显著提高了自由曲面加工效率,减少了自由曲面加工所需数据量。
申请人:合肥工业大学
地址:230009 安徽省合肥市包河区屯溪路193号
国籍:CN
代理机构:合肥金安专利事务所
代理人:金惠贞
更多信息请下载全文后查看。
渐开线插补的时间分割法
熊俊良
【期刊名称】《兵工自动化》
【年(卷),期】2006(025)001
【摘要】渐开线插补的时间分割法采用若干等弦逼近实际的渐开线。
通过插补运算计算出每个插补周期内X、Y轴的进给量控制相应轴的运动,且两插补点间距离相等以保证等线速进给。
该运算可获得较高的插补精度和插补速度。
【总页数】1页(P15)
【作者】熊俊良
【作者单位】中国兵器工业第58研究所数控部,四川绵阳621000
【正文语种】中文
【中图分类】TG659
【相关文献】
1.时间分割法的渐开线插补 [J], 刘华建
2.时间分割法圆弧插补的改进 [J], 向平
3.基于时间分割法的圆渐开线涡旋压缩机涡旋齿插补研究 [J], 黄小华; 王训杰
4.基于时间分割法的圆渐开线涡旋压缩机涡旋齿插补研究 [J], 黄小华; 王训杰
5.一种基于时间分割法和数字积分法混合实现的空间直线插补方法 [J], 刘宜;丛爽;钱炜;方凯
因版权原因,仅展示原文概要,查看原文内容请购买。