第三节 数据采样法插补

数据清洗与整理中的缺失值填补与插值技术解析在数据分析的过程中，缺失值是一个常见的问题。

缺失值的存在可能会导致结果的不准确性和误导性，因此需要采取相应的处理措施。

本文将对数据清洗与整理中的缺失值填补与插值技术进行解析。

一、缺失值的种类和原因缺失值是指数据集中的某些观测值或变量值缺失的情况。

它可以分为完全缺失和部分缺失两种情况。

完全缺失是指某一观测值的所有变量都缺失，通常是由于人为原因或者数据采集过程中的错误导致的。

部分缺失是指某个变量在一部分样本中缺失，可能是由于无法获得该变量的观测值或者观测值不可靠导致的。

导致缺失值的原因多种多样，包括实验设备故障、调查问卷的遗漏、受访者的拒绝回答等。

在现实的数据分析过程中，我们需要面对各种各样的数据集，其中缺失值是无法避免的。

因此，我们需要掌握填补和插值技术来处理这些缺失值。

二、缺失值的处理方法1. 删除法删除法是最简单粗暴的处理方法，即将缺失值所在的观测样本或变量删除。

如果缺失值非常少，对整体数据影响较小，可以选择删除该样本；如果缺失值相对较多，或者缺失的是关键变量，删除该样本可能会带来信息的丢失，甚至可能导致结果的失真。

因此，在实际应用中，删除法并不是一种常见的处理缺失值的方法。

2. 均值、中位数或众数填补在某些情况下，可以通过使用其他观测样本或变量的均值、中位数或众数来填补缺失值。

这种方法简单快捷，适用于连续型和离散型变量。

然而，该方法的局限性在于无法考虑其他变量之间的关系，可能会引入一定的误差。

3. 回归分析法填补回归分析法是一种比较常用的缺失值填补方法。

它通过建立与缺失变量有关的回归模型，利用其他完整的变量对缺失变量进行预测。

这种方法可以充分利用已有数据的信息，增加填补后的准确性。

但是，回归分析法的前提是已有数据具有一定的线性关系，否则可能带来一定的误差。

4. 插值法插值法是一种通过利用现有数据的空间和时间特性来估计缺失值的方法。

常见的插值方法有线性插值、多项式插值、样条插值等。

国家精品资源共享课新增习题及答案第3章 数控系统控制原理1.在数控采样插补中插补周期与插补运算时间有什么关系？插补周期与插补运算时间有密切的关系，一旦选定了插补算法，完成插补运算的最大指令条数也就确定了，则此算法占用计算机CPU的时间也就确定了。

一般来说，插补周期T必须大于插补运算时间，因为在一个插补周期内，计算机除了要完成插补运算外，还要执行显示、监控甚至精插补等任务，插补周期等于插补运算时间与完成其它任务所占用的时间之和。

另外，插补周期还会对圆弧的插补误差产生一定的影响。

2.试分析在弦线逼近圆弧数据采样插补中， 逼近误差与速度、插补周期和圆弧半径的关系。

答：对于圆弧插补，动点在一个插补周期运动的直线段以弦线逼近圆弧时，逼近误差与速度、插补周期的平方成正比，与圆弧半径成反比，即2()18rTVer =，T-插补周期，V-刀具移动速度，r-圆弧半径，e r-逼近误差。

在一台数控机床上，允许的插补误差是一定的，它应小于数控机床的分辨率，即应小于一个脉冲当量。

那么，较小的插补周期，可以在小半径圆弧插补时允许较大的进给速度。

从另一角度讲，在进给速度、圆弧半径一定的条件下，插补周期越短，逼近误差就越小但插补周期的选择要受计算机运算速度的限制。

首先，插补计算比较复杂,需要较长时间。

此外，计算机除执行插补计算之外，还必须实时地完成其它工作，如显示、监控、位置采样及控制等。

所以，插补周期应大于插补运算时间与完成其它实时任务所需时间之和。

3.在数据采样插补中，粗插补和精插补一般怎样实现？答：粗插补，一般用软件实现；精插补，一般用硬件实现。

在每一插补周期中，调用一次插补程序，用软件粗插补计算出各坐标轴在下一插补周期内的位移增量（而不是单个脉冲），然后送到硬件插补器内，经过硬件插补器精插补后，再控制电机驱动运动部件达到相应的位置。

4.试述刀具半径补偿的过程。

答：刀具半径补偿过程分为以下三个步骤:(1)刀具半径补偿的建立；(2)刀具半径补偿进行；(3)刀具半径补偿注销（G40）。

将对应的位置增量数据(如、)，再与采样所获得的实际位置反馈值 相比较，求得位置跟踪误差。位置伺服软件就根据当前的位置误差 计算出进给坐标轴的速度给定值，并将其输送给驱动装置，通过电 动机带动丝杠和工作台朝着减少误差的方向运动，以保证整个系统 的加工精度。由于这类算法的插补结果不再是单个脉冲，而是一个 数字量，所以，这类插补算法适用于以直流或交流伺服电动机作为 执行元件的闭环或半闭环数控系统中。
对圆弧，提供起点、终点、顺圆或逆圆、以及圆心相对于起点的位置。为满
足零件几何尺寸精度要求，必须在刀具(或工件)运动过程中实时计算出满足 线形和进给速度要求的若干中间点(在起点和终点之间)，这就是数控技术中
插补(Interpolation)的概念。据此可知，插补就是根据给定进给速度和给定
轮廓线形的要求，在轮廓已知点之间，确定一些中间点的方法，这种方法称 为插补方法或插补原理。
Xm+1＝Xm+1, Ym+1＝Ym
新的偏差为
Fm+1＝Ym+1Xe－Xm+1Ye＝Fm－Ye
若Fm＜0时，为了逼近给定轨迹，应向＋Y方向进给一步，走一步后新的坐标值为
Xm+1＝Xm, Ym+1＝Ym ＋1
新的偏差为
Fm+1＝Fm＋Xe
4. 终点判别法
逐点比较法的终点判断有多种方法，下面主要介绍两种：
直到∑为零时，就到了终点。
2.2
不同象限的直线插补计算
上面讨论的为第一象限的直线插补计算方法，其它三个象
限的直线插补计算法，可以用相同的原理获得，表5-1列出了
四个象限的直线插补时的偏差计算公式和进给脉冲方向，计 算时，公式中Xe，Ye均用绝对值。
表1-1 四个象限的直线插补计算

Y积分器
计t数 器JVX为(XeJ)E，JR均X 为溢三出位Jvy(Ye) JRy 溢出
终点计 数器
JE
备注
二0进制1存01 放器00。0
011 000
000
初始状态
1
101 101
011 011
001 第一次迭代
2
101 010
1
011 110
010
X溢出
3
101 111
011 001
1
011
Y溢出
∑=8-1=7
4
F<0
+Y
F4=F3+xe=-2+6=4
∑=7-1=6
5
F>0
+X
F5=F4-ye=4-4=0
∑=6-1=5
6
F=0
+X
F6=F5-ye=0-4=-4
∑=5-1=4
7
F<0
+Y
F7=F6+xe=-4+6=2
∑=4-1=3
8
F>0
+X
F8=F7-ye=2-4=-2
∑=3-1=2
9
F<0
4
101 100
1
011 100
100
X溢出
5
101 001
1
011 111
101
X溢出
6
101 110
011 010
1
110
Y溢出
7
101 011
1
011 101
111
件加工的要求，现在的数控系统已很少采用这类算法 了。
4
*

解：插补完这段直线刀具沿Ｘ和Ｙ轴应走的总步数为 = x e + y e ＝5 + 3＝8。 Y 刀具的运动轨迹如图 E(5，3) 3
2 1 O 1 2 3 4 5 X
第二节 基准脉冲插补
插补运算过程见表：
循环序号 偏差判别 F ≥0 坐标进给 +X 偏差计算 Fi+1=Fi-ye
教案 3
终点判别
m
Y
m(Xm,Ym) B(XB,YB)
+Y2
2 m-R
若Fm=0，表示动点在圆弧上；
若Fm>0，表示动点在圆弧外； 若Fm<0，表示动点在圆弧内。
Rm
R A(XA,YA)
第Ⅰ象限逆圆弧
X
第二节 基准脉冲插补
2）坐标进给
教案 3
与直线插补同理，坐标进给应使加工点逼近给定圆弧,规定如下： 当Fm≥0时，向-X方向进给一步； 当Fm＜0时，向+Y方向进给一步。
教案 3
若Fi=0，表示动点在直线OE上，如P； 若Fi>0，表示动点在直线OE上方，如P′； 若Fi<0，表示动点在直线OE下方，如P″。
O
xi 第Ι象限直线
X
第二节 基准脉冲插补
2）坐标进给
教案 3
坐标进给应逼近给定直线方向，使偏差缩小的方向进给一步，由插补装 置发出一个进给脉冲控制向某一方向进给。
教案 3
直线线型 进给方向 偏差计算 直线线型
L1、L4 L2、L3 +X -X Fi+1=Fi-ye L1、L2 L3、L4
偏差计算
Fi+1=Fi+xe
注：表中L1、L2、L3、L4分别表示第Ⅰ、第Ⅱ、 第Ⅲ、第Ⅳ象限直线，偏差计算式中xe、ye均代 入坐标绝对值。

3. C刀具半径补偿方法
B刀具半径补偿只根据本程序段进行刀具半径 补偿计算，不能很好解决程序段轨迹之间的 过渡问题。
C刀具补偿技术的关键在于如何实现组成零 件轮廓的各轨迹间拐角的过渡。它的计算是 根据零件尺寸和刀具半径计算出刀具中心轨 迹，求出前后两条刀具中心轨迹的交点或过 渡轨迹。
（1）C刀补设计思想
偿一个相反的刀补，称为取消 刀补。
二 . 刀具半径补偿
1）刀具半径补偿的作用
轮廓铣削中，由于刀具总有一定半径，刀具 中心的运动轨迹与零件轮廓不一致，因此数 控系统需要进行刀具中心轨迹计算，使刀具 沿零件轮廓自动偏移一个半径值，这一功能 就是刀具半径补偿功能。（如图示）
2） B刀具半径补偿
B刀补缺陷的原因；单 段读、单段算、单段走
C刀补要考虑下一段加 工轨迹的影响，就要设
四个寄存器：工作寄存 器存放在加工的程序段 信息；刀补寄存器存放 下一段要加工的；缓冲 寄存器存放下一段要加 工的信息。要执行的结 果存入输出寄存器。
（2） 自动过渡转接方式
C刀补偿的主要特点就是采用直线过渡。 不同的转接类型： 直线到直线、直线到圆弧、圆弧到圆弧，
3）插补周期与速度、精度的关系。

e展R开=R并（略1去-c高on阶δ 项/2，）注，意c到onΔδL=/T2F
用幂级数 δ=Δ L/R
可以eR=δ 2 R/8= （TF）2 /8R 由此可以确定插补周期T。
§4-5 刀具补偿
当采用不同尺寸的刀具加工同一轮廓工件 同一名义尺寸的刀具因磨损、换刀而引起尺
（3）C刀补过切削的判别
（4）C刀补的执行过程
C刀补的执行过程分成三步： 刀补建立； 刀补执行； 刀补撤销

第四节数据采样法随着数控系统中计算机的引入，大大缓解了插补运算时间和计算复杂性之间的矛盾，特别是高性能直流伺服系统和交流伺服系统的研制成功，为提高现代数控系统的综合性能创造了充分条件。

相应地，这些现代数控系统中采用的插补方法，就不再是最初硬件数控系统中所使用的脉冲增量法，而是结合了计算机采样思想的数据采样法。

所谓数据采样法就是利用一系列首尾相连的微小直线段来逼近给定曲线。

由于这些线段是按加工时间来分割的，因此，数据采样法又称为“时间分割法”。

一般来讲，分割后所得到的微小直线段相对系统精度而言仍显过大，需要在微小直线段的基础上进一步密化数据点。

获取微小直线段的过程称为粗插补，将微小直线段进一步密化的过程称为精插补。

通过两者的紧密配合即可实现高性能零件轮廓插补。

一般情况下，数据采样插补法中的粗插补是由软件实现。

由于粗插补可能涉及到一些比较复杂的函数运算，因此，大多采用高级语言完成。

而精插补算法大多采用前面介绍的脉冲增量法，它既可由软件实现也可由硬件实现，由于相应算术运算较简单，所以软件实现时大多采用汇编语言完成。

一、插补周期与位置控制周期所谓插补周期T S是指相邻两个微小直线段之间的插补时间间隔，而位置控制周期T C则是数控系统中伺服位置环的采样控制时间间隔。

对于给定的数控系统而言，插补周期和位置控制周期是两个固定不变的时间参数。

通常取T S≥T C，目的是便于系统内部控制软件的处理。

当T S与T C不相等时，一般要求T S是T C的整数倍。

这是由于插补运算较复杂，处理时间较长；而位置环数字控制算法较简单，处理时间较短。

因此，每次插补运算的结果可供位置环多次使用。

现假设程编进给速度为F，插补周期为T S，则可求得插补分割后的微小直线段长度为∆L（暂不考虑单位）为∆L=FT S。

插补周期T S对系统稳定性没有影响，但对被加工轮廓的轨迹误差有影响。

位置控制周期T C不仅对系统稳定性而且对轮廓误差均有影响。

xi +1 = xi + 1 yi +1 = yi Fi +1 = xe y i −( xi + 1) ye = ( xe yi − xi ye ) − ye
于是有 Fi+1 = Fi －Ye
E(xe,ye) Pi(Xi,Yi) Pi+1(Xi+1,Yi+1)
0
x
第三章轮廓加工的数学基础
为了逼近曲线的相对位置沿 2）.若Fi<0为了逼近曲线的相对位置沿+y向走 为了逼近曲线的相对位置 一步即 y
y E(xe,ye)
0
x
设动点pi ( xi , yi )的Fi 值为
为便于计算机编程计算, 为便于计算机编程计算,
Fi = xe yi − xi ye
y
的计算予以简化。 将F的计算予以简化。 的计算予以简化 为了逼近曲线的相对位置沿 向走一步 向走一步， 1）.若Fi>0为了逼近曲线的相对位置沿+x向走一步，即 为了逼近曲线的相对位置
第三章轮廓加工的数学基础
3.1.1直线插补原理 3.1.1直线插补原理 1.偏差函数 1.偏差函数
如图所示， 如图所示，设规定轨迹为 直线段OE，起点在原点，终 起点在原点， 点E的坐标A(XeYe) , Pi(xi, yi)为加工点 。
Y
E ( Xe,Ye)
Pi(xi,yi) 0 x
则下式成立。 （1）.若P正好处在 OE 上,则下式成立。
3
F<0 ∆Y F=F+5 5
F计算 计算 -3 终点判别(n-1→n) → 终点判别 7 ≠0 6 ≠0 5 ≠0 4 ≠0 3 ≠0
0
Pi(xi,yi)

3.逐点比较法圆弧插补 3.逐点比较法圆弧插补
（1）偏差函数 任意加工点P ），偏差函数 偏差函数F 任意加工点Pi（Xi，Yi），偏差函数Fi可表示为
Fi = X i2 + Yi 2 − R 2
=0，表示加工点位于圆上； 若Fi=0，表示加工点位于圆上； Y >0，表示加工点位于圆外； 若Fi>0，表示加工点位于圆外； <0， 若Fi<0，表示加工点位于圆内
Y Ae (Xe,Ye) F>0 Pi (Xi,Yi) F<0 X
为便于计算机计算) （2）偏差函数字的递推计算 (为便于计算机计算 为便于计算机计算 >=0，规定向+ 方向走一步（若坐标单位用脉冲当量表示） 若Fi>=0，规定向+X方向走一步（若坐标单位用脉冲当量表示）
Xi+1 = Xi +1 Fi+1 = XeYi −Ye (Xi +1) = Fi −Ye
2.逐点比较法直线插补 2.逐点比较法直线插补
（1）偏差函数构造 对于第一象限直线OA上任一点( OA上任一点 对于第一象限直线OA上任一点(X,Y) YX e − XYe = 0 若刀具加工点为Pi（ ），则该点的偏差 若刀具加工点为Pi（Xi，Yi），则该点的偏差 Pi 函数F 函数Fi可表示为 Fi = Yi X e − X i Ye 若Fi=0，表示加工点位于直线上； 表示加工点位于直线上； 表示加工点位于直线上方； 若Fi>0，表示加工点位于直线上方； 表示加工点位于直线下方。 若Fi<0，表示加工点位于直线下方。
F=0 F<0 F>0 F<0 F>0 F=0 F<0 F>0 F<0 F>0

Xi|、坐标|Yi|、总步数Σ＝＋|Ye－Ys|在内存中均占用三个字节，
并且F采用补码形式，其余数据采用绝对值或正数，地址分配 情况如表3-6所示。
14603C
表3-6 第Ⅰ象限逆圆插补参数地址分配表
14603C
(三)插补实例
例3-4设将要加工的零件轮廓为第Ⅰ象限逆圆，如图3-9所示， 圆心在坐标原点，起点为S(4，3)，终点为E(0，5)，试用逐点比
4。该圆弧插补运算过程如表3-11所示，插补轨迹如图3-25的折
线所示。
14603C
表3-11 DDA圆弧插补运算过程
14603C
四、数字积分法插补的象限处理
表3-12 DDA法插补不同象限直线和圆弧情况
14603C
五、提高数字积分法插补质量的措施
(一)合成进给速度 (二)进给速度均匀化的措施
14603C
(三)插补实例
例3-6设有第Ⅰ象限逆圆弧，如图3-25所示，起点为S(4，0)，终 点为E(0，4)，且寄存器位数N=3。试用DDA法对该圆弧进行插
补，并画出插补轨迹。
解 插补开始时，被积函数寄存器初值分别为 JVX＝Ys＝0，J
VY＝Xs＝4，终点判别寄存器JΣX＝|Xe－Xs|＝4，JΣY＝|Ye－Ys|＝
图3-17 合成进给速度 与轴速度的关系
14603C
四、逐点比较法合成进给速度
图3-18 合成进给速度变化曲线
14603C
第三节 数字积分法 一、数字积分法基本原理 二、数字积分法直线插补
三、数字积分法圆弧插补
四、数字积分法插补的象限处理 五、提高数字积分法插补质量的措施
14603C
一、数字积分法基本原理
→NR2→NR3→NR4→NR1→…；顺圆过象限的转换顺序是：SR1→

E（Xe，Ye）
N（Xi，Yi） X
Yi Ye Xi Xe
使用一个正数XeXi乘以该式，最后得
Fi X eYi X iYe
（3-1）
很显然，偏差值Fi的符号反映了动点N相对于直线OE的位置偏离情况。 ① Fi = 0 时，动点N在直线上； ② Fi ≻ 0 时，动点N在直线的上方区域； ③ Fi ≺ 0 时，动点N在直线的下方区域。
② 直线和圆弧是构成零件轮廓的基本线型，所以绝大多数数控系统都 具有直线插补和圆弧插补功能。 本课程将重点介绍直线插补和圆弧插补的计算方法。
③ 插补运算速度是影响刀具进给速度的重要因素。为减少插补运算时 间，在插补运算过程中，应该尽量避免三角函数、乘、除以及开方等复杂运 算。因此插补运算一般都采用迭代算法。 ④ 插补运算速度直接影响数控系统的运行速度；插补运算精度又直接 影响数控系统的运行精度。 插补速度和插补精度之间是相互制约、互相矛盾的，因此只能折中选择。
a0 a1 a2 a3 a4 a5 a6 a7 a0 a1 a2 a3 a4 a5 a6 a7 a8 a9
(a)
(b)
所谓插补，就是根据零件轮廓的几何形状、几何尺寸以及轮廓加工的 精度要求和工艺要求，在零件轮廓的起点和终点之间插入一系列中间点 （折线端点）的过程，即所谓“数据点的密化过程”，其对应的算法称为 插补算法。
刀具进给 逐点比较法刀具进给方向的选择原则： ① 平行于某个坐标轴； ② 减小动点相对于零件轮廓的位置偏差。 根据这个原则可以判断出直线插补的刀具进给方向为： ① 当动点在直线上方区域时， 应 +X 方向进给一步； ② 当动点在直线下方区域时，应 +Y 方向进给一步； ③ 动点在直线上时， 既可以+X方向也可以+Y方向进给一步，在此约定 取+X方向。

数据插补的方法概述数据插补是指通过利用已有数据的特征和规律，对缺失或者不完整的数据进行估算和修补的过程。

在实际的数据分析和机器学习任务中，由于各种原因，数据中可能存在缺失值，这些缺失值会影响到后续的分析和建模过程。

因此，数据插补的方法至关重要。

缺失值的类型缺失值可以分为完全缺失和部分缺失两种类型。

完全缺失表示某个样本的某个特征完全缺失，而部分缺失表示某个样本的某个特征部分缺失。

缺失值的影响缺失值会对数据分析和建模带来很大的干扰，主要体现在以下几个方面： 1. 数据分布的偏移：缺失值可能导致数据的分布不再符合原来的特征。

2. 统计量的变化：缺失值会影响统计量的计算，进而影响数据的分析结果。

3. 建模效果下降：缺失值会导致训练样本减少，从而降低建模的准确性和鲁棒性。

常用的数据插补方法在实际应用中，有多种方法可以进行数据插补。

下面我们将介绍几种常用的数据插补方法。

1. 均值插补均值插补是指通过计算已有数据的均值，将缺失值替换为该均值。

这种方法适用于缺失值较少且缺失值处于特征数据的中心位置的情况。

2. 中位数插补中位数插补类似于均值插补，只不过是将缺失值替换为已有数据的中位数。

中位数插补对异常值比较敏感，适用于数据分布存在偏斜的情况。

3. 最近邻插补最近邻插补是指通过寻找与缺失样本特征最相似的样本，将其特征值进行插补。

这种方法适用于缺失值在特征空间中有一定的局部结构的情况。

4. 回归插补回归插补是指通过建立缺失特征与其他特征之间的回归关系，利用已有数据进行插补。

回归插补适用于缺失数据与其他特征之间存在较强相关性的情况。

插补方法选择的考虑因素在选择合适的插补方法时，需要考虑多个因素： 1. 缺失数据的类型：不同类型的缺失数据需要应用不同的插补方法。

2. 数据的分布特征：数据的分布特征会影响插补方法的选择。

3. 缺失数据的数量：缺失数据的数量多少也会对插补方法的选择产生影响。

4. 预测精度要求：不同的插补方法具有不同的预测精度，需要根据具体需求选择合适的方法。

2013-8-13 9
一.逐点比较法直线插补算法
⑴判别函数及判别条件 如图所示，对XY平面第一象限直线段进 行插补。直线段起点位于坐标原点O，终点位 于A（Xe,Ye）。设点P（Xi，Yi）为任一动点。 若P点在直线OA上，则： Y XeYi – XiYe = 0 A (X Y ） 若P点在直线OA上方，则： F＞0 P (X Y ） XeYi – XiYe > 0 若P点在直线OA下方，则： F＜0 XeYi – XiYe < 0 X
2013-8-13
Y E(Xe,Ye) ) O X
15
四个象限直线的偏差符号和插补进给方向如下图所示， 用L1、L2、L3、L4分别表示第Ⅰ、Ⅱ、Ⅲ、Ⅳ象限的直线。 为适用于四个象限直线插补，插补运算时用∣X∣， ∣Y∣代替X，Y，偏差符号确定可将其转化到第一象限， 动点与直线的位置关系按第一象限判别方式进行判别。
2013-8-13
4
脉冲增量插补法比较适用于步进电机作 为驱动电机的系统。有下列常见的几种：
（ 1 ）数字脉冲乘法器 （ 2 ）逐点比较方法 （ 3 ）数字积分方法 （ 4 ）比较积分方法 （5）最小偏差方法 （ 6 ）直接函数方法
2013-8-13
5
（二）数字增量（数据采样）插补算法
1.数字增量插补的特点 数字增量插补也称数据采样插补，它为时间标量插 补，这类插补算法的特点是插补运算分两步完成：第 一步是粗插补：计算出插补周期内各坐标轴的增量值。 第二步是精插补：根据采样得到的实际位置增量值， 计算跟随误差，得到速度指令，输出给伺服系统，通 常称为精插补。这种方法比较适用于伺服电机作为驱 动电机的系统 ⑴粗插补 它是在给定起点和终点的曲线之间插入若干个点， 即用若干条微小直线段来逼近给定的曲线，这些微小 直线段的长度ΔL相等且与给定的进给速度有关。由于 粗插补在每个插补周期内之计算一次，因此每一微小 直线段的长度ΔL与进给速度F和插补周期T的关系如下： ΔL=FT。粗插补在每个插补周期内计算出坐标位置增 量值。

刀尖位置与机床控制刀位点不同时，需要刀尖位置 补偿。刀具磨损或者换了新的刀具后，实际刀尖位置变 化，需要补偿。
14
3.6 刀具半径补偿 数 控 技 术
第 三 章
1）B功能刀具半径补偿计算： ◆直线加工时刀具补偿；
Y
A(x,y) ∆y r A’(x’,y’)
第 三 章
计 算 机 数 控 装 置
扩展DDA插补是在DDA插补的基础上发展起来，并将DDA法 用切线逼近圆弧的方法改进为用割线逼近，减少了逼近误差， 提高了圆弧插补的精度。
7
3.5 数据采样插补的原理 数 一. 数据采样插补的基本思想 控 (二) 数据采样法之二——扩展DDA法 技 1 .扩展DDA直线插补 V 术 X V T TX X
第 三 章
ΔPAG∽ΔAOC
AOC PAC i
i 1 i
1 i 2
计 算 机 数 控 装 置
插补步长和角步距的关系
l cos X
l sin Y
5
3.5 数据采样插补的原理
数 一. 数据采样插补的基本思想 控 直线函数法的主要问题： 技 1.用弦线逼近圆弧，因此插补误差主要为半径的绝对误差。 术 因插补周期是固定的，该误差取决于进给速度和圆弧半径，
第 三 章
直线与X轴夹角为，若已知轮廓步长，则本次插补周期内各坐 标轴进给量为： X l cos
计 算 机 数 控 装 置
Ye Y x Xe
下式可以避免计算三角函数：
cos
Xe X e2 Ye2一. 数据采样插补的基本思想 控 2. 直线函数法圆弧插补： 技 直线函数法圆弧插补，需先根据进给速度指令F，计算出 术 轮廓步长l，然后以长为l的弦线逼近圆弧，再将弦l分解到两个

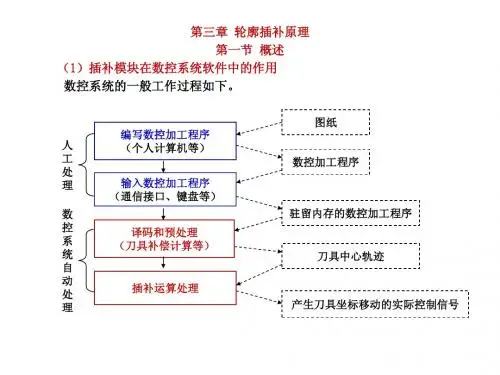
什么是插补一、插补的概念在数控机床中，刀具不能严格地按照要求加工的曲线运动，只能用折线轨迹逼近所要加工的曲线。

插补（interpolation）定义：机床数控系统依照一定方法确定刀具运动轨迹的过程。

也可以说，已知曲线上的某些数据，按照某种算法计算已知点之间的中间点的方法，也称为“数据点的密化”。

数控装置向各坐标提供相互协调的进给脉冲，伺服系统根据进给脉冲驱动机床各坐标轴运动。

数控装置的关键问题：根据控制指令和数据进行脉冲数目分配的运算（即插补计算），产生机床各坐标的进给脉冲。

插补计算就是数控装置根据输入的基本数据，通过计算，把工件轮廓的形状描述出来，边计算边根据计算结果向各坐标发出进给脉冲，对应每个脉冲，机床在响应的坐标方向上移动一个脉冲当量的距离，从而将工件加工出所需要轮廓的形状。

插补的实质：在一个线段的起点和终点之间进行数据点的密化。

插补工作可由硬件逻辑电路或执行软件程序来完成，在CNC系统中，插补工作一般由软件完成，软件插补结构简单、灵活易变、可靠性好。

二、插补方法的分类目前普遍应用的两类插补方法为基准脉冲插补和数据采样插补。

1.基准脉冲插补（行程标量插补或脉冲增量插补）特点：每次插补结束，数控装置向每个运动坐标输出基准脉冲序列，每插补运算一次，最多给每一轴一个进给脉冲。

每个脉冲代表了最小位移，脉冲序列的频率代表了坐标运动速度，而脉冲的数量表示移动量。

每发出一个脉冲，工作台移动一个基本长度单位，也叫脉冲当量，脉冲当量是脉冲分配的基本单位。

该方法仅适用于一些中等精度或中等速度要求的计算机数控系统主要的脉冲增量插补方法：数字脉冲乘法器插补法逐点比较法数字积分法矢量判别法比较积分法最小偏差法目标点跟踪法单步追踪法直接函数法加密判别和双判别插补法2. 数字采样插补（数据增量插补）数据采样插补又称时间增量插补，这类算法插补结果输出的不是脉冲，而是标准二进制数。

根据程编进给速度，把轮廓曲线按插补周期将其分割为一系列微小直线段，然后将这些微小直线段对应的位置增量数据进行输出，以控制伺服系统实现坐标轴的进给。

2
2
(TF) 2 eR R 8 8R
– 由上式可以看出，圆弧插补时，插补周期T分 别与误差eR、圆弧半径R和进给速度F有关。在 给定圆弧半径和弦线误差极限的情况下，插补 周期短对获得高的加工速度有利。在插补周期 确定的情况下，加工给定半径的圆弧时，为了 保证加工精度，必须对加工速度进行限制。
以第一象限顺圆圆m
1 i 2
1 Yi Yi 1 2 cos cos i 2 R -
1 2
1 Yi Yi -1 2 cos R
X i f cos
数据采样插补原理
数据采样插补法又称数字增量插补法或时间标量 插补法，用在闭环、半闭环交直流伺服电机驱动 的控制系统中，插补结果输出的不是脉冲，而是 数据。计算机定时地对反馈回路采样，得到采样 数据与插补程序所产生的指令数据相比较后，以 误差信号输出，驱动伺服电动机。 数据采样插补可以划分两个阶段：粗插补和精插 补，其中粗插补是主要环节。粗插补是用微小的 直线段逼近给定的轮廓，该微小的直线段与指令 给定的速度有关，常用软件实现；精插补是在上 述微小的直线段上进行“数据点的密化”，这一 阶段其实就是对直线的脉冲增量插补，计算简单， 可以用硬件或软件实现。这种插补方法所产生的 最大速度不受计算机最大运算速度的限制，但插 补程序比较复杂。
– 数据采样插补的最大进给速度不受计算机最大运算速 度的限制，而主要受圆弧弦线误差和伺服系统性能的 限制。 – 在直线插补中，插补形成的每个微小线段与给定的直 线重和，不会造成轨迹误差。但在圆弧插补中，通常 用内接弦线或内、外均差弦线来逼近圆弧，这种逼近 必然要造成轨迹误差。
(TF) eR R 8 8R
2

F>0?
Y 沿-x向走一步
Fi +1, j = Fi , j + 2 xi + 1
沿y向走一步
F ← F − | xe |
n=n-1 n=0?
Y 结束 N
n=n-1 n=0?
Y 结束 N
10
4.逐点比较法的速度分析
L N = V f
式中：L —直线长度； V —刀具进给速度； N —插补循环数； f —插补脉冲的频率。
F=0 F<0 F>0 F<0 F>0 F=0 F<0 F>0 F<0 F>0
+X +Y +X +Y +X +X +Y +X +Y +X
F1=F0-ye=0-4=-4 F2=F1+xe=-4=6=2 F3=F2-ye=2-4=-2 F4=F3+xe=-2+6=4 F5=F4-ye=4-4=0 F6=F5-ye=0-4=-4 F7=F6+xe=-4+6=2 F8=F7-ye=2-4=-2 F9=F8+xe=-2+6=4 F =F -y =4-4=0
3
2.逐点比较法直线插补
（1）偏差函数构造 对于第一象限直线OA上任一点(X,Y)
YX e − XYe = 0
若刀具加工点为Pi（Xi，Yi），则该点的偏差 函数Fi可表示为 Fi = Yi X e − X i Ye 若Fi=0，表示加工点位于直线上； 若Fi>0，表示加工点位于直线上方； 若Fi<0，表示加工点位于直线下方。
逆圆
（2）坐标变换法 用第一象限逆圆插补的偏差函数进行第三象限逆圆和第二、 四象限顺圆插补的偏差计算，用第一象限顺圆插补的偏差函 数进行第三象限顺圆和第二、四象限逆圆插补的偏差计算。