第60次作业八一班数学作业本2015年春季学期钟南附中作业存放 Microsoft Word 文档

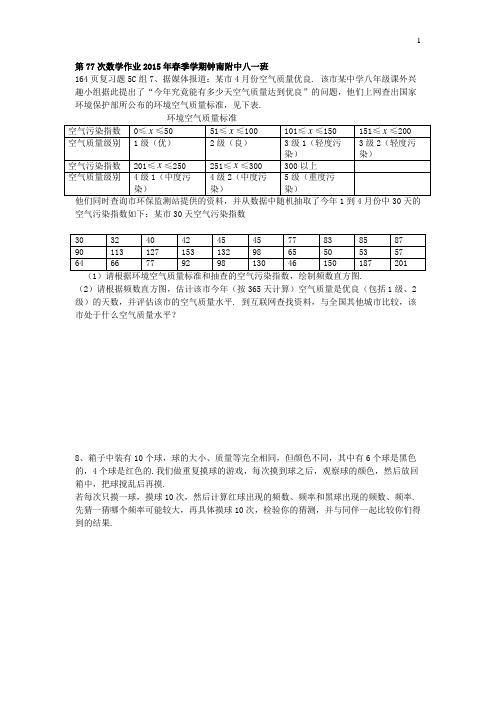
1第77次数学作业2015年春季学期钟南附中八一班164页复习题5C组7、据媒体报道：某市4月份空气质量优良. 该市某中学八年级课外兴趣小组据此提出了“今年究竟能有多少天空气质量达到优良”的问题，他们上网查出国家环境保护部所公布的环境空气质量标准，见下表.环境空气质量标准空气污染指数0≤x≤50 51≤x≤100 101≤x≤150 151≤x≤200空气质量级别1级（优）2级（良）3级1（轻度污染）3级2（轻度污染）空气污染指数201≤x≤250 251≤x≤300 300以上空气质量级别4级1（中度污染）4级2（中度污染）5级（重度污染）他们同时查询市环保监测站提供的资料，并从数据中随机抽取了今年1到4月份中30天的空气污染指数如下：某市30天空气污染指数30 32 40 42 45 45 77 83 85 8790 113 127 153 132 98 65 50 53 5764 66 77 92 98 130 46 150 187 201 （1）请根据环境空气质量标准和抽查的空气污染指数，绘制频数直方图.（2）请根据频数直方图，估计该市今年（按365天计算）空气质量是优良（包括1级、2级）的天数，并评估该市的空气质量水平. 到互联网查找资料，与全国其他城市比较，该市处于什么空气质量水平？8、箱子中装有10个球，球的大小、质量等完全相同，但颜色不同，其中有6个球是黑色的，4个球是红色的.我们做重复摸球的游戏，每次摸到球之后，观察球的颜色，然后放回箱中，把球搅乱后再摸.若每次只摸一球，摸球10次，然后计算红球出现的频数、频率和黑球出现的频数、频率.先猜一猜哪个频率可能较大，再具体摸球10次，检验你的猜测，并与同伴一起比较你们得到的结果.。

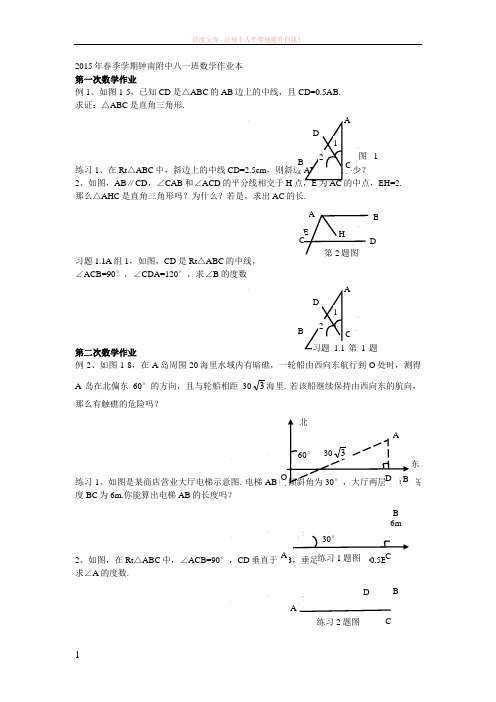
2015年春季学期钟南附中八一班数学作业本第一次数学作业例1、如图1-5，已知CD 是△ABC 的AB 边上的中线，且CD=0.5AB.求证：△ABC 是直角三角形.练习1、在Rt △ABC 中，斜边上的中线CD=2.5cm ，则斜边AB 的长是多少？2、如图，AB ∥CD ，∠CAB 和∠ACD 的平分线相交于H 点，E 为AC 的中点，EH=2. 那么△AHC 是直角三角形吗？为什么？若是，求出AC 的长.习题1.1A 组1，如图，CD 是Rt △ABC 的中线，∠ACB=90°，∠CDA=120°，求∠B 的度数第二次数学作业例2、如图1-8，在A 岛周围20海里水域内有暗礁，一轮船由西向东航行到O 处时，测得A 岛在北偏东60°的方向，且与轮船相距303海里. 若该船继续保持由西向东的航向，那么有触礁的危险吗？练习1、如图是某商店营业大厅电梯示意图. 电梯AB 的倾斜角为30°，大厅两层之间的高度BC 为6m.你能算出电梯AB 的长度吗？2、如图，在Rt △ABC 中，∠ACB=90°，CD 垂直于AB ，垂足为点D ，DB=0.5BC ， 求∠A 的度数.1 2 AB C D图1-H E A B C D 第2题图 1 2 AB C D习题1.1第1题60° O 北 东 A B D 303 30° A 练习1题图 B 6m C A 练习2题图B C D习题1.1A 组2、如图，在△ABC 中，已知∠B=21∠A=31∠C ，AB=8cm. （1）求证：△ABC 为直角三角形；（2）求AB 边上的中线长.第三次数学作业习题1.1A 组3题如图，线段AE 与BC 相交于点D ，BD=CD ，AD=ED ，CA ⊥AE ， ∠1=30°，且AB=3cm. 那么线段BE 多长呢？4、如图，在Rt △ABC 中，∠ACB=90°，∠B=30°，高，F 是CD 的中点.（1）求CD 的长；（2）证明△EDF 是等边三角形.5、如图是某建筑物的屋顶架，其中AB=8米，D 是AB 的中点，BC ，DE 都垂直于AC.如果∠ABC=60°，那么BC ，DE ，CD 各是多少米？6、如图，在Rt △ABC 中，∠ACB=90°，ED 是线段AB 的垂直平分线，已知∠1=31∠ABC ，求∠A 的度数。

第55次数学作业2015年春季学期钟南附中七一班
填空：_____________________________________________________,称这两条直线互相垂直，其中一条直线叫做另一条直线的_________.它们的交点叫做____________.
两条直线相交不成直角时, 称其中一条直线叫做另一条直线的_________.它们的交点叫做____________.
___________________________，垂直于同一条直线的两直线________________.
___________________________，如果一条直线垂直于两条平行线中的一条，那么这条直线_______________另一条直线.
97页例1、在如图4-40的简易屋架中，BD ，AE ，HF 都垂直于CG ，若∠1＝60°，求∠2的度数.
98页例2、如图4-41，已知CD ⊥AB ，∠1＝∠2，求∠BEF 的度数.
练习1、如图，直线AB ，CD 相交于点O ，EO ⊥CD ，∠BOE ＝60°，求∠A 的度数.
2、如图，DA ⊥AB ，CD ⊥DA ，∠B ＝56°，求∠C 的度数.
102页习题4.5A 组
1、如图，直线AB ，CD 相交于点O ，OF ⊥CD 于点O ，求∠AOC+∠BOF 的度数.
1 2 E D B 图4-40 F C A H G 1 2 E D B 图4-41 F C A E D B O C A 第2题图 C D 第1题图 A B F D
B O
C A 第1题图。

第54次数学作业2015年春季学期钟南附中七一班
习题4.4A 组2、如图，AB ∥DC ，∠1＝∠2，那么直线EF 与GH 有什么关系？试说明理由.
4、如图，∠1＝∠2，CB 平分∠ACD 与∠ABD ，试指出图中有哪些直线平行，并说明理由.
5、如图，∠ADC ＝∠ABC ，DE 平分∠ADC ，BF 平分∠ABC ，∠1＝∠3，那么DE 与FB 平行吗？试说明理由.
6、教室后墙上有一个长方形的“阅读栏”.为了检验“阅读栏”的边是否与墙的边平行，可以采用哪些方法？
7、如图，∠1与∠3互余，∠2与∠3的余角互补，那么直线AB 与CD 有什么关系？试说明理由.
8、如图，（1）若∠1+∠3＝180°，能否得出AB ∥CD ？试说明理由.
（2）若∠2＝∠3，能否得出AB ∥CD ？试说明理由.
1 2 A 3 第2题图 B C D H G E F
1 2 A 第4题图 B C D
1 2 D 3 E A B C 第5题图 F 阅读栏 第6题图 1 2 A 第7题图 C B D 3 C F E A B D 3 1 2 4 第8题图。

数学作业本2015年春季学期钟南附中七一班第一次数学作业例：小玲在文具店买了3本练习本，2支圆珠笔，共花去8元，其中购买的练习本比圆珠笔多花4元.（1）为了知道练习本、圆珠笔的单价是多少元，你能列出相应的方程组吗？（2）⎩⎨⎧==12y x ，是列出的二元一次方程组的解吗？练习1、⎩⎨⎧==22y x ，是上例方程组的解吗？2、一条船顺流航行，每小时行24km ；逆流航行，每小时行18km.（1）为了求轮船在静水中的速度x 与水的流速y ，你能列出相应的方程组吗？（2）⎩⎨⎧==321y x ，是列出的二元一次方程组的解吗？3、⎩⎨⎧==12y x ，是下列哪个二元一次方程组的解？ （1）⎩⎨⎧=+=-；，5332y x y x （2）⎩⎨⎧=-=-.634243y x y x ，习题1.1A 组1、已知两个自然数的和是98，差是4. 设这两个自然数分别是x ，y （其中x ＞y ），请列出关于x ，y 的方程组.2、某项球类比赛，每场比赛须分出胜负，其中胜1场得2分，负1场得1分. 某队在全部15场比赛中得到26分，为了求出这个队胜负场数分别是多少，请列出相应的方程组.3、⎩⎨⎧==52y x ，是下列哪个二元一次方程组的解？ （1）⎩⎨⎧=+=-；，173255y x y x （2）⎩⎨⎧=-=+.13155y x y x ，B 组4、某灾区在地震后有9000灾民急需账篷居住. 某企业准备捐助甲、乙两种型号的帐篷共2000顶，其中甲种帐篷每顶可安置6人，乙种帐篷可安置4人. 设该企业捐助甲种帐篷x 顶，乙种帐篷y 顶，恰好安置全体灾民，列出求甲、乙各多少顶的方程组？5、甲、乙两人从相距6km 的A ，B 两地匀速相向而行，1h 后相遇.已知甲的速度比乙的速度快1km/h ，为了求出甲、乙的速度，请你列出相应的方程组。

6、某阶梯教室从第2排起，每一排都比前一排增加相同数目的座位.已知第5排有36个座位，第20排有66个座位.为了求出第一排有多少个座位，以及每一排比前一排多几个座位，你能列出相应的方程组吗？例1、解二元一次方程组⎩⎨⎧=+-=-.1395y x y x ，例2、用代入法解方程组⎩⎨⎧=-=-.175032y x y x ，练习1、把下列方程改写为用含x 的代数式表示y 的形式.（1）12-=-y x ； （2）022=-+y x .2、用代入法解下列二元一次方程组：（1）⎩⎨⎧=-=+.4128y x y x ， （2）⎩⎨⎧-==+.12523x y y x ，（3）⎩⎨⎧=+=+.731125b a b a ， （4）⎩⎨⎧=-+=+-.0332013n m n m ，习题1.2A 组1、解下列二元一次方程组：（1）⎩⎨⎧-==-.,2152x y y x （2）⎪⎩⎪⎨⎧+==+.12162s t t s ，例3用加减消元法解二元一次方程组⎩⎨⎧=-=+.832137y x y x ，例4、用加减消元法解二元一次方程组⎩⎨⎧=--=+.9561132y x y x ，练习用加减法解下列二元一次方程组：（1）⎩⎨⎧=+--=+.1832,22y x y x （2）⎩⎨⎧-=+=-.4351125b a b a ，（3）⎩⎨⎧-=-=+.4756823n m n m ， （4）⎩⎨⎧=+=-.3125,3442y x y x习题1.2A 组1、解下列二元一次方程组：（3）⎩⎨⎧-=+-=.7.3,32x y x y （4）⎩⎨⎧-=-=-.139513b a b a ，例5解二元一次方程组：⎪⎩⎪⎨⎧=+=-.432225n m n m ，例6解二元一次方程组：⎩⎨⎧-=+=+.134843y x y x ，例7、在方程b kx y +=中，当..3111的值和试求时，；当时，b k y x y x =-=-==练习1、解下列二元一次方程组： （1）⎪⎩⎪⎨⎧=-=+.6352132y x y x ， （2）⎩⎨⎧=+=-.31252452y x y x ，2、已知⎩⎨⎧==⎩⎨⎧=-=3201y x y x ，和，都是方程b ax y +=的解，求a 、b 的值.习题1.2A 组2、解下列二元一次方程组：（1）()()⎩⎨⎧=+--=-+.231522y y x y y x ， （2）⎪⎩⎪⎨⎧-=+-=-.133273132y x y x ，（3）⎩⎨⎧=--=++01327052n m n m （4）⎩⎨⎧=+=+13052y x y x（5）⎩⎨⎧-=+=-133432y x y x （6）⎩⎨⎧=+--=-875.4125.1q p q p3、当x =2，一2时，代数式b kx +的值分别是一2，一4，求k ，b 的值.习题1.2B 组4题解下列二元一次方程组：（1）⎩⎨⎧=--=+25351443y x y x ， （2）()()⎪⎩⎪⎨⎧=+--++-=-2352225n m n m n m ，5、有一个两位数，个位上的数比十位上的数大5，如果把这两个数的位置进行对换，那么所得的新数与原数的和是143. 求这个两位数.6、地球的表面积约为5.1亿平方千米，其中海洋面积约为陆地面积的2.4倍. 则地球上的海洋面积和陆地面积各是多少？7、从A 城到B 城的航线长1200km ，一架飞机从A 城飞往B 城，需要2小时，从B 城飞往A 城，需要2.5小时.假设飞机保持匀速，风速的大小和方向不变，求飞机的速度和风速.例1、某业余运动员针对自行车和长跑项目进行专项训练.某次训练中，他骑自行车的平均速度为10m/s ，跑步的平均速度为310m/s ，自行车路段和长跑路段共5km ，共用时15min.求自行车路段和长跑路段的长度.例2、某食品厂要配制含蛋白质15%的食品100kg ，现在有含蛋白质分别为20%，12%的甲乙两种配料. 用这两种配料可以配制出所要求的食品吗？如果可以的话，它们各需要多少千克？16页练习1、一块金与银的合金重250g, 放在水中称，减轻了16g . 已知金在水中称，金重减轻191；银在水中称，银重减轻101. 求这块合金中含金、银各多少克？2、甲、乙两种商品原来的单价和为100元，因市场变化，甲商品降价10%，乙商品提价40%，调价后两种商品的单价和比原来的单价和提高了20%. 求甲、乙两种商品原来的单价.习题1.3A 组1、小红买了80分与60分的邮票共17枚，花去12.2元.试问：80分与60分邮票各买了多少枚？例3、某城市规定：出租车起步价所包含的路程为0～3km ，超过3km 的部分按每千米另收费. 甲说：“我乘这种出租车走了11km ，付了17元. ”乙说：“我乘这种出租车走了23km ，付了35元.” 请你算一算：出租车的起步价是多少元？超过3km 后，每千米的车费是多少元？例4、某装订车间的工人要将一批书打包后送往邮局，其中每包书的数目相等.第一次他们领来这批书的127，结果打了14个包还多35本；第二次他们把剩下的书全部取来，连同第一次打包剩下的书一起，刚好又打了11包. 这批书共有多少本？18页练习1、星期日，小军与小明所在年级分别有同学去颐和圆和圆明园参观，其参观人数和门票要花费如下表，问：颐和园和圆明园的门票各是多少元？2、王先生家厨房需要更换地面瓷砖，他采用两种颜色的地砖搭配使用，其中彩色地砖24元每块，单色地砖12元每块，购买的单色地砖数比彩色地砖数的2倍少15块，买两种地砖共花去2220元. 求购买的彩色地砖数和单色地砖数.颐和园参观人数 圆明园参观人数 门票花费总计 小军所在年级 30 30 750元 小明所在年级 30 20 650元习题1.3A组2、小亮对小芬说：“我的生日的月和日相加是37，月的2倍和日相加是43.”小芬说：“这不可能啊！”你觉得小芬说得对吗？为什么？3、小英家今年1月份用水20t，交水费43元；2月份用水18t，交水费38元. 该城市实行阶梯水价，14t以内按正常收费，超出部分则收较高水费. 问：在限定量以内的水费每吨多少元？超出部分的水费每吨多少元？4、某企业向商业银行申请了甲、乙两种贷款，共计35万元，每年需要付出利息4.4万元.甲种贷款每年的利率是12%，乙种贷款的利率是13%. 求这两种贷款的金额各是多少？5、某水果公司收购某种水果104t，准备加工后上市销售. 该公司加工该种水果的能力是：每天可以精加工4t或粗加工8t. 现水果公司计划用16天完成这项加工任务，则应安排几天精加工？几天粗加工？B 组6、某农户种植核桃树和杏树，已知种植的核桃树棵数比总数的一半多11棵，种植的杏树棵数比总数的三分之一少2棵. 问这两种果树各种植了多少棵？7、某中学组织一批学生春游，原计划租用45座客车若干辆，但有15人没有座位；若租用同样数量的60座客车，则多出一辆车，且其余客车恰好坐满. 已知45座客车租金为每辆220元，60座客车租金为每辆300元，问：（1）这批学生的人数是多少？原计划租用多少辆45座客车？（2）若租用同一种车，要使每一位学生都有座位，应该怎样租用才合算？8、某天，一蔬菜经营户用60元从蔬菜批发市场购进西红柿和豆角共40kg 到菜市场去卖，西红柿和豆角这天的批发价、零售价（单位：元/kg ）如下表所示，问他当天卖完这些西红柿和豆角能赚到多少钱？9、如图，有一个正方形和一个长方形.若正方形的周长与长方形的周长相等，求： （1）x ，y 的值；（2）正方形和长方形的面积.品名 批发价 零售价 西红柿 1.2 1.8 豆角 1.6 2.512++y xy x 24-y x 32+13-x习题1.3B 组9题图例、解三元一次方程组⎪⎩⎪⎨⎧-=++=-+=++.2143045z y x z y x z y x ，，22、练习1解下列三元一次方程组：（1）⎪⎩⎪⎨⎧=-=+=+.7627z x z y y x ，， （2）⎪⎩⎪⎨⎧-=++=++=++.622722422z y x z y x z y x ，，2、有甲、乙、丙三人，若甲、乙的年龄之和为15岁，乙、丙的年龄之和为16岁，丙、甲的年龄之和为17岁，则甲、乙、丙三人的年龄分别是多少岁？引例、小丽家三口人的年龄和为80岁，小丽的爸爸比妈妈大6岁，小丽的年龄是爸爸和妈妈的年龄和的71.试问这家人的年龄分别是多少岁？习题1.4A 组1、解下列三元一次方程组：（1）⎪⎩⎪⎨⎧-=+-=+++=.62,12,1z y x z y x x y （2）⎪⎩⎪⎨⎧-=-=+=-.183,223,123x y y z z x2、解下列三元一次方程组：（1）⎪⎩⎪⎨⎧=++=++=+-.60525,324,0z y x z y x z y x （2）⎪⎩⎪⎨⎧=++=+-=+.932,8795,743c b a c b a b a3、当x =1，3，一2时，代数式c bx ax ++2的值分别为一9，一3，12，试求a ，b ，c 的值. 4、一个三位数是它各数位上数字之和的27倍. 已知百位上的数字与个位上的数字之和比十位上的数字大1. 如果把百位上的数字与个位上的数字交换位置，则所得的新数比原数大99.求这个三位数.习题5、今有上等谷3束，中等谷2束，下等谷1束，共39斗；上等谷2束，中等谷3束，下等谷1束，共34斗；上等谷1束，中等谷2束，下等谷3束，共26斗. 问上、中、下三等谷每束各是几斗？复习题1A 组1、分别用代入法和加减法解方程组：⎩⎨⎧=+=+.173,7y x y x2、解下列二元一次方程组： （1）⎩⎨⎧--=+=.123,132n m n m （2）⎩⎨⎧=+-=+.353,102y x y x（3）⎩⎨⎧=-=+.1232,1537y x y x （4）⎪⎩⎪⎨⎧+==+.221,623x y y x3、解下列二元一次方程组：（1）⎩⎨⎧-=-=+.1843,134y x y x （2）⎩⎨⎧=-+=+-.0275,02353n m n m5、晓玲想通过饮牛奶和橙汁来提高身体中钙和维生素A 的含量. 一盎司牛奶含38毫克钙和56微克维生素A ，一盎司橙汁含5毫克钙和60微克维生素A ，她每天应喝牛奶和橙汁各多少盎司，才能保证身体中每日摄入550毫克钙和1200微克维生素A ？6、小刚从今年2月初起刻苦练习跳高，每个月的跳高成绩都比上一个月有提高，而且提高的高度相同. 3月份，7月份他的跳高成绩分别为1.45m ，1.53m.你能算出他2月份的跳高成绩以及每个月提高的高度吗？7、大伟购买了一套经济适用房，户型图如图所示，他打算将地面铺上地砖，请根据图中的数据（单位：m ）回答下列问题：（1）写出用含x ，y 的代数式表示的地面面积. （2）已知客厅、餐厅面积之和比卫生间面积多 222m ，且地面总面积是卫生间面积的9.5倍， 铺12m 地砖的平均费用为85元，求铺地砖的总费用为多少元？8、小亮所在年级到某地参加自愿者活动. 车上准备了5箱矿泉水，每箱的瓶数相同. 到达目的地后，先从车上搬下2箱，发给每位自愿者1瓶矿泉水，有8位未领到. 接着又从车上搬下3箱，继续分发，最后每位自愿者都有2瓶矿泉水，还剩下8瓶.有多少人参加自愿者活动？每箱有多少瓶矿泉水？客厅卧室餐厅厨房卫生间 4 2 3xy 109、解下列三元一次方程组（1）⎪⎩⎪⎨⎧-=+-=+-=.332,22,2z y x z y x y x （2）⎪⎩⎪⎨⎧-=++=+--=++.324,0,4z y x z y x z y x10、解下列二元一次方程组：（1）()()⎪⎩⎪⎨⎧=+--=-+.223,33312yx y y x （2）()⎪⎩⎪⎨⎧=-+=-.035155,4632y x yx11、某城市一种出租车的起步价为10元，两位乘客分别乘这种出租车走了10km 和14km ，车费分别为21.2元和27.6元，且一路顺利，没有停车等候. 你能算出这种出租车起步价所允许行驶的最远路程吗？超过起步路程但行驶不到15km 时，超过部分每千米车费为多少元？（本题不考虑用计程器计费的某些特殊规定.）复习题1的12题、二元一次方程组⎩⎨⎧=+-=-.562,23y x y x 有解吗？13、二元一次方程组⎩⎨⎧-=+-=-.462,23y x y x 有解吗？14、在一次国际象棋女子挑战赛上，我国女子国际象棋特级大师谢军在苦战15盘后，以净胜俄罗斯棋手加里亚莫娃2分的优胜成绩，第三次夺得棋后桂冠.比赛的积分规则是胜得1分，负得0分，和棋各得0.5分. 问两位棋手最后的得分各是多少？填空：同底数幂相乘的法则是__________________________，公式是__________________.例1、计算：（1）351010⨯； （2）43x x ∙.例2、计算：（1）3a a ∙-； （2）1+∙n n y y （是正整数n ）例3、计算：（1）432333⨯⨯； （2）42y y y ∙∙.30页练习1、计算：（1）461010⨯ （2）35x x ∙ ；（3）4a a ∙； （4）44y y ∙.2、计算：（1）53222⨯⨯； （2）432x x x ∙∙；（3）55a a ∙-； （4）a a m∙（m 是正整数）；（5）11-+∙m m x x（其中是正整数，且＞m m 1）.习题2.1A 组1、填空（1）32a a ∙=_________； （2）43x x x ∙∙=_________.B 组12、填空 （1）12-∙m mx x=_________（m 是正整数）； （2）()是正整数n y y y n n =∙∙+12；（3）()()a a a -∙-∙-32=____________.填空：幂的乘方的法则是__________________________，公式是__________________. 例4、计算：（1）()2510； （2）()43a -.例5、计算：（1）()4m x （m 是正整数）； （2）()334a a ∙.32页练习1、填空：（1）()3410=_____________ ；（2）()33a =_____________ ； （3）()53x -=_____________ ； （4）()232x x ∙=____________.2、下面的计算对不对？如果不对，应怎样改正？ （1）()734a a =； （2）()923a a =.3、自编两道幂的乘方的运算题，并与同学交流计算过程与结果.习题2.1A 组2、计算（1）()32a （2）()5m x -（m 是正整数）.3、计算（1）()23a a ∙-； （2）()2x x -∙；（3）()()32x x -∙-； （4）()()()a a a-∙-∙-23.填空：积的乘方的法则是__________________________，公式是__________________. 例6、计算：（1）()32x -； （2）()24xy -；（3）()32xy ； （4）43221⎪⎭⎫⎝⎛-z xy .例7、计算：()()23332232b a b a -.34页练习1、计算：（1）321⎪⎭⎫ ⎝⎛x ； （2）()4xy-；（3）()322n m -； （4）()4323c ab -.2、下面的计算对不对？如果不对，应怎样改正？ （1）()623ab ab =； （2）()33362y x xy =.3、计算：()()222242z y x xyz +-.习题1.2A 组2、计算：（3）()322y x -； （4）()()是正整数n q p n2.单项式乘单项式的运算法则：______________________________________________________ 例8、计算：（1）()()y x y x 22332∙-；（2）()()b a a 2332-∙； （3）()⎪⎭⎫⎝⎛-∙+21412y x y xn n ()是正整数n .例9、天文学上计算星球之间的距离是用“光年”做单位的，1光年就是光在一年内所走过的距离.光的速度约为3810⨯m/s ，一年约为3710⨯s. 计算1光年约多少米.36页练习1、计算：（1）()⎪⎭⎫⎝⎛-∙z y x y x 22412； （2）()22242xy y x ∙-.2、下面的计算对不对？如果不对，应怎样改正？（1）6321234x x x =∙； （2）()42242x x x =∙-.3、计算()是正整数其中n ：（1）22421xy y x n ∙⎪⎭⎫ ⎝⎛-； （2）22421xy y x n ∙⎪⎭⎫ ⎝⎛- .习题2.1A 组4、计算：（1）ab a 323∙； （2）()2223xy y x -∙；（3）()()65103102⨯⨯； （4）()()74105.2102.1⨯⨯；（5）()()24108.01025.1⨯⨯b a .单项式乘多项式的运算法则：______________________________________________________例10、计算： （1）⎪⎭⎫ ⎝⎛+-∙121422x xy x ； （2）()ab a b 442122-∙⎪⎭⎫⎝⎛-.例11、求()()xy x y xy x -∙--∙-22244221的值，其中x =2，y =－1.37页练习1、计算（1）()y x x 522-∙-； （2）()x x x 4132∙+-；（3）()()x x 612-∙+； （4）()b a a 353-∙.2、先化简，再求值：⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛---x y x xy xy 214213222，其中x =－2，y =21.习题2.1A 组5、光的速度约为3810⨯m/s ，一年约为3710⨯s. 从太阳系外离地球最近的一颗恒星（比邻星）发出的光需要4年时间才能到达地球，求这颗恒星与地球的距离.多项式乘多项式的运算法则：______________________________________________________ _______________________________________________________________________. 例12、计算：（1）()()y x y x 32-+；（2）()()53122--+x x x ； （3）()()b x a x ++.例13、计算：（1）()()b a b a -+；（2）()2b a +； （2）()2b a -.40页练习1、下列计算对不对？如果不对，应怎样改正？ （1）()()()2262323b a b b a a b a b a -=∙-+∙=+-；（2）()()32331132+-=∙-+∙+∙=-+x x x x x x x x .2、计算：（1）()()32+-x x ； （2）()()51++x x ； （3）()()54-+x x ； （4）()23-x .3、计算：（1）()22y x +； （2）()()n m n m +-22；（3）()()b a b a 2323-+； （4）()223b a -.40页习题2.1A 组6、长方体的长是cm 4104.2⨯，宽是cm 3105.1⨯，高是cm 3106.0⨯， 求这个长方体的体积及表面积.7、计算：（1）()⎪⎭⎫⎝⎛+--1214222ab ab a ； （2）()xy xy y x 322∙-； （3）()()2232322---xy x xy x ； （4）()()mn m mn mn n m m +--222534.8、下列计算对不对？如果不对，应怎样改正？（1）()()22121418216723n n m m n m n m -+-=-+；（2）()()43224332222626432322y xy y x y xy xy y x y xy y xy ++=-+-=-+-.9、计算：（1）()()22-+x x ； （2）()()1212-+x x ； （3）()23n m +； （4）()22-x .10、计算：（1）()()()3214222-+--∙x x x x x ；（2）()()()a b a b a b a ∙---+23234.习题2.1A 组11、先化简，再求值：()()()()52342312---+-x x x x ，其中x =－21.B 组13、制作拉面需要将长条形面团摔匀拉伸后对折，并不断重复若干次这组动作.随着不断地对折，面条根数不断增加. 若一碗面有64根面条，则面团需要对折多少次？若一个拉面店一天能卖出2048碗拉面，用底数为2的幂表示拉面的总根数.14、计算：（1）()()222222y xyx -+； （2）()()22y xy x y x ++-.15、求如图所示的窗户的边框的面积（上部为半圆）.（单位：cm ）.10x +2120 x x15题图平方差公式：_________________________________________________________平方差公式的运算法则：_________________________________________________________例1、运用平方差公式计算：（1）()()1212-+x x ； （2）()()y x y x 22-+.例2、运用平方差公式计算：（1）⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛--y x y x 212212； （2）()()a b b a 44+-+.例3、计算：1002×998.44页练习1、下列计算对不对？如果不对，应怎样改正？ （1）()()2222-=+-x x x ；（2）()()1412122-=---x x x .2、运用平方差公式计算：（1）()()n m n m 22-+； （2）()()b a b a -+33；（3）⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛-y x y x 2121； （4）()()a a 5151--+-.3、计算：（1）202×198； （2）49.8×50.2.习题2.2A 组1、运用平方差公式计算：（1）()()y x y x -+22； （2）()()b a b a +---；（3）()()x x 2.01.01.02.0+-； （4）102×198.完全平方公式：_________________________________________________________完全平方公式的运算法则：______________________________________________________例4、运用完全平方公式计算：（1）()23n m +； （2）221⎪⎭⎫ ⎝⎛-x .46页练习1、下列各式计算对不对？如果不对，应怎样改正？（1）()4222+=+x x ； （2）()2222b ab a b a +-=--.2、运用完全平方公式计算：（1）()24+x ；（2）()232-a ； （3）2215⎪⎭⎫ ⎝⎛-m .习题2.2A 组2、运用完全平方公式计算：（1）()245b a +； （2）()223y x -.复习题2A 组2、计算：（1）⎪⎭⎫ ⎝⎛+-y x xy 21316;（2）()m mn m 3215-∙⎪⎭⎫⎝⎛-； （3）()()152-+a a .3、计算：（1）()()22-+x x ； （2）()()a a 3113+---； （3）()252+m ； （4）()223y +-.公式处理：()=-2a b ______________，()=--2b a ______________.例5、运用完全平方公式计算：（1）()21+-x ； （2）()232--x .例6、计算：（1）()()22b a b a --+； （2）()21++b a .例7、计算：（1）2104； （2）2198.47页练习1、运用完全平方公式计算：（1）()232+-a ； （2）2213⎪⎭⎫ ⎝⎛+-x ；（3）()224y x --； （4）()221b -.2、计算：（1）()()2222y x y x --+； （2）()21+-b a .3、计算：（1）2103； （2）2297.习题2.2A 组3、运用乘法公式计算：（1）()()22---x x ； （2）()221--x x ；（3）221⎪⎭⎫ ⎝⎛+a －221⎪⎭⎫ ⎝⎛-a ； （4）()()11+--x x .引例：计算：（1）()()()1112-++x x x ； （2）()()11-+++y x y x .例8、运用乘法公式计算：（1）()()[]233-+a a ； （2）()()c b a c b a -++-.例9、一个正方形花圃的边长增加到原来的2倍还多1m ，它的面积就增加到原来的4倍还多21平方米，求这个正方形花圃原来的边长.48页练习1、运用乘法公式计算：（1）()()()4222++-x x x ； （2）()()1212++-+b a b a ；（3）()()1212+--+n m n m ； （4）()()2211-+x x .2、计算：()2c b a --.3、一个正方形的边长增加2cm ，它的面积就增加16平方厘米，求这个正方形原来的边长.习题2.2A 组4、计算：（1）()()()()y x y x y x y x 232322-+-+-；（2）()()()2222b a b a b a --+-.习题2.2B 组5、运用乘法公式计算：（1）()()z y x z y x 3232+--+； （2）()212-+y x .6、先化简，再求值：()()()22422y x y x y x +-+，其中21=x ，31=y .7、求下图的面积：8、已知()492=-b a ，18=ab ，求代数式22b a +的值.9、已知甲数为a 2，乙数比甲数的2倍多3，丙数比甲数的2倍少3，求甲、乙、丙三个数的积. 当31-=a 时，积是多少？复习题2A 组4、计算：（1）()()()2333+--+x x x ； （2）()()z xy z xy +-+；（3）()()1212+--+y x y x .6、用乘法公式计算：5014995002⨯-.第7题图b a -2a2b复习题2A 组1、计算：（1）3b b ∙-； （2）()432a a a -∙∙；（3）()2x x -∙-； （4）()322b a -；（5）()xy x 25-∙； （6）()22231xy xy -∙⎪⎭⎫ ⎝⎛-.5、先化简，再求值：（1）()y x x x 2242+--，其中1-=x ，2=y ；（2）()()()2222y x y x y x --+-，其中2-=x ，21=y .7、已知甲数为a ，乙数比甲数的2倍多1，丙数比乙数少2，求甲、乙、丙三个数的和与积. 当25-=a 时的和与积分别是多少？8、如图，把边长为a 的正方形的四角，各剪去一个边长为⎪⎭⎫ ⎝⎛2a b b ＜的正方形，然后把它折成一个无盖的纸盒，求纸盒的容积.（结果要求用关于a 、b 的多项式表示.）复习题2B 组9、已知()()4,922=-=+b a b a .求：（1）ab 的值； （2）22b a +的值.第8题图 a53页复习2B 组10、计算：（1）()[]322223---x x x x ； （2）()()112++-x x x .11、解下列方程（组）：（1）()()()()523211-=-+-+-x x x x x ； （2）()()⎩⎨⎧=-=-+.422212y x xy y x ，12、先化简，再求值： （1）()⎥⎦⎤⎢⎣⎡+--y x y x xy 2122，其中3-=x ，32=y ； （2）()()()()222b a b a b a b a -++--+，其中2=a ，21=b .C 组13、解方程：()()294152222-+-=--+x x x x .复习题2C 组53页14、计算：（1）()()22b ab a b a +-+； （2）()()22b ab a b a ++-；（3）()3b a +； （4）()3b a -.15、求值： （1）已知31=+a a ，求221a a +和441aa +的值；（2）已知2=-b a ，1=ab ，求22b a +的值.16、把一个边长为c b a ++的正方形按如图所示分割成9块，你能用这个图来解释()bc ac ab c b a c b a 2222222+++++=++吗？aa2aabac复习题2C 组16题图2b2cabacbcbc填空：______________________________________________________，称为把这个多项式因式分解.例1、下列各式由左边到右边的变形，哪些是因式分解，哪些不是，为什么？ （1）()2222b a b ab a +=++；（2）()()22342+-+=-+m m m m .例2、检验下列因式分解是否正确. （1）()y x x xy x +=+2；（2）()()32652--=+-a a a a ；（3）()()n m n m n m +-=-22222.57页练习1、求4，6，14的最大公因数.2、下列各式由左边到右边的变形，哪些是因式分解，哪些不是，为什么？ （1）()()23212++=++x x x x ； （2）()y x xy xy y x 224222+=+；（3）()()11122--+=-x x x ；（4）()2212144-=+-a a a .3、检验下列因式分解是否正确. （1）()22422+-=+-a a a a ；（2）()x x x x x x +=++223；（3）()()21232++=++m m m m .习题3.1A 组1、求36和60的最大公因数.2、下列各式由左边到右边的变形，哪些是因式分解，哪些不是，为什么？ （1）()1241842--=--x x x x ；（2）()122--=--bx ax x x bx ax ；（3）()()1122--+=--y x y x y x .3、检验下列因式分解是否正确. （1）()()521072--=--x x x x ；（2）()141442-=+-m m m m ；（3）()y x xy xy y x -=-2551022；（4）()b ab a a b a b a -=+-222223.B 组4、下列各式由左边到右边的变形，哪些是因式分解，哪些是多项式乘法？ （1）()()54152-+=-+x x x x ； （2）()()4222-=-+x x x ；（3）()y x a ay ax -=-121212； （4）()22252510y x y xy x -=+-.5、小明在水果店里买了苹果、梨、葡萄各a kg ，这三种水果的单价分别为z y x ,,元. （1）用两种方法计算他共花了多少元？（2）在你得到的两个式子中，分别要做多少次加法，多少次乘法？按照哪个式子计算较简便？（3）你能从这个例子中体会到因式分解的用处吗？填空：__________________________________________________________________ ____________________________________叫做提公因式法. 例1、把x xy x +-352因式分解.例2、把x x 642-因式分解.例3、把z xy y x 242128-因式分解.练习1、说出下列多项式中各项的公因式： （1）y xy y x 1518122-+-； （2）32r h r ππ+；（3）()的整数均为大于1,4211n m y x y x n m n m ---.2、在下列括号内填写适当的多项式： （1）()x x x x =+-2323;（2）()y x yz x y x 222364830-=+-.3、把下列多项式因式分解： （1）y y xy +-253; （2）2232231046n m n m n m +--; （3）32442231284z y x yz x yz x +-.习题3.2A 组1、在下列括号内填写适当的多项式： （1）()x xy x x 2101022-=-+-;（2）()232313231r r h r πππ=+.2、把下列多项式因式分解：（1）x x 1042+-; （2）y xy y --532;（3）2232362115b a b a b a +-.例4、把下列多项式因式分解： （1）()()232---x x x ； （2）()()x x x ---232.例5、把()()()()22a b c a b a c a ----+因式分解.例6、把()()y x y x y x xy +-+221812因式分解.62页练习1、把下列多项式因式分解： （1）()()y x x y x y -+-； （2）()()x y x y x y -+-； （3）()()22x y b y x a ---；（4）()()b a ab b a b a ---2264. 习题3.2A 组2、把下列多项式因式分解： （4）()()()()111122++++++-x x x x x x ；（5）()()()()b a b a b a b b a a -+--+； （6）()().3624232223b a b a b a b a +-+.B 组3、把下列多项式因式分解： （1）()()623---y y x ； （2）()()()y x y x y x +--+23；（3）()()xy x xy x x 4422---.4、从一座楼房的房顶掉下一个小球，经过某个窗户下边框时的速度s m v /75.20=，再经过2.5s ，小球着地.已知小球降落的高度h 满足公式：2021gt t v h +=，其中2/8.9s m g =，t 为小球下落的时间，求该窗户下边框离地的高度.怎样计算较简便？____________________________________________________叫做公式法. 例1、把22425y x -因式分解.例2、把()()22y x y x --+因式分解.例3、把44y x -因式分解.例4、把523x y x -因式分解. 64页练习1、填空： （1）()229=y ； （2）()222536=x ； （3）()2249=t .2、把下列多项式因式分解： （1）2249x y -； （2）2251x -； （3）2216259n m -； （4）()()22x y y x --+； （5）164-x ； （6）24369y x -； （7）23ab a -.3、计算：（1）224.506.49-； （2）227.113.13-.4、手表表盘的外圆直径D ＝3.2cm, 内圆直径d ＝2.8cm ，在外圆与内圆之间涂有防水材料.试求涂上防水材料的圆环的面积（结果保留π）.怎样计算简便？例5、把41392+-x x 因式分解例6、把.229124y xy x -+-因式分解.例7、把2242b b a a ++因式分解.例8、把1224+-x x 因式分解.66页练习1、填空（若某一栏不适用，填入“不适用”）：多项式能否表示成()2b a +或()2b a -的形式 a 、b 各表示什么25102+-x x 422++x x412y y ++229124y xy x +-2、把下列多项式因式分解： （1）42552++x x ；（2）924162+-y y ；（3）91322++x x ；（4）42234363y x y x x ++.66页习题3.3A 组1、把下列各式因式分解： （3）()2592--y x ；（4）()()22222---y yx ；（5）814-x ； （6）2633x x -；（7）()()222212b b a ---.2、把下列各式因式分解： （1）44972++x x ；（2）25102+-m m ；（3）2242025y xy x ++；（4）2241q pq p +-；（5）224914y xy x -+-；（6）4224168y y x x +-；（7）4424++x x .3、在边长为a 的正方形空地中间，有一个边长为2b （a >2b）的正方形水池. 若在空地上种草，试问：草地的面积是多少？如是a ＝124m ，b ＝48m ，那么草地的面积是多少？怎样计算较简便？习题3.3A 组1、把下列多项式因式分解： （1）812-x ； （2）2241b a -；习题3.3 B 组4、把下列多项式因式分解： （1）()12422+--y y x ；（2）()224444y x x -++；（3）()()x x x 314++-；（4）()()36122++++y x y x .5、已知1692++xm m 可以用完全公式进行因式分解，求x .6、在日常生活中，如取款、上网都需要密码. 有一种用因式分解产生的密码，方便记忆. 其原理是：对于多项式44y x -，其因式分解的结果是()()()y x y x yx -++22，若取9=x ，9=y ，则各个因式的值是0,18,16222=-=+=+y x y x y x ，于是就把“162180”作为一个六位数的密码. 对于多项式23xy x -，若取21=x ，5=y ，用上述方法产生的密码是多少？69页复习题3A 组1、把下列多项式因式分解： （1）x xy x +-2； （2）mn mn n m +-22；69页复习题3A 组1、把下列多项式因式分解： （3）22233312219y x y x y x +-； （4）()()y x y y x x -+-22. 2、把下列多项式因式分解： （1）92-x ； （2）228149n m -；（3）14412-x ； （4）2225191b a -； 3、把下列多项式因式分解： （1）252042++x x ； （2）9624++x x ； （3）811824+-x x ；（4）()()222w w y x y x +-+-；（5）42249124b b a a ++.4、把下列多项式因式分解： （1）61262-+-x x ；（2）2216249y xy x -+-；（3）()()()b a b b a ab b a a -+-+-222；（4）()()2211+--++y x y x ；（5）164-x ；（6）4416y x -.复习题3A 组5、计算：（1）11.04611.03711.017⨯+⨯+⨯； （2）22156256-.B 组6、把下列多项式因式分解： （1）()251022+--x x y ；（2）()()b a b a 3922-+-；（3）()()123-+-x x x ；（4）by ay bx ax +--.7、把下列多项式因式分解：（1）()()()()y x a b y x b a +--+-；（2）z xy yz x z x 22344+-.8、一种混凝土排水管，其形状为空心的圆柱体，它的内径d ＝68cm ，外径D ＝88cm ，长h ＝200cm. 浇制一节这样的排水管需要多少立方米的混凝土（结果保留π）？怎样计算较简便？9、先化简，再求值：()()()()222b a b a b a b a -+-+++，其中21=a ，b=1.10、已知312=-x ，求代数式()()13232+---x x 的值.复习题3C 组11、把下列多项式因式分解： （1）y x y x 2422++-；（2）()()142-+-+y x y x ；（3）112-++-n n n x x x （n 是大于1的正整数）.12、你能把多项式652++x x 因式分解吗？（1）上式能利用完全平方公式进行因式分解吗？（2）常数项6是哪两个因数的乘积？一次项系数5是否等于6的某两个因数的和？（3）由多项式乘法，()()()ab x b a x b x a x +++=++2，将该式从右到左地使用，即可对形如()ab x b a x +++2的多项式进行因式分解.多项式()ab x b a x +++2的特征是二次项系数为1，常数项为两数之积，一次项系数为这两个数的和.你能据此将652++x x 两个一次多项式的乘积吗？()()()++=⨯+++x x x x 2.请把填上数后的两个一次多项式相乘，验证乘积是否等于652++x x .（4）从第（3）小题，你能看出把652++x x 进行因式分解的关键步骤是什么吗？（5）你能运用上述方法将多项式22--x x 进行因式分解吗？第45次数学作业填空：__________________________________________________________叫做平行线. 平行公理：____________________________________________________________.平行于__________________________________的两条直线平行.74练习1、如图，在同一平面内，若AB ∥CD ，EF 与AB 相交于点P ，EF 能与CD 平行吗？为什么？75页练习2、请举出生活中平行的例子.3、请你用画平行线的方法画一件“艺术品” .习题4.1A 组 1、填空：（1）在同一平面内的两条直线若相交，则有_________个公共点； 若平行，则有_________个公共点.（2）在同一平面内，如果直线a 与b 相交，且直线a 与c 平行，则这三条直线中所有交点的个数为___________个.2、在同一平面内的两条射线AB 和CD ，如果它们不相交，能否说这两条射线平行？请画图说明.3、如图，用三角尺和直尺，过点C 画CD ∥AB.第46次数学作业填空：如果一个角的两边分别是另一个角的两边的___________，这样的两个角叫做对顶角. 对顶角的性质：____________________.ABC第3题图•A B CDE F P第1题图两条直线被第三条直线所截，同位角：这两个角在________直线的同侧，并且在这两条直线的_____________.内错角：这两个角在________直线的两侧，并且在这两条直线的_________. 同旁内角：这两个角在________直线的同侧，并且在这两条直线的_________.例1、如图，4-10，直线EF 与AB 相交，构成8个角.指出图中所有的对顶角、同位角、内错角和同旁内角.例2、如图4-11，直线AB ，CD 被直线MN 所截，同位角∠1与∠2相等，那么内错角∠2与∠3相等吗？练习1、举出生活中对顶角的例子.2、如图，工人师傅用对顶角量角器量工件a ，b 边所夹的角，其中∠1的度数可以从仪器上读出.试说明∠1就是所求角的理由.3、如图，直线a ，b 被直线c 所截，找出图中所有的对顶角、同位角、内错角和同旁内角.若∠1＝∠5＝108度，求其他角的度数.第47次数学作业习题4.1A 组4、如图，三条直线AB ，CD ，EF 相交于点O ，填空： （1）∠DOB 的对顶角是__________________；abc3 214 65第3题图aOb2 第2题图1A CDNM3 2 图4-11B1 AC DFE12 3 4 65 7 8 图4-10B（2）∠DOF 的对顶角是__________________； （3）∠DOA 的对顶角是__________________；5、如图，三条直线AB ，CD ，EF 相交于点O ，已知∠BOC ＝90度，OF 是∠BOC 的平分线，求∠AOE ，∠EOB 的度数.6、如图，指出下列各对角是什么角，它们分别是由哪两条直线被哪一条直线所截得到的. （1）∠2与∠3； （2）∠1与∠3.7、如图，在括号中填写理由： 已知∠1＝∠2，因为∠2＝∠4（ ）， 所以∠1＝∠4（ ）. 若∠1＝∠5＝108度，求其他角的度数.第48次数学作业 79页习题4.1B 组8、如图，工人师傅要测出一座建筑物两面墙的夹角∠ABC 的大小，但不能进入建筑物内部abc2143 第7题图ADCB E FO第5题图ABCDE FO第4题图1 32 A B C D 第6题图测量，你有什么办法吗？9、两条直线被第3条直线所截，如果有一对内错角相等（或同旁内角互补），你能得出同位角相等的结论吗？10、如图，在图中分别找出一个角与∠α配对，使两个角成为 （1）同位角； （2）内错角；（3）同旁内角.并指出它们分别是由哪两条直线被哪一条直线所截得到的.第49次数学作业填空：________________________________________________________________________ 叫做平移.________________叫做原像，______________________叫做该图形在平移下的像.AC第7题图BαA B第10题图DE CF G H平移的性质：1、_________________________________________________________________. 平移的性质2、_________________________________________________________________. _________________________________________________________________. 81页练习1、请举出生活中应用“平移”的例子. 2、如图，∠B O A '''是由∠AOB 平移得到的，说一说，∠B O A '''与∠AOB 的大小有什么关系？两个角的边有什么关系？84页习题4.2A 组1、填空：我们已经学过用三角尺画平行线的方法.如图，因为直线AB 沿 ______的方向______到CD ，且CD 经过点P ，由于直线在平移下的像是与它__________，所以AB____CD.2、如图，用第1题的方法，过图中的点A 画AE ∥BC.3、将三角形ABC 沿OM 方向平移一定的距离得到三角形C B A '''，则下列结论中不正确的是（A ）A A '∥B B ' （B ）A A '＝B B '（C ）C B BC ''= （D ）∠ACB ＝∠C B A '''. 两个角的边有什么关系？第50次数学作业 填空：平行线的性质1、___________________________________， 平行线的性质2、___________________________________，A 'B 'O 'A B 第2题图OD C A B第1题图C D A B 第2题图 C ' B ' A B 第3题图C A '平行线的性质3、___________________________________，87页，例1、如图4-24，直线AB ，CD 被直线EF 所截，AB ∥CD ，∠1＝100度，求∠3的度数.例2、如图4-25，AD ∥BC ，∠B ＝∠D ，∠A 与∠C 相等吗？为什么？88页练习1、如图，AB ∥CD ，CD ∥EF ，BC ∥ED ，∠B ＝70度，求∠C ，∠D ，∠E 的度数.2、如图4-24，直线AB ，CD 被直线AE 所截，AB ∥CD ，∠1＝105度，求∠2，∠3，∠4的度数.习题4.3A 组1、填空：如图，（1）因为AB ∥CD ，所以∠1＝_________，理由是_________ __________；（2）因为AB ∥CD ，所以∠D ＝_________，理由是_______________________.第51次数学作业习题4.3A 组2、如图，一条公路两次转弯后又回到与原来相同的方向，如果第一次转弯时321 B图4-24C DE F 2 1C习题第1题图 BAD124D第2题图 C BE3AAB第1题图CDEFBCDAA图4-25。

第45次数学作业2015年春季学期钟南附中七一班
填空：__________________________________________________________叫做平行线. 平行公理：____________________________________________________________. 平行于__________________________________的两条直线平行.
74练习1、如图，在同一平面内，若AB ∥CD ，EF 与AB 相交于点P ，EF 能与CD 平行吗？为什么？
75页练习2、请举出生活中平行的例子.
3、请你用画平行线的方法画一件“艺术品” .
习题4.1A 组
1、填空：
（1）在同一平面内的两条直线若相交，则有_________个公共点； 若平行，则有_________个公共点.
（2）在同一平面内，如果直线a 与b 相交，且直线a 与c 平行，则这三条直线中所有交点的个数为___________个.
2、在同一平面内的两条射线AB 和CD ，如果它们不相交，能否说这两条射线平行？请画图说明.
3。

第61次数学作业2015年春季学期钟南附中八一班
134页例1、甲、乙两地相距40km ，小明8：00点骑自行车由甲地去乙地，平均车速为8km/h ；小红10：00坐公共汽车也由甲地去乙地，平均车速为40km/h. 设小明所用时间为()h x ，小明与甲地的距离为()km y 1，小红离甲地的距离为()km y 2.
（1）分别写出1y ，2y 与x 之间的函数表达式；
（2）在同一直角坐标系中，画出这两个函数的图像，并指出谁先到达乙地.
练习1、某音像店对外出租光盘的收费标准是：每张光盘在出租后头两天的租金为0.8元/天，以后每天收0.5元. 求一张光盘在租出后第n 天的租金y （元）与时间t （天）之间的函数表达式.
2、某移动公司对于移动话费推出两种收费方式：
A 方案：每月收取基本月租费25元，另收通话费为0.36元/min ；
B 方案：零月租费，通话费为0.5元/min.
（1）试写出A ，B 两种方案所付话费y （元）与通话时间t （分钟）之间的函数表达式.
（2）分别画出这两个函数的图像；
（3） 若林先生每月通话30分钟，他选择哪种付费方式比较合算？。

2015年春季学期钟南附中八一班数学作业本第一次数学作业例1、如图1-5，已知CD是△ABC的AB边上的中线，且CD=0.5AB.求证：△ABC是直角三角形.练习1、在Rt△ABC中，斜边上的中线CD=2.5cm，则斜边AB的长是多少？2、如图，AB∥CD，∠CAB和∠ACD的平分线相交于H点，E为AC的中点，EH=2. 那么△AHC是直角三角形吗？为什么？若是，求出AC的长.习题1.1A组1，如图，CD是Rt△ABC的中线，∠ACB=90°，∠CDA=120°，求∠B的度数例2、如图1-8，在A 岛周围20海里水域内有暗礁，一轮船由西向东航行到O 处时，测得A 岛在北偏东60°的方向，且与轮船相距303海里. 若该船继续保持由西向东的航向，那么有触礁的危险吗？练习1、如图是某商店营业大厅电梯示意图. 电梯AB 的倾斜角为30°，大厅两层之间的高度BC 为6m.你能算出电梯AB 的长度吗？2、如图，在Rt △ABC 中，∠ACB=90°，CD 垂直于AB ，垂足为点D ，DB=0.5BC ， 求∠A 的度数.习题1.1A 组2、如图，在△ABC 中，已知∠B=21∠A=31∠C ，AB=8cm. （1）求证：△ABC 为直角三角形；（2）求AB 边上的中线长.习题1.1A 组3题如图，线段AE 与BC 相交于点D ，BD=CD ，AD=ED ，CA ⊥AE ， ∠1=30°，且AB=3cm. 那么线段BE 多长呢？4、如图，在Rt △ABC 中，∠ACB=90°，∠B=30°，AB=2，CD 是斜边上的中线，CE 是高，F 是CD 的中点. （1）求CD 的长；（2）证明△EDF 是等边三角形.5、如图是某建筑物的屋顶架，其中AB=8米，D 是AB 的中点，BC ，DE 都垂直于AC. 如果∠ABC=60°，那么BC ，DE ，CD 各是多少米？6、如图，在Rt △ABC 中，∠ACB=90°，ED 是线段AB 的垂直平分线，已知∠1=31∠ABC ，求∠A 的度数。

2015年春季学期钟南附中八一班数学作业本 第一次数学作业例1、如图1-5，已知CD 是△ABC 的AB 边上的中线，且CD=0.5AB. 求证：△ABC 是直角三角形.练习1、在Rt △ABC 中，斜边上的中线CD=2.5cm ，则斜边AB 的长是多少？2、如图，AB ∥CD ，∠CAB 和∠ACD 的平分线相交于H 点，E 为AC 的中点，EH=2. 那么△AHC 是直角三角形吗？为什么？若是，求出AC 的长.习题1.1A 组1，如图，CD 是Rt △ABC 的中线， ∠ACB=90°，∠CDA=120°，求∠B 的度数1 2 AB CD图1-5 H E A B C D第2题图1 2ABCD习题1.1第1题图例2、如图1-8，在A 岛周围20海里水域内有暗礁，一轮船由西向东航行到O 处时，测得A 岛在北偏东60°的方向，且与轮船相距303海里. 若该船继续保持由西向东的航向，那么有触礁的危险吗？练习1、如图是某商店营业大厅电梯示意图. 电梯AB 的倾斜角为30°，大厅两层之间的高度BC 为6m.你能算出电梯AB 的长度吗？2、如图，在Rt △ABC 中，∠ACB=90°，CD 垂直于AB ，垂足为点D ，DB=0.5BC ， 求∠A 的度数.习题1.1A 组2、如图，在△ABC 中，已知∠B=21∠A=31∠C ，AB=8cm. （1）求证：△ABC 为直角三角形；（2）求AB 边上的中线长.60° O 北 东ABD 303 30°A 练习1题图B 6mC A练习2题图 B C D B习题1.1A 组2题图AC习题1.1A 组3题如图，线段AE 与BC 相交于点D ，BD=CD ，AD=ED ，CA ⊥AE ， ∠1=30°，且AB=3cm. 那么线段BE 多长呢？4、如图，在Rt △ABC 中，∠ACB=90°，∠B=30°，AB=2，CD 是斜边上的中线，CE 是高，F 是CD 的中点. （1）求CD 的长；（2）证明△EDF 是等边三角形.5、如图是某建筑物的屋顶架，其中AB=8米，D 是AB 的中点，BC ，DE 都垂直于AC. 如果∠ABC=60°，那么BC ，DE ，CD 各是多少米？6、如图，在Rt △ABC 中，∠ACB=90°，ED 是线段AB 的垂直平分线，已知∠1=31∠ABC ，求∠A 的度数。

第72次数学作业2015年春季学期钟南附中七一班
152页习题6.2A组2、一个小组有8名同学，分别测量同一根绳子的长度，测得的数据（单位：cm）如下：
109.7，110.1，109.9，109.9，110，110.1，110.2，110.1.
（1）如何确定这根绳子的长度的近似值？
（2）如何评价测量的准确程度？
3、某村引进两种水稻良种，在条件（肥力、日照、通风……）不同的6块试验田中同时播种并核定亩产，其结果（单位：kg/亩）统计在下面的表中：
编号 1 2 3 4 5 6
甲550 560 550 525 555 560
乙545 580 575 525 530 545
问：哪个品种的产量较稳定，适合推广？
B组4、甲、乙两地的月平均气温（单位：℃）如下表所示：
月份 1 2 3 4 5 6 7 8 9 10 11 12 甲-8 -6 -2 8 13 18 21 19 14 7 -2 -4 乙11 13 17 20 23 25 28 27 25 20 17 14 试求甲、乙两地月平均气温的方差，并对两地气温变化情况作出比较.
5、某公司准备盖大楼，有两块土地可供征用，但两块土地都崎岖不平，需要平整. 现对每块土地确定房基基准高度，然后在两块土地上分别适当地另取10点，用水平仪测得各点对基准的相对标高（单位：cm）如下表所示：
编号 1 2 3 4 5 6 7 8 9 10
甲-45 76 47 -26 135 84 -61 -38 76 92
乙74 120 100 -70 -44 95 63 -50 57 -25 问：哪一块土地比较容易平整？。