下载文档原格式
京师微课ＪＩＮＧＳＨＩＷＥＩＫＥ
（上接第１７页）
立安排自己的学习时间，才能彻底激发学生的学习热情，使其主动地进行学习。
还要培养学生独立走上讲台的能力，给学生更广阔的舞台，促进学生的交流沟通，有助于培养学生良好的分析能力和表达能力，为学生的全面发展奠定基础。
（三）加快体育教学的内容改革
我国的高校体育教学仍然停留在传统的教学阶段，改革力度较低，不能挖掘潜在的教学能力。
在这次教学变革中应该积极推进体育线上教学的改革，向深层次和多元化角度进行全面发展，利用互联网技术的优势，培养更多的全面体育人才。
体育线上教学的目标就是培养更多符合社会发展的人才，实现体育的宗旨。
开展体育教学的过程中必须融入更多线上教育技术，才能取得体育的丰硕成果，培养更多的体育合格人才。
三、结语
高校线上教学模式的发展为培养体育人才提供支撑，引领高校教学发展的新模式，特别是使用网络教学授课，改变了传统高校体育教学的不足，打破了教学形式的限制，为高校改革提供了更多的支持。
教育工作者应该运用更多的教学模式，为培养更多的合格体育人才做出贡献。
参考文献
［１］任鹏．关于“互联网＋”背景下高校体育信息化教学改革的研究［Ｊ］．当代体育科技，２０２０（３０）．
［２］丁铮锴，许水生．体育教学模式、组织形式和教学方法创新［Ｊ］．中外企业家，２０２０（１７）．
·
３
５
·。
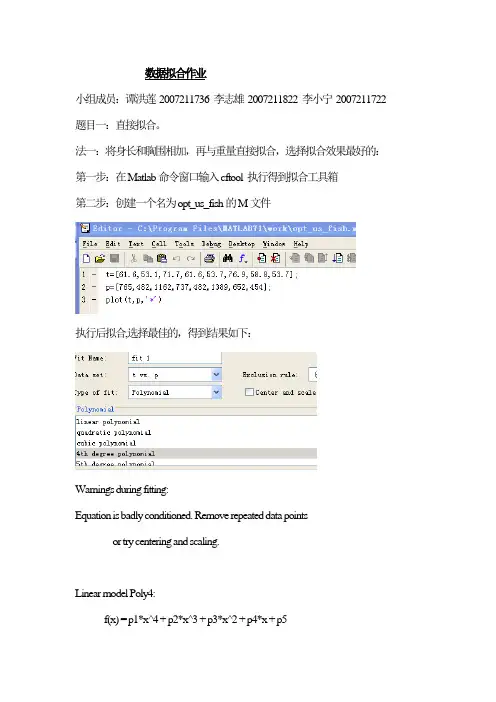
数据拟合作业小组成员：谭洪莲 2007211736 李志雄 2007211822 李小宁 2007211722 题目一：直接拟合。
法一：将身长和胸围相加，再与重量直接拟合，选择拟合效果最好的：第一步：在Matlab命令窗口输入cftool 执行得到拟合工具箱第二步：创建一个名为opt_us_fish的M文件执行后拟合,选择最佳的，得到结果如下：Warnings during fitting:Equation is badly conditioned. Remove repeated data pointsor try centering and scaling.Linear model Poly4:f(x) = p1*x^4 + p2*x^3 + p3*x^2 + p4*x + p5Coefficients (with 95% confidence bounds):p1 = 6.9e-011 (-2.238e-010, 3.618e-010) p2 = -2.549e-007 (-1.344e-006, 8.346e-007) p3 = 0.0003309 (-0.001117, 0.001778) p4 = -0.151 (-0.9579, 0.6559)p5 = 74.47 (-84.11, 233.1)Goodness of fit:SSE: 1.161R-square: 0.9979Adjusted R-square: 0.995RMSE: 0.6221拟合结果：法二：将身长与胸围相乘，再与重量直接拟合，选择拟合效果最好的，结果如下：（步骤同上）Warnings during fitting:Equation is badly conditioned. Remove repeated data pointsor try centering and scaling.Linear model Poly4:f(x) = p1*x^4 + p2*x^3 + p3*x^2 + p4*x + p5Coefficients (with 95% confidence bounds):p1 = 3.195e-009 (-4.077e-009, 1.047e-008)p2 = -1.164e-005 (-3.87e-005, 1.542e-005) p3 = 0.01518 (-0.02077, 0.05113)p4 = -7.549 (-27.59, 12.49)p5 = 1935 (-2004, 5874)Goodness of fit:SSE: 716.1R-square: 0.9986Adjusted R-square: 0.9968RMSE: 15.45拟合效果：题目二：首先利用机理分析建立模型。
数学建模方法大汇总数学建模是数学与实际问题相结合，通过建立数学模型来解决实际问题的一种方法。
在数学建模中，常用的方法有很多种，下面将对常见的数学建模方法进行大汇总。
1.描述性统计法：通过总结、归纳和分析数据来描述现象和问题，常用的统计学方法有平均值、标准差、频率分布等。
2.数据拟合法：通过寻找最佳拟合曲线或函数来描述和预测数据的规律，常用的方法有最小二乘法、非线性优化等。
3.数理统计法：通过样本数据对总体参数进行估计和推断，常用的方法有参数估计、假设检验、方差分析等。
4.线性规划法：建立线性模型，通过线性规划方法求解最优解，常用的方法有单纯形法、对偶理论等。
5.整数规划法：在线性规划的基础上考虑决策变量为整数或约束条件为整数的情况，常用的方法有分支定界法、割平面法等。
6.动态规划法：通过递推关系和最优子结构性质建立动态规划模型，通过计算子问题的最优解来求解原问题的最优解，常用的方法有最短路径算法、最优二叉查找树等。
7.图论方法：通过图的模型来描述和求解问题，常用的方法有最小生成树、最短路径、网络流等。
8.模糊数学法：通过模糊集合和隶属函数来描述问题，常用的方法有模糊综合评价、模糊决策等。
9.随机过程法：通过概率论和随机过程来描述和求解问题，常用的方法有马尔可夫过程、排队论等。
10.模拟仿真法：通过构建系统的数学模型，并使用计算机进行模拟和仿真来分析问题，常用的方法有蒙特卡洛方法、事件驱动仿真等。
11.统计回归分析法：通过建立自变量与因变量之间的关系来分析问题，常用的方法有线性回归、非线性回归等。
12.优化方法：通过求解函数的最大值或最小值来求解问题，常用的方法有迭代法、梯度下降法、遗传算法等。
13.系统动力学方法：通过建立动力学模型来分析系统的演化过程，常用的方法有积分方程、差分方程等。
14.图像处理方法：通过数学模型和算法来处理和分析图像，常用的方法有小波变换、边缘检测等。
15.知识图谱方法：通过构建知识图谱来描述和分析知识之间的关系，常用的方法有图论、语义分析等。
数学建模中的参数拟合方法数学建模是研究实际问题时运用数学方法建立模型，分析和预测问题的一种方法。
在建立模型的过程中，参数拟合是非常重要的一环。
所谓参数拟合，就是通过已知数据来推算模型中的未知参数，使模型更加精准地描述现实情况。
本文将介绍数学建模中常用的参数拟合方法。
一、最小二乘法最小二乘法是一种常用的线性和非线性回归方法。
该方法通过最小化误差的平方和来估计模型参数。
同时该方法的优点在于可以使用简单的数学公式解决问题。
最小二乘法的基本思想可以简单地表示如下：对于给定的数据集合，设其对应的观测值集合为y,$y_1,y_2,...,y_n$，对应的自变量集合为x,$x_1,x_2,...,x_n$，则目标是找到一组系数使得拟合曲线最接近实际数据点。
通常拟合曲线可以用如下所示的线性方程表示：$$f(x)=a_0+a_1x+a_2x^2+...+a_kx^k$$其中，k为拟合曲线的阶数，$a_i$表示第i个系数。
最小二乘法的目标即为找到一组系数${a_0,a_1,...,a_k}$，使得曲线拟合残差平方和最小：$$S=\sum_{i=1}^{n}(y_i-f(x_i))^2$$则称此时求得的拟合数学模型为最小二乘拟合模型。
最小二乘法在实际问题中应用广泛，如线性回归分析、非线性回归分析、多项式拟合、模拟建模等领域。
对于非线性模型，最小二乘法的数学公式比较复杂，需要使用计算机编程实现。
二、梯度下降法梯度下降法是一种优化算法，通过求解函数的导数，从而找到函数的最小值点。
在数学建模中，梯度下降法可以用于非线性回归分析，最小化误差函数。
梯度下降法的基本思想为：在小区间范围内，将函数$f(x)$视为线性的，取其一阶泰勒展开式，在此基础上进行优化。
由于$f(x)$的导数表示$f(x)$函数值增大最快的方向，因此梯度下降法可以通过调整参数的值，逐渐朝向函数的最小值点移动。
具体地，对于给定的数据集合，设其对应的观测值集合为y,$y_1,y_2,...,y_n$，对应的自变量集合为x,$x_1,x_2,...,x_n$，则目标是找到一组系数使得拟合曲线最接近实际数据点。
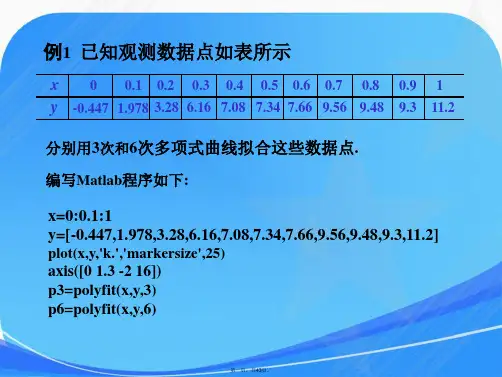
数学建模数据拟合例题解析近年来，数学建模在各个领域得到了广泛的应用，其中数据拟合作为数学建模中重要的一环，更是被广泛应用于实际问题中。
本文将以一个例题为例，通过建模和代码的方法，解析数据拟合的过程，帮助读者更好地理解和应用数据拟合的方法。
1. 问题描述假设我们有一组实验数据，数据中包含了一个变量x和一个变量y，我们想通过这组实验数据，建立一个数学模型来描述x和y之间的关系，并且用这个模型来预测其他x对应的y值。
2. 数据分析我们需要对实验数据进行分析，观察数据的分布规律以及x和y之间的关系。
通常情况下，我们可以通过绘制散点图的方式来直观地观察数据的分布情况。
3. 数据拟合模型的选择在观察了实验数据的分布规律之后，我们需要选择一个适合的数据拟合模型来描述x和y之间的关系。
常用的数据拟合模型包括线性回归模型、多项式拟合模型、指数拟合模型、对数拟合模型等。
在选择模型时，需要考虑模型的复杂程度、拟合效果以及实际问题的需求。
4. 模型建立选择了数据拟合模型之后，我们需要利用实验数据来建立模型，通常可以通过最小二乘法或者最大似然估计的方法来确定模型的参数。
以线性回归模型为例，假设模型为y=ax+b，我们需要通过最小二乘法来确定参数a和b的取值，使得模型能够最好地拟合实验数据。
5. 模型评估建立模型之后，我们需要对模型进行评估，以确定模型的拟合效果。
常用的评估指标包括决定系数R^2、均方误差MSE等。
通过这些评估指标，我们可以了解模型的拟合效果如何，并且对模型进行优化和改进。
6. 模型预测我们可以利用建立的模型来进行预测，预测其他x对应的y值。
通过模型预测，我们可以更好地理解实验数据中x和y之间的关系，从而为实际问题的决策提供支持。
通过以上的解析，我们可以清楚地了解了数据拟合的整个过程，包括数据分析、模型选择、模型建立、模型评估以及模型预测等环节。
通过这些方法和步骤，我们可以更好地理解和应用数据拟合的方法，在实际问题中更好地解决实际问题。
