数学建模方法 拟合

数学模型拟合作业引言数学模型是数学与实际问题相结合的产物，通过建立数学模型能够对复杂的实际问题进行简化和抽象，使其更易于分析和求解。

在现实生活中，我们经常会遇到一些问题需要拟合一个数学模型，以便更好地了解问题的本质和规律。

本文将介绍数学模型拟合的基本概念、常用的拟合方法以及实际应用。

数学模型拟合的基本概念1.1 数学模型数学模型是利用数学语言和符号对实际问题进行抽象和描述的工具。

它可以通过一系列的数学方程来描述问题的属性、关系和行为，从而使问题更易于分析和求解。

数学模型通常包括数学模型的定义、变量的定义、约束条件和目标函数等要素。

1.2 拟合问题在实际问题中，我们通常会根据已知的数据或观测到的现象，试图通过建立一个数学模型来描述数据或现象之间的关系。

这个过程称为拟合，也被称为参数估计或函数逼近。

拟合问题的目标是找到一个数学模型，使得该模型与已知的数据或观测结果的残差最小化。

常用的拟合方法2.1 线性回归线性回归是最常用的拟合方法之一，它假设拟合函数与自变量之间存在一个线性关系。

线性回归问题可以通过最小二乘法来求解，即通过最小化残差平方和来确定拟合函数的参数。

2.2 非线性回归在实际问题中，往往存在非线性关系的情况，因此线性回归并不能完全拟合数据。

为了解决这个问题，可以使用非线性回归方法。

非线性回归方法包括多项式拟合、指数拟合、对数拟合等，通过将非线性函数线性化，再利用线性回归方法进行拟合。

2.3 曲线拟合曲线拟合是一种通过将一条曲线与数据点进行拟合的方法。

曲线拟合通常使用的函数包括多项式函数、指数函数、对数函数、幂函数等。

曲线拟合的目标是找到一条曲线，使得曲线与数据点之间的误差最小化。

2.4 插值拟合插值拟合是一种通过已知数据点之间的插值来拟合的方法。

插值拟合可以通过拉格朗日插值法、牛顿插值法等方法进行。

插值拟合的目标是找到一个函数，使得该函数经过已知的数据点。

实际应用3.1 经济学中的拟合问题在经济学中，拟合问题是非常常见的。

摘要冬青是一种寄生在大树上部树枝的药科植物。

本文主要研究每株大树上冬青的数量与大树年龄之间的关系。

本文主要是运用两种方法，一是线性化模型求解，二是非线性模型求解。

1.线性化求解，由于题目中的数据对参数是非线性的，因此要通过两边取对数的方法转化为线性模型，即εln ln ln ++=bx a y模型中的因变量y ln 对新的参数A 、B 是线性的。

运用MATLAB 进行线性拟合因而得到A 、B 的值，从而得到a 、b 的值从而得到回归方程x b e a yˆˆˆ= 2.非线性模型求解，题目中的数据对参数是非线性的，因此可以用非线性回归的方法直接估计模型中的参数。

模型的求解可以用MATLAB 统计工具箱中的命令进行，使用格式为：[beta,R,J]=nlinfit(x,Y,'f1',beta0)Nlinfit 函数可以对给出的数据进行非线性回归，确定出参数的值，从而得到回归方程x b e a yˆˆˆ= 关键词: 线性回归 非线性回归 nlinfit一．问题重述冬青是一种寄生在大树上部树枝的药科植物，它喜欢寄生在年轻的大树上，以模型Y=εbx ae ,ln ε～N(0,2σ)拟合数据，试求曲线回归方程()x b a yˆex p ˆˆ=。

二．基本假设1.每株大树的生长环境是一样；2.影响大树上冬青寄生的株数的环境因素也是一样。

三．符号说明四．问题分析由数据绘制出散点图如下：以大树的年龄x 为自变量、以每株大树上冬青寄生的株数y 为因变量，利用MATLAB 统计工具箱的plot 命令画出散点图如图1，使用程序见附录程序1图1 散点图下面可以用εbx ae y =拟合数据。

其中ε为随机误差。

这个模型是非线性的，因此要通过两边取对数将其变成线性的，即bx a y ++=εln ln ln 。

可以将其看成是一元线性方程：εln ln ++=Bx A y 。

则y ln 对x 是线性的。

输出b 为a ln 和b 的估计值，bint 为b 的置信区间，stats 为回归模型的检验统计量，分别为回归方程的决定系数2R ,统计量值F ，概率值p 。

数学实验与数学建模实验报告学院：南通大学理学院班级：信计111学号：姓名：实验名称：线性拟合与非线性拟合指导教师：填写日期：2013年11月5日实验五线性拟合与非线性拟合一、实验指导解读本实验的主要目的是了解迭代法，研究迭代数列的收敛性，学习线性方程组的求解以学习非线性方程组的求解。

本次实验是通过两个变量的多组记录数据利用最小二乘法寻求两个变量之间的函数关系。

两个变量之间的函数关系主要有两种：一是线性关系（一次函数）；二是非线性关系（非一次的其它一元函数）。

因此本实验做两件事：一是线性拟合（习题1）；二是非线性拟合（习题2）。

习题2是用多项式函数、指数函数、双曲函数等初等函数以及分段函数拟合。

二、实验基本方法与理论：（习题1）线性拟合修改、补充程序要说明拟合效果，主要从形（大多数散点是否在拟合曲线上或附近）与量（残差是否小）！计算残差的程序：假设对两个变量的多组记录数据已有程序biao={{x1,y1},{x2,y2},…,{xn,yn}}并且通过Fit得到线性拟合函数y=ax+b我们可以先定义函数（程序）f[x_]:=a*x+b再给出计算残差的程序dareta=Sum[(biao[[i ,2]]-f[biao[[i ,1]]])^2,{i ,1, n}]程序说明：biao[[i]]是提取表biao的第i行，即{xi,yi}biao[[i ,1]] 是提取表biao的第i行的第一个数, 即xibiao[[i ,2]] 是提取表biao的第i行的第一个数, 即yibiao[[i ,2]]-f[biao[[i ,1]]] 即yi-(a*xi+b)（习题2）非线性拟合修改、补充程序要说明拟合效果，主要从形（大多数散点是否在拟合曲线上或附近）与量（残差是否小）！计算残差的程序：假设对两个变量的多组记录数据已有程序biao={{x1,y1},{x2,y2},…,{xn,yn}}并且通过Fit得到非线性拟合函数y=f(x)我们可以先定义函数（程序）f[x_]:=再给出计算残差的程序dareta=Sum[(biao[[i ,2]]-f[biao[[i ,1]]])^2,{i ,1, n}]程序说明：biao[[i]]是提取表biao的第i行，即{xi,yi}biao[[i ,1]] 是提取表biao的第i行的第一个数, 即xibiao[[i ,2]] 是提取表biao的第i行的第一个数, 即yibiao[[i ,2]]-f[biao[[i ,1]]] 即yi-f(xi)三、实验的整体思路（1）对数据线性拟合1、先对习题1的十组数据线性拟合，并从形与量看拟合效果；2、对习题1的十组数据中的9组数据线性拟合，并从形与量看拟合效果；3、对习题1的十组数据中的6组数据线性拟合，并从形与量看拟合效果。

数学建模方法大汇总数学建模是数学与实际问题相结合，通过建立数学模型来解决实际问题的一种方法。

在数学建模中，常用的方法有很多种，下面将对常见的数学建模方法进行大汇总。

1.描述性统计法：通过总结、归纳和分析数据来描述现象和问题，常用的统计学方法有平均值、标准差、频率分布等。

2.数据拟合法：通过寻找最佳拟合曲线或函数来描述和预测数据的规律，常用的方法有最小二乘法、非线性优化等。

3.数理统计法：通过样本数据对总体参数进行估计和推断，常用的方法有参数估计、假设检验、方差分析等。

4.线性规划法：建立线性模型，通过线性规划方法求解最优解，常用的方法有单纯形法、对偶理论等。

5.整数规划法：在线性规划的基础上考虑决策变量为整数或约束条件为整数的情况，常用的方法有分支定界法、割平面法等。

6.动态规划法：通过递推关系和最优子结构性质建立动态规划模型，通过计算子问题的最优解来求解原问题的最优解，常用的方法有最短路径算法、最优二叉查找树等。

7.图论方法：通过图的模型来描述和求解问题，常用的方法有最小生成树、最短路径、网络流等。

8.模糊数学法：通过模糊集合和隶属函数来描述问题，常用的方法有模糊综合评价、模糊决策等。

9.随机过程法：通过概率论和随机过程来描述和求解问题，常用的方法有马尔可夫过程、排队论等。

10.模拟仿真法：通过构建系统的数学模型，并使用计算机进行模拟和仿真来分析问题，常用的方法有蒙特卡洛方法、事件驱动仿真等。

11.统计回归分析法：通过建立自变量与因变量之间的关系来分析问题，常用的方法有线性回归、非线性回归等。

12.优化方法：通过求解函数的最大值或最小值来求解问题，常用的方法有迭代法、梯度下降法、遗传算法等。

13.系统动力学方法：通过建立动力学模型来分析系统的演化过程，常用的方法有积分方程、差分方程等。

14.图像处理方法：通过数学模型和算法来处理和分析图像，常用的方法有小波变换、边缘检测等。

15.知识图谱方法：通过构建知识图谱来描述和分析知识之间的关系，常用的方法有图论、语义分析等。

数学建模中的参数拟合方法数学建模是研究实际问题时运用数学方法建立模型，分析和预测问题的一种方法。

在建立模型的过程中，参数拟合是非常重要的一环。

所谓参数拟合，就是通过已知数据来推算模型中的未知参数，使模型更加精准地描述现实情况。

本文将介绍数学建模中常用的参数拟合方法。

一、最小二乘法最小二乘法是一种常用的线性和非线性回归方法。

该方法通过最小化误差的平方和来估计模型参数。

同时该方法的优点在于可以使用简单的数学公式解决问题。

最小二乘法的基本思想可以简单地表示如下：对于给定的数据集合，设其对应的观测值集合为y,$y_1,y_2,...,y_n$，对应的自变量集合为x,$x_1,x_2,...,x_n$，则目标是找到一组系数使得拟合曲线最接近实际数据点。

通常拟合曲线可以用如下所示的线性方程表示：$$f(x)=a_0+a_1x+a_2x^2+...+a_kx^k$$其中，k为拟合曲线的阶数，$a_i$表示第i个系数。

最小二乘法的目标即为找到一组系数${a_0,a_1,...,a_k}$，使得曲线拟合残差平方和最小：$$S=\sum_{i=1}^{n}(y_i-f(x_i))^2$$则称此时求得的拟合数学模型为最小二乘拟合模型。

最小二乘法在实际问题中应用广泛，如线性回归分析、非线性回归分析、多项式拟合、模拟建模等领域。

对于非线性模型，最小二乘法的数学公式比较复杂，需要使用计算机编程实现。

二、梯度下降法梯度下降法是一种优化算法，通过求解函数的导数，从而找到函数的最小值点。

在数学建模中，梯度下降法可以用于非线性回归分析，最小化误差函数。

梯度下降法的基本思想为：在小区间范围内，将函数$f(x)$视为线性的，取其一阶泰勒展开式，在此基础上进行优化。

由于$f(x)$的导数表示$f(x)$函数值增大最快的方向，因此梯度下降法可以通过调整参数的值，逐渐朝向函数的最小值点移动。

具体地，对于给定的数据集合，设其对应的观测值集合为y,$y_1,y_2,...,y_n$，对应的自变量集合为x,$x_1,x_2,...,x_n$，则目标是找到一组系数使得拟合曲线最接近实际数据点。

数学建模数据拟合例题解析近年来，数学建模在各个领域得到了广泛的应用，其中数据拟合作为数学建模中重要的一环，更是被广泛应用于实际问题中。

本文将以一个例题为例，通过建模和代码的方法，解析数据拟合的过程，帮助读者更好地理解和应用数据拟合的方法。

1. 问题描述假设我们有一组实验数据，数据中包含了一个变量x和一个变量y，我们想通过这组实验数据，建立一个数学模型来描述x和y之间的关系，并且用这个模型来预测其他x对应的y值。

2. 数据分析我们需要对实验数据进行分析，观察数据的分布规律以及x和y之间的关系。

通常情况下，我们可以通过绘制散点图的方式来直观地观察数据的分布情况。

3. 数据拟合模型的选择在观察了实验数据的分布规律之后，我们需要选择一个适合的数据拟合模型来描述x和y之间的关系。

常用的数据拟合模型包括线性回归模型、多项式拟合模型、指数拟合模型、对数拟合模型等。

在选择模型时，需要考虑模型的复杂程度、拟合效果以及实际问题的需求。

4. 模型建立选择了数据拟合模型之后，我们需要利用实验数据来建立模型，通常可以通过最小二乘法或者最大似然估计的方法来确定模型的参数。

以线性回归模型为例，假设模型为y=ax+b，我们需要通过最小二乘法来确定参数a和b的取值，使得模型能够最好地拟合实验数据。

5. 模型评估建立模型之后，我们需要对模型进行评估，以确定模型的拟合效果。

常用的评估指标包括决定系数R^2、均方误差MSE等。

通过这些评估指标，我们可以了解模型的拟合效果如何，并且对模型进行优化和改进。

6. 模型预测我们可以利用建立的模型来进行预测，预测其他x对应的y值。

通过模型预测，我们可以更好地理解实验数据中x和y之间的关系，从而为实际问题的决策提供支持。

通过以上的解析，我们可以清楚地了解了数据拟合的整个过程，包括数据分析、模型选择、模型建立、模型评估以及模型预测等环节。

通过这些方法和步骤，我们可以更好地理解和应用数据拟合的方法，在实际问题中更好地解决实际问题。

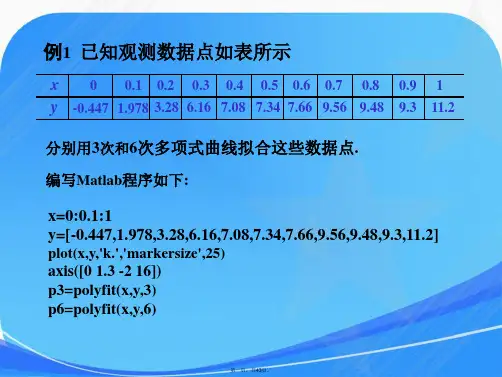
数学建模常见的⼀些⽅法【04拟合算法】@⽬录数学建模常见的⼀些⽅法1. 拟合算法与插值问题不同，在拟合问题中不需要曲线⼀定经过给定的点。

拟合问题的⽬标是寻求⼀个函数（曲线），使得该曲线在某种准则下与所有的数据点最为接近，即曲线拟合的最好（最⼩化损失函数）。

1.1 插值和拟合的区别 插值算法中，得到的多项式f(x)要经过所有样本点。

但是如果样本点太多，那么这个多项式次数过⾼，会造成。

尽管我们可以选择分段的⽅法避免这种现象，但是更多时候我们更倾向于得到⼀个确定的曲线，尽管这条曲线不能经过每⼀个样本点，但只要保证误差⾜够⼩即可，这就是拟合的思想。

(拟合的结果是得到⼀个确定的曲线)1.2 求解最⼩⼆乘法1.3 Matlab求解最⼩⼆乘测试数据:x =4.20005.90002.70003.80003.80005.60006.90003.50003.60002.90004.20006.10005.50006.60002.90003.30005.90006.00005.6000>> yy =8.400011.70004.20006.10007.900010.200013.20006.60006.00004.60008.400012.000010.300013.30004.60006.700010.800011.50009.9000计算代码:>> plot(x,y,'o')>> % 给x和y轴加上标签>> xlabel('x的值')>> ylabel('y的值')>> n = size(x,1);>> k = (n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x))>> b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x))>> hold on % 继续在之前的图形上来画图形>> grid on % 显⽰⽹格线>> f=@(x) k*x+b; % 函数线>> fplot(f,[2.5,7]); % 设置显⽰范围>> legend('样本数据','拟合函数','location','SouthEast')计算过程：>> plot(x,y,'o')>> % 给x和y轴加上标签>> xlabel('x的值')>> ylabel('y的值')>> n = size(x,1);>> n*sum(x.*y)-sum(x)*sum(y)ans = 1.3710e+03>> n*sum(x.*x)-sum(x)*sum(x)ans = 654.4600>> k = (n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x))k = 2.0948>> b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x))b = -1.0548>> hold on>> grid on>> f=@(x) k*x+b;>> fplot(f,[2.5,7]);>> legend('样本数据','拟合函数','location','SouthEast')1.4 如何评价拟合的好坏线性函数是指对参数为线性（线性于参数）在函数中，参数仅以⼀次⽅出现，且不能乘以或除以其他任何的参数，并不能出现参数的复合函数形式。

mathcad指数拟合
指数拟合是一种常见的数学建模方法，用于拟合具有指数函数
关系的数据。

Mathcad是一种流行的工程计算软件，它提供了强大
的数学建模和数据分析工具，包括指数拟合功能。

在Mathcad中进行指数拟合，可以按照以下步骤进行：
1. 输入数据，首先，将需要进行指数拟合的数据输入到Mathcad工作表中。

这些数据可以是实验测量得到的，或者是需要
进行拟合的现有数据。

2. 选择拟合函数，在Mathcad中，选择“Curve Fitting”工具，然后选择指数函数作为拟合函数类型。

指数函数通常表示为y
= a exp(b x)，其中a和b是拟合参数，x是自变量，y是因变量。

3. 进行拟合，在Mathcad中，选择拟合函数后，可以使用拟合
工具对数据进行拟合。

Mathcad会自动计算最优的拟合参数a和b，
以最小化实际数据与拟合曲线之间的残差。

4. 分析拟合结果，完成拟合后，可以对拟合结果进行进一步分
析。

Mathcad通常会提供拟合参数的置信区间、拟合曲线与实际数
据的对比图等信息，以帮助用户评估拟合的质量和可靠性。

5. 应用拟合结果，最后，根据拟合结果可以进行进一步的预测、分析或者其他应用。

拟合结果可以用于预测未来的数据趋势，或者
用于分析数据之间的相关性等。

总之，Mathcad提供了方便易用的指数拟合工具，可以帮助工
程师和科学家对实验数据进行指数函数拟合，并进行进一步的数据
分析和应用。