七年级数学上册 第6章 图形的初步知识 6.9 直线的相交 第1课时 对顶角同步练习(新版)浙教版

6.9 直线的相交第1课时对顶角一、教学目标：知识目标：1.了解相交线、对顶角的概念。

2.理解对顶角相等。

能力目标：经历观察、猜想、说理、交流等过程，进一步发展空间观念和有条理的表达能力.情感目标：在动手实践、自主探索、合作交流中获得成功的体验，建立自信心;感受数学与生活的密切联系，增强用数学的意识.二、教学重难点：重点：对顶角相等这一性质，两条直线互相垂直的概念，画法及表示法。

难点：例2 需利用有关余角、对顶角的性质，且含较多的说理过程。

三、三、教学过程：（一）导入新课在黑板上画两条直线AB，CD相交于点O（如图6-45），形成四个角：∠1，∠2，∠AOD，∠BOC我们把其中相对的一对角∠1和∠2，∠AOD和∠BOC叫做对顶角。

对顶角有以下特点：1.顶点相同，2.角的两边互为反向延长线。

例如：∠1的两边OB，OD分别与∠2的两边OA，OC互为反向延长线。

强调：对顶角是一对角，区别于直角，锐角，钝角这类角的概念。

（二）探究新知例1：如图6-46 三条直线相交于一点O，说出图中的6组对顶角。

分析：关键在于启发学生先找出每一对对顶角的其中一个角。

解：6组对角是：∠FOA与∠EOB，∠AOC与∠BOD，∠COE与∠DOF，∠FOC与∠EOD，∠AOE 与∠BOF，∠COB与∠DOA。

拓展练习： 1. 如图6-45，共有几组对顶角？2. 在图6-45中，若∠1=52°，那么∠2等于多少度？请说明理由。

由第2题的解答可知∠1=∠2。

这是由于∠1与∠2都和∠AOD互补，则∠1=∠2。

一般地，对顶角有下面性质：对顶角相等。

例2：如图6-48，已知：直线AD与BE相交与点O，∠DOE与∠COE互余，∠COE=62°，求∠AOB的度数。

分析方法大致有两种：（1）从已知∠DOE与∠COE互余，∠COE=62°可以先求出∠DOE，又由于∠DOE与∠AOB 是对顶角，所以∠DOE=∠AOB 这样就可以求得∠AOB的度数。

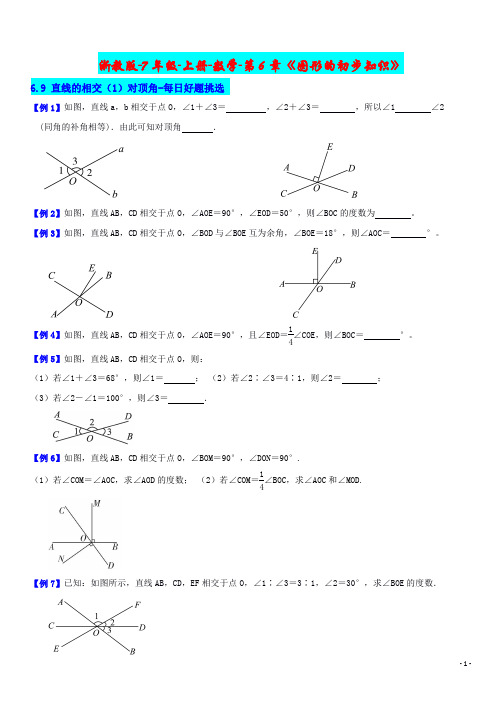
浙教版-7年级-上册-数学-第6章《图形的初步知识》6.9直线的相交（1）对顶角-每日好题挑选【例1】如图，直线a，b 相交于点O，∠1＋∠3＝，∠2＋∠3＝，所以∠1∠2(同角的补角相等)．由此可知对顶角．【例2】如图，直线AB，CD 相交于点O，∠AOE＝90°，∠EOD＝50°，则∠BOC 的度数为。

【例3】如图，直线AB，CD 相交于点O，∠BOD 与∠BOE 互为余角，∠BOE＝18°，则∠AOC＝°。

【例4】如图，直线AB，CD 相交于点O，∠AOE＝90°，且∠EOD＝14∠COE，则∠BOC＝°。

【例5】如图，直线AB，CD 相交于点O，则：（1）若∠1＋∠3＝68°，则∠1＝；（2）若∠2∶∠3＝4∶1，则∠2＝；（3）若∠2－∠1＝100°，则∠3＝．【例6】如图，直线AB，CD 相交于点O，∠BOM＝90°，∠DON＝90°.（1）若∠COM＝∠AOC，求∠AOD 的度数；（2）若∠COM＝14∠BOC，求∠AOC 和∠MOD.【例7】已知：如图所示，直线AB，CD，EF 相交于点O，∠1∶∠3＝3∶1，∠2＝30°，求∠BOE 的度数．【例8】如图，直线AE与CD相交于点B，射线BF平分∠ABC，射线BG在∠ABD内，（1）若∠DBE的补角是它的余角的3倍，求∠FBC的度数；（2）在（1）的件下，若∠DBG＝∠ABG－33°，求∠ABG的度数；（3）若∠FBG＝100°，求∠ABG和∠DBG的度数的差．【例9】如图，已知直线AB与直线CD相交于点O，∠BOE＝90°，OF平分∠BOD，∠BOC∶∠AOC＝1∶3.（1）求∠DOE，∠COF的度数；（2）若射线OF，OE同时绕O点分别以2°/s，4°/s的速度，顺时针匀速旋转，当射线OE，OF的夹角为90°时，两射线同时停止旋转．设旋转时间为t，试求t的值．【例9】观察图，回答下列各题．（1）图①中，共有对对顶角，可以看做＝×；（2）图②中，共有对对顶角，可以看做＝×；（3）图③中，共有对对顶角，可以看做＝×；（4）通过（1）～（3）题中直线条数与对顶角对数之间的关系，说明n(n≥2)条直线相交于一点，可以形成几对对顶角。

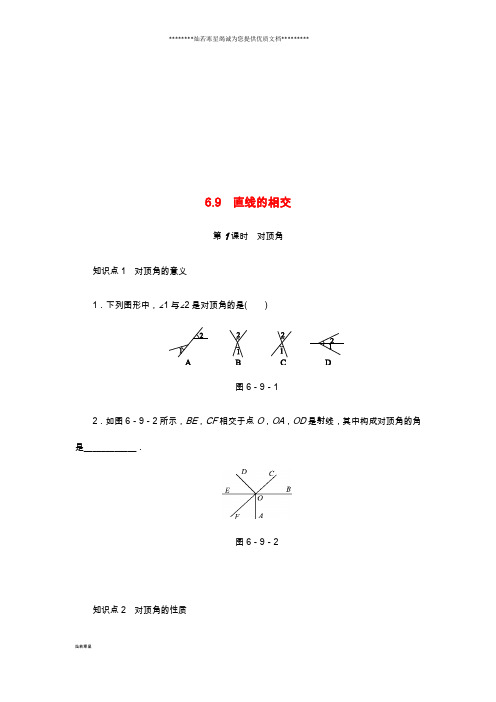
6.9 直线的相交第1课时对顶角知识点1 对顶角的意义1．下列图形中，∠1与∠2是对顶角的是( )图6－9－12．如图6－9－2所示，BE，CF相交于点O，OA，OD是射线，其中构成对顶角的角是____________．图6－9－2知识点2 对顶角的性质3．如图6－9－3，直线a，b相交于点O，∠1＋∠3＝________，∠2＋∠3＝________(邻补角的定义)，所以∠1________∠2(同角的补角相等)．由此可知对顶角________．图6－9－34．已知∠α和∠β是对顶角，∠α＝30°，则∠β的度数为( )A．30°B．60°C．70°D．150°5．如图6－9－4，图中是对顶角量角器，用它测量角的原理是______________.图6－9－46．如图6－9－5，直线AB，CD，EF交于一点O.图6－9－5(1)∠EOB的对顶角是________；(2)________是∠AOE的对顶角；(3)若∠AOC＝76°，则∠BOD的度数为________．7．如图6－9－6所示，直线AB与CD相交于点O，若∠AOC＋∠BOD＝90°，则∠BOC ＝________°.图6－9－68．如图6－9－7所示，∠1＝120°，∠2＋∠3＝180°，则∠4＝________°.图6－9－79. 如图6－9－8，直线AB，CD相交于点O，∠1＝40°，求∠2，∠3，∠4的度数．图6－9－810．如图6－9－9所示，直线AB，CD相交于点O，OE平分∠AOC，∠EOC＝35°，求∠BOD的度数．图6－9－911．如图6－9－10，直线AB，CD，EF相交于点O，∠AOD＝150°，∠EOD＝80°，求∠AOF的度数．图6－9－1012．如图6－9－11，直线AB，CD相交于点O，OE平分∠AOC，OF平分∠DOB，则点E，O，F在同一直线上，请说明理由．(补全解答过程)图6－9－11解：∵直线AB，CD相交于点O，∴∠AOC＝________(对顶角相等)．∵OE平分∠AOC，OF平分∠DOB，∴∠AOE＝______∠AOC，∠BOF＝______∠DOB，∴∠AOE＝________．∵∠AOF＋∠BOF＝∠AOB＝180°，∴∠AOF＋∠AOE＝∠EOF＝180°，∴点E，O，F在同一直线上．13．如图6－9－12，直线AB与CD相交于点O，∠BOE＝∠COF＝90°，且∠BOF＝32°，求∠AOC与∠EOD的度数．图6－9－1214．已知：如图6－9－13所示，直线AB，CD，EF相交于点O，∠1∶∠3＝3∶1，∠2＝30°，求∠BOE的度数．图6－9－1315．观察图6－9－14，回答下列各题．(1)图①中，共有________对对顶角，可以看作________＝________×________；(2)图②中，共有________对对顶角，可以看作________＝________×________；(3)图③中，共有________对对顶角，可以看作________＝________×________；(4)通过(1)～(3)各题中直线条数与对顶角对数之间的关系，若有n(n≥2)条直线相交于一点，则可形成几对对顶角？图6－9－141．C 2.∠EOF和∠BOC，∠COE和∠BOF 3．180°180°＝相等4．A 5.对顶角相等6．(1)∠AOF(2)∠BOF(3)76°7．135 8.609．解：∵∠1＝40°，∠1＝∠2，∴∠2＝40°.∵∠1＝40°，∠1＋∠3＝180°，∴∠3＝140°.又∵∠3＝∠4，∴∠4＝140°.10. 解：∵OE平分∠AOC，∠EOC＝35°，∴∠AOC＝2∠EOC＝35°×2＝70°.由对顶角相等可知：∠BOD＝∠AOC＝70°. 11．解：∵∠AOD＝150°，∠AOD＋∠BOD＝180°，∴∠BOD＝30°.又∵∠EOD＝80°，∴∠EOB＝80°－30°＝50°，∴∠AOF＝∠EOB＝50°.12．∠DOB 1212∠BOF13．解：∵∠COF＝90°，∠BOF＝32°，∴∠COB＝90°－32°＝58°＝∠AOD.∵∠BOE＝90°，∴∠EOA＝180°－90°＝90°，∠EOC＝90°－∠COB＝32°，∴∠AOC＝∠EOA＋∠EOC＝122°，∠EOD＝∠EOA＋∠AOD＝148°.14．解：∵∠1＋∠2＋∠3＝180°，且∠1∶∠3＝3∶1，∠2＝30°，∴∠1＝112.5°，∠3＝37.5°，∴∠BOE＝∠1＝112.5°.15．解：(1)共有2对对顶角，可以看作2＝2×1.(2)单个角是对顶角的有3对，两个角组成复合角的对顶角有3对，共有6对，可以看作6＝3×2.(3)单个角是对顶角的有4对，两个角组成复合角的对顶角有4对，三个角组成复合角的对顶角有4对，共有12对，可以看作12＝4×3.(4)n(n≥2)条直线相交于一点，可形成n(n－1)对对顶角．。

6.9 直线的相交第1课时对顶角一、教学目标：知识目标：1.了解相交线、对顶角的概念。

2.理解对顶角相等。

能力目标：经历观察、猜想、说理、交流等过程，进一步发展空间观念和有条理的表达能力.情感目标：在动手实践、自主探索、合作交流中获得成功的体验，建立自信心;感受数学与生活的密切联系，增强用数学的意识.二、教学重难点：重点：对顶角相等这一性质，两条直线互相垂直的概念，画法及表示法。

难点：例2 需利用有关余角、对顶角的性质，且含较多的说理过程。

三、三、教学过程：（一）导入新课在黑板上画两条直线AB，CD相交于点O（如图6-45），形成四个角：∠1，∠2，∠AOD，∠BOC我们把其中相对的一对角∠1和∠2，∠AOD和∠BOC叫做对顶角。

对顶角有以下特点：1.顶点相同，2.角的两边互为反向延长线。

例如：∠1的两边OB，OD分别与∠2的两边OA，OC互为反向延长线。

强调：对顶角是一对角，区别于直角，锐角，钝角这类角的概念。

（二）探究新知例1：如图6-46 三条直线相交于一点O，说出图中的6组对顶角。

分析：关键在于启发学生先找出每一对对顶角的其中一个角。

解：6组对角是：∠FOA与∠EOB，∠AOC与∠BOD，∠COE与∠DOF，∠FOC与∠EOD，∠AOE 与∠BOF，∠COB与∠DOA。

拓展练习： 1. 如图6-45，共有几组对顶角？2. 在图6-45中，若∠1=52°，那么∠2等于多少度？请说明理由。

由第2题的解答可知∠1=∠2。

这是由于∠1与∠2都和∠AOD互补，则∠1=∠2。

一般地，对顶角有下面性质：对顶角相等。

例2：如图6-48，已知：直线AD与BE相交与点O，∠DOE与∠COE互余，∠COE=62°，求∠AOB的度数。

分析方法大致有两种：（1）从已知∠DOE与∠COE互余，∠COE=62°可以先求出∠DOE，又由于∠DOE与∠AOB 是对顶角，所以∠DOE=∠AOB 这样就可以求得∠AOB的度数。

浙江版2019－2020学年度七年级数学上册第6章6.9直线的相交第1课时 直线的相交(1)【知识清单】1. 两条直线相交:如果两条直线只有一个公共点，就说这两条直线相交.该公共点叫做这两条直线的交点.2. 对顶角:顶点相同且一个角的两边是另一个角两边的反向延长线的两个角叫对顶角.3.对顶角的性质：对顶角相等. 【经典例题】例题1、下列图中，∠1与∠2是对顶角的是( )【考点】对顶角、邻补角．【分析】根据对顶角的定义进行逐个判定即可.对顶角定义含两层意思；一是有相同的顶点；二是一个角的两边是另一个角两边的反向延长线，二者缺一不可.【解答】A 、顶点相同，但一个角的两边不是另一个角两边的反向延长线，结论错误； B 、顶点相不同，结论错误；C 、顶点相同，但一个角的两边不是另一个角两边的反向延长线，结论错误；D 、符合定义，结论正确． 故选D.【点评】本题主要考查了对顶角的定义，熟记对顶角定义和相关图形是解题的关键． 例题2、如图，直线AB ，CD ，EF 相交于点O ，则∠1+∠2+∠3的度数为 . 【考点】对顶角相等．【分析】根据对顶角相等求出∠3=∠COB ，再根据平角定义解答． 【解答】如图：∵直线AB ，CD ，EF 相交于点O ， ∴∠3=∠COB ， ∴∠1+∠2+∠3=∠1+∠COB +∠2 =180°.故答案为：180°．【点评】本题考查了对顶角相等的性质，把三个角转化为一个平角是解题的关键． 【夯实基础】1．如图，直线AB ，CD 相交于点O .若∠3=110°，则∠1的度数为( )A. B. C D 例题2图A ．15°B ．25°C ．35°D ．70°2． 如图，OA 是北偏西46°38′方向的一条射线，射线OD 是射线OB 的反向延长线，若∠AOB =90°， 则OD 的方向是( )A ．北偏西43°22′B ．西偏南43°22′C ．南偏西43°22′D ．北偏东43°22′3．∠1的对顶角是∠2，∠2的补角是∠3.若∠3=55°，则∠1的度数是( ) A ．45° B ．55° C ．55°或125° D ．125°4．如图，直线EF 与直线AB 、CD 分别相交于点E 、F .若∠1＋∠2=180°，则图中与∠1相等 的角(不含∠1)有( )A ．4个B ．3个C ．2个D ．1个5．(1)如图是一个对顶角量角器，用它测量角的原理是____________．(2)如图，直线AB 和CD 相交于点O ，OE 平分∠AOB ，∠AOD =130°，则∠COE 的度数 是 度．6．下列论断：①有公共顶点的两个角是对顶角；②有公共顶点且一个角的两边是另一个角两边 的反向延长线的两个角是对顶角；③不是对顶角的两个角一定不相等；④对顶角相等；⑤相 等的两个角是对顶角.其中正确的结论是 (填序号). 7 . 动手在同一平面内有12条直线，最少把平面分成几部分？最多分成几部分？8．如图，直线AB ，CD 相交于点O ，OF 平分∠AOB ，OB 平分∠DOE ，若∠FOE =50°，求∠AOC的度数．第1题图第2题图第5题图(1)第5题图(2)第4题图第8题图9.如图，直线AB 与CD 相交于点O ，OE 平分∠AOD ，(1) 若∠AOC :∠AOD =1:2，①求∠EOB 的度数；②与∠AOC 相等的角有几个？ 把它们写出来.(2) 若∠AOC =2α，求∠EOD 的度数.【提优特训】10．如图，直线AB 与CD 相交于点O ，若∠1＋∠2=76°，则∠3等于( )A ．104°B ．122°C ．132°D ．142°11．10条直线两两相交，交点最多为a 个，交点最少为b 个，则a +b 的值为( )A ．11B ．23C ．31D ．4612．如图，图中的直线表示原有的公路，计划在AB 两城市之间沿直线再建一条公路，这条公路与原有公路之间的交叉处都需建一座公路立交桥，则要建的公路立交桥的总数为( ) A ．4座 B ．5座 C ．6座 D ．7座13.平面上三条直线，它们的交点个数可能是()个A ．0或1或2B ．0或1或3C ． 1或3D ．0或1或2或3 14．n 条直线两两相交，当交点个数最多时，其对顶角共有 组15．如图，有两堵围墙，有人想测量地面上两堵围墙内所形成的∠AOB 的度数，但人又不能进 入围墙，只能站在墙外，请问该如何测量? 16．(1)阅读理解，并回答问题：①如图(1)中有 组对顶角； ②如图(2)中有 组对顶角； ③如图(3)中有 组对顶角； (2)依据上述的规律，解得下列问题：① 10条直线相交于点O ，图中共有多少组对顶角?第9题图第10题图第15题图第12题图② n 条直线相交于点O ，图中共有多少组对顶角? ③ 2019条直线相交于点O ，图中共有多少组对顶角?17.如图，直线AB ，CD 相交于点O ，OC平分∠AOE ，OF 在∠EOB 的内部， ∠EOF =21∠FOB ，∠COF =70°．求∠COE 和∠FOD 的度数．18．如图，已知直线AB ，CD 相交于点O ，OE 是∠AOB 的平分线，OB 平分∠DOF ，若∠EOC =∠EOD + 120°，求∠3与∠4的度数，并判定∠3与∠4的大小关系？19．如图，直线AB 、CD 、EF 相交于点O .(1)若∠1=21°，∠2=32°，求∠3的度数； (2) 若9∠2=2∠3，∠1=26°，求∠AOF 的度数； (3) 若∠3－∠2=96°，∠1=20°，求∠EOB 的度数；20． 以此类推总结规律，解决下列问题：n 条直线相交最多有几个交点？ 2019条直线相交最多有几个交点？第20题图(1) 第20题图(2) 第20题图(3)第16题图(1) 第16题图(2) 第16题图(3) 第17题图第18题图第19题图【中考链接】21．(2019•模拟) 如图，直线AB ，CD ，EF 相交于点O ，OG 是∠AOF 的平分线，∠BOD =35°，∠COE =19°，则∠COG 的度数是________．22．(2019•模拟)如图，直线AB ，CD 相交于点O ，∠EOC =70°，OA平分∠EOC ，求∠BOD 的度数．第21题图第22题图参考答案1、C2、C3、B4、D5、(1)对顶角相等 (2)406、②④ 10、D 11、D 12、B 13、D 14、n (n －1) 21、98°7 . 解：(1)有一条直线时，最少分成2部分，最多分成1+1=2部分； (2)有两条直线时，最少分成4部分，最多分成1+1+2=4部分； (3)有三条直线时，最少分成6部分，最多分成1+1+2+3=7部分；(4)设直线条数有n 条，分成的平面最多有a 个，最少有b 个，有以下规律：8．解：∵AB 为直线，OF 平分∠AOB ，∴∠AOF =∠BOF =90°. ∵∠FOE =50°，∴∠EOB =∠BOF －∠FOE =40°. ∵OB 平分∠DOE ，∴∠AOC =∠DOB =∠BOE =40°.9. 解：(1)∵①∠AOC :∠AOD =1:2，∠COD =180°.∴∠AOC . ∴∠AOD =2∠AOC =120°. ∴∠DOB =∠AOC =60°.∵OE 平分∠AOD ， ∴∠EOD . ∴∠EOB =∠EOD +∠DOB =120°.②∠AOC 相等的角有∠AOE 、∠EOD 、∠DOB. (2) ∠AOC =2α，第8题图第9题图∠AOD =∠COD －∠AOC =180°－2α. ∵OE 平分∠AOD ， ∴∠EOD－α. 15． 解：(1)只要延长BO (或AO )至C ，测出∠AOB 的邻补角∠AOC (或∠BOC ) 的大小后，就可知道∠AOB 的度数. (2)反向延长OA 、OB 得到射线OE 、OF ，则∠EOF 是∠AOB 的对顶角，测出 ∠EOF 的大小，就可知道∠AOB 的度数.16.解：(1) ①如图(1)中有 2 组对顶角；②如图(2)中有 2+3=5 组对顶角； ③如图(3)中有 2+3+4=9 组对顶角.(2) ①2+3+4+5+6+7+8+9+10=1+2+3+4+5+6+7+8+9+10－1=1210)101(-⨯+=54组对顶角； ②2+3+…+n －1+n =(1+2+3+…+n －1+n )－1 =12)1(-⨯+nn ； ③122019)20191(-⨯+=2039189.17. 解：设∠3=x °， ∵∠COF =70°．∴∠2=∠COF －∠3=(70－x )°. ∵∠EOF =21∠FOB ， ∴∠FOB=2∠EOF =2∠3=2x °.∵OC 平分∠AOE ， ∴∠1=∠2=(70－x )°. ∵AB 的直线， ∴∠AOB =180°.∴∠1+∠2+∠3+∠FOB =180°. 70－x +70－x +x +2x =180 解得x =40°，2x =80°. ∴∠COE =∠2=(70－40)°=30°.第15题图第17题图∴∠FOD =∠FOB+∠4=∠FOB+∠1=80°+30°=110°. 18．解：∵CD 是直线，∴∠COD =∠EOC +∠EOD =180°. ∵∠EOC =∠EOD + 120°， ∴∠EOD + 120°+∠EOD =180°. 解得∠EOD =30°，∴∠EOC =∠EOD + 120°=30°+120°=150°. ∵OE 是∠AOB 的平分线，∠AOB =180° ∴∠AOE =∠EOB =21∠AOB =90°. ∴∠1=∠EOC －∠AOE =150°－90°=60°. ∵∠1与∠2是对顶角， ∴∠1=∠2=60°. ∵OB 平分∠DOF ， ∴∠3=∠2=60°.∴∠4=∠AOB －∠1－∠3=60°. ∴∠3=∠4.19．解：(1)∵直线AB 、CD 、EF 相交于点O . ∴∠1=∠DOF =21°，∠2=∠AOE =32°， ∵∠AOE +∠3+∠DOF =180°， ∴∠3=127°. (2)设∠2=x °，则∠°， ∵∠AOE +∠3+∠DOF =180°， ∴∠2+∠3+∠1=180°， 即：x x +26=180. 解得x =28°°=126°. ∴∠2=28°，∠3=126°.∴∠AOF =∠AOD +∠DOF =∠3+∠1=152°. (3)设∠2=x °，则∠3=x °+96°， ∵∠AOE +∠3+∠DOF =180°， ∴∠2+∠3+∠1=180°， 即：x + x+96+20=180.第18题图第19题图解得x =32°，x °+96°=128°. ∴∠2=32°，∠3=128°.∴∠EOB =∠1+∠COB =∠1+∠3=20°+128°=148°.20．解(1) 1，(2)3=1+2，(3)6=1+2+3，的度数．解：∵OA 平分∠EOC ，∠EOC =70°， ∴∠AOC =21∠EOC =35°， ∴∠BOD =∠AOC =35°.第22题图。