【三轮冲刺】2015年高考数学《100天冲刺每日一练-必有一得》第98天(含精析)
- 格式:doc
- 大小:374.50 KB
- 文档页数:5

100天冲刺 第 79天一、选择题。
1.已知数列}{n a 的前n 项和为)34()1(2117139511--++-+-+-=+n S n n ,则312215S S S -+的值是A .-76B .76C .46D .132.若集合A ={x||x|>1,x ∈R},B ={y|y =2x 2,x ∈R},则(∁R A )∩B =( ).A .{x|-1≤x ≤1}B .{x|x ≥0}C .{x|0≤x ≤1}D .∅3.已知角θ的顶点与原点重合,始边与横轴的正半轴重合,终边在直线2y x =上,则cos2θ=A .一35B .-45C .23D .344.已知向量()3,4a =,若5λ=a ,则实数λ的值为( ) A .15 B .1 C .15± D .1± 5.已知数列{}n a 的通项公式2133134n a n n =-+-. 当12323434512n n n a a a a a a a a a a a a +++++⋅⋅⋅+取得最大值时,n 的值为( )A .7B .8C .9D .106.函数()lg |sin |f x x =是( ).A .最小正周期为π的奇函数B .最小正周期为2π的奇函数C .最小正周期为π的偶函数D .最小正周期为2π的偶函数7.已知x ,y ,z ∈R +且x+y+z=1则x 2+y 2+z 2的最小值是( ) A.1 B. C. D.2 8.设i 时虚数单位,若复数imi +-12为纯虚数,则实数m 的值为( ) A.2 B.2- C.21 D.21-二、填空题。
9.对任意的0x >,总有 ()|lg |0f x a x x =--≤,则a 的取值范围是 .10.已知向量,a b 满足2,a b a b ==+= a 与b 夹角的余弦值为 .三、解答题。
11.(本题满分12分)在等差数列{}n a 中,138a a +=,且4a 为2a 和9a 的等比中项,求数列{}n a 的首项、公差及前n 项和.12.如图,四棱锥P-ABCD 中,底面ABCD 为正方形,DA ⊥面ABP,AB=1,PA=2,∠PAB=600,E 为PA的中点,F 为PC 上不同于P 、C 的任意一点.(1)求证:PC ∥面EBD(2)求异面直线AC 与PB 间的距离(3)求三棱锥E-BDF 的体积.参考答案1.A【解析】由题可知,此数列先奇偶项分别求和。

100天冲刺 第 84 天一、选择题。
1.已知,,a b c R ∈,命题“若3a b c ++=,则2223a b c ++≥”的否命题是( ) A.若22233a b c a b c ++≠++<,则 B.若22233a b c a b c ++=++<,则 C.若22233a b c a b c ++≠++≥,则D.若22233a b c a b c ++≥++=,则2.设函数(2),2()1()1,22x a x x f x x -≥⎧⎪=⎨-<⎪⎩是R 上的单调递减函数,则实数a 的取值范围为( )A.(,2)-∞B.13(,]8-∞ C.(0,2) D.13[,2)83.设向量,满足|+|=,||=1,||=2,则•等于( )A .B .C .D .4.已知函数()()()()21020x ax x f x a e x ⎧+≥⎪=⎨-<⎪⎩是R 上的单调函数,则实数a 的取值范围是( ) A .()2,+∞ B .(]2,3 C .(],3-∞ D .()2,3 5.在等差数列{}n a 中,9a =12162a +,则数列{}n a 的前11项和11S =( ) A .24 B .48 C .66 D .132 6.下列结论正确的是( ) A .当0>x 且1≠x 时,xx lg 1lg +≥2 B .当0>x 时,xx 1+≥2C .当x ≥2时,xx 1+的最小值为2 D .当x <0≤2时,xx 1-无最大值7.圆222210x y x y +--+=上的点到直线2x y -=的距离最大值是( )1+ D. 1+8.设( )A.都大于2B.至少有一个大于2C.至少有一个不小于2D.至少有一个不大于2二、填空题。
9.如图,点1P ,2P , ,10P 分别是四面体的顶点或其棱的中点,则在同一平面内的四点组()kjiP P P P ,,,1(101≤<<<k j i )共有 个.10.如图,在等腰直角三角形ABC 中,斜边BC =过点A 作BC 的垂线,垂足为1A ;过点1A 作AC 的垂线,垂足为2A ;过点2A 作1AC 的垂线,垂足为3A;…,以此类推,设1BA a =,12AA a =,123A A a =,…,567A A a =,则7a =________.三、解答题。

【三轮冲刺】全国2015届高考数学《100天冲刺每日一练-必有高三一得》第87天一、选择题。
1.若集合P ={-2, 0, 2},i 是虚数单位,则( )A .2i ∈PB .2i ∈PC .(2i)2∈PD .32i∈P 2.下列图形中可以表示以M ={x|0≤x ≤1}为定义域,以N ={y|0≤y ≤1}为值域的函数的图象是( )3.已知角α的终边与单位圆221x y +=交于点01,cos 22P y α⎛⎫ ⎪⎝⎭,则等于( ) A.12- B.12 C.32- D.1 4.已知函数1(0)()1(0)x x f x x x -+<⎧=⎨-≥⎩,解不等式(1)(1)1x x f x ++⋅+≤的解集为( )A .[1,21]--B .(,1]-∞C .(,21]-∞-D .[21,21]--- 5.【原创】已知函数3()sin(2)()2f x x x π=+∈R ,下面结论错误..的是( ) A .函数()f x 的最小正周期为πB .函数()f x 是偶函数C .函数()f x 的图象关于直线4x π=对称 D .函数)(x f 在区间[0,]2π上是增函数6.设{}n a 是等比数列,*m n s t N ∈、、、,则“m n s t +=+”是“m n s t a a a a ⋅=⋅”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7.设,,,A B C D 是空间不共面的四点,且满足0,0,0AB AC AC AD AB AD ⋅=⋅=⋅=,则BCD ∆是( )A .钝角三角形B .锐角三角形C .直角三角形D .不确定8.设O 是正三棱锥P-ABC 底面是三角形ABC 的中心,过O 的动平面与PC 交于S ,与PA 、PB 的延长线分别交于Q 、R ,则和式PSPR PQ 111++( ) A .有最大值而无最小值 B .有最小值而无最大值C .既有最大值又有最小值,两者不等D .是一个与面QPS 无关的常数二、填空题。
100天冲刺 第 83 天一、选择题。
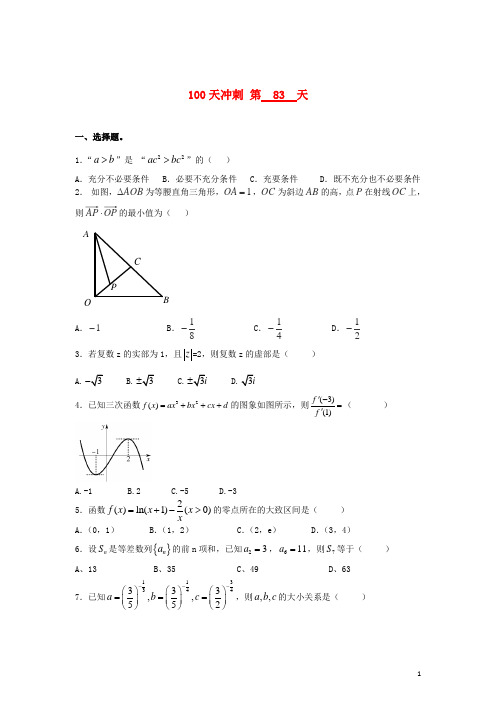
1.“a b >”是 “22ac bc >”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 2. 如图,AOB ∆为等腰直角三角形,1=OA ,OC 为斜边AB 的高,点P 在射线OC 上,则OP AP ⋅的最小值为( )A .1-B .81-C .41-D .21-3.若复数z 的实部为1,且z =2,则复数z 的虚部是( )A.4.已知三次函数32()f x ax bx cx d =+++的图象如图所示,则(3)(1)f f '-='( )A.-1B.2C.-5D.-3 5.函数2()ln(1)(0)f x x x x=+->的零点所在的大致区间是( ) A .(0,1) B .(1,2) C .(2,e ) D .(3,4)6.设n S 是等差数列{}n a 的前n 项和,已知23a =,611a =,则7S 等于( ) A 、13 B 、35 C 、49 D 、63 7.已知113344333,,552a b c ---⎛⎫⎛⎫⎛⎫=== ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,则,,a b c 的大小关系是( ) AOC BP(A).c a b << (B)a b c << (C)b a c << (D)c b a <<8.一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积...为( )A .π12B .π34C .π3D .π312二、填空题。
9.设等差数列{}n a 的公差0d ≠,14a d =,若k a 是1a 与2k a 的等比中项,则k 的值为 .10.定义:如果函数)(x f y =在定义域内给定区间],[b a 上存在0x )(0b x a <<,满足ab a f b f x f --=)()()(0,则称函数)(x f y =是],[b a 上的“平均值函数”,0x 是它的一个均值点,例如2x y =是]1,1[-上的平均值函数,0就是它的均值点.现有函数mx x x f +=3)(是]1,1[-上的平均值函数,则实数m 的取值范围是 .三、解答题。

100天冲刺 第 85 天一、选择题。
1.设1≥>b a ,集合{}a x Z x x A <<∈=0 , |,{}b x b Z x x B <<-∈= , |,记“从集合A 中任取一个元素x ,B x ∉”为事件M ,“从集合A 中任取一个元素x ,B x ∈”为事件N .给定下列三个命题: ①当5=a ,3=b 时,21)()(==N P M P ; ②若1)(=M P ,则2=a ,1=b ; ③1)()(=+N P M P 恒成立.其中,为真命题的是 ( )A .①②B .①③C .②③D .①②③2.设A ,B 为两个不相等的集合,条件()p x A B ∉⋂:, 条件()q x A B ∉⋃:,则p 是q 的( )(A )充分不必要条件 (B )充要条件(C )必要不充分条件 (D )既不充分也不必要条件3.函数()20.4–34y log x x =++的值域是( )(A )(0,–2] (B )[–2,+∞) (C )(–∞,–2] (D )[2,+∞) 4.定义行列式运算1234a a a a =3241a a a a -.将函数sin 2()cos 2x f x x=6π个单位,以下是所得函数图象的一个对称中心是( ) A .,04π⎛⎫⎪⎝⎭B .,02π⎛⎫ ⎪⎝⎭ C .,03π⎛⎫ ⎪⎝⎭ D .,012π⎛⎫⎪⎝⎭ 5.在△ABC 中,已知||4,||1AB AC ==,ABC S ∆=,则AB AC ⋅的值为( ) (A )2-(B )2(C )4±(D )2±6.在递增的等比数列{}n a 中,已知134n a a +=,3264n a a -⋅=,且前n 项和为42n S =,则n =( )(A )3 (B )4 (C )5 (D )67.已知函数3221()13f x x ax b x =+++,若a 是从1,2,3三个数中任取的一个数,b 是从0,1,2三个数中任取的一个数,则该函数有两个极值点的概率为( ) (A )79(B )13(C )59(D )238.已知双曲线22–100ax by a b =(>,>)的一条渐近线方程是0x =,它的一个焦点在抛物线2–4y x =的准线上,则双曲线的方程为( ) (A )4x 2–12y 2=1 (B )4x 2–34y 2=1 (C )12x 2–4y 2=1 (D )3422–41x y =二、填空题。

2013高考百天仿真冲刺卷 数 学(理) 试 卷第Ⅰ卷(选择题 共分) 一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求 的一项. 1.已知全集,,,则 A. B. C. D. 2.复数 A.B.C.D.3.已知等比数列2,且的值为 A.10B.15C.20D.254.如图是一正方体被过棱的中点M、N和顶点A、D、C1截去两个角后所得的几何体,则该几何体的主视图为A. B. C. D.5.若=(12,-3),=(2a-1a2-), 则“a=1”是“”的 A.充分不必要条件B.必要不充分条件 C.充要条件D.既不充分也不必要6.右图是计算函数的值的程序框图,则在①、②、③处应分别填入的是A.,, B.,, C.,, D.,, 7.,动点在直线 上运动,当线段最短时,动点的极坐标是 A. B. C. D.8.已知三棱锥,两两垂直且长度均为6,长为2的线段的一个端点在棱上运动,另一个端点在内运动(含边界),则的中点的轨迹与三棱锥的面所围成的几何体的体积为 A.B.或 C. D.或 第Ⅱ卷(非选择题 共110分) 二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上. 9.的否定是 . 10.函数的 ;单调减区间为 . 11.如图是甲、乙两班同学身高(单位:cm)数据的茎叶图,则甲班同学身高的中位数为 ; 若从乙班身高不低170cm的同学中随机抽取两名,则身高为173cm的同学被抽中的概率为 .甲班 乙班 2 18 1 9 9 1 0 17 0 3 6 8 9 8 8 3 2 16 2 5 8 8 15 9 12.已知是圆的切线,切点为,.是圆的直径,与圆交于点,, 则圆的半径 . 13.已知抛物线双曲线有相同的焦点,点是两曲线的交点,且⊥轴,则双曲线的离心率为 .14.在某条件下的汽车测试中,驾驶员在一次加满油后的连续行驶过程中从汽车仪表盘得到如下信息: 时间油耗(升/100公里)可继续行驶距离(公里)10:009.530011:009.6220注:,, . 从以上信息可以推断在10:00—11:00这一小时内 (填上所有正确判断的序号). 行驶了80公里; 行驶不足80公里; 平均油耗超过9.6升/100公里; 平均油耗恰为9.6升/100公里; 平均车速超过80公里/小时. 三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题满分13分)在中,为角所对的三边,已知. (Ⅰ)求角的值;(Ⅱ)若,,求的长.16.(本小题满分14分) 如图,四棱锥的底面为正方形,侧棱底面,且,分别是线段的中点. (Ⅰ)求证://平面; (Ⅱ)求证:平面; (Ⅲ)求二面角的大小. 17.(本小题满分13分) 为了参加广州亚运会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源人数如下表:队别北京上海天津八一人数4635(Ⅰ)从这18名队员中随机选出两名,求两人来自同一支队的概率; (Ⅱ)中国女排奋力拼搏,战胜韩国队获得冠军.若要求选出两位队员代表发言,设其中来自北京队的人数为,求随机变量的分布列及数学期望.18.(本题满分13分) 已知函数(,实数,为常数). (Ⅰ)若,求在处的切线方程; (Ⅱ)若,讨论函数的单调性.19.(本小题满分14分) 已知点是离心率为的椭圆:上的一点.斜率为直线交椭圆于、两点,且、、三点不. (Ⅰ)求椭圆的方程; (Ⅱ)面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由? (Ⅲ)求证:直线、的斜率之和为定值. 20.(本小题满分13分) 已知集合其中,表示和中所有不同值的个数. 集合,分别求; 若集合,求证:; 是否存在最值?若存在,求出这个最值;若不存在,请说明理由?12345678答案 CCABABBD 二、填空题:本大题共 6 小题,每小题 5 分,共 30 分. 9. , 10. ; 11. 169; 12. 13. 14. ② ③ 三、解答题:本大题共 6 小题,共 80 分. 15.(本小题满分13分) 在中,为角所对的三边,已知. (Ⅰ)求角的值; (Ⅱ)若,,求的长. 解:(Ⅰ) , 分 ---------------------------------------------------------6分 (Ⅱ)在中,, , 分 由正弦定理知: .分 分 16.(本小题满分14分) 如图,四棱锥的底面为正方形,侧棱底面,且,分别是线段的中点. (Ⅰ)求证://平面; (Ⅱ)求证:平面; (Ⅲ)求二面角的大小. 解:建立如图所示的空间直角坐标系, , ,,,.分(Ⅰ)证明:∵,, ∴, ∵平面,且平面, ∴ //平面.5分 (Ⅱ)解:,, , , 又, 平面. 9分 (Ⅲ)设平面的法向量为, 因为,, 则取 又因为平面的法向量为 所以 12分 所以二面角的大小为.14分 17.(本小题满分13分) 为了参加广州亚运会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源人数如下表: 队别北京上海天津八一人数4635(Ⅰ)从这18名队员中随机选出两名,求两人来自同一支队的概率; (Ⅱ)中国女排奋力拼搏,战胜韩国队获得冠军.若要求选出两位队员代表发言,设其中来自北京队的人数为,求随机变量的分布列及数学期望. 解:(Ⅰ)“从这18名队员中随机选出两名,两人来自于同一队”记作事件A, 则. 分 (Ⅱ)的所有可能取值为0,1,2.分 ∵,,, ∴的分布列为: 012P 10分 ∴. 分 18.(本题满分13分) 已知函数(,实数,为常数). (Ⅰ)若,求在处的切线方程; (Ⅱ)若,讨论函数的单调性. 解:(Ⅰ)因为,所以函数, 又,分 所以 即在处的切线方程为---------------------5分 (Ⅱ)因为,所以,则 令,得,.分 (1)当,即时,函数的单调递减区间为,单调递增区间为;分 (2)当,即时,,的变化情况如下表: 所以,函数的单调递增区间为,,单调递减区间为;分 (3)当,即时,函数的单调递增区间为;10分 (4)当,即时,,的变化情况如下表: 所以函数的单调递增区间为,,单调递减区间为;12分 综上,当时,函数的单调递减区间为,单调递增区间为;当时,函数的单调递增区间为,,单调递减区间为;当时,函数的单调递增区间为;当时,函数的单调递增区间为,,单调递减区间为.13分19.(本小题满分14分) 已知点是离心率为的椭圆:上的一点.斜率为直线交椭圆于、两点,且、、三点不. (Ⅰ)求椭圆的方程; (Ⅱ)面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由? (Ⅲ)求证:直线、的斜率之和为定值. 解:(Ⅰ), , ,, ----------------------------------------------5分 (Ⅱ)设直线BD方程为 ----① -----② , 设为点到直线BD的距离, ,当且仅当,时,的面积最大,最大值为--------10分 (Ⅲ)设,直线、的斜率 、,则=------* 将(Ⅱ)中①、②式代入*式整理得=0,即0--------------------------------------14分 20.(本小题满分13分) 已知集合其中,表示和中所有不同值的个数. 集合,分别求; 若集合,求证:; 是否存在最值?若存在,求出这个最值;若不存在,请说明理由?解:(Ⅰ)由 得. 由 得.----------------------------------------------5分 最多有个值,所以 又集合, 任取 当时,不妨设,则, 即. 当时,. 因此,当且仅当时, . 即所有的值两两不同, 所以 -----------------------------------------------9分 (Ⅲ) 存在最值最小值为.可得 所以中至少有个不同的数,即 事实上,设成等差数列, 考虑,根据等差数列的性质, 当时,; 当时,; 因此每个和等于中的一个,或者等于中的一个. 所以对这样的,所以的最小值为. --------------13分 A B D O Y X 是。
专题限时集训(一)A[第1讲 集合与常用逻辑用语](时间:10分钟+25分钟)2012二轮精品提分必练1.已知集合A ={-1,0,a },B ={x |0<x <1},若A ∩B ≠∅,则实数a 的取值范围是( )A .{1}B .(-∞,0)C .(1,+∞)D .(0,1)2.已知M ,N 为集合I 的非空真子集,且M ,N 不相等,若N ∩∁I M =∅,则M ∪N =() A .M B .NC .ID .∅3.设x ,y ∈R ,则“x ≥2且y ≥2”是“x 2+y 2≥4”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件4.已知命题p :∃n ∈N,2n >1000,则綈p 为( )A .∀n ∈N,2n ≤1000B .∀n ∈N,2n >1000C .∃n ∈N,2n ≤1000D .∃n ∈N,2n <10002012二轮精品提分必练1.设集合M ={-1,0,1},N ={a ,a 2},则使M ∩N =N 成立的a 的值是( )A .1B .0C .-1D .1或-12.已知全集U =R ,集合A ={x |lg x ≤0},B ={x |2x ≤1},则∁U (A ∪B )=( )A .(-∞,1)B .(1,+∞)C .(-∞,1]D .[1,+∞)3.命题:“∀x ∈R ,cos2x ≤cos 2x ”的否定为( )A .∀x ∈R ,cos2x >cos 2xB .∃x ∈R ,cos2x >cos 2xC .∀x ∈R ,cos2x <cos 2xD .∃x ∈R ,cos2x ≤cos 2x4.设a ,b ∈R ,则f (x )=x |sin x +a |-b 是奇函数的充要条件是( )A .a 2+b 2=0B .ab =0C.b a =0D .a 2-b 2=05.给出下列三个命题:①∀x ∈R ,x 2>0;②∃x 0∈R ,使得x 20≤x 0成立;③对于集合M ,N ,若x ∈M ∩N ,则x ∈M 且x ∈N .其中真命题的个数是( )A .0B .1C .2D .36.已知命题p :抛物线y =2x 2的准线方程为y =-12;命题q :若函数f (x +1)为偶函数,则f (x )关于直线x =1对称.则下列命题是真命题的是( )A .p ∧qB .p ∨(綈q )C .(綈p )∧(綈q )D .p ∨q7.已知集合A =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪46-x ∈N ,x ∈N ,则集合A 的子集的个数是________. 8.下列结论:①2∈{x |x =a +b 2,a ,b ∈Z };②3∈{x |x =2+a 3,a ∈R };③i ∈{x |x =a +b i ,a ,b ∈C };④1+i ∉{x |x =a +b i ,a ,b ∈C }.其中正确的序号是________.专题限时集训(一)B[第1讲 集合与常用逻辑用语](时间:10分钟+25分钟)2012二轮精品提分必练1.已知集合A ={x |x ≤3},B ={x |x ≥a }且A ∪B =R ,则实数a 的取值范围是( )A .(3,+∞)B .(-∞,3]C .[3,+∞)D .R2.设集合A ={x |x 2+2x -8<0},B ={x |x <1},则图1-1中阴影部分表示的集合为( )2012二轮精品提分必练图1-1A .{x |x ≥1}B .{x |-4<x <2}C .{x |-8<x <1}D .{x |1≤x <2}3.设向量a =(1,x -1),b =(x +1,3),则“x =2”是“a ∥b ”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.已知命题“函数f (x )和g (x )的定义域是R ,h (x )=f (x )·g (x ),如果f (x )、g (x )均为奇函数,那么h (x )为偶函数”的原命题、逆命题、否命题、逆否命题中,正确命题的个数是( )A .0B .1C .2D .32012二轮精品提分必练1.已知集合A ={0,1},B ={-1,0,a +3},且A ⊆B ,则a 等于( )A .1B .0C .-2D .-32.已知集合A ={x |x ≥3},B ={x |(x -2)(x -4)<0},则A ∩B =( )A .{x |x <2}B .{x |3≤x <4}C .{x |3≤x ≤4}D .{x |x >4}3.已知集合M ={x |y =3x -1},N ={x |y =log 2(x -2x 2)},则∁R (M ∩N )=( )A.⎝⎛⎭⎫13,12B.⎝⎛⎭⎫-∞,13∪⎣⎡⎭⎫12,+∞ C.⎣⎡⎦⎤0,12 D .(-∞,0]∪⎣⎡⎭⎫12,+∞ 4.“a <0且-1<b <0”是“a +ab <0”的( )A .充要条件B .必要不充分条件C .充分不必要条件D .既不充分也不必要条件5.设p :f (x )=x 3+2x 2+mx +1在R 上单调递增;q :m ≥8x x 2+4对任意x >0恒成立,则p 是q 的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件6.不等式1x-1<1的解集记为p,关于x的不等式x2+(a-1)x-a>0的解集记为q,已知p是q的充分不必要条件,则实数a的取值范围是()A.(-2,-1] B.[-2,-1]C.∅D.[-2,+∞)7.已知集合A={(x,y)|x2+y2=1},B={(x,y)|kx-y-2≤0},其中x,y∈R.若A⊆B,则实数k的取值范围是________.8.设X n={1,2,3,…,n}(n∈N*),对X n的任意非空子集A,定义f(A)为A中的最大元素,当A取遍X n的所有非空子集时,对应的f(A)的和为S n,则S2=________;S n=________.2012二轮精品提分必练专题限时集训(一)A【基础演练】1.D【解析】由题意知A∩B={a},故0<a<1.2.A【解析】结合维恩图(如图)可得当N∩∁I M=∅时,N⊆M,所以M∪N=M.2012二轮精品提分必练3.A【解析】当x≥2且y≥2时,一定有x2+y2≥4;反过来当x2+y2≥4,不一定有x≥2且y≥2,例如x=-4,y=0也可以,故选A.4.A 【解析】 特称命题的否定是全称命题,且结论的否定是2n ≤1000.【提升训练】1.C 【解析】 由集合的互异性得a 2≠a ,所以a ≠0或a ≠1,又M ∩N =N ,所以a =-1.2.B 【解析】 集合A =(0,1],集合B =(-∞,0],A ∪B =(-∞,1],所以∁U (A ∪B )=(1,+∞).3.B 【解析】 已知的命题是全称命题,其否定是特称命题.4.A 【解析】 由f (0)=0得b =0,由f ⎝⎛⎭⎫-π2=-f ⎝⎛⎭⎫π2得-π2|-1+a |=-π2|1+a |,即|a -1|=|a +1|,解得a =0.故a 2+b 2=0.5.C 【解析】 当x =0,x 2=0,命题①不正确;x 2≤x 的解是0≤x ≤1,只要x 0∈[0,1]即可,命题②正确;根据交集的定义,命题③正确.6.D 【解析】 命题p 是假命题;而命题q :由于函数f (x +1)是偶函数,这个函数图象关于y 轴对称,把这个函数图象向右平移一个单位即得函数f (x )的图象,故函数f (x )的图象关于直线x =1对称.所以命题q 是真命题,所以有p ∨q 为真.7.8 【解析】 由题意可知6-x 是4的正约数,所以6-x 可以是1,2,4;相应的x 为2,4,5,所以A ={2,4,5},所以集合A 的子集的个数是8.8.①②③ 【解析】 令a =0,b =1,则a +b 2=2,故2∈{x |x =a +b 2,a ,b∈Z };令a =3-23,则2+a 3=3,故3∈{x |x =2+a 3,a ∈R };令a =0,b =1,则a +b i =i ,故i ∈{x |x =a +b i ,a ,b ∈C };令a =1,b =1,则a +b i =1+i ,故1+i ∈{x |x =a +b i ,a ,b ∈C }.专题限时集训(一)B【基础演练】1.B 【解析】 结合数轴只需a ≤3即可.2.D 【解析】 由题图得阴影部分是A ∩(∁R B ).∵集合A ={x |-4<x <2},∁R B ={x |x ≥1},所以A ∩∁R B ={x |1≤x <2}.3.A 【解析】 当向量a ,b 平行时,x 满足1×3=(x -1)(x +1),解得x =±2.故“x =2”是“a ∥b ”的充分不必要条件.4.C 【解析】 由f (x )、g (x )均为奇函数可得h (x )=f (x )·g (x )为偶函数,反之则不成立,如h (x )=x 2-1是偶函数,但函数f (x )=x +1,g (x )=x -1都不是奇函数,故逆命题不正确,故其否命题也不正确,即只有原命题和逆否命题正确.正确选项C.【提升训练】1.C 【解析】 因为A ⊆B ,所以a +3=1,所以a =-2.2.B 【解析】 因为集合B ={x |2<x <4},所以A ∩B ={x |3≤x <4}. 3.B 【解析】 集合M ,N 都是函数的定义域,其中M =⎣⎡⎭⎫13,+∞,N =⎝⎛⎭⎫0,12,所以M ∩N =⎣⎡⎭⎫13,12,其在实数集合中补集∁R (M ∩N )=⎝⎛⎭⎫-∞,13∪⎣⎡⎭⎫12,+∞. 4.C 【解析】 不等式-1<b <0,即0<b +1<1,根据不等式的性质,a (b +1)<0,即a +ab <0,条件是充分的;a +ab <0,即a (b +1)<0,则即可a >0,b +1<0,也可a <0,b +1>0,故条件不是必要的.5.B 【解析】 f (x )在R 上单调递增,则f ′(x )≥0在R 上恒成立,即3x 2+4x +m ≥0对任意x 恒成立,故Δ≤0,即m ≥43;m ≥8x x 2+4对任意x >0恒成立,即m ≥⎝⎛⎭⎫8x x 2+4max ,8x x 2+4=8x +4x ≤824=2,即m ≥2.当命题p 成立时命题q 不一定成立,即p 不是q 的充分条件,但如果命题p 不成立,即m <43时,命题q 一定不成立,即条件是必要的. 6.A 【解析】 不等式1x -1<1等价于1x -1-1<0,即x -2x -1>0,解得x >2或x <1;不等式x 2+(a -1)x -a >0可以化为(x -1)(x +a )>0,当-a ≤1时,不等式的解集是x >1或x <-a ,此时a =-1,当-a >1时,不等式(x -1)(x +a )>0的解集是x <1或x >-a ,此时-a <2,即-2<a <-1.综合知-2<a ≤-1.7.[-3,3] 【解析】 根据集合的意义,集合A 可以看作坐标平面内的单位圆上的点,集合B 可以看作是坐标平面内的半平面上的点集,数形结合解决.方法1:本题的实质是圆x 2+y 2=1在直线kx -y -2=0的上方,直线kx -y -2=0是斜率为k ,在y 轴上的截距为-2的直线,根据图形可知k ∈[-3,3].方法2:根据子集的定义,本题中A ⊆B 即集合A 中的任意一元素都在集合B 中,我们不妨设集合A 中的x =cos θ,y =sin θ,说明k cos θ-sin θ-2≤0对任意θ恒成立,即k 2+1sin(θ+φ)≤2对任意θ恒成立,即k 2+1≤2恒成立,即-3≤k ≤ 3.8.5 (n -1)2n +1 【解析】 因为集合{1,2}的非空子集为{1},{2},{1,2},所以S 2=2×2+1=5.因为最大元素为n 的非空子集有2n -1个,最大元素为n -1的非空子集有2n -2个,…,最大元素为2的非空子集有2个,最大元素为1的非空子集有1个.所以S n =n ·2n -1+(n -1)·2n -2+…+2×2+1=(n -1)2n +1.。
智才艺州攀枝花市创界学校100天冲刺第82天一、选择题。
1.不等式组5315+15 3.x y y x x y +≤⎧⎪≤⎨⎪-≤⎩,,表示的平面区域的面积为〔〕 A .7B .5C .3D .142.数列52,,11,22,5,2则 是这个数列的〔〕A .第6项B .第7项C .第19项D .第11项3.:p R x ∃∈,2lg x x ->:q R x ∀∈,1x e >,那么〔〕 A p q ∨B p q ∧C ()p q ∧⌝D ()p q ∨⌝4.设变量x ,y 满足约束条件:,4,2,y x x x ⎧⎪⎨⎪⎩≥+3y ≤≥-那么z =|x -3y |的最大值为〔〕.A .10B .8C .6D .45.向量,,a b c 满足4,22,a b ==a 与b 的夹角为4π,()()1c a c b -⋅-=-,那么c a-的最大值为〔〕 〔A 12〔B 1〔C〔D 1+ 6.复数1z i =-,那么1z z+对应的点所在的象限为〔〕 A .第一象限B .第二象限C .第三象限D .第四象限7.在ABC ∆中,内角A ,B ,C 的对边分别为a ,b ,c ,且sin b A =3cos a B .那么B =〔〕 A .6πB .4πC .3πD .2π 8.两直线0x ky k--=与(1)y k x =-平行,那么k 的值是〔〕 A .1B .-1C .1或者-1D .2二、填空题。
9.在△ABC 中,A=60°,AC=4,BC=2,那么△ABC 的面积等于_____. 10.等比数列{a n }中,a 1+a 2=9,a 1a 2a 3=27,那么{a n }的前n 项和nS =。
三、解答题。
11.〔本小题总分值是12分〕如下列图,在四边形ABCD 中,B D ∠=∠2,且1=AD ,3=CD ,33cos =B .〔1〕求ACD ∆的面积;〔2〕假设32=BC ,求AB 的长.12.设数列{a n }满足a 1=3,a n +1=a n 2-2na n +2,n =1,2,3,…(1)求a 2,a 3,a 4的值,并猜想数列{a n }的通项公式(不需证明);(2)记S n 为数列{a n }的前n 项和,试求使得S n <2n成立的最小正整数n ,并给出证明. 参考答案4.B【解析】不等式组所表示的平面区域为如下列图的三角形ABC ,作直线03=-y x ,将直线在三角形ABC 区域平移,可知在直线43=+y x 与直线2-=x 的交点)2,2(-A 可获得z =|x -3y |的最大值为62--=8.【解析】当0=k时,两直线垂直,那么0≠k ,直线0x ky k --=化为斜截式11-=x k y ,斜率为k 1-,截距为1-,而直线(1)y k x =-斜率为k ,截距为k -,二直线平行,那么⎪⎩⎪⎨⎧-≠--=-11k k k 1-=⇒k 9.【解析】在△ABC 中,由余弦定理知2222cos BCAB AC AB AC A =+-⋅ 即12=2AB +16-2×4×AB ×cos60°,2AB -4AB+4=0,解得AB=2.所以11sin 2422ABCS AB AC A ∆=⋅=⨯⨯= 10.112(1)2n - 【解析】∵a 1a 2a 3=27,∴a 2=3,又∵a 1+a 2=9∴a 1=6,公比q=12 ∴611121121122n n n S ⎡⎤⎛⎫ ⎪⎢⎥-==--⎡⎤⎝⎭⎣⎦⎢⎥⎣⎦()故答案为112(1)2n -. 〔2〕S n =n 2+2n 见解析 【解析】解:(1)a 2=5,a 3=7,a 4=9,猜想a n =2n +1.(2)S n =()3212n n ++=n 2+2n , 使得S n <2n 成立的最小正整数n =6.证明:n ≥6(n ∈N *)时都有2n >n 2+2n. ①n =6时,26>62+2×6,即64>48成立;②假设n=k(k≥6,k∈N*)时,2k>k2+2k成立,那么2k+1=2·2k>2(k2+2k)=k2+2k+k2+2k>k2+2k+3+2k=(k+1)2+2(k+1),即n=k+1时,不等式成立;由①、②可得,对于所有的n≥6(n∈N*)都有2n>n2+2n成立.。
§11.2 古典概型1.基本事件的特点(1)任何两个基本事件是互斥的.(2)任何事件(除不可能事件)都可以表示成基本事件的和. 2.古典概型具有以下两个特点的概率模型称为古典概率模型,简称古典概型. (1)试验中所有可能出现的基本事件只有有限个. (2)每个基本事件出现的可能性相等.3.如果一次试验中可能出现的结果有n 个,而且所有结果出现的可能性都相等,那么每一个基本事件的概率都是 1n;如果某个事件A 包括的结果有m 个,那么事件A 的概率P (A )= m n .4.古典概型的概率公式P (A )=A 包含的基本事件的个数基本事件的总数.1.判断下面结论是否正确(请在括号中打“√”或“×”)(1)“在适宜条件下,种下一粒种子观察它是否发芽”属于古典概型,其基本事件是“发芽与不发芽”.( × )(2)掷一枚硬币两次,出现“两个正面”“一正一反”“两个反面”,这三个结果是等可能事件.( × )(3)从市场上出售的标准为500±5 g 的袋装食盐中任取一袋,测其重量,属于古典概型.( × )2.(2013·某某)集合A ={2,3},B ={1,2,3},从A 、B 中各任意取一个数,则这两数之和等于4的概率是( ) A.23B.12C.13D.16 答案 C解析 从A 、B 中任意取一个数,共有6种情形,两数和等于4的情形只有(2,2),(3,1)两种,∴P =26=13.3.一个口袋内装有2个白球和3个黑球,则先摸出1个白球后放回的条件下,再摸出1个白球的概率是( ) A.23B.14C.25D.15 答案 C解析 先摸出1个白球后放回,再摸出1个白球的概率,实质上就是第二次摸到白球的概率,因为袋内装有2个白球和3个黑球,因此概率为25.4.(2013·某某)若甲、乙、丙三人随机地站成一排,则甲、乙两人相邻而站的概率为________.答案 23解析 甲、乙、丙三人随机地站成一排,共有甲、乙、丙,甲、丙、乙,乙、甲、丙,乙、丙、甲,丙、甲、乙,丙、乙、甲共6种排法,其中甲、乙两人相邻而站共甲、乙、丙,乙、甲、丙,丙、甲、乙,丙、乙、甲4种排法,故P =46=23.5.从1,2,3,4,5,6这6个数字中,任取2个数字相加,其和为偶数的概率是________.答案 25解析 从6个数中任取2个数的可能情况有(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),共15种,其中和为偶数的情况有(1,3),(1,5),(2,4),(2,6),(3,5),(4,6),共6种,所以所求的概率是25.题型一 基本事件与古典概型的判断例1 袋中有大小相同的5个白球,3个黑球和3个红球,每球有一个区别于其他球的编号,从中摸出一个球.(1)有多少种不同的摸法?如果把每个球的编号看作一个基本事件建立概率模型,该模型是不是古典概型?(2)若按球的颜色为划分基本事件的依据,有多少个基本事件?以这些基本事件建立概率模型,该模型是不是古典概型?思维启迪 判断一个概率模型是否为古典概型的依据是古典概型的“有限性”和“等可能性”.解 (1)由于共有11个球,且每个球有不同的编号,故共有11种不同的摸法. 又因为所有球大小相同,因此每个球被摸中的可能性相等, 故以球的编号为基本事件的概率模型为古典概型.(2)由于11个球共有3种颜色,因此共有3个基本事件,分别记为A:“摸到白球”,B:“摸到黑球”,C:“摸到红球”,,而白球有5个,又因为所有球大小相同,所以一次摸球每个球被摸中的可能性均为111故一次摸球摸到白球的可能性为5,11,同理可知摸到黑球、红球的可能性均为311显然这三个基本事件出现的可能性不相等,所以以颜色为划分基本事件的依据的概率模型不是古典概型.思维升华古典概型需满足两个条件:①对于每次随机试验来说,只可能出现有限个不同的试验结果;②对于所有不同的试验结果而言,它们出现的可能性是相等的.(1)下列问题中是古典概型的是()A.种下一粒杨树种子,求其能长成大树的概率B.掷一颗质地不均匀的骰子,求出现1点的概率C.在区间[1,4]上任取一数,求这个数大于1.5的概率D.同时掷两颗骰子,求向上的点数之和是5的概率(2)将一枚硬币抛掷三次共有________种结果.答案(1)D(2)8解析(1)A、B两项中的基本事件的发生不是等可能的;C项中基本事件的个数是无限多个;D项中基本事件的发生是等可能的,且是有限个.(2)设出现正面为1,反面为0,则共有(1,1,1),(1,1,0),(1,0,1),(1,0,0),(0,1,1),(0,1,0),(0,0,1),(0,0,0)8种结果.题型二古典概型的概率例2(2013·某某)某小组共有A,B,C,D,E五位同学,他们的身高(单位:米)及体重指标(2)如下表所示:A B C D E身高 1.69 1.73 1.75 1.79 1.82体重指标19.225.118.523.320.9(1)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率;(2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.思维启迪计算基本事件总数或计算某一事件包含的基本事件数时,可以用列举的方法,列举时要不重不漏.解(1)从身高低于1.80的4名同学中任选2人,其一切可能的结果组成的基本事件有(A,B),(A,C),(A,D),(B,C),(B,D),(C,D)共6个.设“选到的2人身高都在1.78以下”为事件M ,其包括事件有3个,故P (M )=36=12.(2)从小组5名同学中任选2人,其一切可能的结果组成的基本事件有(A ,B ),(A ,C ),(A ,D ),(A ,E ),(B ,C ),(B ,D ),(B ,E ),(C ,D ),(C ,E ),(D ,E )共10个.设“选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)”为事件N ,且事件N 包括事件有(C ,D ),(C ,E ),(D ,E )共3个.则P (N )=310.思维升华 求古典概型的概率的关键是求试验的基本事件的总数和事件A 包含的基本事件的个数,这就需要正确列出基本事件,基本事件的表示方法有列举法、列表法和树形图法,具体应用时可根据需要灵活选择.某次会议有6名代表参加,A 、B 两名代表来自甲单位,C 、D 两名代表来自乙单位,E 、F 两名代表来自丙单位,现随机选出两名代表发言,求: (1)代表A 被选中的概率是多少?(2)选出的两名代表中,恰有1名来自乙单位或2名都来自丙单位的概率是多少? 解 (1)从这6名代表中随机选出2名,共有15种不同的选法,分别为(A ,B ),(A ,C ),(A ,D ),(A ,E ),(A ,F ),(B ,C ),(B ,D ),(B ,E ),(B ,F ),(C ,D ),(C ,E ),(C ,F ),(D ,E ),(D ,F ),(E ,F ).其中代表A 被选中的选法有(A ,B ),(A ,C ),(A ,D ),(A ,E ),(A ,F ),共5种.故代表A 被选中的概率为515=13.(2)随机选出的两名代表中,恰有1名来自乙单位或2名都来自丙单位的结果有9种,分别是(A ,C ),(A ,D ),(B ,C ),(B ,D ),(C ,E ),(C ,F ),(D ,E ),(D ,F ),(E ,F ).所以“恰有1名来自乙单位或2名都来自丙单位”这一事件的概率为915=35.题型三 古典概型与统计的综合应用例3(2013·某某)有7位歌手(1至7号)参加一场歌唱比赛,由500名大众评委现场投票决定组别 A B C D E 人数5010015015050(1)为了调查评委对7位歌手的支持情况,现用分层抽样方法从各组中抽取若干评委,其中从B 组别 A B C D E 人数 50 100 150 150 50 抽取人数6(2)在(1)中,若A ,B 两组被抽到的评委中各有2人支持1号歌手,现从这两组被抽到的评委中分别任选1人,求这2人都支持1号歌手的概率.思维启迪 各组抽取人数的比率是相等的,因此,由B 组抽取的比率可求得其它各组抽取的人数.解 (1)由题设知,分层抽样的抽取比例为6%,所以各组抽取的人数如下表:组别 A B C D E 人数 50 100 150 150 50 抽取人数36993(2)记从A 组抽到的3个评委为a 1,a 2,a 3,其中a 1,a 2支持1号歌手;从B 组抽到的6个评委为b 1,b 2,b 3,b 4,b 5,b 6,其中b 1,b 2支持1号歌手.从{a 1,a 2,a 3}和{b 1,b 2,b 3,b 4,b 5,b 6}中各抽取1人的所有结果为由以上树状图知所有结果共18种,其中2人都支持1号歌手的有a 1b 1,a 1b 2,a 2b 1,a 2b 2共4种,故所求概率P =418=29.思维升华 有关古典概型与统计结合的题型是高考考查概率的一个重要题型,已成为高考考查的热点,概率与统计结合题,无论是直接描述还是利用概率分布表、分布直方图、茎叶图等给出信息,只需要能够从题中提炼出需要的信息,则此类问题即可解决.为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:(1)估计该校男生的人数;(2)估计该校学生身高在170~185 cm 之间的概率;(3)从样本中身高在180~190 cm 之间的男生中任选2人,求至少有1人身高在185~190 cm 之间的概率.解 (1)样本中男生人数为40,由分层抽样比例为10%估计全校男生人数为400. (2)由统计图知,样本中身高在170~185 cm 之间的学生有14+13+4+3+1=35(人),样本容量为70,所以样本中学生身高在170~185 cm 之间的频率f =3570=0.5.故由f 估计该校学生身高在170~185 cm 之间的概率P =0.5.(3)样本中身高在180~185 cm 之间的男生有4人,设其编号为①②③④,样本中身高在185~190 cm 之间的男生有2人,设其编号为⑤⑥.从上述6人中任选2人的树状图为故从样本中身高在180~190 cm 之间的男生中任选2人的所有可能结果数为15,至少有1人身高在185~190 cm 之间的可能结果数为9,因此,所求概率P =915=0.6.六审细节更完善典例:(12分)一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4. (1)从袋中随机取两个球,求取出的球的编号之和不大于4的概率;(2)先从袋中随机取一个球,该球的编号为m ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n ,求n <m +2的概率.(1)基本事件为取两个球↓(两球一次取出,不分先后,可用集合的形式表示) 把取两个球的所有结果列举出来 ↓{1,2},{1,3},{1,4},{2,3},{2,4},{3,4} ↓两球编号之和不大于4(注意:和不大于4,应为小于4或等于4) ↓{1,2},{1,3}↓利用古典概型概率公式P =26=13(2)两球分两次取,且有放回↓(两球的编号记录是有次序的,用坐标的形式表示) 基本事件的总数可用列举法表示 ↓(1,1),(1,2),(1,3),(1,4) (2,1),(2,2),(2,3),(2,4) (3,1),(3,2),(3,3),(3,4) (4,1),(4,2),(4,3),(4,4)↓(注意细节,m 是第一个球的编号,n 是第2个球的编号) n <m +2的情况较多,计算复杂 (将复杂问题转化为简单问题)↓计算n ≥m +2的概率↓n ≥m +2的所有情况为(1,3),(1,4),(2,4)↓P 1=316(注意细节,P 1=\f(3,16)是n ≥m +2的概率,需转化为其对,立事件的概率)n <m +2的概率为1-P 1=1316.规X 解答解 (1)从袋中随机取两个球,其一切可能的结果组成的基本事件有{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},共6个.从袋中取出的球的编号之和不大于4的事件共有{1,2},{1,3}两个.因此所求事件的概率P =26=13.[4分] (2)先从袋中随机取一个球,记下编号为m ,放回后,再从袋中随机取一个球,记下编号为n ,其一切可能的结果(m ,n )有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个.[6分]又满足条件n ≥m +2的事件为(1,3),(1,4),(2,4),共3个,所以满足条件n ≥m +2的事件的概率为P 1=316.[10分]故满足条件n <m +2的事件的概率为1-P 1=1-316=1316.[12分]温馨提醒 (1)本题在审题时,要特别注意细节,使解题过程更加完善.如第(1)问,注意两球一起取,实质上是不分先后,再如两球编号之和不大于4等;第(2)问,有次序.(2)在列举基本事件空间时,可以利用列举、画树状图等方法,以防遗漏.同时要注意细节,如用列举法,第(1)问应写成{1,2}的形式,表示无序,第(2)问应写成(1,2)的形式,表示有序.(3)本题解答时,存在格式不规X ,思维不流畅的严重问题.如在解答时,缺少必要的文字说明,没有按要求列出基本事件.在第(2)问中,由于不能将事件n <m +2的概率转化成n ≥m +2的概率,导致数据复杂、易错.所以按要求规X 解答是做好此类题目的基本要求.方法与技巧1.古典概型计算三步曲第一,本试验是否是等可能的;第二,本试验的基本事件有多少个;第三,事件A 是什么,它包含的基本事件有多少个. 2.确定基本事件的方法列举法、列表法、树状图法. 失误与防X1.古典概型的重要思想是事件发生的等可能性,一定要注意在计算基本事件总数和事件包括的基本事件个数时,它们是否是等可能的. 2.概率的一般加法公式:P (A ∪B )=P (A )+P (B )-P (A ∩B ).公式使用中要注意:(1)公式的作用是求A ∪B 的概率,当A ∩B =∅时,A 、B 互斥,此时P (A ∩B )=0,所以P (A ∪B )=P (A )+P (B );(2)要计算P (A ∪B ),需要求P (A )、P (B ),更重要的是把握事件A ∩B ,并求其概率;(3)该公式可以看作一个方程,知三可求一.A 组 专项基础训练一、选择题1.(2013·课标全国Ⅰ)从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是( )A.12B.13C.14D.16 答案 B解析 基本事件的总数为6,构成“取出的2个数之差的绝对值为2”这个事件的基本事件的个数为2,所以所求概率P =26=13,故选B.2.甲乙两人一起去游泰山,他们约定,各自独立地从1到6号景点中任选4个进行游览,每个景点参观1小时,则最后一小时他们同在一个景点的概率是( ) A.136B.19C.536D.16 答案 D解析 最后一个景点甲有6种选法,乙有6种选法,共有36种,他们选择相同的景点有6种,所以P =636=16,所以选D.3.(2013·某某)若某公司从五位大学毕业生甲、乙、丙、丁、戊中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率为( )A.23B.25C.35D.910 答案 D解析 由题意知,从五位大学毕业生中录用三人,所有不同的可能结果有(甲,乙,丙),(甲,乙,丁),(甲,乙,戊),(甲,丙,丁),(甲,丙,戊),(甲,丁,戊),(乙,丙,丁),(乙,丙,戊),(乙,丁,戊),(丙,丁,戊),共10种,其中“甲与乙均未被录用”的所有不同的可能结果只有(丙,丁,戊)这1种,故其对立事件“甲或乙被录用”的可能结果有9种,所求概率P =910.4.第12届全运会于2013年在某某举行,运动会期间来自A 大学2名和B 大学4名共计6名大学生志愿者,现从这6名志愿者中随机抽取2人到体操比赛场馆服务,至少有一名A 大学志愿者的概率是( ) A.115B.25C.35D.1415 答案 C解析 记2名来自A 大学的志愿者为A 1,A 2,4名来自B 大学的志愿者为B 1,B 2,B 3,B 4.从这6名志愿者中选出2名的基本事件有(A 1,A 2),(A 1,B 1),(A 1,B 2),(A 1,B 3),(A 1,B 4),(A 2,B 1),(A 2,B 2),(A 2,B 3),(A 2,B 4),(B 1,B 2),(B 1,B 3),(B 1,B 4),(B 2,B 3),(B 2,B 4),(B 3,B 4),共15种.其中至少有一名A 大学志愿者的事件有9种.故所求概率P =915=35.故选C.5.连掷两次骰子分别得到点数m 、n ,则向量(m ,n )与向量(-1,1)的夹角θ>90°的概率是( )A.512B.712C.13D.12 答案 A解析 ∵(m ,n )·(-1,1)=-m +n <0,∴m >n .基本事件总共有6×6=36(个),符合要求的有(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),…,(5,4),(6,1),…,(6,5),共1+2+3+4+5=15(个).∴P =1536=512,故选A.二、填空题6.将一颗骰子投掷两次分别得到点数a ,b ,则直线ax -by =0与圆(x -2)2+y 2=2相交的概率为________.答案 512解析 圆心(2,0)到直线ax -by =0的距离d =|2a |a 2+b 2,当d <2时,直线与圆相交,则有d =|2a |a 2+b 2<2,得b >a ,满足b >a 的,共有15种情况,因此直线ax -by =0与圆(x -2)2+y 2=2相交的概率为1536=512.7.从长度分别为2、3、4、5的四条线段中任意取出三条,则以这三条线段为边可以构成三角形的概率是________.答案 34解析从四条线段中任取三条有4种取法:(2,3,4),(2,3,5),(2,4,5),(3,4,5),其中能构成三角形的取法有3种:(2,3,4),(2,4,5),(3,4,5),故所求的概率为34.8.用两种不同的颜色给图中三个矩形随机涂色,每个矩形只涂一种颜色,则相邻两个矩形涂不同颜色的概率是________.答案1 4解析由于只有两种颜色,不妨将其设为1和2,若只用一种颜色有111;222.若用两种颜色有122;212;221;211;121;112.所以基本事件共有8种.又相邻颜色各不相同的有2种,故所求概率为14.三、解答题9.设连续掷两次骰子得到的点数分别为m,n,令平面向量a=(m,n),b=(1,-3).(1)求使得事件“a⊥b”发生的概率;(2)求使得事件“|a|≤|b|”发生的概率.解(1)由题意知,m∈{1,2,3,4,5,6},n∈{1,2,3,4,5,6},故(m,n)所有可能的取法共36种.a⊥b,即m-3n=0,即m=3n,共有2种:(3,1)、(6,2),所以事件a⊥b的概率为236=1 18.(2)|a|≤|b|,即m2+n2≤10,共有(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(3,1)6种,其概率为636=1 6.10.(2013·某某)某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,(1)利用上表提供的样本数据估计该批产品的一等品率;(2)在该样本的一等品中,随机抽取2件产品.①用产品编号列出所有可能的结果;②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率.解(1)计算10件产品的综合指标S,如下表:S 4 4 6 3 4 5 4 5 3 5其中S ≤4的有A 1,A 2,A 4,A 5,A 7,A 9,共6件,故该样本的一等品率为610=0.6,从而可估计该批产品的一等品率为0.6.(2)①在该样本的一等品中,随机抽取2件产品的所有可能结果为{A 1,A 2},{A 1,A 4},{A 1,A 5},{A 1,A 7},{A 1,A 9},{A 2,A 4},{A 2,A 5},{A 2,A 7},{A 2,A 9},{A 4,A 5},{A 4,A 7},{A 4,A 9},{A 5,A 7},{A 5,A 9},{A 7,A 9},共15种.②在该样本的一等品中,综合指标S 等于4的产品编号分别为A 1,A 2,A 5,A 7,则事件B 发生的所有可能结果为{A 1,A 2},{A 1,A 5},{A 1,A 7},{A 2,A 5},{A 2,A 7},{A 5,A 7},共6种. 所以P (B )=615=25.B 组 专项能力提升1.从正六边形的6个顶点中随机选择4个顶点,则以它们作为顶点的四边形是矩形的概率等于( )A.110B.18C.16D.15 答案 D解析 如图所示,从正六边形ABCDEF 的6个顶点中随机选4个顶点,可以看作随机选2个顶点,剩下的4个顶点构成四边形,有A 、B ,A 、C ,A 、D ,A 、E ,A 、F ,B 、C ,B 、D ,B 、E ,B 、F ,C 、D ,C 、E ,C 、F ,D 、E ,D 、F ,E 、F ,共15种.若要构成矩形,只要选相对顶点即可,有A 、D ,B 、E ,C 、F ,共3种,故其概率为315=15.2.将一骰子向上抛掷两次,所得点数分别为m 和n ,则函数y =23mx 3-nx +1在[1,+∞)上为增函数的概率是( ) A.12B.23C.34D.56 答案 D解析 所有事件有6×6=36(种),若满足条件, 则y ′=2mx 2-n ≥0对x ≥1恒成立, 又m >0,即(2mx 2-n )min =2m -n ,即2m ≥n ,而2m <n 有(1,3),(1,4),(1,5),(1,6),(2,5),(2,6),共6种,则2m ≥n 共30种.∴P =3036=56.3.一个袋子中有5个大小相同的球,其中3个白球2个黑球,现从袋中任意取出一个球,取出后不放回,然后再从袋中任意取出一个球,则第一次为白球、第二次为黑球的概率为( )A.35B.310C.12D.625 答案 B解析 设3个白球分别为a 1,a 2,a 3,2个黑球分别为b 1,b 2,则先后从中取出2个球的所有可能结果为(a 1,a 2),(a 1,a 3),(a 1,b 1),(a 1,b 2),(a 2,a 3),(a 2,b 1),(a 2,b 2),(a 3,b 1),(a 3,b 2),(b 1,b 2),(a 2,a 1),(a 3,a 1),(b 1,a 1),(b 2,a 1),(a 3,a 2),(b 1,a 2),(b 2,a 2),(b 1,a 3),(b 2,a 3),(b 2,b 1),共20种.其中满足第一次为白球、第二次为黑球的有(a 1,b 1),(a 1,b 2),(a 2,b 1),(a 2,b 2),(a 3,b 1),(a 3,b 2),共6种,故所求概率为620=310.4.袋中装有大小相同的总数为5的黑球、白球,若从袋中任意摸出2个球,至少得到1个白球的概率是910,则从中任意摸出2个球,得到的都是白球的概率为________.答案 310解析 因为袋中装有大小相同的总数为5的黑球、白球,若从袋中任意摸出2个球,共有10种情况,没有得到白球的概率为110,设白球个数为x ,则黑球个数为5-x ,那么可知白球有3个,黑球有2个,因此从中任意摸出2个球,得到的都是白球的概率为310.5.若集合A ={a |a ≤100,a =3k ,k ∈N *},集合B ={b |b ≤100,b =2k ,k ∈N *},在A ∪B 中随机地选取一个元素,则所选取的元素恰好在A ∩B 中的概率为________.答案 1667解析 易知A ={3,6,9,…,99},B ={2,4,6,…,100}, 则A ∩B ={6,12,18,…,96},其中有元素16个. A ∪B 中元素共有33+50-16=67(个),∴所求概率为1667.6.一汽车厂生产A ,B ,C 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆)按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A 类轿车10辆. (1)求z 的值;(2)用分层抽样的方法在C 类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;(3)用随机抽样的方法从B 类舒适型轿车中抽取8辆,经检测它们的得分如下: 9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率. 解 (1)设该厂这个月共生产轿车n 辆,由题意得50n =10100+300,所以n =2 000,则z =2 000-100-300-150-450-600=400. (2)设所抽样本中有a 辆舒适型轿车,由题意得4001 000=a5,则a =2.因此抽取的容量为5的样本中,有2辆舒适型轿车,3辆标准型轿车.用A 1,A 2表示2辆舒适型轿车,用B 1,B 2,B 3表示3辆标准型轿车,用E 表示事件“在该样本中任取2辆,其中至少有1辆舒适型轿车”,则基本事件空间包含的基本事件有(A 1,A 2),(A 1,B 1),(A 1,B 2),(A 1,B 3),(A 2,B 1),(A 2,B 2),(A 2,B 3),(B 1,B 2),(B 1,B 3),(B 2,B 3),共10个. 事件E 包含的基本事件有(A 1,A 2),(A 1,B 1),(A 1,B 2),(A 1,B 3),(A 2,B 1),(A 2,B 2),(A 2,B 3),共7个.故P (E )=710,即所求概率为710.(3)样本平均数x =18(9.4+8.6+9.2+9.6+8.7+9.3+9.0+8.2)=9.设D 表示事件“从样本中任取一个数,该数与样本平均数之差的绝对值不超过0.5”,则基本事件空间中有8个基本事件,事件D 包含的基本事件有9.4,8.6,9.2,8.7,9.3,9.0,共6个,所以P (D )=68=34,即所求概率为34.。
7 98 6 3 8 9 3 9 8 8 4 1 5 10 3 1 11 4 (第4题图1)(第4题图2)≤≥12015高考数学必做100题(含答案详解)一、选择题1.【2013成都二诊】命题“R x ∈∀.,都有ln(x2+1)>0”的否定为 ( ) (A) R x ∈∀,都有ln(x2 +1)≤0(B)Rx ∈∃0,使得ln(x02+1)>0(C) R x ∈∀,都有ln(x2+l)<0 (D) Rx ∈∃0,使得ln(x02+1)≤0【答案】D2.【2013四川雅安中学二诊】已知i 是虚数单位,则201311i i +⎛⎫⎪-⎝⎭的值是( )A .iB .i -C .1D .1- 【答案】 A3.【2013枣庄一模】下列命题的否定为假命题的是 A .2,220x R x x ∃∈++≤ B .任意一个四边形的四个顶点共圆C .所有能被3整除的整数都是奇数D .22,sin cos 1x R x x ∀∈+= 【答案】D4.【2013湖北八校二次联考】图1是某高三学生进入高中三年来的数学考试成绩的茎叶图,图中第1次到14次的考试成绩依次记为1214,,,.A A A 图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图。
那么算法流程图输出的结果是( ) A .7 B .8 C .9 D .105.【2013北京石景山3月统一测试】若复数(a -i )2在复平面内对应的点在y 轴负半轴上,则实数a 的值是( )A . 1B .-1CD .【答案】A6.【2013太原一模】已知函数2()1f x og x= ,若在[1,4]上随机取一个实数x0,则使得0()1f x ≥成立的概率为A .13B .12C .23D .34答案.C7. 【2013四川雅安中学二诊】设不等式组22,42x y x y -+≥≥-⎧⎪⎨⎪⎩0≤, 表示的平面区域为D .在区域D 内随机取一个点,则此点到直线+2=0y 的距离大于2的概率是( )A. 413【答案】D8.【2013R 上的可导函数,且R x ∈∀,均有)()(x f x f '>,则有( )A .B .C .D .【答案】D9.【2013枣庄一模】两旅客坐火车外出旅游,希望座位连在一起,且仅有一个靠窗,已知火车上的座位的排法如表格所示,则下列座位号码符合要求的是A .48,49B .62,63C .84,85D .75,76>2013(0),(2013)(0)e f f e f <<20132013(2013)f ->10.【2013湖北八校二次联考】《九章算术》之后,人们进一步用等差数列求和公式来解决更多的问题,《张丘建算经》卷上第22题为:“今有女善织,日益功疾(注:从第2天起每天比前一天多织相同量的布),第一天织5尺布,现在一月(按30天计),共织390尺布”,则从第2天起每天比前一天多织( )尺布. A .12B .815C .1631D .1629【答案】D11. 【2013广西四市3月联考】定义在(-1,1)上的函数)(x f 满足:⎪⎪⎭⎫⎝⎛--=-xy y x f y f x f 1)()(,当)0,1(-∈x 时,有0)(>x f ,若⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=11151f f a ,)0(f b =,)(2-=e f c ,则a,b,c 的大小关系为A. a c b >>B. b a c >>C. c b a >>D. c a b >>【答案】A12.【2013开封二模】函数12,41()),5,35,2(2),4x x f x a f b c xf x x ⎧->⎪====⎨⎪+≤⎩记则 A .a>b>c B .b<a<c C .a<c<bD .a>c>b【答案】D13、【2013梅州3月质检】下列命题中假命题是A 、x ∀>0,有ln 2x+lnx +1>0B 、,αβ∃∈R ,使cos()cos cos αβαβ+=+C 、“a 2<b 2”是“a <b ”的必要不充分条件D 、m R ∃∈,使243()(1)m m f x m x -+=-是幂函数,且在(0,+∞)上递减【答案】C14. 【2013浙江省金丽衢十二校二次联考】 已知ABC ∆的三个顶点C B A ,,及所在平面内一点P 满足PA PB PC AB ++=,则点P 与ABC ∆的关系A .P 在ABC ∆内部B .P 在ABC ∆外部 C .P 在边AB 上D .P 在边AC 上 【答案】D15. 【2013蚌埠二检】△ABC 的外接圆的圆的加以为O,半径为1,若2AB AC AO +=,且||||AO A C =,则向量BA在向量BC 方向上的射影的数量为( )A.32B.2C. 3D.-2【答案】A16.【2013宝鸡二模】下列命题中,真命题是( ) A.2cos sin ,2,0>+⎢⎣⎡⎥⎦⎤∈x x x 使存在π B.)(x x x 212,,3≥+∞+∈使存在 C.1,2-=∈x R x x 使存在 D.x x x < ⎝⎛⎥⎦⎤∈sin ,2,0使对任意π【答案】D17. 【2013汕头一模】设α、β为两个不同的平面,m 、n 为两条不同的直线,βα⊂⊂n m ,,有两个命题: P :若α//β、则m//n; q:若n 丄α,则α丄β;那么() A. “p 或q 是假命题 B. “ P 且q ”是真命题 C. “非p 或q 是假命题 D. “非p 且q 是真命题 【答案】D18.【2013烟台3月诊断】已知函数f(x)=20082cos(20000)32(2000)x x x x π-⎧≤⎪⎨⎪>⎩,则f[f (2013)]= AB .C .1D . -1【答案】D19、【2013梅州3月质检】某程序框图如右图所示,若输出的S =57,则判断框内填A 、k >4?B 、k >5?C 、k >6?D 、k >7? 【答案】A20.【2013郑州二模】―个锥体的主视图和左视图如图所示,下面选项中,不可能是该锥体的俯视图的是【答案】C21.【2013ASC=∠BSC=45°则棱锥S —ABCA 【答案】C22.【2013西安一模】若向量(23),(47),BA CA ==,,则BC = A .(-2,-4) B .(3.4)C .(6,10)D .(-6.-10)【答案】A23.【2013东北三校3月联考】已知全集U R =,集合{}|2A x x =≥,{|05}B x x =≤<,则集合)U C A B ⋂=( ( )A .{|02}x x <<B .{|02}x x <≤C .{|02}x x ≤<D .{|02}x x ≤≤【答案】C 。
100天冲刺 第 98 天
一、选择题。
1.已知集合{}{}
|(3)0,|1|2,A x x x B x x =-<=-<则“A x ∈”是“B x ∈”的( ) A.充分不必要条件 B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件 2.设x x x f ln )(=,若2)(0'=x f ,则=0x ( ) A .2e B .e C .22ln D .2ln
3.若正实数a b 、满足4a b +=,则22log log a b +的最大值是 ( )
A 、0
B 、 1
C
D 、2
4.已知ABC ∆中,3BC =,4AC =,5AB =,点P 是三边上的任意一点,m PA PB =⋅,则m 的最小值是( ) A .-25 B .25
4
-
C .94-
D .0
5.若(2,1)P -为圆15cos 5sin x y θ
θ=+⎧⎨=⎩
(θ为参数且02θπ≤<)的弦的中点,则该弦所在的
直线方程为( )
A .30x y --=
B .25x y +=
C .10x y +-=
D .250x y --= 6.已知数列{a n }的前n 项和n s 满足:n m n m s s s +=+,且1a =1.那么10a =( )
A .1
B .9
C .10
D .55
7.在一个2×2列联表中,由其数据计算得到K 2
的观测值k =13.097,则其两个变量间有关系的可能性为( )
A .99.9%
B .95%
C .90%
D .0 附表:
8.已知⎩⎨
⎧∉+∈+=R
x x i R
x x x f ,)1(,1)(,则=-))1((i f f ( )
A.2i -
B.1
C.3
D.3i +
二、填空题。
9.已知两条平行直线1l :m y =和2l :3
1
y m =
+(这里0>m ),且直线1l 与函数2log y x =的图像从左至右相交于点A 、B ,直线2l 与函数8log y x =的图像从左至右相交于C 、D .若记线段AC 和BD 在x 轴上的投影长度分别为 a 、b ,则当m 变化时,b
a
的最小值为 .
10.若变量,x y 满足约束条件329
69x y x y ≤+≤⎧⎨≤-≤⎩,则2z x y =+的最小值为 .
三、解答题。
11.若实数x 、y 、m 满足|x -m|>|y -m|,则称x 比y 远离m.
(1)若x 2
-1比1远离0,求x 的取值范围;
(2)对任意两个不相等的正数a 、b ,证明:a 3
+b 3
比a 2
b +ab 2
远离
12.(本小题满分14分)已知函数32
41)(1+-=-x x x f λ
(21≤≤-x ). (1)若3
2
λ=
时,求函数)(x f 的值域; (2)若函数)(x f 的最小值是1,求实数λ的值.
参考答案
1.A
【解析】由题意知,集合}30{<<=x x A ,}31{<<-=x x B ,所以B A ⊆,且B A ≠,所以“A x ∈”能推出“B x ∈”,但“B x ∈”不能推出“A x ∈”,所以“A x ∈”是“B x ∈”
的充分不必要条件.故应选A . 2. B
【解析】因为所求的2
13.09710.828k =>,故可能性为99.9%,所以选A.
8.C
【解析】因为2)1)(1()1(=-+=-i i i f ,所以321)2())1((=+==-f i f f ,故应选C . 9.32
【解析】由题意得:3311
|28|,|28|m m m m b a --++=-=-,则3
39
1
11
3128||28228m
m m m m m m m b a ++++--+-==⨯=-
,又
99111511m m m m +
=++-≥-=++(当且仅当2m =时取等号),所以b a 的最
小值为5
232.=
10.-6
【解析】先画出二元一次不等式组所表示的平面区域,令0z =,画出基准线12
y x =-
,
在可行域上平移基准线,当直线的截距最小时,找到最优解为直线9x y -=和23x y +=的交点,解出两直线交点坐标为(4,-5),得出线性目标函数的最小值
242(5)6z x y =+=+⨯-=-;
11.(1)x ∈(∪).(2)见解析
【解析】(1)解:x ∈(∪). (2)证明:对任意两个不相等的正数a 、b ,有
a 3
+b 3
a 2
b +ab 2
因为|a 3
+b 3
-2ab
|-|a 2b +ab 2-2ab |=(a +b)(a -b)2>0,所以|a 3+b 3-
2
b +ab 2
-
①当4
1
≤
λ时,16492)41()(min +-==λg t g , (8分)
令116492=+
-λ,得4
1
833>=λ,不符合舍去; (9分)
②当
24
1
≤<λ时,3)()(2min +-==λλg t g , (10分) 令132=+-λ,得2=λ,或4
1
2<-=λ,不符合舍去; (11分)
③当2>λ时,74)2()(min +-==λg t g , (12分) 令174=+-λ,得22
3
<=
λ,不符合舍去. (13分) 综上所述,实数λ的值为2. (14分)。