信号与系统第1章习题

信号系统(第3版)习题解答《信号与系统》（第3版）习题解析高等教育出版社目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(c) (d)题1-1图解 (a)、(c)、(d)为连续信号；(b)为离散信号；(d)为周期信号；其余为非周期信号；(a)、(b)、(c)为有始（因果）信号。

1-2 给定题1-2图示信号f ( t )，试画出下列信号的波形。

[提示：f ( 2t )表示将f ( t )波形压缩，f (2t )表示将f ( t )波形展宽。

] (a) 2 f ( t - 2 )(b) f ( 2t )(c) f ( 2t ) (d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。

图p1-21-3 如图1-3图示，R 、L 、C 元件可以看成以电流为输入，电压为响应的简单线性系统S R 、S L 、S C ，试写出各系统响应电压与激励电流函数关系的表达式。

题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i L t u L L d )(d )(= ⎰∞-=t C C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。

S R S L S C题1-4图解 系统为反馈联接形式。

设加法器的输出为x ( t )，由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有 )()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|，试判定该系统是否为线性时不变系统？解 设T 为系统的运算子，则可以表示为)()]([)(t f t f T t y ==不失一般性，设f ( t ) = f 1( t ) + f 2( t )，则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性，故为非线性时不变系统。

第一章绪论1、选择题1.1、f （5-2t ）是如下运算的结果 CA 、 f （-2t ）右移5B 、 f （-2t ）左移5C 、 f （-2t ）右移25D 、 f （-2t ）左移25 1.2、f （t 0-a t ）是如下运算的结果 C 。

A 、f （-a t ）右移t 0；B 、f （-a t ）左移t 0 ；C 、f （-a t ）右移a t 0；D 、f （-a t ）左移at 0 1.3、已知 系统的激励e(t)与响应r(t)的关系为：)()()(t u t e t r = 则该系统为 B 。

A 、线性时不变系统；B 、线性时变系统；C 、非线性时不变系统；D 、非线性时变系统 1.4、已知 系统的激励e(t)与响应r(t)的关系为：)()(2t e t r = 则该系统为 C 。

A 、线性时不变系统 B 、线性时变系统 C 、非线性时不变系统 D 、非线性时变系统 1.5、已知 系统的激励e(t)与响应r(t)的关系为：)1()(t e t r -= 则该系统为 B 。

A 、线性时不变系统B 、线性时变系统C 、非线性时不变系统D 、非线性时变系统1.6、已知 系统的激励e(t)与响应r(t)的关系为：)2()(t e t r = 则该系统为 B A 、线性时不变系统 B 、线性时变系统 C 、非线性时不变系统 D 、非线性时变系统 1.7.信号)34cos(3)(π+=t t x 的周期为 C 。

A 、π2 B 、π C 、2π D 、π21.8、信号)30cos()10cos(2)(t t t f -=的周期为： B 。

A 、15π B 、5π C 、π D 、10π1.9、dt t t )2(2cos 33+⎰-δπ等于 B 。

A.0 B.-1 C.2 D.-21.10、 若)(t x 是己录制声音的磁带,则下列表述错误的是： BA. )(t x -表示将此磁带倒转播放产生的信号B. )2(t x 表示将此磁带放音速度降低一半播放C. )(0t t x -表示将此磁带延迟0t 时间播放D. )(2t x 表示将磁带的音量放大一倍播放 1.11.=⋅)]([cos t u t dtdA A ．)()(sin t t u t δ+⋅- B. t sin - C. )(t δ D.t cos1.12．信号t t t x o 2cos 4)304cos(3)(++=的周期为 B 。

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD （15,6）=3 Hz 。

因此，公共周期3110==f T s 。

(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD （5, 15）=5 Hz 。

因此，公共周期5110==f T s 。

(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数，因此无法找出公共周期。

所以是非周期的。

(d) 两个分量是同频率的，基频 =0f 1/π Hz 。

因此，公共周期π==01f T s 。

1-2 解 (a) 波形如图1-2(a)所示。

显然是功率信号。

t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。

显然是能量信号。

3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号，显然有 1=P W1-3 解 周期T=7 ，一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+； (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。

1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。

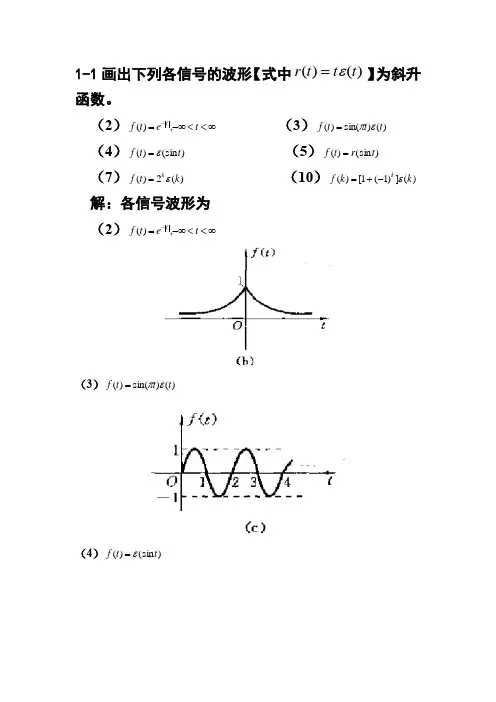
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为 （2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)(sin )(t t f ε=（5）)f=rt)(sin(t（7）)t=(kf kε(2)（10）)f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k ---=εε解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

如果是，确定其周期。

（2）)63cos()443cos()(2ππππ+++=k k k f（5）)sin(2cos 3)(5t t t f π+=解：1-6 已知信号)(t f 的波形如图1-5所示，画出下列各函数的波形。

第1章 习题答案1－1 题1－1图所示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？解： ① 连续信号：图〔a 〕、〔c 〕、〔d 〕； ② 离散信号：图〔b 〕； ③ 周期信号：图〔d 〕； ④ 非周期信号：图〔a 〕、〔b 〕、〔c 〕； ⑤有始信号：图〔a 〕、〔b 〕、〔c 〕。

1－2 某系统的输入f(t)与输出y(t)的关系为y(t)=|f(t)|，试判定该系统是否为线性时不变系统。

解： 设T 为此系统的运算子，由条件可知： y(t)=T[f(t)]=|f(t)|，以下分别判定此系统的线性和时不变性。

① 线性1〕可加性不失一般性，设f(t)=f 1(t)+f 2(t)，那么y 1(t)=T[f 1(t)]=|f 1(t)|，y 2(t)=T[f 2(t)]=|f 2(t)|，y(t)=T[f(t)]=T[f 1(t)+f 2(t)]=|f 1(t)+f 2(t)|，而|f 1(t)|＋|f 2(t)|≠|f 1(t)+f 2(t)|即在f 1(t)→y 1(t)、f 2(t)→y 2(t)前提下，不存在f 1(t)＋f 2(t)→y 1(t)＋y 2(t)，因此系统不具备可加性。

由此，即足以判定此系统为一非线性系统，而不需在判定系统是否具备齐次性特性。

2〕齐次性由条件，y(t)=T[f(t)]=|f(t)|，那么T[af(t)]=|af(t)|≠a|f(t)|=ay(t) 〔其中a 为任一常数〕即在f(t)→y(t)前提下，不存在af(t)→ay(t),此系统不具备齐次性，由此亦可判定此系统为一非线性系统。

② 时不变特性由条件y(t)=T[f(t)]=|f(t)|，那么y(t-t 0)=T[f(t-t 0)]=|f(t-t 0)|，即由f(t)→y(t)，可推出f(t-t 0)→y(t-t 0)，因此，此系统具备时不变特性。

依据上述①、②两点，可判定此系统为一非线性时不变系统。

一、填空题1．信号()f t 在区间a t a −<<上的功率可表示为 。

2．信号(4)f t −−可将信号()f t ，得到(4)f t −；而后 ，得到(4)f t −−。

3．连续系统的时域框图的基本单元包括积分器、加法器、 和 。

4．单位冲激函数的积分运算可以得到 ；单位阶跃函数的 微分运算可以得到 。

5．根据系统初始状态和激励的不同影响，LTI 连续系统的响应可分为 和 。

6．离散系统可用 方程来描述。

7．LTI 连续系统的零输入响应与 之和可构成LTI 系统的 。

8．时间上是离散的、幅度上是量化的信号称做__________。

二、单项选择题（在每小题的备选答案中，选出一个正确答案，并将正确答案的序号填在括号内。

）1．单位序列在k=（ ）时其数值为1。

A ．1 B ．0 C ．无穷大 D ．无穷小2．已知某连续系统的零状态响应()2()zs y t f t =，则可知系统是（ ）。

A ．不能确定稳定性 B ．稳定的 C ．不稳定的 D ．非因果的3．根据冲激函数的性质，()ate t δ可化简为（ ）。

A ．0B ．1C ．()t δD ．∞4．在LTI 系统中，已知激励信号为()f t 时的零状态响应为()zs y t ，则可知系统在激励信号为(5)f t −时的零状态响应为（ ）。

A ．不能确定B ．()zs y tC ．(5)zs y t −D ．1(1)8zs y t −三．判断题 （下述结论若正确，则在括号内填入√，若错误则填入×）1、离散信号和数字信号的含义相同。

（ ） 2．单位阶跃序列在k=0时取值为1。

（ ）四、画图题1、画出LTI 离散时间系统 )1()1(3)(−=−+k f k y k y 的系统框图。

2．已知信号()f t 的波形如图所示，试画出()(1)(1)g t f t t ε=−−的波形图。

3．已知信号()f t 的波形如图所示，试画出d ()d f t t的波形图。

《信号与系统》自测题第1章 信号与系统的概念一、填空题1、描述信号的基本方法有 数学表达式 、 波形 。

2、()Sa t 信号又称为 抽样信号或取样信号 。

3、()du t dt=()t δ。

4、()t δ-=()t δ（用单位冲激函数表示）。

5、对于一个自变量无穷但能量有限的信号，其平均功率为0。

6、对于下图示波形可用单位阶跃函数表示为()(1)(2)3(3)u t u t u t u t +-+---。

7、2(321)(1)t t t dt δ∞-∞++-=⎰6 。

8、525(32)(1)t t t dt δ--+-=⎰ 0 。

9、00()(2)t t u t t dt δ∞-∞--=⎰ 0 （已知00t >）。

10、0()(2)3t d τδττ--=⎰ -6 。

11、0sin()[(1)(1)]2t t t dt πδδ-∞-++=⎰ 1 。

12、0sin()(1)2t t dt πδ∞-=⎰ 1 。

13、系统的数学描述方法有 输入输出描述法 和 状态变量描述法 。

14、满足 齐次性 和 可加性或叠加性 条件的系统称为线性系统。

15、若某系统是时不变的，则当()()f f t y t −−−→系统，应有()d f t t -−−−→系统()d y t t -。

16、系统对()f t 的响应为()y t ，若系统对0()f t t -的响应为0()y t t -，则该系统为 时不变 系统。

17、连续系统模拟中常用的理想运算器有 加法器 、 数乘器 、 乘法器 、 延时器 和 积分器 。

18、离散系统模拟中常用的理想运算器有 加法器 、 数乘器 、 乘法器 和 延时器 。

二、单项选择题1、连续时间信号2()[5sin(8)]f t t =的周期是（ C ）。

A 、π B 、4πC 、8πD 、2π注：sin(8)t 的周期为4π，而2()[5sin(8)]f t t =的周期为8π。

1-1 分别判断图1-1所示各波形是连续时间信号还是离散时间信号，若是离散时间信号是否为数字信号？图1-1图1-2解 信号分类如下：⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--））（散（例见图数字：幅值、时间均离））（连续（例见图抽样：时间离散，幅值离散））（连续（例见图量化：幅值离散，时间））（续（例见图模拟：幅值、时间均连连续信号d 21c 21b 21a 21图1-1所示信号分别为 （a ）连续信号（模拟信号）； （b ）连续（量化）信号； （c ）离散信号，数字信号； （d ）离散信号；（e ）离散信号，数字信号； （f ）离散信号，数字信号。

1-2 分别判断下列各函数式属于何种信号？（重复1-1题所示问） （1）)sin(t e at ω-； （2）nT e -； （3）)cos(πn ；（4）为任意值）（00)sin(ωωn ；（5）221⎪⎭⎫⎝⎛。

解由1-1题的分析可知： （1）连续信号； （2）离散信号；（3）离散信号，数字信号； （4）离散信号； （5）离散信号。

1-3 分别求下列各周期信号的周期T ： （1）)30t (cos )10t (cos -； （2）j10t e ；（3）2)]8t (5sin [；（4）[]为整数）（n )T nT t (u )nT t (u )1(0n n ∑∞=-----。

解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号，需要考察各分量信号的周期是否存在公倍数，若存在，则该复合信号的周期极为此公倍数；若不存在，则该复合信号为非周期信号。

（1）对于分量cos (10t )其周期5T 1π=；对于分量cos (30t )，其周期15T 2π=。

由于5π为21T T 、的最小公倍数，所以此信号的周期5T π=。

（2）由欧拉公式)t (jsin )t (cos e t j ωωω+= 即)10t (jsin )10t (cos e j10t +=得周期5102T ππ==。

信号与系统第三版课后习题答案信号与系统第三版课后习题答案信号与系统是电子信息类专业中一门重要的基础课程，它是研究信号的产生、传输、处理和识别的学科。

在学习这门课程时，课后习题是非常重要的，它可以帮助我们巩固所学的知识，并且提高解决问题的能力。

下面是信号与系统第三版课后习题的答案。

第一章：信号与系统的基本概念1. 信号是指随时间、空间或其他独立变量的变化而变化的物理量。

系统是指能够对输入信号进行处理并产生输出信号的物理设备或数学模型。

2. 连续时间信号是在连续时间范围内定义的信号，可以用连续函数表示。

离散时间信号是在离散时间范围内定义的信号，可以用数列表示。

3. 周期信号是指在一定时间间隔内重复出现的信号，具有周期性。

非周期信号是指不具有周期性的信号。

4. 奇对称信号是指关于原点对称的信号，即f(t)=-f(-t)。

偶对称信号是指关于原点对称的信号，即f(t)=f(-t)。

5. 系统的线性性质是指系统满足叠加原理，即对于输入信号的线性组合，输出信号也是这些输入信号的线性组合。

6. 系统的时不变性质是指系统对于不同时间的输入信号，输出信号的特性是不变的。

7. 系统的因果性质是指系统的输出只依赖于当前和过去的输入信号，而不依赖于未来的输入信号。

第二章：连续时间信号与系统的时域分析1. 奇偶分解是将一个信号分解为奇对称和偶对称两个部分的过程。

奇偶分解的目的是简化信号的处理和分析。

2. 卷积是信号处理中常用的一种操作，它描述了两个信号之间的相互作用。

卷积的定义为：y(t) = ∫[x(τ)h(t-τ)]dτ。

3. 系统的冲激响应是指系统对于单位冲激信号的输出响应。

冲激响应可以用来描述系统的特性和性能。

4. 系统的单位阶跃响应是指系统对于单位阶跃信号的输出响应。

单位阶跃响应可以用来描述系统的稳定性和响应速度。

5. 系统的单位斜坡响应是指系统对于单位斜坡信号的输出响应。

单位斜坡响应可以用来描述系统的积分特性。

1-4 分析过程：（1）例1-1的方法：()()()()23232f t f t f t f t →−→−→−− （2）方法二：()()()233323f t f t f t f t ⎡⎤⎛⎞→→−→−−⎜⎟⎢⎥⎝⎠⎣⎦（3）方法三：()()()()232f t f t f t f t →−→−+→−−⎡⎤⎣⎦ 解题过程：（1）方法一：方法二：（1）()−f at 左移0t ：()()()000−+=−−≠−⎡⎤⎣⎦f a t t f at at f t at （2）()f at 右移0t ：()()()000−=−≠−⎡⎤⎣⎦f a t t f at at f t at （3）()f at 左移0t a ：()()000⎡⎤⎛⎞+=+≠−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a （4）()f at 右移0t a ：()()000⎡⎤⎛⎞−−=−+=−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a 故（4）运算可以得到正确结果。

注：1-4、1-5题考察信号时域运算：1-4题说明采用不同的运算次序可以得到一致的结果；1-5题提醒所有的运算是针对自变量t 进行的。

如果先进行尺度变换或者反转变换，再进行移位变换，一定要注意移位量和移位的方向。

1-9 解题过程： （1）()()()2tf t eu t −=− （2）()()()232tt f t ee u t −−=+（3）()()()255ttf t e eu t −−=− （4）()()()()cos 1012tf t et u t u t π−=−−−⎡⎤⎣⎦1-12 解题过程：（（（（注：1-9、1-12题中的时域信号均为实因果信号，即()()()=f t f t u t 1-18 分析过程：任何信号均可分解为奇分量与偶分量之和的形式，即()()()()1e o f t f t f t =+其中，()e f t 为偶分量，()o f t 为奇分量，二者性质如下：()()()()()()23e e o o f t f t f t f t =−=−−()()13∼式联立得()()()12e f t f t f t =+−⎡⎤⎣⎦ ()()()12o f t f t f t =−−⎡⎤⎣⎦ 解题过程：(a-1) (a-2)(a-3)(a-4)f t为偶函数，故只有偶分量，为其本身(b) ()(c-1)(c-2)(c-3)(c-4)(d-1)(d-2)(d-3)(d-4)1-20 分析过程：本题为判断系统性质：线性、时不变性、因果性（1）线性（Linearity）：基本含义为叠加性和均匀性即输入()1x t ，()2x t 得到的输出分别为()1y t ，()2y t ，()()11T x t y t =⎡⎤⎣⎦，()()22T x t y t =⎡⎤⎣⎦，则()()()()11221122T c x t c x t c y t c y t +=+⎡⎤⎣⎦（1c ，2c 为常数）。

第1章 习 题 解 答1-1．判断下列信号是否是周期性的，如果是周期性的，试确定其基波周期（1）()⎪⎭⎫⎝⎛+=43cos 2πt t f 解：对于()k Z ∈()222cos 32cos 322cos 333444f t k t k t k t f t ππππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+=++=++=+= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭∴原函数是周期函数，令1k =，则基波周期为23π。

（2）()26sin ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=πt t f解：对于()k Z ∈()()22sin sin 66f t k t k t f t ππππ⎡⎤⎡⎤⎛⎫⎛⎫+=+-=-= ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦∴原函数是周期函数，令1k =，则基波周期为π。

（3）()[]()t u t t f π2cos =解：设其存在周期，令周期为T()()()cos 2f t T t T u t T π+=++⎡⎤⎣⎦在0T ≠的情况下函数不为零的部分发生了平移，故()()f t T f t +≠∴原函数不是周期函数。

（4）())(42π+=t j et f解：对于()k Z ∈())()(())(()224442222j t k j t j t j k f t k eeeef t ππππππ+++++==⨯==∴原函数是周期函数，令1k =，则基波周期为2π。

1-2．求信号())14sin()110cos(2--+=t t t f 的基波周期。

解：cos(101)t +的基波周期为15π， s i n (41)t -的基波周期为12π二者的最小公倍数为π，故())14sin()110cos(2--+=t t t f 的基波周期为π。

1-3．设()3,0<=t t f , 对以下每个信号确定其值一定为零的t 值区间。

（1）()t f -1 （2）()()t f t f -+-21 （3）)()(t f t f --21 （4）()t f 3 （5）()3tf解：（1）()t f -1为()f t 反折后向右平移一个单位得到，故当()2t >-时()10f t -=（2）()2f t -为()f t 反折后向右平移两个单位得到，故当()1t >-时()20f t -=。