机械原理 瞬心例题

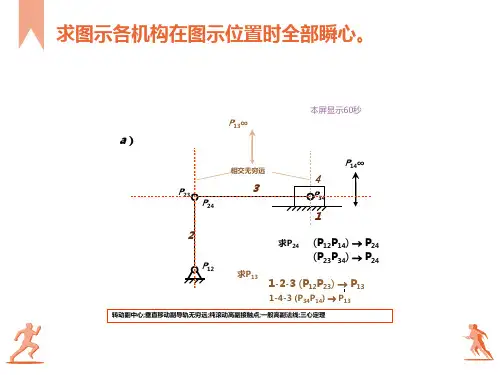
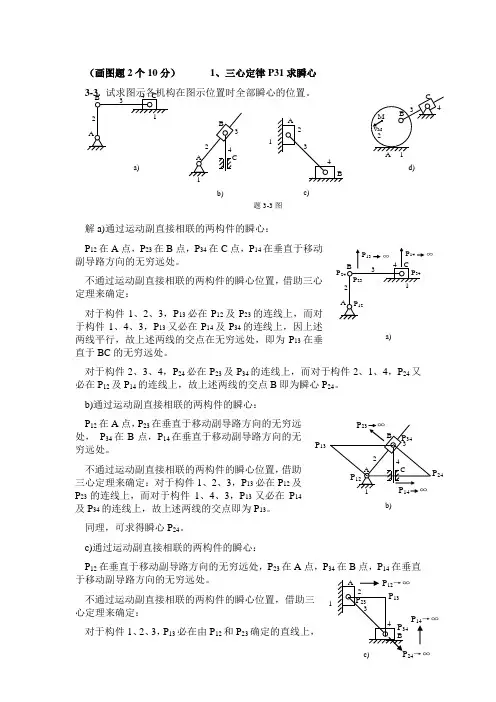
（画图题2个10分） 1、三心定律P31求瞬心解a)通过运动副直接相联的两构件的瞬心：P 12在A 点，P 23在B 点，P 34在C 点，P 14在垂直于移动副导路方向的无穷远处。

不通过运动副直接相联的两构件的瞬心位置，借助三心定理来确定：对于构件1、2、3，P 13必在P 12及P 23的连线上，而对于构件1、4、3，P 13又必在P 14及P 34的连线上，因上述两线平行，故上述两线的交点在无穷远处，即为P 13在垂直于BC 的无穷远处。

对于构件2、3、4，P 24必在P 23及P 34的连线上，而对于构件2、1、4，P 24又必在P 12及P 14的连线上，故上述两线的交点B 即为瞬心P 24。

b)通过运动副直接相联的两构件的瞬心： P 12在A 点，P 23在垂直于移动副导路方向的无穷远处， P 34在B 点，P 14在垂直于移动副导路方向的无穷远处。

不通过运动副直接相联的两构件的瞬心位置，借助三心定理来确定：对于构件1、2、3，P 13必在P 12及P 23的连线上，而对于构件1、4、3，P 13又必在P 14及P 34的连线上，故上述两线的交点即为P 13。

同理，可求得瞬心P 24。

c)通过运动副直接相联的两构件的瞬心：P 12在垂直于移动副导路方向的无穷远处，P 23在A 点，P 34在B 点，P 14在垂直于移动副导路方向的无穷远处。

不通过运动副直接相联的两构件的瞬心位置，借助三心定理来确定：对于构件1、2、3，P 13必在由P 12和P 23确定的直线上，a)b)d) 题3-3图a)b)P 13P 24 AB1234 c)1P 14→∞24→∞而对于构件1、4、3，P 13又必在由P 14和P 34确定的直线上，故上述两直线的交点即为P 13。

对于构件2、3、4，P 24必在由P 23和P 34确定的直线上，而对于构件2、1、4，P 24又必在由P 12及P 14确定的直线上（两个无穷远点确定的直线），故上述两线的交点即为P 24，即P 24在直线AB 上的无穷远处。

机械原理瞬心法求速度习题引言机械原理是工程力学的一部分，研究物体的运动及力学效应。

在机械原理中，瞬心法是一种常用的分析方法，用于求解物体的速度和加速度。

本文将通过解答一些瞬心法求速度的习题，加深对机械原理的理解。

问题一有一个直径为1m的转盘，上面有一个固定在轴上的活动滑块。

滑块到轴的距离为0.5m。

转盘以5 rad/s的角速度逆时针旋转。

求滑块上某点P的速度。

首先，我们需要确定滑块上的点P的位置。

由于滑块到轴的距离为0.5m，而转盘的直径为1m，因此点P的位置位于滑块上与轴对称的位置，距离轴0.5m。

我们可以使用瞬心法来求解滑块上点P的速度。

瞬心法的基本原理是，在运动过程中，物体的速度等于通过瞬时转动中心与物体上的某一点所作的相对速度。

在本题中，我们可以选择转盘的轴作为瞬时转动中心。

因此，我们需要确定点P相对于转动中心的位置向量和其相对于转动中心的速度向量。

点P相对于转动中心的位置向量为[0.5, 0]，即P的横坐标为0.5m，纵坐标为0，代表距离转动中心0.5m。

点P相对于转动中心的速度向量为[0, R * ω]，其中R 为转盘的半径，即0.5m，ω为转盘的角速度，即5 rad/s。

代入数值计算，得到速度向量为[0, 2.5]，即P点的速度大小为2.5 m/s，方向为垂直于转盘的切线方向。

问题二一个直径为0.8m的小车以2 rad/s的角速度逆时针旋转。

小车上有一根长1.2m的杆，杆上距离小车中心0.6m处有一个质量为1kg的小球。

求小球的速度大小和方向。

我们可以使用瞬心法来求解小球的速度。

同样地，选择小车的中心作为瞬时转动中心。

首先，我们需要确定小球相对于转动中心的位置向量和其相对于转动中心的速度向量。

小球相对于转动中心的位置向量为[0.6, 0]，即小球距离转动中心0.6m。

小球相对于转动中心的速度向量为[0, R * ω]，其中R为小车直径的一半，即0.4m，ω为小车的角速度，即2 rad/s。

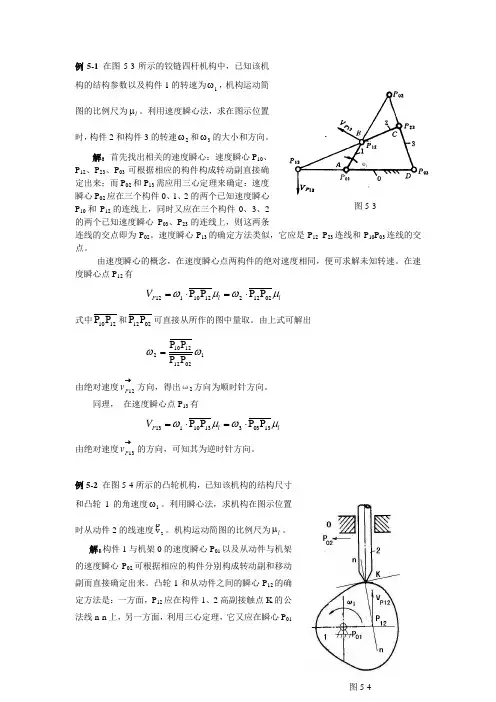
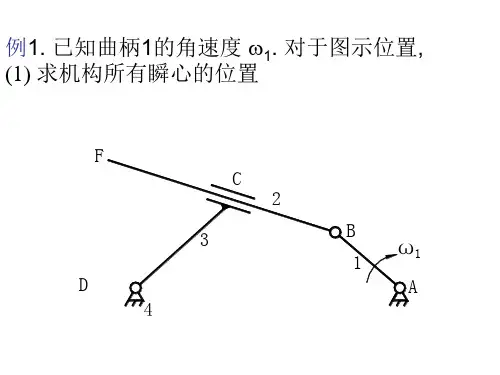
例5-1 在图5-3所示的铰链四杆机构中，已知该机构的结构参数以及构件1的转速为1ω，机构运动简图的比例尺为l μ。

利用速度瞬心法，求在图示位置时，构件2和构件3的转速2ω和3ω的大小和方向。

解：首先找出相关的速度瞬心：速度瞬心P 10、P 12、P 23、P 03可根据相应的构件构成转动副直接确定出来；而P 02和P 13需应用三心定理来确定：速度瞬心P 02应在三个构件0、1、2的两个已知速度瞬心P 10和P 12的连线上，同时又应在三个构件0、3、2的两个已知速度瞬心P 03、P 23的连线上，则这两条连线的交点即为P 02。

速度瞬心P 13的确定方法类似，它应是P 12 P 23连线和P 10P 03连线的交点。

由速度瞬心的概念，在速度瞬心点两构件的绝对速度相同，便可求解未知转速。

在速度瞬心点P 12有l l P V μωμω021*********P P P P ⋅=⋅= 式中1210P P 和0212P P 可直接从所作的图中量取。

由上式可解出1021212102P P P P ωω=由绝对速度→12P v 方向，得出ω2方向为顺时针方向。

同理， 在速度瞬心点P 13有l l P V μωμω130331310113P P P P ⋅=⋅= 由绝对速度→13P v 的方向，可知其为逆时针方向。

例5-2 在图5-4所示的凸轮机构，已知该机构的结构尺寸和凸轮1的角速度1ω。

利用瞬心法，求机构在图示位置时从动件2的线速度2v。

机构运动简图的比例尺为l μ。

解：构件1与机架0的速度瞬心P 01以及从动件与机架的速度瞬心P 02可根据相应的构件分别构成转动副和移动副而直接确定出来。

凸轮1和从动件之间的瞬心P 12的确定方法是：一方面，P 12应在构件1、2高副接触点K 的公法线n-n 上，另一方面，利用三心定理，它又应在瞬心P 01图5-4图5-3和P 02的连线上，即又应在过点P 01而垂直于从动件2与机架移动副导路的直线上。

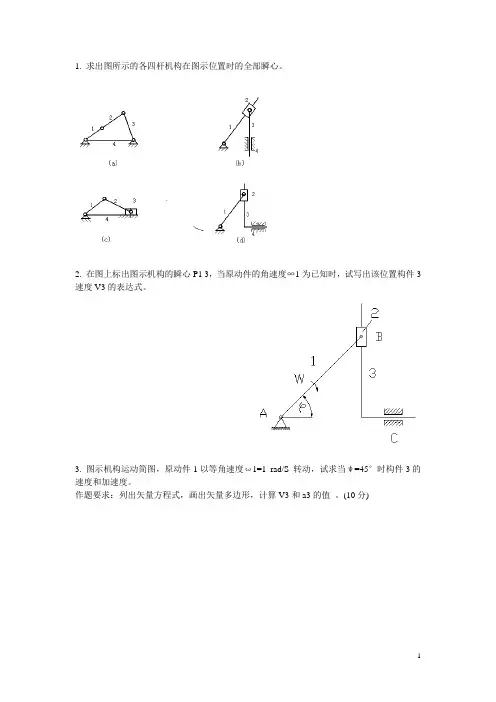
1. 求出图所示的各四杆机构在图示位置时的全部瞬心。

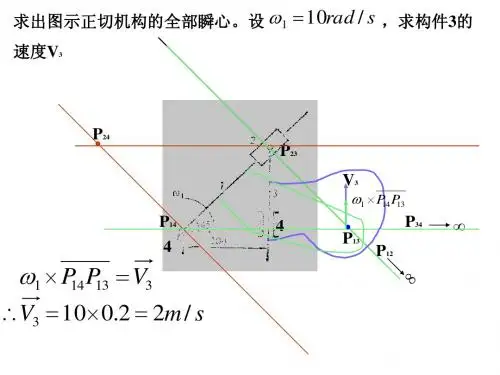
2. 在图上标出图示机构的瞬心P1 3，当原动件的角速度∞1为已知时，试写出该位置构件3速度V3的表达式。

3. 图示机构运动简图，原动件1以等角速度ω1=1 rad/S 转动，试求当ψ=45°时构件3的速度和加速度。

作题要求：列出矢量方程式，画出矢量多边形，计算V3和a3的值。

(10分)2题图3. 图示导杆机构的运动简图及速度多边形，已知原动件1以ω1=20rad/s逆时针等速转动，按下列要求作加速度分析：a的加速矢量方程式；1．写出求3Bp已画在图中）；2．画加速度多边形（''b3．计算构件3 的角加速度ε3的值，并将其方向标在图上。

4. 图示干草压缩机的机构运动简图（比例尺为μl）。

原动件曲柄1以等角速度ω1转动，试用矢量方程图解法求该位置活塞5的速度与加速度。

要求：1．写出C、E点速度与加速度的矢量方程式；2．画出速度与加速度矢量多边形（大小不按比例尺，但其方向与图对应）；3．据矢量多边形写出计算E点的速度V E与加速度a E的表达式。

（10分）5. 在图示机构中，原动件1以等角速度ω1转动。

试作： 1．写出B 3点的速度，加速度矢量方程式；2．在图上分别由Pb1表示（1B V ）、P ′b1′（表示2B a ）开始，画出速度，加速度多边形（法向加速度和哥氏加速度的工度任取）；3．写出构件3的角速度ω3、角加速度∝3的表达式。

6. 图示为转动导杆机构的运动简图，速度矢量图以及表示B 1点加速度的矢量1''b P 。

试作： 1．求角速度ω3的大小并指出方向；2．求相对速度V B3B2的大小并指出方向； 3．写出3B a 的矢量方向式； 4．完成加速度矢量图。

7. 图示铰链四杆机构，已知各杆尺寸及原动件角速度ω1。

试作：1b 2b 3b '1bm ms m a 2/01.0=μmmml 01.0=μm msm v /01.0=μ1ωϕ①写出点C 的速度V C 及加速度C a 的矢量方程式； ②画出速度矢量多边形（其大小随意，但方向必须正确）；8. 图示为机构运动简图及其相应的速度矢量图，用图中线段和比例尺符号写出哥氏加速度a k a4a3的表达式，并指出方向。

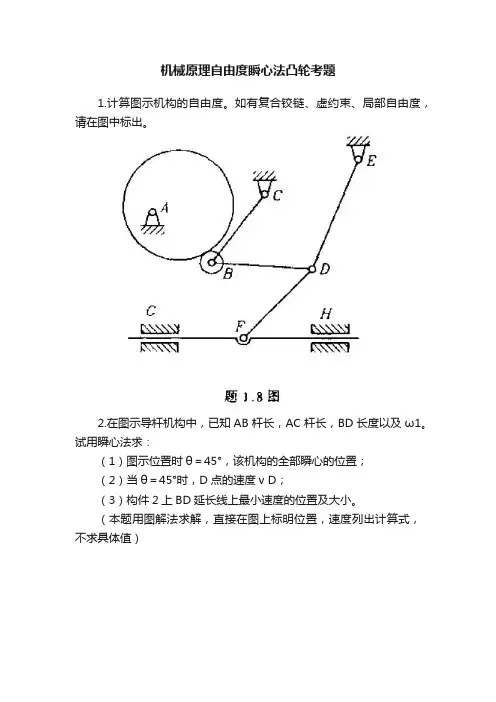
机械原理自由度瞬心法凸轮考题1.计算图示机构的自由度。

如有复合铰链、虚约束、局部自由度，请在图中标出。

2.在图示导杆机构中，已知AB杆长，AC杆长，BD长度以及ω1。

试用瞬心法求：（1）图示位置时θ＝45°，该机构的全部瞬心的位置；（2）当θ＝45°时，D点的速度v D；（3）构件2上BD延长线上最小速度的位置及大小。

（本题用图解法求解，直接在图上标明位置，速度列出计算式，不求具体值）3.图示为一偏置式滚子推杆盘状凸轮机构，凸轮为一偏心圆，逆时针回转，其直径D＝32mm，滚子半径为r＝5mm，偏距e＝6mm，试根据图示位置1）画出凸轮的理论廓线、偏距圆；2）求出基圆半径rb、最大行程h、升程角δ0；3）画出图示位置时凸轮的压力角。

答案：1.2.（1）共有6个瞬心，如图所示；（2）vD＝ω1·DF（3）最小速度点位置为E点，如图所示vE＝ω1·EF3.1.计算下图机构自由度（若机构中存在复合铰链、局部自由度或虚约束，请明确指出）。

2.图示机构运动简图中，设已知各构件的尺寸及原动件1的速度v1和加速度a1，现要求：（1）确定图示位置时该机构全部瞬心的位置；（2）用瞬心法求构件2及构件3的瞬时角速度ω2、ω3（列出计算式，不求具体值）；（3）求构件2上瞬时速度为零的点的位置（在图上标出）。

G A B E FC D3.图示为一偏心圆凸轮机构，O 为偏心圆的转动中心，C 为几何中心。

（1）画出凸轮的理论廓线并求出凸轮的基圆半径r b ；（2）用作图法求从动件2的最大升程h 和推程运动角δ1；（3）在图中标出凸轮从图示位置转过90时从动件的位移s 与机构的压力角α。

答案：1.6,8,1L h n P P ===（2′）机构自由度：323628111L h F n P P =--=?-?-?=（1′）2.3.。

第2章习题2-1 求出图2-12所示机构中所有速度瞬心。

2-2 在图2-13所示的凸轮机构中，已知r=50mm，l OA=22mm，l AC=80mm,ψ1=90°，凸轮1的角速度ω1=10 ，逆时针转动。

试用瞬心法求从动件2的角速度ω2 。

2-3 图2-14所示四铰链运动链中，已知名构件长度l AB=55mm，l BC=40mm，l CD=50mm，l AD=25mm。

试问：（1）该运动链中是否具有双整转副构件？（2）如果具有双整转副构件，则固定哪个构件可获得曲柄摇杆机构?（3）固定哪个构件可获得双曲柄机构？（4）固定哪个构件可获得双摇杆机构？2-4 在图2-15所示的铰链四杆机构中，各杆件长度分别为l AB=28mm，l BC=52mm，l CD=50mm，l AD=72mm。

（1）若取AD为机架，求该机构的极位夹角θ，杆CD的摆角ψ和最小传动角γmin。

（2）若取AB为机架，该机构将演化为何种类型的机构？为什么？清说明这时C、D 两个转动副是整转还是摆动副？2-5 在图2-16所示机构中，已知l AB=100mm，l BC=l CD=400mm，l EF=200mm，∠BCD=90°，∠CFE=30°，ω1=100rad/s。

试求角速度ω5、速度νE4，角加速度ε5和加速度αE4。

2-6 在图2-17所示的摆动导杆机构中，∠BAC=90°，l AB60mm，l AC=120mm，曲柄AB的等角速度ω1=30rad/s。

求构件3的角速度ω3和角加速度ε3。

2-7 在图2-18所示的曲柄摇块机构中，已知l AB=30mm，l AC=100mm，l BD=50mm，ϕ=45°，等角速度ω1=10rad/s。

求点E、D的速度和加速度，构件3的角速度l DE=40mm，1ω3和角加速度ε3。

ϕ=45°，ω1=100rad/s，方向为逆时针方向，l AB=4m，2-8 在图2-19所示的机构中，已知1γ=60°。

1.在图示机构中，已知φ=45°，H=50mm，ω1=100rad/s。

试用瞬心法确定图示位置构件
3的瞬时速度v3的大小及方向。

2.在图示机构中已知凸轮以ω2的角速度顺时针方向转动，试用瞬心法求出从动件3的速
度(用图及表达式表示)。

3、在图示的轮系中，已知齿轮1的转速n1=120r/min，转向如图所示，而且z1=40，z2=20，求：(1)z3=? (2)n3=0时，齿轮2的转速n2=? (大小和转向)
题六图
4、某机器的主轴平均角速度ωm=100rad/s，机器运转的速度不均匀系数δ=0.05，求该机器
的最大角速度ωmax，最小角速度ωmin。

5、图示机构中，各摩擦面间的摩擦角均为φ,Q为生产阻力，P为驱动力。

试在图中画出各运动副的总反力：R32，R12，R31（包括作用线位置与指向）。

6、图示偏置直动滚子从动件盘形凸轮机构中，凸轮以角速度ω逆时针方向转动。

试在图上：
(1)画出理论轮廓曲线、基圆与偏距圆；
(2)标出凸轮从图示位置转过45°时的压力角α和位移s 。

7、在图示双滑块机构中，滑块1在驱动力P 作用下等速运动。

移动副中的滑动摩擦系数f =0.176327，l AB =200mm 。

若不计各转动副中的摩擦和各构件的重量。

当P =500N 时，试求所能克服的生产阻力Q 以及该机构在此瞬时位置的效率。

（10分） 30°Q
B
2
314
A P
100。

机械原理影像法例题
确定速度瞬心位置的方法:
①若两构件直接组成运动副时，可用观察法确定，即两构件组成转动副时，速度瞬心位于转动中心;组成移动副时，速度瞬心位于垂直于移动方位的无穷远处;组成平面滚滑副时，速度瞬心位于过接触点的公法线上。

②若两构件不直接组成运动副时，可借助于三心定理来确定速度瞬心的位置。

三心定理:互作平面平行运动的三个构件，共有三个瞬心，且位于同一直线上。

即三个构件的三个速度瞬心中，若已知两个瞬心的位置，则第三个瞬心一定位于该两瞬心的连线上。

③绝对瞬心与相对瞬心的判定:凡与机架组成的瞬心为绝对瞬心，否则为相对瞬心。

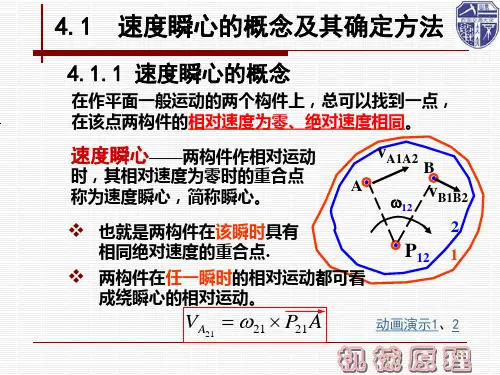
④也可由速度瞬心的定义来确定速度瞬心的位置。

例：图示铰链四杆机构，原动件2以ω2沿顺时针方向转动，求机构在图示位置时构件4的角速度ω4的大小和方向。

2 平面机构的运动分析1。

图 示 平 面 六 杆 机 构 的 速 度 多 边 形 中 矢 量 ed →代 表 ， 杆4 角 速 度ω4的 方 向 为时 针 方 向。

2。

当 两 个 构 件 组 成 移 动 副 时 ，其 瞬 心 位 于 处 。

当 两 构 件 组 成 纯 滚 动 的 高 副 时， 其 瞬 心 就 在 。

当 求 机 构 的 不 互 相 直 接 联 接 各 构 件 间 的 瞬 心 时, 可 应 用 来 求。

3。

3 个 彼 此 作 平 面 平 行 运 动 的 构 件 间 共 有 个 速 度 瞬 心， 这 几 个瞬 心 必 定 位 于 上。

含 有6 个 构 件 的 平 面 机 构， 其 速 度 瞬 心 共 有 个， 其 中 有 个 是 绝 对 瞬 心， 有 个 是 相 对 瞬 心。

4。

相 对 瞬 心 与 绝 对 瞬 心 的 相 同 点 是 ，不 同 点 是 。

5。

速 度 比 例 尺 的 定 义 是 ， 在 比 例 尺 单 位 相 同 的 条 件 下, 它 的 绝 对 值 愈 大, 绘 制 出 的 速 度 多 边 形 图 形 愈 小。

6.图 示 为 六 杆 机 构 的 机 构 运 动 简 图 及 速 度 多 边 形， 图 中 矢 量 cb →代表 ， 杆3 角 速 度ω3 的 方 向 为 时 针 方 向。

7。

机 构 瞬 心 的 数 目N 与 机 构 的 构 件 数 k 的 关 系 是 。

8.在 机 构 运 动 分 析 图 解 法 中， 影 像 原 理 只 适 用 于 .9.当 两 构 件 组 成 转 动 副 时， 其 速 度 瞬 心 在 处； 组 成 移 动 副 时， 其 速 度 瞬 心 在 处； 组 成 兼 有 相 对 滚 动 和 滑 动 的 平 面 高 副 时， 其 速 度 瞬 心 在 上。

10。

.速 度 瞬 心 是 两 刚 体 上 为 零 的 重 合 点。

11。

铰 链 四 杆 机 构 共 有 个 速 度 瞬 心,其 中 个 是 绝 对 瞬 心， 个 是 相 对 瞬 心。

、单项选择题（每小题 1 分）在下列每小题的四个备选答案中选出一个正确的答案，并将其字母标号填入题干的括号1、在两构件的相对速度瞬心处，瞬时重合点间的速度应为（A ）。

A. 两点间相对速度为零，但两点的绝对速度不等于零B. 两点间相对速度不等于零，但其中一点的绝对速度等于零C. 两点间相对速度不等于零，且两点的绝对速度也不等于零D. 两点间的相对速度和绝对速度都等于零2、两构件作相对运动时，其瞬心是指（C）的重合点。

A. 绝对速度等于零B. 绝对速度和相对速度都等于零C. 绝对速度不一定等于零，但绝对速度相等或相对速度等于零D. 相对速度不等于零3、速度瞬心是指两构件上（B ）为零的重合点。

瞬心法A. 绝对速度B. 相对速度C. 绝对速度不D. 相对速度不二、填空题（每空 1 分）1、当两构件组成转动副时，其瞬心就是转动中心位置2、当求机构中不直接组成运动副两构件间的瞬心位置时，可应用三心定理来求。

三、分析题（每小题 6 分）1、对于下列机构的图示位置：①试确定机构的所有速度瞬心位置；②若已知原动件试列出求从动件 3 运动速度w3的表达式。

1 的角速度w1 ，P13 B1 P12P14 P24P23C4D—— 4 分AP13DP13 1—— 2 分2、对于下列机构的图示位置： ①试确定机构的所有速度瞬心位置； ②若已知原动件 1 试列出求从动件 3 运动速度 w 3的表达式。

v 3 AP 13 1 —— 2 分—— 4 分①试确定机构的所有速度瞬心位置； ②若已知原动件 w 3的表达式。

4、对于下列机构的图示位置： 试列出求从动件 3 运动速度 ①试确定机构的所有速度瞬心位置；v 3的表达式。

②若已知原动件的角速度 w 1，BP 23AP 13 CP 131 0 ——2 分—— 4分的角速度 w 1，—— 4 分3 D A P P 13 1 0——2 分 DP13 3、对于下列机构的图示位置： 试列出求从动件 3 运动速度①试确定机构的所有速度瞬心位置； ②若已知原动件 的角速度 w 1，—— 4 分v 3 AP 13 1 0 —— 2 分 5、对于下列机构的图示位置： 试列出求从动件 运动速度 的角速度 w 1，P 24P 346、对于下列机构的图示位置：①试确定机构的所有速度瞬心位置；②若已知原动件1 的角速度w1 ，试列出求从动件 3 运动速度w3的表达式。