机械原理 瞬心及位置确定讲课ppt

b)
P13
求P24
(P12P14) P24 (P23P34) P24
本屏显示60秒
P34 3
2
4
P12
P14∞
P24
求P13
1
1-2-3 (P12P23) P13
1-4-3 (P34P14) P13
转动副中心;垂直移动副导轨无穷远;纯滚动高副接触点;一般高副法线;三心定理
本屏显示60秒
水平方向无穷远处有P12，通过P12作竖线连接P14
比1/ 3 。
解： 1. 绘机构运动简图 2.求瞬心P13 3.求1/ 3
1 P36 P13 3 P16 P13
求P13
1-2-3 (P12P23) P13
1-6-3 (P36P16) P13
2
P23
P12 4
P13
P36 5
ห้องสมุดไป่ตู้
3
6
转动副中心;垂直移动副导轨无穷远;纯滚动高副接触点;一般高副法线;三心定理
本屏显示60秒
求P24
(P12P14) P24
(P23P34) P24
c)
P13
M
P23
2
P12
P14
4
3
P24
求P13 1-2-3 (P12P23) P13
1
1-4-3 (P34P14) P13
转动副中心;垂直移动副导轨无穷远;纯滚动高副接触点;一般高副法线;三心定理
本屏显示60秒
在图示的齿轮-连杆组合机构中, 试用瞬心法求齿轮1和3的传动
该线与通过P23P34的斜线相交于倾斜方向无穷远点
P12∞
c)
求P24
(P12P14) P24

机械原理课件第三章
§3－2 用速度瞬心法作机构的速度分析
一、速度瞬心及其位置的确定 1、速度瞬心的定义
A
vA2A1 B
若构件2相对固定的构件1运动，可求得 瞬心P12，有：
vB1B2
P12
பைடு நூலகம்
2
v v
P1
P2
0，
vP2P1 vP2 vP1 0
1
vP1 vP2 0，但 vP2P1 vP2 vP1 0
vCvP24 2P 1P 224 L
P12
1
vC
P13
C P34
4
利用瞬心P13---构件1和3的等速重合点。
P14
构件1为机架，则vP13=0， P13为构件3的瞬时转动中心，则有
3
vC P34P13L
vD3D1P3L
§3-3 矢量方程图解法（相对运动图解法）
一、同一构件上两点间的速度和加速度
2
且为绝对瞬心。
若构件1不固定，
P12
则P12为相对瞬心。
1
§3－2 用速度瞬心法作机构的速度分析
2、瞬心数目
若机构中有N个构件，则： ∵每两个构件就有一个瞬心 ∴根据排列组合，瞬心有 ：
K N(N1) 2
P13
1 23
P12 P23
构件数 4 瞬心数 6
56
8
10 15 28
§3－2 用速度瞬心法作机构的速度分析
③另外2个用三心定理求出。
P13
P12 P23
1 2 3 P14 P34
PP2244
3 P23
P23 2
1
P13
“下标同号消去 P12 P23 法P”13在P12 P23的连线上。

2
D
2
p'(a') d'
3
c'
1
A
1
x
6
C
x
n2' b'
n t a C a B a CB a CB
方向： 沿xx 大小： ? √ √ C→ B 22lAB ⊥CB ?
用加速度影像法求出d'点 作Δb'c'd' ~ ΔBCD aD= μa p'd'
t aCB n 'c ' a 2 2 l BC l BC
课堂练习
图示机构,已知各构件尺寸和ω1，用瞬心法求v5 解题思路：
1
求３ 求v5
C D
3
E
4
A
1 2
ω1
5 6
F
利用P13
利用P35
B
机械原理 —— 平面机构的运动分析
P15
求P13
求P35
P56→∞
求P15
v5 v P15 1 P16 P15 l
P35
E P 34
3 4
1 AP13 3 DP13
2 P13 vP13 B 1 AP
1 P13P14L = 3 P13P34 L
4
P34
D
P13 P14 3 1 逆时针 P13 P34
机械原理 —— 平面机构的运动分析
3 平面高副机构
3 2 1 1 1 2 3
P23
vP12 P12 P23
P13
P12 vP12
P23
P13
取μa= aB/ p'b'作加速度图 aC= μa p'c'

一、速度瞬心及其求法
1、速度瞬心的定义
两个作平面运动构件上速度相 同的一对重合点，在某一瞬时两构 件相对于该点作相对转动 ，该点称 瞬时速度中心。求法？
相对瞬心－重合点绝对速度不为零。 绝对瞬心－重合点绝对速度为零。
安徽工程科技学院专用
A (A ) 作者：潘存2 云教1授 VA2A1
2
P21
B2(B1)
56
8
10 15 28
安徽工程科技学院专用
作者： 潘存云教授
3、机构瞬心位置的确定
（1）直接观察法 （利用定义） 适用于求通过运动副直接相联的两构件瞬心位置。
P12
1
2
P12 ∞
1
n
1
2
2
P12 t
1t 2 V12
n
（2有三个瞬 心，且它们位于同一条直线上。此法特别适用 于两构件不直接相联的场合。
如右图所示的三个构件组成的一个机构若p23不与p12p13共线同一直线而在任意一点c则c点在构件2和构件3上的绝对速度的方向不可能相3上的绝对速度的方向不可能相同即绝对速度不相等
§3－1 －３ 平面机构速度分析的瞬心法
机构速度分析的图解法有：速度 瞬心法、相对运动法、线图法。 瞬心法: 适合于简单机构的运动分析。
安徽工程科技学院专用
作者： 潘存云教授
用反证法证明：
如右图所示的三个构件组成 的一个机构，若P23不与P12、 P13共线（同一直线），而在任 意一点C，则C点在构件2和构件 3上的绝对速度的方向不可能相 同，即绝对速度不相等。二只有 C点在P12、P13连成的直线上， 才能使绝对速度的方向相同。
安徽工程科技学院专用
作者： 潘存云教授
VB2B1

已知：曲柄导杆机构，曲柄的角速度为ω1（常数） 求：导杆3的角速度 3 。
2
1 A B
例2
分
析
1
3 C
取构件3为动参考系,则构件2的运动=
构件3的牵连运动+相对于构件3的相对运动
2005---2006第一学期
1
vCB 的下角标与 bc 方向相反。
速度影像只适用同一构件，△BCD与△bcd为相
第三章
平面机构速度分析
2005---2006第一学期
第一节 速度瞬心法 进行平面机构的速度分析
2005---2006第一学期
• 一、速度瞬心的概念
Aபைடு நூலகம்
B
vA
vB
1 2
1
定义：做平面运动的两构件上其 瞬时速度相等的重合点Pij 。
P 12
2
分类： 绝对速度瞬心：速度瞬心的绝对速度为零。 相对速度瞬心：速度瞬心的绝对速度不为零。
2005---2006第一学期
利用两构件同速点求解。
求构件上速度为零的点
全部同速点中，凡是其右下角数码中含有 固定件的，其速度均为零，因此k个构件组成 的机构中，速度为零的点共有k-1个。
2005---2006第一学期
第二节 用相对运动图解 法作平面机构的速度分析
2005---2006第一学期
理论基础:理论力学的刚体平面运动和点的复合运动。
N ( N 1) 2
3
瞬心数目：构件数为K，组成的瞬心数为K，K =
2005---2006第一学期
• 二、瞬心位置的确定
直接成副的瞬心位置
1
两构件构成转动副——铰链回转中心
2005---2006第一学期

α3
=
a
t CB
l BC
= n ′3 c ′μ a BC μ l
α4
=
a
t CD
l CD
= n 4′ c ′μ a CD μ l
3. 加速度分析（续） e3(e5)
(4) 求aE6和α6
A
2 B
ω2
ω 3
a3
x 5
n4'
c' n6'
n3' b'
p' (a'、d'、f ')
e6 b
c D ω4
3
C
α4
ω 2 = P14 P 24
3
ω4
P12 P 24
ω 2 ω 4 称为机构传动比 且等于该两构件绝对瞬心
P23
至其相对瞬心距离的反比
2
P12
ω2
1
P24
P13 返回
P34 4
ω4 P14
速度瞬心法应用例题分析二
返回
如图所示的带有一移动副的平面四杆机构中, 已知原动件2 以角速度ω2等速度转动, 现需确定机构在图示位置时从动件 4的速度v4。
？
方向：C→D ⊥CD √ √ ∥AB
A
a = 2ω v 4 k C 2C1
1 C 2C1
科氏加速度方向是将vC2C1沿牵 连角速度ω1转过90o的方向。
四、典型例题分析
如图所示为一偏心轮机构。设已知机构各构件的尺寸， 并知原动件2以角速度ω2等速度转动。现需求机构在图示位 置时，滑块5移动的速度vE、加速度aE及构件3、4、6的角速 度ω3、ω4、ω6和角加速度α3、a4、α6。
x
ω3 4 x

正确应用瞬时心法是至关重要的。我们将介绍一些使用瞬时心法的实际步骤和注意事项，以确 保准确分析和解决机械系统速度相关的问题。
瞬时心法在机械工程中的重要 性和作用
瞬时心法在机械工程中扮演着重要角色。它不仅帮助我们理解和优化机械运 动，还可以用于设计和改进各种机械系统。了解瞬时心法的重要性将使您成 为卓越的机械工程师。
机械原理第三章3-8速度 瞬心法培训课件
欢迎来到机械原理第三章培训课件！本课程将深入介绍瞬时心法的概念、原 理、应用案例和步骤，并探讨其在机械工程中的重要性和未来发展方向。
瞬时心法的概念与原理
瞬时心法是一种基于瞬时速度和运动属性的分析方法，可用于解决机械系统中的速度相关问题。它通过考虑系 统中每个点的速度和方向，帮助我们更好地理解运动轨迹和动力学特性。
瞬时心法的基本公式与计算方 法
瞬时心法的核心公式即速度瞬心公式，可以通过计算速度和位置矢量之间的 叉积来确定瞬时心的位置。同时，我们将介绍一些常用的计算方法和工具， 以便准确地应用和计算。
瞬时心法的应用案例分析
我们将通过一些实际案例来演示瞬时心法的应用。这些案例将涉及各种机械 系统，例如连杆机构、齿轮传动和曲柄机构。通过分析这些案例，我们将展 示瞬时心法在解决实际工程问题中的有效性。
瞬时心法的发展趋势与前景展 望
随着科技的进步和工程需求的变化，瞬时心法也在不断发展和演进。我们将 探讨当前的发展趋势，并展望瞬时心法在未来的应用和创新领域，为您提供 关于瞬时心法的未来前景的洞察。
总结和结论
通过学习本课程，您将全面了解瞬时心法的概念、原理和应用。我们希望本课程能够帮助您在机械工程领域取 得更大的成就，并为您的职业发展提供有力的支持。

接相
1
联
P12
纯滚动
∞ ∞
2 P12
1
绝对瞬心
P12
v12
1
2
n
2
t
1
n
t
非纯滚动
你能证明吗？
两构
P14→∞
件运
动副 直接
P23
相联
瞬
心
P12
2
位
3
4
P34
置
的
确
1
定
两构 件非 运动
N n(n 1) 4 (4 1) 6
2
2
副直 接相
P12、P23、P34、P14、P13、P24
联
1
P24
P12
P13
P34 4 P14
消元法
P12、P23、P34、P14、P13、P24
P13
3
P34
P23
4
2
1
P24
P12
P14
小结
瞬心位置求解的步骤：
1）求出瞬心数目 N n(n 1) 2
2）确定直接联接构件的瞬心位置
3）用三心定理求非直接联接构件的瞬心位置 枚举法用于构件数较少的机构，构件较多用点元法求解。
如何求？
两构
P14→∞
件运
动副 直接
P23
相联
瞬心P12Fra bibliotek2位
3
4
P34
置
的
确
1
定
两构 件非 运动
N n(n 1) 4 (4 1) 6
2
2
副直 接相
P12、P23、P34、P14、P13、P24

故相似， 所以图形 bce 称之为图形BCE的速度影像。
（2）加速度求解步骤：
★ 求aC ①列矢量方程式
aC aB aCB aB aCnB aCt B
大小：？
√ 22lBC ?
方向：∥xx
⊥AB C→B ⊥AB 加速度多边形
②确定加速度比例尺 μa((m/s2)/mm) 极点 ③作图求解未知量：
◆通过运动副直接相联两构件的瞬心位置确定
转动副联接两构件的 瞬心在转动副中心。
若为纯滚动, 接 触点即为瞬心；
移动副联接两构件 的瞬心在垂直于导 路方向的无究远处。
若既有滚动又有滑 动, 则瞬心在高副接 触点处的公法线上。
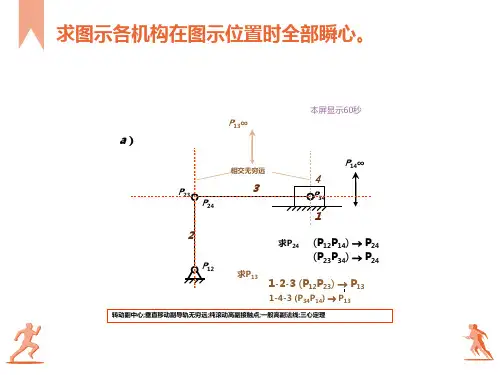
三、机构中瞬心位置的确定 （续） ◆ 不直接相联两构件的瞬心位置确定 P13
解：1. 画机构运动简图
A
2 B
ω2
D ω4 α4
ω3 a3 3 C
x
5E (E5,E6) 6 ω6 x
a6
2. 速度分析：
(1) 求vB:
（2） 求vC: 大 小
vB l AB 2
vCvBvCB
？√？
2 B
A
动件AB的运动规律和各构件 尺寸。求：
①图示位置连杆BC的角速度
和其上各点速度。
②连杆BC的角加速度和其上 C点加速度。
解题分析：原动件AB的运动规 律已知，则连杆BC上的B点速度 和加速度是已知的，于是可以用
同一构件两点间的运动关系求解。
（1） 速度解题步骤：
★求VC
①由运动合成原理列矢量方程式
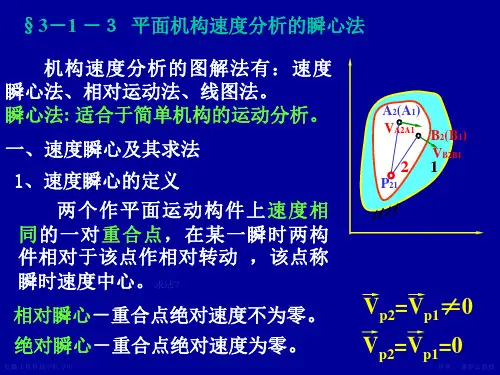
不便；速度瞬心法只限于对速度进行分析, 不能 分析机构的加速度；精度不高。
3-3 机构运动分析的矢量方程图解法
一、矢量方程图解法的基本原理和作法

在设计过程中，合理利用瞬心，可以调整机构的动态响应， 降低外部激励对机构的影响，从而减小振动和冲击。
实现机构的轻量化和紧凑化
通过优化瞬心的位置和数量，可以减小机构的整体尺寸， 实现机构的轻量化和紧凑化设计。
瞬心的合理配置有助于减少机构中的运动副数量和传动元 件，从而减小机构的重量和体积，实现轻量化和紧凑化的 目标。
随着计算机技术的发展， 越来越多的机械设计软件 提供了计算机辅助计算瞬 心的功能。
具体步骤
在软件中输入机构的参数 和运动条件，软件会自动 计算出机构的瞬心位置。
应用场景
广泛应用于各种复杂机械 系统的设计和分析中，大 大提高了设计效率。
BIG DATA EMPOWERS TO CREATE A NEW ERA
04
瞬心的计算方法
BIG DATA EMPOWERS TO CREATE A NEW
ERA
平面机构的瞬心计算方法
瞬心定义
应用场景
平面机Байду номын сангаас中，瞬时速度为零的点称为 瞬心。
在平面连杆机构、凸轮机构等中，瞬 心的计算对于确定机构的运动特性十 分重要。
瞬心计算公式
对于两构件，若它们的相对速度为零 ，则它们之间的相对瞬心位置可以通 过求解相对速度的叉乘为零的方程得 到。
详细描述
在球面机构中，如球面齿轮或球面蜗 杆，瞬心通常位于球心。通过分析瞬 心位置，可以确定机构在运动过程中 的位置和运动轨迹，有助于优化机构 的设计和运动性能。
瞬心在万向联轴器中的应用
总结词
万向联轴器中的瞬心点是连接两轴的点 ，对于实现两轴间的等角传递运动至关 重要。
VS
详细描述
在万向联轴器中，瞬心是连接两轴的点， 它确保了两轴间的等角传递运动。通过合 理选择瞬心的位置，可以优化万向联轴器 的运动性能，减小传动误差，提高传动效 率。

机械理论力学瞬心法
目录
• 瞬心法的定义与原理 • 瞬心法的计算方法 • 瞬心法在机械理论中的应用 • 瞬心法的优缺点分析 • 理
瞬心法的定义
01
02
03
瞬心法
在刚体平面运动中，通过 确定刚体上任意两点的速 度矢量，来求解刚体上任 意一点的速度矢量。
案例二：机器人关节运动中的瞬心应用
总结词
利用瞬心法分析机器人关节运动，提高机器人运动精度和稳 定性。
详细描述
在机器人关节运动中，瞬心分析有助于确定各关节的转动中 心和运动轨迹。通过瞬心法，可以精确控制机器人的姿态和 位置，提高其运动精度和稳定性。这对于实现高精度、高效 率的机器人操作具有重要意义。
THANKS
感谢观看
04
瞬心法的优缺点分析
瞬心法的优点
01
计算简便
瞬心法是一种基于几何原理的方 法，其计算过程相对简单，不需 要复杂的数学公式和计算。
直观易懂
02
03
适用范围广
瞬心法的概念直观易懂，易于理 解和掌握，对于初学者来说较为 友好。
瞬心法适用于各种类型的机构， 包括平面机构和空间机构，具有 较广的应用范围。
3
瞬心的速度可以用于进一步计算其他运动学量， 如加速度等。
计算瞬心的加速度
01 瞬心的加速度等于两个相对运动构件上速度相等 的点的加速度。
02 根据相对运动的加速度矢量关系，计算瞬心的加 速度。
03 瞬心的加速度可以用于进一步分析机械系统的动 力学特性。
03
瞬心法在机械理论中的应 用
在机构运动分析中的应用
02
瞬心法的计算方法
确定瞬心的位置
01
确定两个相对运动的构件上速度相等的点即为瞬心 的位置。

2 P23
C
3
4
D
P34
瞬心P13、P24的位置需用三心定理确又与P23、P34 在同一直
P12
12
P23
线上 故两直线P12P14 和P23P34的 P14 交点就是P24。
3
4
P34
P13
➢同理，两直线P12P14 和P23P34的交点就是P24 。
❖两构件组成纯滚动高副 接触点就是其瞬心
❖ 两构件组成滚动兼滑动高副 瞬心在接触点处两高副元素的 公法线上。
位例置：确定—图—示铰②链借四助杆三机心构定的理瞬确心定
❖三心定理：
作平面运动的三个构件的三个
瞬心位于同一直线上。
B
P12
1
A P14
❖ 瞬心P12、P23、P34、P14的位置可
直观地确定，标在图中。
瞬心的概念
瞬 心 的 概 念
瞬心 数目 位置
瞬心
瞬心就是两构件上瞬时速度相同的重合点（即 等速重合点）。
数目
位置确定—— ① 由瞬心定义确定
❖两构件组成转动副 转动副的中心就是其瞬心;
❖两构件组成移动副 其瞬心在垂直于导路 方向的无穷远处；
构件1、2之间用 P12表示
位置确定—— ① 由瞬心定义确定