机构自由度计算
- 格式:pdf
- 大小:1.47 MB
- 文档页数:28


平面机构的自由度与运动分析一、平面机构的自由度平面机构是指机构中的构件只能在一个平面内运动的机构,它由多个连接杆、转动副和滑动副组成。
平面机构的自由度是指机构中能够独立变换位置的最小的连接杆数目,也可以理解为机构中独立的变量的数量。
对于平面机构,其自由度可以通过以下公式计算:自由度=3n-2j-h其中,n表示连接杆的数量,j表示驱动链的数量,h表示外部约束的数量。
根据上述公式可以看出,自由度与平面机构中连接杆的数量和驱动链和外部约束的数量有关。
连接杆的数量越多,机构的自由度就越大,可以实现更复杂的运动。
驱动链的数量越多,机构中的动力驱动器越多,自由度就越小,机构的运动变得更加确定。
外部约束的数量越多,机构中的约束条件就越多,自由度就越小,机构的运动也会变得更加确定。
二、平面机构的运动分析1.闭合链和链架分析:首先需要确定机构中的闭合链和链架,闭合链是指机构中连接杆形成一个封闭的回路,闭合链中的连接杆数目应该为n 或n-1,n是机构中的连接杆数量。
链架是指机构中的连接杆形成一个开放的链路。
通过分析闭合链和链架中的链接关系和约束条件,可以确定机构中构件的位置和运动方式。
2.位置和速度分析:根据机构的连接杆的长度和角度,可以通过几何方法或代数方法确定机构中构件的位置和速度分量。
通过分析连接杆的长度和角度的变化规律,可以推导出机构中构件的位置和速度随时间的变化关系。
3.加速度和动力学分析:根据机构中各个构件的位置和速度,可以通过几何方法或动力学方法计算构件的加速度和动力学特性。
通过分析机构中构件的加速度和动力学特性,可以确定机构中构件的运动稳定性和质量分布。
4.动力分析:对于需要携带负载或进行力学传动的机构,需要进行动力学分析,确定机构中各个构件的受力和承载能力。
通过分析机构中构件的受力情况,可以确定机构的设计参数和强度要求。
总结起来,平面机构的自由度与运动分析是确定机构中构件位置和运动状态的重要方法,通过分析机构中的闭合链和链架、构件的位置和速度、加速度和动力学特性,可以确定机构的运动方式和特性,为机构的设计和优化提供依据。

机构自由度计算公式
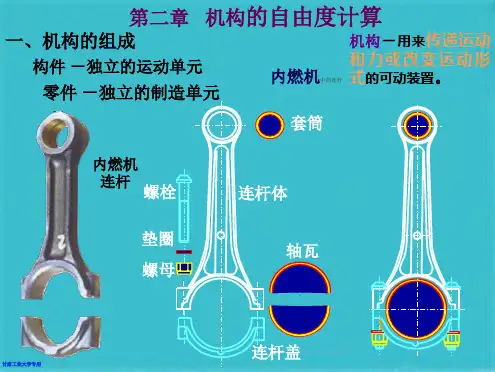
一个杆件(刚体)在平面可以由其上任一点A的坐标x和y,以及通过A点的垂线AB与横坐标轴的夹角等3个参数来决定,因此杆件具有3个自由度。
【计算公式】F=3n-(2PL +Ph ) n:活动构件数,PL:低副约束数Ph:高副约束数。
计算平面机构自由度的注意事项:
复合铰链--两个以上的构件在同一处以转动副相联。
复合铰链处理方法:如有K个构件在同一处形成复合铰链,则其转动副的数目为(k-1)个。
局部自由度:构件局部运动所产生的自由度,它仅仅局限于该构件本身,而不影响其他构件的运动。
局部自由度常发生在为减小高副磨损而将滑动摩擦变为滚动磨擦所增加的滚子处。
处理方法:在计算自由度时,从机构自由度计算公式中将局部自由度减去。
虚约束--对机构的运动实际不起作用的约束。
计算自由度时应去掉虚约束。
虚约束都是在一定的几何条件下出现的。
常见有以下几种情况:两构件联接前后,联接点的轨迹重合。
如:平行四边形机构,火车轮,椭圆仪。

机构自由度的计算公式1. 机构自由度是指一个机构、系统或者模型能够自由调整和变化的程度。
它可以用数学公式来计算,一般可以使用以下公式:机构自由度= 总体自由度- 约束自由度其中,总体自由度是指机构、系统或者模型中可以自由调整和变化的总的参数数量,而约束自由度是指受到限制和约束的参数数量。
通过计算机构自由度,我们可以了解机构的灵活性和可调整性。
2. 在机构设计中,机构自由度的计算可以进一步细分为平动自由度和转动自由度。
平动自由度是指机构中可以进行平移运动的自由度数量,转动自由度是指机构中可以进行旋转运动的自由度数量。
这两者的计算可以使用以下公式:平动自由度= 总体自由度- 转动自由度转动自由度= 总体自由度- 平动自由度通过计算平动自由度和转动自由度,我们可以更加具体地了解机构的运动方式和约束情况。
3. 在实际应用中,机构自由度的计算可以根据具体的机构结构和设计要求来确定。
通常情况下,机构自由度的计算需要考虑以下几个因素:- 约束条件:机构中的约束条件可以限制机构的运动范围和方式,需要将这些约束条件考虑进机构自由度的计算中。
- 关节数量:机构中的关节数量也会影响机构的自由度。
每个关节都可以提供一定的自由度,因此需要将关节数量考虑进机构自由度的计算中。
- 运动链路:机构中的运动链路是指连接各个部件的路径和方式。
不同的运动链路会影响机构的自由度,需要将运动链路的特性考虑进机构自由度的计算中。
综上所述,机构自由度是通过计算机构中可调整和变化的参数数量来衡量机构的灵活性和可调整性。
它可以通过总体自由度减去约束自由度来计算,也可以进一步细分为平动自由度和转动自由度。
在实际应用中,还需要考虑约束条件、关节数量和运动链路等因素来确定机构自由度的计算。

机构自由度计算方法机构自由度的计算例子机械原理机构自由度的计算是机构的结构分析的重要内容。
任何一个机构设计好以后,需要做的第一件事情就是计算机构的自由度。
机构自由度的计算公式是:F=3n—2p l—p h。
公式本身简单,只需要数出活动构件的数目n,低副的数目p l,高副的数目p h,则自由度就很容易计算了。
使用该公式有一个前提,就是要先判断出一些特殊情况:复合铰链,局部自由度和虚约束,在把这些情况都弄清楚后,再用上述公式计算,才可以得到正确的结果。
下面举一个例子,说明机构自由度的计算方法.计算图示机构的自由度,并判断该机构是否具有确定运动。
如有复合铰链、局部自由度、虚约束,请直接在题图中标出。
拿到该机构以后,第一步就是找到凸轮M,发现推杆DB尖端有一个滚子,此滚子就是局部自由度。
局部自由度几乎永远出现在滚子推杆的凸轮机构中.对于该局部自由度,处理方法是把该滚子B与BD杆焊接在一起,成为一个整体。
接着考察虚约束。
虚约束中最常见的就是某一个构件和机架之间有导路重合或者平行的移动副。
这里FH构件就在F,G,H三个地方有三个移动副与机架相联,而这三个移动副导路重合.此时只有一个起作用,其它的就是虚约束。
对于虚约束,只保留其中一个,其它的全部拿掉.最后考虑复合铰链。
复合铰链出现在转动副的地方,如果在转动副处有2个以上的构件相联,则该铰链就是复合铰链。
从上图可以看出,J点有三个构件IJ,KJ,JL相连,所以J 是复合铰链。
对于复合铰链,在计算转动副的数目时,在此处留心即可,注意这里的转动副数目等于相连的构件数目减1.综上所述,把局部自由度,虚约束,复合铰链表示出来的结果见下图这样,把滚子B和BD焊接在一起,从而去掉局部自由度;而去掉G,H这两个虚约束;J点有两个转动副。
下面进入公式的计算。
活动构件:齿轮A,齿轮M,连杆IJ,连杆KJ,连杆JL,滑块L,连杆BD(焊接了滚子B),连杆DE,连杆FH.共计9个。

机械机构自由度计算方法机械机构的自由度是指机构能够同时运动的独立方式数量。
自由度的计算是机械设计中的重要任务,它决定了机构的稳定性、可靠性和灵活性。
在机械设计中,常用的自由度计算方法有几何方法、虚功原理和单位自由度原则等。
几何方法是最常用的自由度计算方法之一,它通过分析机构的几何结构和限制条件来确定机构的自由度。
具体步骤如下:1.确定机构的构型:首先根据机械设计需求和要求,确定机构的构型和连接方式。
在确定构型时,需要考虑机构的类型和关节的数量。
2.确定机构的连接点:根据机构的构型,确定机构的连接点。
连接点是机械机构中两个或多个部件连接的位置,通过连接点可以确定机械机构的自由度。
3.统计机构的关节数目:根据机构的构型和连接点的位置,统计机构中的关节数目。
关节是机械机构中可以相对运动的部件之间的连接点。
常见的关节有转动副、滑动副、铰接副等。
4.计算机构的自由度:根据统计得到的关节数目,计算机构的自由度。
自由度的计算公式为:F=3n-m-k其中,F是机构的自由度,n是机构中的部件数目,m是机构的约束数目,k是机构中的关节数目。
约束是机械机构的运动限制条件,包括固定约束和可变约束。
虚功原理是一种基于能量守恒的自由度计算方法,它利用虚功原理来推导机械机构的自由度。
虚功原理认为,机构中的外力所做的虚功等于零。
根据虚功原理,可以设置广义坐标,通过对广义坐标的求解,可以确定机构的自由度。
单位自由度原则是一种经验法则,它根据机构的功能要求和运动方式来估计机构的自由度。
单位自由度原则认为,每个关节所提供的自由度数目大致相等。
根据单位自由度原则,可以通过统计机构中的关节数目来估计机构的自由度。
在实际机械设计中,通常会综合使用几何方法、虚功原理和单位自由度原则等来计算机构的自由度。
不同的计算方法有不同的适用范围和计算精度,需要根据具体的设计要求和情况选择合适的方法。
总之,机械机构的自由度计算是机械设计中的重要任务,它决定了机构的稳定性、可靠性和灵活性。

自由度公式
自由度计算公式:1、自由度:机构的具有确定运动所必需要的独立运动参数为机构自由度。
2、自由度计算公式:f=3n-2pl-2phn:活动构件数pl:低副数ph:高副数3、机构具有运动的条件:自由度=原动件数。
机构运动离不开自由度,自由度,分为平面机构自由度和空间机构自由度!
自由度:统计学术语:自由度(degree of freedom, df)指的是计算某一统计量时,取值不受限制的变量个数。
通常df=n-k。
其中n为样本数量,k为被限制的条件数或变量个数,或计算某一统计量时用到其它独立统计量的个数。
自由度通常用于抽样分布中。
物理学术语:自由度是指物理学当中描述一个物理状态,独立对物理状态结果产生影响的变量的数量。
如运动自由度是确定一个系统在空间中的位置所需要的最小坐标数。
例如火车车厢沿铁轨的运动,只需从某一起点站沿铁轨量出路程,就可完全确定车厢所在的位置,即其位置用一个量就可确定,我们说火车车厢的运动有一个自由度;汽车能在地面上到处运动,自由程度比火车大些,需要用两个量(例如直角坐标x,y)才能确定其位置,我们说汽车的运动有两个自由度;飞机能在空中完全自由地运动,需要用三个量(例如直角坐标x,y,z)才能确定其位置,我们说飞机在空中的运动有三个自由度。
所谓自由度数就是确定物体在空间的位置所需独立坐标的数目。
并联机构自由度计算公式并联机构是一种复杂但有趣的机械结构,而要搞清楚它的自由度,就得依靠特定的计算公式。
咱们先来说说啥是并联机构。
想象一下,你在游乐场里看到的那种刺激的过山车,它的轨道和车身之间的连接方式就有点像并联机构。
还有,工厂里那些灵活的机械臂,也是并联机构的典型应用。
并联机构的自由度啊,可不是随便就能搞明白的。
这就好比你要解开一道复杂的数学谜题,得有合适的公式和方法。
那并联机构自由度的计算公式到底是啥呢?咱们常见的并联机构自由度计算公式是:F = 6×(n - g - 1) + Σfi。
这里面的“F”代表自由度,“n”表示活动构件的数量,“g”是运动副的约束度,“fi”则是第 i 个运动副的自由度。
比如说,有一个简单的并联机构,它由三个活动构件组成,每个构件之间通过一个转动副连接,转动副的自由度是 1 ,并且有 4 个约束度。
那咱们来算算它的自由度:n = 3,g = 4,fi = 1 。
代入公式就是 F = 6×(3 - 4 - 1) + 3×1 = 3 。
这就意味着这个并联机构有 3 个自由度,它能在三维空间里进行特定的运动。
我记得有一次,在学校的实验室里,我们几个同学一起研究一个小型的并联机器人模型。
刚开始,大家都对怎么计算它的自由度一头雾水。
看着那一堆构件和连接,感觉就像走进了一个迷宫。
但是,我们没有放弃,对照着教材,一点点分析每个构件和运动副。
有个同学还因为太着急,不小心把一个零件弄掉了,找了半天才找到。
经过一番努力,终于算出了它的自由度,那一刻,大家别提多高兴了,那种成就感真是无法形容。
再来说说这个公式的应用。
在机器人领域,通过计算并联机构的自由度,可以准确地设计和控制机器人的运动,让它们能够完成各种复杂的任务,比如精准的抓取物品、进行精细的焊接操作等等。
在航空航天领域,一些卫星的姿态调整机构也采用了并联机构,通过自由度的计算,能够确保卫星在太空中稳定地运行,收集到准确的数据。
机构的自由度计算公式一、机构自由度的基本概念。
1. 定义。
- 机构的自由度是指机构具有的独立运动的数目。
它是衡量机构运动灵活性的一个重要指标。
例如,一个平面机构能够在平面内进行独立运动的方式数量就是它的自由度。
二、平面机构自由度的计算公式。
1. 一般公式。
- 对于平面机构,自由度计算公式为F = 3n - 2P_L-P_H。
- 其中,n为机构中活动构件的数目。
这里的活动构件是指能够相对运动的构件,例如在一个简单的曲柄滑块机构中,曲柄、连杆和滑块都是活动构件。
- P_L为低副的数目。
低副是指两构件之间以面接触而构成的运动副,常见的低副有转动副(如轴与轴承之间的连接,允许相对转动)和移动副(如滑块与导轨之间的连接,允许相对移动)。
- P_H为高副的数目。
高副是指两构件之间以点或线接触而构成的运动副,例如齿轮的啮合(轮齿之间为线接触)、凸轮与从动件之间的接触(点或线接触)。
2. 计算示例。
- 以曲柄滑块机构为例,它有3个活动构件(n = 3),4个低副(P_L=4,包括曲柄与机架之间的转动副、连杆与曲柄之间的转动副、连杆与滑块之间的转动副、滑块与导轨之间的移动副),没有高副(P_H = 0)。
- 根据自由度计算公式F=3n - 2P_L-P_H,可得F = 3×3-2×4 - 0=9 - 8=1,这表明曲柄滑块机构具有1个自由度,即它只有一种独立的运动方式。
3. 特殊情况说明。
- 当计算出的自由度F≤slant0时,机构一般不能运动或者是具有特殊的结构约束情况。
例如,如果F = 0,机构就成为一个刚性桁架结构,各构件之间相对位置固定,不能产生相对运动。
- 在计算自由度时,要准确判断活动构件、低副和高副的数量,有时可能存在虚约束的情况。
虚约束是一种对机构运动不起实际约束作用的约束,在计算自由度时需要去除虚约束的影响,否则会得出错误的自由度结果。
例如,在平行四边形机构中,如果存在一些对运动不起实际限制作用的约束,在计算自由度时需要正确识别并处理这些虚约束。
机构自由度的计算公式(一)机构自由度计算公式及例解什么是机构自由度?机构自由度指的是一个机构或组织在做决策时所能够自主、独立的度量。
它反映了一个机构内部成员在决策过程中的参与度,并能够量化机构内部的权力分配方式。
机构自由度计算公式机构自由度可以通过以下公式计算:机构自由度 = \frac{自主决策人数}{总决策人数} × 100\%例解1:小型企业假设某小型企业共有10位员工,其中包括2位高层管理人员和8位普通员工。
在该企业中,高层管理人员有权参与并做出最终决策,普通员工只能提供意见,但不能直接参与决策过程。
根据上述公式,可以计算该企业的机构自由度:机构自由度 = \frac{2}{10} × 100\% = 20\%这意味着该小型企业的机构自由度为20%,即只有20%的员工能够参与并影响最终的决策结果。
例解2:开放式组织考虑一个基于开放式组织原则运作的研究机构,共有50位研究人员和5位高级研究主管。
在该机构中,每位研究人员都有平等的决策权,并有权在研究项目的决策中发表意见。
使用上述公式,可以计算该研究机构的机构自由度:机构自由度 = \frac{50}{55} × 100\% ≈ \%这表示该研究机构的机构自由度约为%,即大部分的研究人员都有权参与和影响决策过程。
结论机构自由度是一个衡量机构灵活性和决策参与度的重要指标。
通过计算机构自由度可以了解一个组织内部权力的分配情况,并评估其是否具有较高的自主性和独立性。
对于不同类型的机构,机构自由度的计算方式和数值都可能有所不同,因此在实际应用中需要根据具体情况进行调整。
第二章机械零件设计概述
第一章机构自由度计算
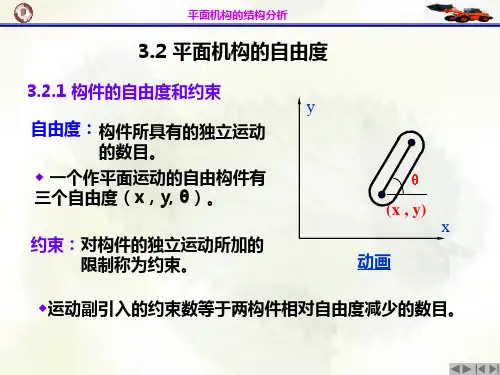
自由度与约束定义
构件独立运动的数目称为自由度
对构件运动的限制作用称为约束
对于具有n个活动构件的平面机构,若各构件之间共构成了P l 个低副和P h 个高副,则它们共引入个约束
一、平面机构的自由度计算公式
(2P l +P h )机构的自由度F 应为:
F=3×(n 个活动构件)-(2 ×低副数P l +高副数P h )=3·n -(2 P l +P h )
即=总自由度数-总约束数
的构件在同一处以转动副相联接,
这样所构成的运动副称为复合铰链
个构件在同一处形成复合铰链,则它们构成的转动副的数目为(m-1)个。
F=3*5-2*7=1
例:
1111
2
222333
34
非复合铰链情况
3
1
2
2. 局部自由度
不影响机构整体运动的自由度,称为局部自由度。
在计算机构自由度时,局部自由度应当舍弃不计。
3. 虚约束
应在计算结果中加上虚约束数,或先将产生虚约束
的构件和运动副去掉,然后再进行计算。
在机构中,有些约束所起的限制作用可能是重复的,这种不起独立限制作用的约束称为虚约束。
常见的虚约束有以下几种情况:
1)当两构件组成多个移动副,且其导路互相平行或重合时,则只有一个移动副起约束作用,其余都是虚约束。
带虚约束的凸轮机构
带虚约束的曲轴
2)当两构件构成多个转动副,且轴线互相重合时,则只有一个转动副起作用,其余转动副都是虚约束。
3)机构中对运动起重复限制作用的对称部分也往往会引入虚约束。
带虚约束的行星轮系
C
D
E
F 23
A
B
F 1
4
虚约束的本质是什么?
从运动的角度看,虚约束就是“重复的约束”或者是“多余的约束”。
机构中为什么要使用虚约束?
a.使受力状态更合理
b.使机构平衡
c.考虑机构在特殊位置的运动
使用虚约束时要注意什么问题?
保证满足虚约束存在的几何条件,在机械设计中使用虚约束时,机械制造的精度要提高。
三、平面机构具有确定运动的条件
1.F≥1或F>0
2. F=原动件数目
1
2
3
A
C B
4
D
判断图示机构能否运动?。