机构自由度的计算(1)

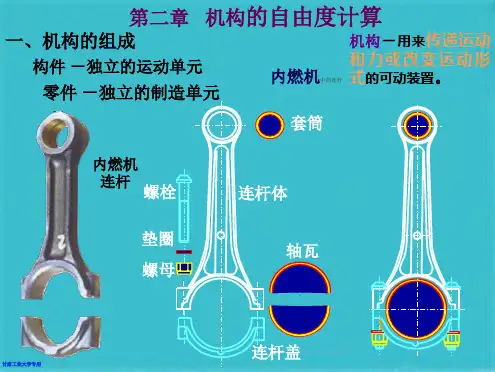
机构自由度计算公式
一个杆件（刚体）在平面可以由其上任一点A的坐标x和y，以及通过A点的垂线AB与横坐标轴的夹角等3个参数来决定，因此杆件具有3个自由度。

【计算公式】F=3n－（2PL +Ph ) n:活动构件数，PL：低副约束数Ph:高副约束数。

计算平面机构自由度的注意事项：
复合铰链－－两个以上的构件在同一处以转动副相联。

复合铰链处理方法：如有K个构件在同一处形成复合铰链，则其转动副的数目为（k-1）个。

局部自由度：构件局部运动所产生的自由度，它仅仅局限于该构件本身，而不影响其他构件的运动。

局部自由度常发生在为减小高副磨损而将滑动摩擦变为滚动磨擦所增加的滚子处。

处理方法：在计算自由度时，从机构自由度计算公式中将局部自由度减去。

虚约束－－对机构的运动实际不起作用的约束。

计算自由度时应去掉虚约束。

虚约束都是在一定的几何条件下出现的。

常见有以下几种情况：两构件联接前后，联接点的轨迹重合。

如：平行四边形机构，火车轮，椭圆仪。

机构自由度的计算公式1. 机构自由度是指一个机构、系统或者模型能够自由调整和变化的程度。

它可以用数学公式来计算，一般可以使用以下公式：机构自由度= 总体自由度- 约束自由度其中，总体自由度是指机构、系统或者模型中可以自由调整和变化的总的参数数量，而约束自由度是指受到限制和约束的参数数量。

通过计算机构自由度，我们可以了解机构的灵活性和可调整性。

2. 在机构设计中，机构自由度的计算可以进一步细分为平动自由度和转动自由度。

平动自由度是指机构中可以进行平移运动的自由度数量，转动自由度是指机构中可以进行旋转运动的自由度数量。

这两者的计算可以使用以下公式：平动自由度= 总体自由度- 转动自由度转动自由度= 总体自由度- 平动自由度通过计算平动自由度和转动自由度，我们可以更加具体地了解机构的运动方式和约束情况。

3. 在实际应用中，机构自由度的计算可以根据具体的机构结构和设计要求来确定。

通常情况下，机构自由度的计算需要考虑以下几个因素：- 约束条件：机构中的约束条件可以限制机构的运动范围和方式，需要将这些约束条件考虑进机构自由度的计算中。

- 关节数量：机构中的关节数量也会影响机构的自由度。

每个关节都可以提供一定的自由度，因此需要将关节数量考虑进机构自由度的计算中。

- 运动链路：机构中的运动链路是指连接各个部件的路径和方式。

不同的运动链路会影响机构的自由度，需要将运动链路的特性考虑进机构自由度的计算中。

综上所述，机构自由度是通过计算机构中可调整和变化的参数数量来衡量机构的灵活性和可调整性。

它可以通过总体自由度减去约束自由度来计算，也可以进一步细分为平动自由度和转动自由度。

在实际应用中，还需要考虑约束条件、关节数量和运动链路等因素来确定机构自由度的计算。

平面机构自由度的计算公式引言：平面机构是机械工程中常见的一种结构，用于实现物体在平面内的运动或变形。

在设计和分析平面机构时，了解机构的自由度是非常重要的。

本文将介绍平面机构自由度的计算公式，以帮助读者更好地理解和应用于实际工程。

一、平面机构的定义平面机构是由刚性杆件和旋转副或滑动副组成的机械系统，它们在平面内相对运动，以实现特定的功能。

平面机构通常由连接杆件、铰链和滑块等元件构成，例如四杆机构、曲柄滑块机构等。

二、自由度的概念自由度是指机构中独立运动的数量，也可以理解为机构中可以改变的参数个数。

在平面机构中，自由度是指机构中杆件和连接点的自由度，以及滑块的自由度。

自由度的数量决定了机构的运动灵活性和可控性。

三、平面机构自由度的计算公式计算平面机构自由度的公式可以根据机构的连接杆件和连接点的个数来确定。

假设平面机构有n个杆件和m个连接点，则可以使用以下公式计算自由度：自由度 = 3n - 2(m + 1)其中，3n表示每个杆件有3个自由度（平移和旋转），2(m + 1)表示每个连接点有2个约束（平移和旋转）。

通过计算，我们可以得到机构的自由度。

四、示例分析为了更好地理解平面机构自由度的计算公式，我们来看一个具体的示例。

考虑一个四杆机构，它由四个杆件和一个滑块组成。

根据公式，我们可以计算自由度：自由度 = 3(4) - 2(5 + 1) = 12 - 12 = 0从计算结果可以看出，该四杆机构没有自由度，即它是一个完全约束的机构。

这意味着杆件和滑块的位置和姿态是固定的，无法进行任何独立运动。

再考虑一个曲柄滑块机构，它由三个杆件和一个滑块组成。

根据公式，我们可以计算自由度：自由度 = 3(3) - 2(4 + 1) = 9 - 10 = -1从计算结果可以看出，该曲柄滑块机构的自由度为负数，这意味着机构存在过约束，无法实现正常运动。

这可能是由于机构设计中的错误或不合理造成的。

五、结论通过计算平面机构的自由度，我们可以对机构的运动性能和可控性进行评估和分析。

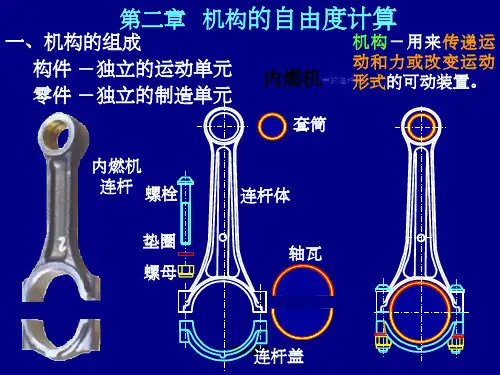
平面机构自由度的计算
平面机构自由度的计算是机械设计中的重要环节之一。

平面机构是指在同一个平面内运动的机械结构，如连杆机构、齿轮传动机构等。

自由度是指机构在运动过程中自由度的数量，即机构中自由度的个数。

平面机构自由度的计算是根据机构中约束的个数和自由度的数
量来确定的。

约束是指机构中使得某一部分运动受限制的元素，如轴承、固定点等。

自由度是指机构中可以自由运动的元素，如活动连接件、活塞等。

通常情况下，平面机构的自由度可以通过以下公式进行计算：
自由度 = 3n - m - Σfi
其中，n表示机构中的运动副数量；m表示机构中的约束数量；
Σfi表示机构中的外力或外扭矩的数量。

在实际机械设计中，平面机构自由度的计算是非常重要的，它可以帮助设计者确定机械结构的运动特性和受力情况，以保证机械结构的稳定性和可靠性。

- 1 -。

机械原理机构自由度计算要计算机械原理机构的自由度，首先需要确定机构中的连杆和连接关系。

连杆是构成机构的杆件，连接关系是将连杆连接在一起的方式。

机构中的连杆可以是刚性的或柔性的，连接关系可以通过铰链、滑动副或传动副来实现。

在计算自由度时，通常会假设连杆是刚性的，以简化计算。

计算机械原理机构的自由度时，有两种常见的方法可供选择：迭代法和非迭代法。

在迭代法中，我们首先假设机构的自由度为零，并逐步增加约束，直到无法增加为止。

每次增加约束时，我们需要检查相应的自由度是否减少。

如果自由度减少，则保留该约束；如果自由度没有减少，则将该约束排除。

通过迭代这一过程，我们最终可以得到机构的自由度。

相比之下，非迭代法更为直接。

我们可以根据机构中的约束条件和自由关系，直接计算出机构的自由度。

这种方法在约束较少或机构较简单的情况下尤其适用。

无论使用哪种方法，计算机械原理机构的自由度都需要考虑以下几个因素：1.连杆的数量：连杆的数量对机构的自由度有直接影响。

一个机构中的连杆数量越多，其自由度也就越高。

2.连杆的长度：连杆的长度决定了机构的运动幅度。

较长的连杆通常会增加机构的自由度。

3.连接关系：不同的连接关系会导致机构自由度的不同。

例如，一个通过滑动副连接的机构可能具有比通过传动副连接的机构更大的自由度。

通过对上述因素进行综合考虑，我们可以计算出机械原理机构的自由度，并据此来分析和优化机构的设计。

机构的自由度不仅与其运动性能和稳定性有关，还与动力学和控制系统的设计密切相关。

总结起来，机械原理机构的自由度计算是理解和设计复杂机构的重要步骤之一、通过迭代法或非迭代法，我们可以计算出机构的自由度，并据此分析和优化机构的性能。

在进行自由度计算时，我们需要考虑连杆的数量、长度和连接关系等因素。

这些计算为机构的设计和应用提供了理论依据。

平面机构自由度的计算公式在机械设计中，平面机构是一种由多个连杆和关节构成的机械系统，它们可以在平面内相对运动。

平面机构的自由度是指其可自由运动的独立运动参数的数量。

通过计算平面机构的自由度，可以帮助工程师理解其运动特性，并为设计和优化提供依据。

平面机构的自由度计算公式如下：f = 3n - 2j - h其中，f表示平面机构的自由度，n表示机构中连杆的数量，j表示机构中的关节数量，h表示机构中的辊子（如滚子、滑块等）数量。

这个公式的推导基于以下原理：连杆的自由度为3（平面机构中的连杆是二维的），关节的自由度为2（关节可以提供两个独立的转动或平动自由度），而辊子的自由度为1（辊子可以提供一个独立的转动或平动自由度）。

通过这个公式，我们可以得出以下结论：1. 当机构中只有连杆和关节，没有辊子时，f = 3n - 2j。

这意味着平面机构的自由度由连杆的数量和关节的数量决定。

如果机构中的连杆和关节数量满足这个公式，那么机构就是可移动的；否则，机构将被限制在某些特定的位置。

2. 当机构中有辊子时，f = 3n - 2j - h。

这意味着辊子的存在会进一步减少平面机构的自由度。

辊子的数量越多，机构的自由度就越少。

3. 当机构的自由度为零时，说明机构是固定的，无法进行任何运动。

通过这个公式，我们可以对平面机构的自由度进行快速计算和分析。

在设计过程中，我们可以根据自由度的要求来选择合适的机构类型和参数，以满足设计需求。

例如，如果我们需要设计一个可以在平面内进行旋转和平移的机构，我们可以使用公式来计算自由度，并根据结果选择合适的连杆数量和关节数量。

如果结果符合要求，我们可以进一步优化机构参数以满足其他设计要求。

总结：平面机构的自由度计算公式为 f = 3n - 2j - h，其中n表示机构中连杆的数量，j表示机构中的关节数量，h表示机构中的辊子数量。

这个公式可以帮助工程师快速计算和分析平面机构的自由度，为机构的设计和优化提供依据。