第4章网络的状态方程

格式：ppt
大小：1.86 MB
文档页数：33

下载文档原格式

第4章网络的状态方程

预解
矩阵
频域解
X ( s ) s 1 A 1 X ( 0 ) s 1 A 1 B F ( s ) ( s ) s 1 A 1
时域解
零输入零状态
X(t)(t)X(0)0 t(t)Bf()d
(t)L1(s)
状态转移矩阵
固有特性
31
X(t)(tt0)X(t0)
t(t)Bf
Bf
Q Q11TT21
Q2T1 Q2T2
Q3T1 Q3T2
Q4T1 Q4T2
1Il 0
0 1Ll
0 0
0 0
Q Q11T T43
Q2T3 Q2T4
Q3T3 0
0 0
0
0 1Rl
0
0 0 0 1Cl
B43B440 Ql BtT Q34B4T30
5
描述变量
支路电流和电压向量分别表示为
i b i t 1i t 2i t 3i t 4i l 1i l 2i l 3i l 4 T
第4章网络的状态方程
第4章网络的状态方程
暂态电路的分析方法
传统分析法（用高阶微分方程描述电路）状态变量分析法
状态变量分析法特点
①易于编制计算机求解程序； ②它是非线性、时变网络最常用的分析方法； ③是对网络作定性分析的最有力的工具之一。
主要内容
状态方程的建立状态方程的求解
系统编写法多端口法
0 .1 6 6 6 7
0
.0
4
7
6
2
V s
0 . 4 0 9 5 3
29
4.5 网络状态方程的解
状态方程适宜于采用数值求解
dVt2
dVt1

数字电子技术基础第四章习题及参考答案

数字电子技术基础第四章习题及参考答案第四章习题1．分析图4-1中所示的同步时序逻辑电路，要求：（1）写出驱动方程、输出方程、状态方程；（2）画出状态转换图，并说出电路功能。

CPY图4-12．由D触发器组成的时序逻辑电路如图4-2所示，在图中所示的CP脉冲及D作用下，画出Q0、Q1的波形。

设触发器的初始状态为Q0=0，Q1=0。

D图4-23．试分析图4-3所示同步时序逻辑电路，要求：写出驱动方程、状态方程，列出状态真值表，画出状态图。

CP图4-34．一同步时序逻辑电路如图4-4所示，设各触发器的起始状态均为0态。

（1）作出电路的状态转换表；（2）画出电路的状态图；（3）画出CP作用下Q0、Q1、Q2的波形图；（4）说明电路的逻辑功能。

图4-45．试画出如图4-5所示电路在CP波形作用下的输出波形Q1及Q0，并说明它的功能（假设初态Q0Q1=00）。

CPQ1Q0CP图4-56．分析如图4-6所示同步时序逻辑电路的功能，写出分析过程。

Y图4-67．分析图4-7所示电路的逻辑功能。

（1）写出驱动方程、状态方程；（2）作出状态转移表、状态转移图；（3）指出电路的逻辑功能，并说明能否自启动；（4）画出在时钟作用下的各触发器输出波形。

CP图4-78．时序逻辑电路分析。

电路如图4-8所示：（1）列出方程式、状态表；（2）画出状态图、时序图。

并说明电路的功能。

1C图4-89．试分析图4-9下面时序逻辑电路：（1）写出该电路的驱动方程，状态方程和输出方程；（2）画出Q1Q0的状态转换图；（3）根据状态图分析其功能；1B图4-910.分析如图4-10所示同步时序逻辑电路，具体要求：写出它的激励方程组、状态方程组和输出方程，画出状态图并描述功能。

1Z图4-1011．已知某同步时序逻辑电路如图4-11所示，试：（1）分析电路的状态转移图，并要求给出详细分析过程。

（2）电路逻辑功能是什么，能否自启动？（3）若计数脉冲f CP频率等于700Hz，从Q2端输出时的脉冲频率是多少?CP图4-1112．分析图4-12所示同步时序逻辑电路，写出它的激励方程组、状态方程组，并画出状态转换图。

状态方程是描述状态参数之间关系的方程

一、概述状态方程是描述状态参数之间关系的数学原理，它在控制系统、热力学、化学动力学等领域都有广泛的应用。

状态参数可以是物理系统的变量，也可以是系统的特定特征。

通过建立状态方程，我们可以更好地理解和控制系统的行为，从而实现系统的优化和改进。

本文将从状态方程的定义、应用和实际意义等方面展开讨论。

二、状态方程的定义状态方程是描述系统状态参数之间关系的数学方程。

在控制系统中，状态参数可以是系统的位置、速度、加速度等动态变量，也可以是系统的输入、输出变量。

状态方程通常用微分方程的形式表示，如dx/dt = Ax + Bu，其中 x 是系统的状态向量，A 是状态矩阵，B 是输入矩阵，u 是系统的输入向量。

通过状态方程，我们可以描述系统状态的演化和系统输入对状态的影响，从而实现对系统行为的预测和控制。

三、状态方程的应用1. 控制系统中的应用在控制系统中，状态方程被广泛应用于系统建模和控制器设计。

通过状态空间法建立系统的状态方程，我们可以方便地分析系统的稳定性、可控性和可观性等性质，从而设计出满足系统性能要求的控制器。

状态方程还可以用于系统的状态估计和滤波，提高系统的鲁棒性和稳定性。

2. 热力学中的应用在热力学领域，状态方程通常用于描述热力学系统的状态变化和能量转化过程。

通过建立热力学系统的状态方程，我们可以实现对系统的热力学特性进行定量分析和优化设计。

通过状态方程可以描述理想气体的状态方程，从而研究气体的热力学性质和行为。

3. 化学动力学中的应用在化学动力学中，状态方程被用于描述化学反应系统的状态变化和反应动力学性质。

通过建立化学反应系统的状态方程，我们可以分析反应速率、平衡常数等重要参数，从而优化反应条件和提高反应效率。

四、状态方程的意义和作用1. 了解系统的动态行为通过状态方程，我们可以了解系统的动态行为和状态演化规律。

系统的状态方程可以描述系统的状态变化和受控制因素对状态的影响，从而帮助我们更好地理解系统的行为。

状态空间表达式

（28）状态空间方程实现非唯一，书p28, 图1.16b求得其对应的传递函数为：（29）
为求得令式（29）与式（26）相等，通过对多项式系数的比较得：故得：（30）
也可将式(30)写成式(31)的形式，以便记忆。（31）
将上图a的每个积分器输出选作状念变最，如图所示，得这种结构下的状态空间表达式：
解：
→
→
u
y
－
＋
例：解：比例积分环节： → → u y ＋
例：
解：
综合惯性环节、积分环节模拟结构图得：
u
y
－
＋
u
y
解：选积分器的输出为状态变量得：
u
y
状态方程：
输出方程：
状态空间表达式
1.3.2 从系统的机理出发建立状态空间表达式
一般常见的控制系统，按其能量属性，可分为电气、机械、机电、气动液压、热力等系统。根据其物理规律，如基尔霍夫定律、牛顿定律、能量守恒定律等，即可建立系统的状态方程。当指定系统的输出时，很容易写出系统的输出方程。
同一系统，经非奇异变换后，得：
其特征方程为：
（44）
1.5.2 系统特征值的不变性及系统的不变量
1.系统特征值
式(43)与式(44)形式虽然不同，但实际是相等的，即系统的非奇异变换，其特征值是不变的。可以证明如下：
将特征方程写成多项式形式由于特征值全由特征多项式的系数唯一确定，而特征值经非奇异变换是不变的，那么这些系统也是不变的量。所以称特征多项式的系数为系统的不变量。
(3)有共轭复根时，以四阶系统其中有一对共轭复根为例，即此时
1.6 从状态空间表达式求传递函数阵
1.6.1 传递函数(阵)

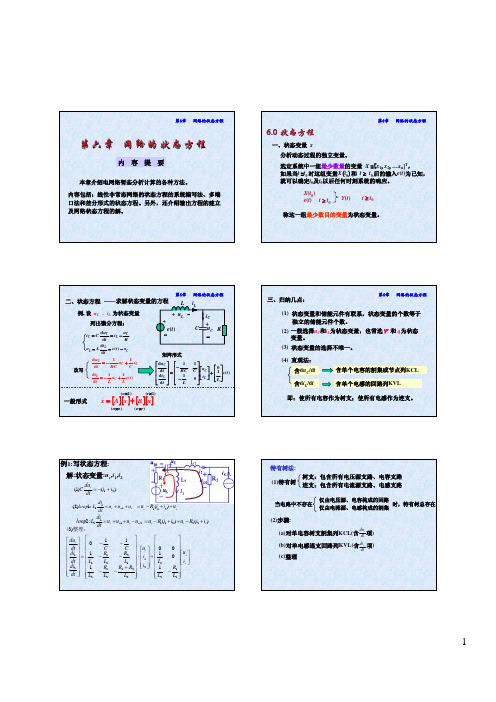
网络的状态方程

二、状态方程 ——求解状态变量的方程 L iL
例.设 uC , iL 为状态变量列出微分方程：
iC
=C
duC dt
=
iL
−
uC R
+ uL -
+
-e(t)
C
iC + uC R -
uL
=
L diL dt
=
e(t ) − uC
改写
duC dt
=−
1 RC
uC
+1 C
iL
diL dt
=
−
1 L uC
+
1 e(t) L
C
duC dt
+iL1 +iL2
=
us
− uC R1
(3)
duC dt
=
1 C
(−iL1
−
iL2
− uC ) + us R1 CR1
令L1L2-M2=Δ
整理得状态方程的矩阵形式为
diL1 dt
=
1 L1L2 −
M2
[0 −
MR2iL2
+ (M
+
L2)uC ]+
1 L1L2 − M 2
(MR2is
− Mus )
duc dt
项)
(b)对单电感连支回路列KVL(含diL 项)
dt
(c)整理
1
例2.写状态方程
解：KCL
:
⎪⎧C2
⎪
⎨ ⎪
C3
du2
dt du3
dt
= i7 = i7
−
i6
⎪⎩C4
du 4 dt
=

第4章稳定性与李雅普诺夫方法

21
4.3 李雅普诺夫第二法
3、希尔维斯特判据
设实对称阵
p11 p12
P
p21
p22
pn1
p1n
,
pij
p ji
pnn
i 为其各阶顺序主子式，即
1 p11 ,
2
p11 p21
p12 , p22
,n P
矩阵P或V(x)定号性的充要条件是：
22
4.3 李雅普诺夫第二法
(1)若 i 0 (i 1, 2, , n)，则 P 正定；
要条件是整个状态空间只有一个平衡点。
线性系统：渐近稳定大范围渐近稳定非线性系统：一般小范围渐近稳定
6
4. 不稳定
4.1.2 稳定性的几个定义
对于某个实数和任意
，在超球域
内始终存在状态，使得从该状态开始的运动轨迹要突破超球域。
7
4.1.2 稳定性的几个定义
此三个图分别表示平衡状态为稳定、渐近稳定和不稳定时初始扰动所引起的典型轨迹。
28
4.3 李雅普诺夫第二法
说明：（1）V (x) 0 ，则此时 V (x) C，系统轨迹将在某个曲面上，
而不能收敛于原点，因此不是渐近稳定。（2）V (x)不恒等于0，说明轨迹在某个时刻与曲面 V (x) 相C 交，
但仍会收敛于原点，所以是渐近稳定。
x0
x0
（3）稳定判据只是充分条件而非必要条件！
于是知系统在原点处不稳定。
33
4.3 李雅普诺夫第二法
4.3.3 对李雅谱诺夫函数的讨论（1） V(x)是正定的标量函数，V(x)具有一阶连续偏导数；（2）并不是对所有的系统都能找到V(x)来证明该系统稳定或者不稳定；（3）V(x)如果能找到，一般是不唯一的，但关于稳定性的结论是一致的；

第四章状态空间模型

t)
=
f(
X(t),u
(t),
t)
状态方程
Y(t) =g(X(t), u(t),t) 输出方程
三、差分方程与离散变量的状态空间表达式
三、差分方程与离散变量的状态空间表达式
三、差分方程与离散变量的状态空间表达式
离散系统方程
离散系统系统方程 X(k+1) = F X(k)+ GU(k) 状态方程 Y(k) = CX(k) + DU(k) 输出方程 ห้องสมุดไป่ตู้统的阶数
七、状态方程应用之二——人口模型
七、状态方程应用之二——人口模型
七、状态方程应用之二——人口模型
七、状态方程应用之二——人口模型
七、状态方程应用之二——人口模型
(4)利用模型可研究以下问题： 1）死亡率变化的影响 2）人口扰动的影响 3）计划生育的影响
八、状态方程应用之三——预测产品销售量
第四章状态空间模型（数学模型）
（数学）模型建模概论
机理法建模（人口预测模型）拟合法建模两类系统及其相应状态空间系统方程离散系统连续系统
状态空间方程实例
连续系统：宏观经济模型离散系统：1 人才系统；2 宏观经济模型； 3 人口迁移模型
第一节数学模型建模方法概述
1数学模型定义
第二节状态空间系统方程
两类系统
连续系统：工程系统。（微分方程描述）离散系统：如银行存款本利和（差分方程描
述）。社会经济系统大多为离散系统。
例 1 宏观经济系统模型例2 银行储蓄
m
图3-13 一般机
例3-4
例3-4
例3-5
例3-5
例3-5
连续系统方程

电路-状态方程

第7章一阶电路和二阶电路的时域分析状态方程的概念会写电路的状态方程状态方程√ 状态方程的列写 √ 输出方程的列写 √状态变量的选择状态方程的求解（时域或频域求解） × 输出方程的求解（时域或频域求解） ×2010/11/1电路自动化科学与电气工程学院11、状态和状态变量状态电路在tk时刻的状态是指在该时刻电路所必须具有的一组独立完备数据，这组数据不仅反映了tk 时刻以前所有输入对电路的作用效果，而且结合（tk，t）期间的输入就能够完全确定t时刻电路的特性。

2010/11/1电路自动化科学与电气工程学院2状态变量一组独立的网络变量(1)这组变量在t=t0时刻的值和从t=t0开始的输入能唯一决定这组变量在任何时刻t>t0时的值。

(2) t时刻的这组变量值和t时刻的输入值能唯一决定网络的任一变量在时刻t的值。

则这组变量称为状态变量,由这组变量构成的集合称为网络的状态。

通常选独立的电容电压和电感电流作为网络的状态变量2010/11/1 电路自动化科学与电气工程学院 32. 状态方程和输出方程tRLiLuCd uC C = iL dtuSuRuLCd uC 1 = iL d 2 uC d uC + RC + uC = uS LC dt C 2 dt dt d iL 1 R 1 = − u C − iL + u S dt L L Ld iL uS = RiL + L + uC dtt >0⎡ d uC ⎤ ⎡ ⎢ dt ⎥ ⎢ 0 ⎢ ⎥=⎢ ⎢ d iL ⎥ ⎢ − 1 ⎢ dt ⎥ ⎢ L ⎣ ⎦ ⎣2010/11/11 ⎤ ⎡0⎤ C ⎥ ⎡ uC ⎤ ⎢ ⎥ ⎥ ⎢ ⎥ + 1 [uS ] R ⎥ ⎣ iL ⎦ ⎢ ⎥ − ⎣L⎦ ⎥ L⎦电路自动化科学与电气工程学院4⎡ x1 ⎤ ⎡ x1 ⎤ ⎢ x ⎥ = A ⎢ x ⎥ + B [ uS ] ⎣ 2⎦ ⎣ 2⎦状态方程的标准形式：χ=A χ+B ν状态方程是状态向量的一阶微分方程，描述了电路中有记忆元件的输入－输出关系，体现了电路的动态特性。

05、第4章-线性动态方程和脉冲响应矩阵

第四章线性动态方程和脉冲响应矩阵4.1 引言4.2 动态方程的解4.3 等价动态方程4.4 脉冲响应矩阵和动态方程从数学的角度讲，就是相对于给定的初始x0和外输入作用u，求解状态方程的解，即由初始状态和外输入作用所引起的响应。

一个主要问题。

x=A(t)x+B(t)u(t)y(t)=C(t)x+E(t)u(t)的解的性质。

定理：（解的存在和唯一性）设A及f的每个元素a ij (t )，f i 均在上连续，则对于任何及任何常向量x 0，方程恒有定义在整个上的解x=x(t )，满足初值条件：(,)−∞+∞0(,)∈−∞+∞t (,)−∞+∞00()=x x t 并且方程也只能有一个解满足。

N N 1111211221()()()()()()⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ " %#%## "" n n n nn n t x a t a t a t x x x x a t a t x x xA 说明：=A(t )x 打开后的形式是： x 因此，其解向量x(t ) 必然属于。

称是微分方程的一个解，系指：\n()t Ψ()()()= A t t t ΨΨ定理4－1：方程d x/dt=A(t)x 的所有解的集合，形成在实数域上的n 维向量空间。

定理4－1包含以下两层意义：a)解的集合组成线性空间；b)解空间的维数是n。

分成两部分证明：1）dx/dt=A(t)x有n个线性无关的解；2）其任一解均可表成它们的线性组合。

0()e i i t =Ψ(i =1，2，…，n )()xA x = t 时方程的解。

要证明，是线性无关的n 个解。

12,,,n "ΨΨΨ()i t Ψ始条件是n 个线性无关的向量，是在初12,,,e e e n "1)设b)证明解空间的维数是n ：12[]0=∀"n t ΨΨΨα反证法：若线性相关，必存在一个n ×1非零实向量α使得12,,,n"ΨΨΨ特别，当t =t 0时就有1200012[()()()][]0e ee nn t t t ==""ΨΨΨαα12,,,e e e n "上式意味着向量组线性相关，这与初始假设矛盾。

《数字电子技术基础》课后习题答案

《数字电子技术基础》课后习题答案《数字电路与逻辑设计》作业教材：《数字电子技术基础》（高等教育出版社，第2版，2012年第7次印刷）第一章：自测题：一、1、小规模集成电路，中规模集成电路，大规模集成电路，超大规模集成电路5、各位权系数之和，1799、01100101，01100101，01100110；11100101，10011010，10011011二、1、×8、√10、×三、1、A4、B练习题：1.3、解：(1) 十六进制转二进制： 4 5 C0100 0101 1100二进制转八进制：010 001 011 1002 13 4十六进制转十进制：(45C)16=4*162+5*161+12*160=(1116)10所以：(45C)16=(10001011100)2=(2134)8=(1116)10(2) 十六进制转二进制： 6 D E . C 80110 1101 1110 . 1100 1000二进制转八进制：011 011 011 110 . 110 010 0003 3 3 6 . 6 2十六进制转十进制：(6DE.C8)16=6*162+13*161+14*160+13*16-1+8*16-2=(1 758.78125)10所以：(6DE.C8)16=(011011011110. 11001000)2=(3336.62)8=(1758.78125)10(3) 十六进制转二进制：8 F E . F D1000 1111 1110. 1111 1101二进制转八进制：100 011 111 110 . 111111 0104 3 7 6 . 7 7 2十六进制转十进制：(8FE.FD)16=8*162+15*161+14*160+15*16-1+13*1 6-2=(2302.98828125)10所以：(8FE.FD)16=(100011111110.11111101)2=(4376.772)8=(2302.98828125)10(4) 十六进制转二进制：7 9 E . F D0111 1001 1110 . 1111 1101二进制转八进制：011 110 011 110 . 111 111 0103 6 3 6 . 7 7 2十六进制转十进制：(79E.FD)16=7*162+9*161+14*160+15*16-1+13*16 -2=(1950. 98828125)10所以：(8FE.FD)16=(011110011110.11111101)2=(3636.772)8=(1 950.98828125)101.5、解：(74)10 =(0111 0100)8421BCD=(1010 0111)余3BCD (45.36)10=(0100 0101.0011 0110)8421BCD=(0111 1000.0110 1001 )余3BCD(136.45)10=(0001 0011 0110.0100 0101)8421BCD=(0100 0110 1001.0111 1000 )余3BCD (374.51)10=(0011 0111 0100.0101 0001)8421BCD=(0110 1010 0111.1000 0100)余3BCD1.8、解（1）(+35)=(0 100011)原= (0 100011)补（2）(+56 )=(0 111000)原= (0 111000)补（3）(-26)=(1 11010)原= (1 11101)补（4）(-67)=(1 1000011)原= (1 1000110)补第二章：自测题：一、1、与运算、或运算、非运算3、代入规则、反演规则、对偶规则二、2、×4、×三、1、B3、D5、C练习题：2.2：（4）解：Y=AB̅+BD+DCE+A̅D=AB̅+BD+AD+A̅D+DCE=AB̅+BD+D+DCE=AB̅+D (B +1+CE ) =AB̅+D （8）解：Y =(A ̅+B ̅+C ̅)(D ̅+E ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅(A ̅+B ̅+C ̅+DE ) =[(A ̅+B ̅+C ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅+(D ̅+E ̅)̅̅̅̅̅̅̅̅̅̅](A ̅+B ̅+C ̅+DE ) =(ABC +DE )(ABC ̅̅̅̅̅̅+DE ) =DE 2.3：（2）证明：左边=A +A ̅(B +C)̅̅̅̅̅̅̅̅̅̅̅̅ =A +A ̅+(B +C)̅̅̅̅̅̅̅̅̅̅=A +B̅C ̅ =右式所以等式成立（4）证明：左边= (A̅B +AB ̅)⨁C = (A̅B +AB ̅)C ̅+ (A ̅B +AB ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅C = (A ̅BC ̅+AB ̅C ̅)+A ̅B ̅̅̅̅⋅AB̅̅̅̅̅⋅C =A̅BC ̅+AB ̅C ̅+(A +B ̅)(A ̅+B )C =A̅BC ̅+AB ̅C ̅+(AB +A ̅B ̅)C =A̅BC ̅+AB ̅C ̅+ABC +A ̅B ̅C 右边= ABC +(A +B +C )AB ̅̅̅̅⋅BC ̅̅̅̅⋅CA̅̅̅̅ =ABC +(A +B +C )[(A̅+B ̅)(B ̅+C ̅)(C ̅+A ̅)] =ABC +(A +B +C )(A̅B ̅+A ̅C ̅+B ̅+B ̅C ̅)(C ̅+A ̅)=ABC +(A +B +C )(A̅B ̅C ̅+A ̅C ̅+B ̅C ̅+A ̅B ̅) =ABC +AB̅C ̅+A ̅BC ̅+A ̅B ̅C 左边=右边，所以等式成立 2.4（1）Y ′=(A +B ̅C ̅)(A ̅+BC) 2.5（3）Y ̅=A ̅B ̅(C ̅+D ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ C ̅D ̅(A ̅+B ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ 2.6：（1）Y =AB +AC +BC=AB (C +C̅)+AC (B +B ̅)+BC (A +A ̅) =ABC +ABC ̅+AB ̅C +A ̅BC 2.7：（1）Y =A ̅B ̅+B ̅C ̅+AC +B ̅C 卡诺图如下： B C A 00 0111100 1 1 1111所以，Y=B̅+AC2.8：（2）画卡诺图如下：B C A 0001 11 100 1 1 0 11 1 1 1 1Y(A,B,C)=A+B̅+C̅2.9：（1）画Y(A,B,C,D)=∑m(0,1,2,3,4,6,8)+∑d(10,11,12,13,14)如下：CDAB00 01 11 1000 1 1 1 101 1 111 ×××10 1 ××Y (A,B,C,D )=A̅B ̅+D ̅ 2.10：（3）解：化简最小项式： Y =AB +(A̅B +C ̅)(A ̅B ̅+C ) =AB +(A̅B A ̅B ̅+A ̅BC +A ̅B ̅C ̅+C ̅C ) =AB (C +C̅)+A ̅BC +A ̅B ̅C ̅ =ABC +ABC ̅+A ̅BC +A ̅B ̅C ̅ =∑m (0,3,6,7)最大项式：Y =∏M(1,2,4,5) 2.13：（3）Y =AB̅+BC ̅+AB ̅C ̅+ABC ̅D ̅ =AB̅(1+C ̅)+BC ̅(1+AD ̅) =AB̅+BC ̅ =AB̅+BC ̅̿̿̿̿̿̿̿̿̿̿̿̿ = AB̅̅̅̅̅∙BC ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅技能题：2.16 解：设三种不同火灾探测器分别为A 、B 、C ，有信号时值为1，无信号时为0，根据题意，画卡诺图如下：B C A 00 01 11 10 0 0 0 1 0 1 0 1 1 1Y =AB +AC +BC=AB +AC +BC ̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿=AB ̅̅̅̅⋅AC ̅̅̅̅⋅BC ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=(A ̅+B ̅)(A ̅+C ̅)(B ̅+C ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅+B ̅̅̅̅̅̅̅̅̅+A ̅+C ̅̅̅̅̅̅̅̅̅+B ̅+C ̅̅̅̅̅̅̅̅̅第三章：自测题：一、1、饱和，截止7、接高电平，和有用输入端并接，悬空；二、1、√8、√；三、1、A4、D练习题：3.2、解：(a)因为接地电阻4.7k Ω，开门电阻3k Ω，R>R on ，相当于接入高电平1，所以Y =A ̅B ̅1̅̅̅̅̅̅=A +B +0=A +B(e) 因为接地电阻510Ω，关门电0.8k Ω，R<R off ，相当于接入高电平0，所以、Y =A +B +0̅̅̅̅̅̅̅̅̅̅̅̅̅=A̅⋅B ̅∙1̅̅̅̅̅̅̅̅̅̅=A +B +0=A +B3.4、解：(a) Y1=A+B+0̅̅̅̅̅̅̅̅̅̅̅̅̅=A+B̅̅̅̅̅̅̅̅(c) Y3=A+B+1̅̅̅̅̅̅̅̅̅̅̅̅̅=1̅=0(f) Y6=A⋅0+B⋅1̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=B̅3.7、解：(a) Y1=A⨁B⋅C=(A̅B+AB̅)C=A̅BC+AB̅C3.8、解：输出高电平时，带负载的个数2020400===IHOHOH I I NG 可带20个同类反相器输出低电平时，带负载的个数78.1745.08===ILOLOL I I NG 反相器可带17个同类反相器3.12EN=1时，Y 1=A ， Y 2=B ̅EN=0时，Y 1=A ̅， Y 2=B3.17根据题意，设A为具有否决权的股东，其余两位股东为B、C，画卡诺图如下，BCA00 01 11 100 0 0 0 01 0 1 1 1则表达结果Y的表达式为：Y=AB+AC=AB+AC̿̿̿̿̿̿̿̿̿̿̿̿=AB̅̅̅̅⋅AC̅̅̅̅̅̅̅̅̅̅̅̅̅̅逻辑电路如下：技能题：3.20：解：根据题意，A、B、C、D变量的卡诺图如下：CD AB00 01 11 1000 0 0 0 001 0 0 0 011 0 1 1 110 0 0 0 0Y =ABC +ABD =ABC +ABD ̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿=ABC ̅̅̅̅̅̅⋅ABD ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅电路图如下：第四章：自测题：一、2、输入信号，优先级别最高的输入信号7、用以比较两组二进制数的大小或相等的电路，A>B 二、3、√4、√三、5、A7、C练习题：4.1；解：(a) Y =A⨁B +B ̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅B +AB ̅+B ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅B +B ̅̅̅̅̅̅̅̅̅̅̅=A ̅+B̅̅̅̅̅̅̅̅̅=AB ，所以电路为与门。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

端口：端口：L
电流源 C
电压源
多端口电阻网络可含受控源）（可含受控源）
12
多端口描述方程
VL V1 = Vis H12 H 22 H12 a H12 c H 22 a H 22 c i1 V 2 iL i1 = is VS V2 = VC ivs i2 = iC
10
dV C 1 dt −G1 0 C1 + C2 0 0 dV C 3 = 0 C3 0 dt 0 0 L1 + L2 d i −1 L2 dt dV S dt C2 0 0 0 0 0 di S 1 + dt 0 L1 0 di S1 dt
16
解：参见例4－4
−4 13 H11 = −4 12.314
−0.1667 −0.1667 H12 = −0.3619 −0.0952 0.1667 0.3619 H 21 = 0.1667 0.0952 0.070635 0.003968 H 22 = 0.003968 0.059523
H 21a = [ 0.1667 0.3619]
H 21c = [ 0.1667 0.0952]
18
H 22 a = 0.070635
1 0 L−1 = 0 0.5
H 22b = 0.003968
H 22 c = 0.003968
H 22 d = 0.059523
C −1 = [1]
3
描述矩阵
Q f = [1t
Ql ]
Il Q11 Q21 Q31 Q41
Lt
B f = [ Bt
1l ]
V t Ct
Rt
Lt
Ll Q12 Q22 Q32 Q42
Il
Rl Cl Q13 Q14 Q23 Q24 Q33 Q34 Q43 Q44
Ll Q43 = Q44 = 0
Qf =
0 −G4 0
1 VC1 0 0 0 VS 0 V C 3 + 0 1 −1 i S 1 − R2 i L 2 1 0 0 i S 1
11
4.2 多端口法
含受控源的线性、非线性（电容、电感）含受控源的线性、非线性（电容、电感）常态网络
iL i1 = is VS V2 = VC
dVC iC = −C dt
选第1、4行，整理得
14
di L dt H −1 11a =M d VC H 21c dt
H12b i L H11b −1 V + M H H 22 d C 21d
0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1
0 0 0 1
1
0
1 0 1 0
0 0 0 1 0 0 0 0
0 −1 1 0 0 0
0 1 0 0 0 −1 1
0 −1 0 0
1 −1 0 0 0 0
Q14 Q13
9
Q33T
17
H11a H 11c H 21a H 21c
H11b H11d H 21b H 21d
H12 a H12 c H 22 a H 22 c
H12b H12 d H 22b H 22 d
−4 13 H11 = −4 12.314 −0.1667 −0.1667 H12 = −0.3619 −0.0952 0.1667 0.3619 H 21 = 0.1667 0.0952
H11a H 11c = H 21a ivs i2 = H 21c iC
端口描述方程 diL VL = − L dt
H11b H11d H 21b H 21d
H12 a H12 c H 22 a H 22 c
H12b H12 d H 22b H 22 d
−4 13 H11a = H11 = −4 12.314
H12 a
−0.1667 = −0.3619
H12b
−0.1667 = −0.0952
0.070635 0.003968 H 22 = 0.003968 0.059523
H12 a i s H 22 c V s
− L 0 M = 0 −C
修正后可用于非常态网络
15
例4-2 图4-3 所示电路 R1 = R3 = R6 = 6Ω
，R2 = 5Ω，
， R4 = R8 = 12Ω ，R5 = 20Ω ， R7 = 16Ω ， R9 = 14Ω ，L1 = 1H ， L2 = 2H ，C = 1F 现以 iL1 、 iL 2 、VC 为状态变量试建立状态方程。状态变量试建立状态方程。
iC k
where
≈
GCVC k
+is ( k −1)
C GC = ∆t
is ( k −1) = −GCVC ( k −1)
21
等效电路
iC k
≈
直流电阻网络
GCVC k
+is ( k −1)
iLk
≈ GLVLk
计算电路线性）（线性）
+is ( k −1)
22
电压源
利用节点电压法
电流源
Vnk = Yn −1 − Ais ( k −1) + AYbVs − Ais
T
Vb = [Vt1 Vt 2 Vt 3 Vt 4 Vl1 Vl 2 Vl 3 Vl 4 ]
描述方程
T
Q f ib = 0 n − 1
B f Vb = 0
b − n +1
电阻
V t 3 = R ti
t3
i l 3= G lV l 3
V t 4 L t t V = L l2 lt
T −Q41 1I l 0 0 T −Q42 0 1L l 0 0 0 0 1R l
0
0
0
0
0
T B43 = B44 = 0 Ql = − Bt
T Q34 = − B43 = 0
描述变量支路Leabharlann 流和电压向量分别表示为状态变量
ib = [it1 it 2
it 3
it 4
il1 il 2
il 3
il 4 ]
0 0 1V t 0 0 1 0 0 Ct 0 1R t 0 0 0 0 1L t 0
Vt Ct
T −Q21 T −Q22 T −Q23 T −Q24
？
1C l 0 0 0
4
Rt
T −Q31 T −Q32 T −Q33
Rl Cl
T −Q11 T B f = −Q12 T −Q13 T −Q14
iL (tk ) ≈ GLVL (tk ) +is (tk −1 ) iLk
where
≈ GLVLk
+is ( k −1)
∆t GL = L
is ( k −1) = iL (tk −1 )
20
电容
VC (tk ) − VC (tk −1 ) iC (tk ) ≈ C ∆t
iC (tk ) ≈ GCVC (tk ) +is (tk −1 )
0 −1 0 M −1 = 0 −0.5 0 0 0 1
diL1 dt diL 2 = dt dV C dt
4 0.1667 −13 2 −6.1572 0.0476 −0.1667 −0.0952 −0.0595
第4章网络的状态方程
暂态电路的分析方法传统分析法（用高阶微分方程描述电路）传统分析法（用高阶微分方程描述电路）状态变量分析法
状态变量分析法特点
①易于编制计算机求解程序；易于编制计算机求解程序； ②它是非线性、时变网络最常用的分析方法；它是非线性、时变网络最常用的分析方法； ③是对网络作定性分析的最有力的工具之一。是对网络作定性分析的最有力的工具之一。系统编写法状态方程的建立
主要内容状态方程的求解
多端口法
1
4.1 线性非常态网络的状态方程的系统编写法
含有纯电容（和电压源）含有纯电容（和电压源）的回路或纯电感（和电流源）或纯电感（和电流源）的割集
病态网络非常态网络
复杂性阶数＝状态变量个数
一组能够描述网络动态特性的独立且充分的状态变量的个数
＝电感数＋电容数－病态回路数－病态割集数电感数＋电容数－病态回路数－假设（假设（1）网络不含受控源或负元件；网络不含受控源或负元件；每个二端元件（和独立电压、电流源）（2）每个二端元件（R 、L 、C 和独立电压、电流源）选作为一条支路
具体参数见P111－112
6
系统法建立状态方程步骤：系统法建立状态方程步骤： (1）将支路按规定排列、编号定方向；将支路按规定排列、编号定方向； (2）作相应线图G ，并画出标准树；并画出标准树； (3）列写基本割集矩阵及其各分块矩阵；列写基本割集矩阵及其各分块矩阵； L (4) 求矩阵 Gt 、Gl 、 t 、Cl 、L t t 、 ll 、Ltl 、 lt 、 R 、 G ； C L (5) 由式（6-37）、(6-38)、(6-39)、(6-40)、(6-54)、(6-52)、由式（ (6-43)、(6-44)、(6-55) 、(6-53)、( 6-47 ) 、( 6-48 ) ，求式中的各分块矩阵，即获得所需方程。（6-32 ）中的各分块矩阵，即获得所需方程。

第4章网络的状态方程

合集下载