电路-状态方程

§11-6 状态方程一、状态：指在某给定时刻描述网络所需要的一组最少量信息，它连同从该时刻开始的任意输入，便可以确定网络今后的性状。

二、状态变量：描述系统所需要的一组最少量的变量。

三、状态方程：以状态变量为未知量的一组一阶微分方程。

状态变量[,]Tc L X u i =取111CL L L c sC L L c L s du Ci dt diL Ri u u dtdu i dt C di R u i u dt L L L==--+==--+写成矩阵形式.10011C c s L L du u dt C u i di R L dt L L X AX BU ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥--⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦=+标准形式状态变量的选择不唯一, 也可12[,][,]TCC du X x x u dt==取 122212211()C C S C S dx x dtd u du dx R x x u LC RC u u dt LC L LC dt dt==--+++= 写成标准形式()C u t112201011S dx x dt u R dx x LC L LC dt ⎡⎤⎡⎤⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦四、状态方程的列写 1, 直观法1c C du i dt C =对仅含一条电容支路的节点列KCL 方程 1L Ldi u KVL dt L=对仅含一条电感支路的节点列方程例1：列写如下图所示电路的状态方程。

解：选取单一电感回路，如图l 1、l 2所示；状态变量12[,]T L L X i i =取12211112112221211ss L L L di R i u L dtdi R i R i u L dti i i i i +=++==+=整理并消去中间变量i 1、i 2，得1122122225s sL L L L L L d u dt d u dti i i i i i =--+=--+写成标准形式R R 2L21L H1122221251s L L L L d dt u d dt i i i i ⎡⎤⎢⎥⎡⎤--⎡⎤⎡⎤⎢⎥=+⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦⎢⎥⎣⎦例2：列如下图所示电路的状态方程。

t’触发器状态方程T触发器是数字电路中的一个常见元件，经常用于存储一个二进制信号的状态。

在实际应用中，通过改变T触发器的状态可以实现很多有用的功能，例如数据存储、计数器和分频器等。

因此，了解T触发器的工作原理和状态方程对于学习数字电路的基础知识非常重要。

T触发器基本原理T触发器是一种由两个互相反向连接的RS触发器组成的电路。

一个RS触发器有两个输入端：S（Set）和R（Reset），和两个输出端：Q（正输出）和Q'（反输出），RS触发器的状态受到输入信号的控制。

当S和R的输入状态都为低电平时，RS触发器的输出状态不确定。

如果S和R的输入状态同时为高电平，RS触发器的输出状态为“保持（hold）”状态。

当S为低电平，R为高电平时，RS触发器的输出状态为“置1（set）”状态（Q=1，Q'=0）。

反之，当S为高电平，R为低电平时，RS触发器的输出状态为“清零（reset）”状态（Q=0，Q'=1）。

T触发器基本原理与RS触发器类似，只是将RS触发器的S和R输入端合并成为一个T输入端，T的输入端可以有高电平或低电平两种状态。

当T为低电平时，T触发器的输出状态与上一状态（Q(t-1)和Q'(t-1)）保持一致，即Q(t)=Q(t-1)和Q'(t)=Q'(t-1)。

当T为高电平时，T触发器的输出状态与上一状态取反，即Q(t)=1-Q(t-1)和Q'(t)=1-Q'(t-1)。

因此，T触发器可以实现一个简单的二进制计数器，每次T的输入状态由低变高时，输出状态就会翻转一次。

T触发器状态方程T触发器的状态方程可以用逻辑表达式或状态转移图来表示。

逻辑表达式的形式为：Q(t+1) = T(t) ⊕ Q(t)其中“⊕”表示异或运算。

上式表示T触发器在某时刻t的输入信号为T(t)，输出状态为Q(t)，在下一个时刻（t+1）的输出状态为Q(t+1)。

根据T触发器的基本原理，当T为低电平时，Q(t+1)等于Q(t)；当T为高电平时，Q(t+1)等于1-Q(t)。

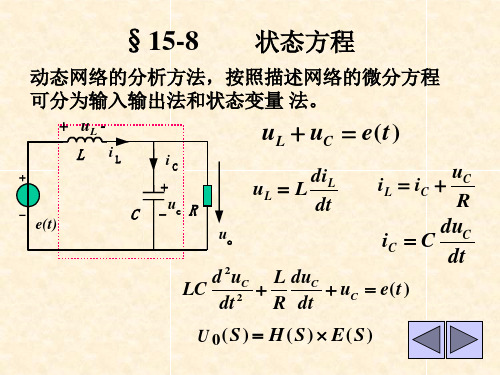
10.1 状态变量和状态方程(1)状态及状态变量的概念状态：电路状态指在任何时刻必需的最少量的信息，它们和自该时刻以后的输入（激励）足以确定该电路此后的性状。

状态变量：描述电路状态的一组变量，这组变量在任何时刻的值表明了该时刻电路的状态。

状态变量的选取方法：电路变量选取不是唯一的，对于动态电路，动态变量的个数与动态元件的个数相同，常取电感中的电流和电容上的电压作为动态变量。

10.1 状态变量和状态方程(2)状态方程图示电路，以电容上的电压和电感中的电流为状态变量列出方程：写成矩阵形式：10.1 状态变量和状态方程状态方程标准形式：——n维状态变量列向量——n维状态变量列向量对时间的一阶导数V——r维输入（激励）列向量B——为nXr阶常数矩阵10.1 状态变量和状态方程(3)输出方程对电路的输出变量列写的方程即为输出方程。

例如，如图示，我们关心的是电流i和R2电阻上的电压，则输出方程为：写成矩阵形式：输出方程的一般形式：式中，X,Y分别是状态变量和输出变量列向量；C,D是常数矩阵。

10.2 状态方程列写方法(1)观察法对简单电路通过观察列写状态方程。

方法是：对含C的结点列写KCL，对含L的回路列写KVL。

如图所示，对结点①列KCL对回路1列KVL:即：写成矩阵形式：10.2 状态方程列写方法(2)叠加法基本思路：用电压源代替电容，用电流源代替电感，然后用叠加定理求电容中的电流和电感中的电压。

如图右上图所示，用电压源替代电容用电流源替代电感后得到右下图。

10.2 状态方程列写方法10.2 状态方程列写方法(3)拓扑法对复杂电路，借助网络图论列写状态方程，称为拓扑法。

拓扑法基本思路：A、将图中的每个元件看成一条支路。

B、选一棵常态树：树支包含的有电压源支路和电容支路和一些必要的电阻支路，不含任何电感支路和电流源支路。

当电路存在由电压源和电容构成的回路以及不存在由电感的电流源构成的割集时，这样的常数树是存在的。

答案10.1解：0<t时，电容处于开路，故V 20k 2m A 10)0(=Ω⨯=-C u由换路定律得：V 20)0()0(==-+C C u u换路后一瞬间，两电阻为串联，总电压为)0(+C u 。

所以m A 5k )22()0()0(1=Ω+=++C u i再由节点①的KCL 方程得：m A5m A )510()0(m A 10)0(1=-=-=++i i C答案10.2解：0<t时电容处于开路，电感处于短路，Ω3电阻与Ω6电阻相并联，所以A3)363685(V45)0(=Ω+⨯++=-i，A 2)0(366)0(=⨯+=--i i LV 24)0(8)0(=⨯=--i u C由换路定律得：V24)0()0(==-+C C u u ，A 2)0()0(==-+L L i i由KVL 得开关电压：V8V )2824()0(8)0()0(-=⨯+-=⨯+-=+++L C i u u答案10.3解：0<t 时电容处于开路，0=i ，受控源源电压04=i ，所以V 6.0V 5.1)69(6)0()0()0(1=⨯Ω+Ω===--+u u u C C>t 时，求等效电阻的电路如图(b)所示。

等效电阻Ω=++-==5)36(4i ii i i u R 时间常数s 1.0i ==C R τ0>t 后电路为零输入响应，故电容电压为：V e 6.0e )0()(10/t t C C u t u --+==τΩ6电阻电压为：V e 72.0)d d (66)(101t Ctu Ci t u -=-⨯Ω-=⨯Ω-=)0(>t答案10.4 解：<t 时电感处于短路，故A 3A 9363)0(=⨯+=-L i ，由换路定律得： A 3)0()0(==-+L L i i求等效电阻的电路如图(b)所示。

(b)等效电阻Ω=+⨯+=836366i R ，时间常数s 5.0/i ==R L τ 0>t 后电路为零输入响应，故电感电流为 A e 3e )0()(2/t t L L i t i --+==τ)0(≥t电感电压V e 24d d )(21t Lti Lt u --==)0(>t Ω3电阻电流为A e 23632133t L u i u i --=Ω+⨯Ω=Ω=Ω3电阻消耗的能量为：W3]e 25.0[1212304040233=-==Ω=∞-∞-∞Ω⎰⎰t t dt e dt i W答案10.5解：由换路定律得0)0()0(==-+L L i i ，达到稳态时电感处于短路，故A 54/20)(==∞L i求等效电阻的电路如图(b)所示。

第7章一阶电路和二阶电路的时域分析状态方程的概念 会写电路的状态方程状态方程√ 状态方程的列写 √ 输出方程的列写 √状态变量的选择 状态方程的求解（时域或频域求解） × 输出方程的求解（时域或频域求解） ×2010/11/1电路 自动化科学与电气工程学院11、状态和状态变量 状态 电路在tk时刻的状态是指在该时刻电路所必须具 有的一组独立完备数据，这组数据不仅反映了tk 时刻以前所有输入对电路的作用效果，而且结 合（tk，t）期间的输入就能够完全确定t时刻电 路的特性。

2010/11/1电路 自动化科学与电气工程学院2状态变量一组独立的网络变量(1)这组变量在t=t0时刻的值和从t=t0开始的输入能唯一 决定这组变量在任何时刻t>t0时的值。

(2) t时刻的这组变量值和t时刻的输入值能唯一决定网 络的任一变量在时刻t的值。

则这组变量称为状态变量,由这组变量构成的集合称为网 络的状态。

通常选独立的电容电压和电感电流作为网络的 状态变量2010/11/1 电路 自动化科学与电气工程学院 32. 状态方程和输出方程tRLiLuCd uC C = iL dtuSuRuLCd uC 1 = iL d 2 uC d uC + RC + uC = uS LC dt C 2 dt dt d iL 1 R 1 = − u C − iL + u S dt L L Ld iL uS = RiL + L + uC dtt >0⎡ d uC ⎤ ⎡ ⎢ dt ⎥ ⎢ 0 ⎢ ⎥=⎢ ⎢ d iL ⎥ ⎢ − 1 ⎢ dt ⎥ ⎢ L ⎣ ⎦ ⎣2010/11/11 ⎤ ⎡0⎤ C ⎥ ⎡ uC ⎤ ⎢ ⎥ ⎥ ⎢ ⎥ + 1 [uS ] R ⎥ ⎣ iL ⎦ ⎢ ⎥ − ⎣L⎦ ⎥ L⎦电路 自动化科学与电气工程学院4⎡ x1 ⎤ ⎡ x1 ⎤ ⎢ x ⎥ = A ⎢ x ⎥ + B [ uS ] ⎣ 2⎦ ⎣ 2⎦状态方程的标准形式：χ=A χ+B ν状态方程是状态向量的一阶微分方程，描述了 电路中有记忆元件的输入－输出关系，体现了 电路的动态特性。