2017年秋八年级数学上册192证明举例(4)沪教版五四制
- 格式:doc
- 大小:625.50 KB
- 文档页数:3

沪教版数学⼋年级上第⼗九章⼏何证明19.2证明举例练习⼀和参考答案数学⼋年级上第⼗九章⼏何证明19.2证明举例(1)⼀、选择题1.如图,AC=AD,CE=ED,则图中全等三⾓形有()A.3对 B.4对 C.5对 D.6对第1题第3题2.⼀个⾓的两边与另⼀个⾓的两边分别平⾏,则这两个⾓的位置关系是()A.相等 B.互补 C.相等或互补; D.互余3.如图,D在AB上,E在AC上,且∠B=∠C,那么补充下列⼀个条件后,仍然⽆法判断△ABE≌△ACD 的是()A.AD=AE B.∠AEB=∠ADC C.BE=CD D.AB=AC4.等腰三⾓形的⼀个⾓是80°,那么另外两个⾓分别是()A.80°、20° B.50°、50° C.80°、80° D.80°、20°或50°、50°5.下列图形中,两个三⾓形全等的是()A. 边长为15cm的两个等边三⾓形B.含60°⾓的两个锐⾓三⾓形C. 腰长对应相等的两个等腰三⾓形D. 有⼀个钝⾓对应相等的两个等腰三⾓形6. 在下列命题中,为假命题的是()A. 两边及其夹⾓对应相等的两个三⾓形全等B. 两⾓及其夹边对应相等的两个三⾓形全等C. 两边及⼀边的对⾓对应相等的两个三⾓形全等D. 三边对应相等的两个三⾓形全等⼆、填空题7. 过⼀点有且直线与已知直线垂直。
8. 等腰三⾓形顶⾓的、底边上的、互相重合。
9. 在⼏何证明过程中,为了化繁为简,常常要利⽤来实现。
10. 在△ABC中,∠ACB=90°,CD⊥AB于D,∠B=38°,则∠ACD= 。
11. 若等腰三⾓形⼀个内⾓为70°,则它⼀腰上的⾼与底边所夹的⾓等于。
12. 如图,BC=AD,只需添加⼀个条件,则△ABC≌△CDA。
第12题第13题第14题第15题13. 如图,已知AB=AD,∠ABC=∠ADC,要证CB=CD,需添置辅助线是。

19.2证明举例一、解答题1.(2020·上海市静安区实验中学初二课时练习)已知:如图点D在AB上,E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C,求证:BD=CE.【答案】见解析【解析】由两角和夹边ASA即可得出∠ABE∠∠ACD,由全等三角形的性质可到AE=AD,进而可得出结论BD=CE.证明:在∠ABE和∠ACD中B CA A AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,所以∠ABE∠∠ACD(ASA),所以AD=AE,因为AB=AC,所以AB-AD=AC-AE即:BD=CE,【点睛】本题主要考查了全等三角形的判定及性质问题,关键是由两角和夹边得出∠ABE∠∠ACD.2.(2020·上海市静安区实验中学初二课时练习)已知:如图所示ABC,BE,CD相交于O,AB=AC,AD=AE(1)求证:OD=OE(2)联结DE,求证:DE//BC.【答案】(1)见解析;(2)见解析≅,再由全等三角形对应边、对应角相等解题即可;【解析】(1)根据SAS证明ADC AEB≅,最后根据全等三角形(2)先根据AB=AC,整理出BD、EC的数量关系,再由AAS证明BDO CEO对应边相等的性质解题即可.(1)证明:在ADC和AEB△中AB=AC;∠A=∠A;AD=AE,≅所以ADC AEB所以∠ABE=∠ACD,又因为AD=AE,所以BD=CE , 在BDO △和CEO 中 BD=EC ∠ABE=∠ACD ∠DOB=∠EOC 所以BDO CEO ≅ 所以OD=OE (2)证明:AD AE AB AC ==,AD AEAB AC∴=A A ∠=∠ADE ABC ∴ADE ABC ∴∠=∠//DE BC ∴【点睛】本题考查全等三角形的判定与性质、相似三角形的判定与性质,是重要考点,难度一般,掌握相关知识是解题关键.3.(2020·上海市静安区实验中学初二课时练习)已知:如图,在∠ABC中,∠A∠∠ABC∠∠ACB=3∠4∠5,BD,CE分别是边AC,AB上的高,BD,CE相交于H,求∠BHC的度数.【答案】135°【解析】先设∠A=3x∠∠ABC=4x∠∠ACB=5x,再结合三角形内角和等于180°,可得关于x的一元一次方程,求出x,从而可分别求出∠A∠∠ABC∠∠ACB,在∠ABD中,利用三角形内角和定理,可求∠ABD,再利用三角形外角性质,可求出∠BHC∠解:∠在∠ABC中,∠A∠∠ABC∠∠ACB=3∠4∠5∠故设∠A=3x∠∠ABC=4x∠∠ACB=5x∠∠在∠ABC中,∠A+∠ABC+∠ACB=180°∠∠3x+4x+5x=180°∠解得x=15°∠∠∠A=3x=45°∠∠BD∠CE分别是边AC∠AB上的高,∠∠ADB=90°∠∠BEC=90°∠∠在∠ABD中,∠ABD=180°-∠ADB-∠A=180°-90°-45°=45°∠∠∠BHC=∠ABD+∠BEC=45°+90°=135°∠【点睛】本题利用了三角形内角和定理、三角形外角的性质.解题关键是熟练掌握:三角形三个内角的和等于180°,三角形的外角等于与它不相邻的两个内角之和.4.(2020·上海市静安区实验中学初二课时练习)如图,AB=AC,E是AD上的一点,∠BAE=∠CAE.求证:∠EBD=∠ECD.【答案】见解析【解析】先证明∠ABD∠∠ACD ,得到∠ADB=∠ADC ,BD=CD ,再证明∠BDE∠∠CDE ,问题得证.证明:在∠ABD 和∠ACD 中AB AC BAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩∠∠ABD∠∠ACD ,∠∠ADB=∠ADC ,BD=CD ,在∠BDE 和∠CDE 中DE DE EDB EDC BD CD =⎧⎪∠=∠⎨⎪=⎩∠∠BDE∠∠CDE , ∠∠EBD=∠ECD . 【点睛】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定定理并根据题意灵活选择方法是解题关键.5.(2020·仪征市第三中学初二月考)如图,点E∠F 在BC 上,BE=CF∠AB=DC∠∠B=∠C∠AF 与DE 交于点G ,求证:GE=GF∠【答案】证明见解析. 【解析】求出BF=CE ,根据SAS 推出∠ABF∠∠DCE ,得对应角相等,由等腰三角形的判定可得结论. ∠BE=CF∠∠BE+EF=CF+EF∠ ∠BF=CE∠在∠ABF 和∠DCE 中AB DC B C BF CE =⎧⎪∠=∠⎨⎪=⎩∠ ∠∠ABF∠∠DCE∠SAS∠∠ ∠∠GEF=∠GFE∠ ∠EG=FG∠【点睛】本题考查了全等三角形的判定与性质,等腰三角形的判定,熟练掌握三角形全等的判定方法是解题的关键.6.(2020·全国初一课时练习)如图,现有以下3个论断://BD EC ;D C ∠=∠;A F ∠=∠.(1)请以其中两个为条件,另一个为结论组成命题,你能组成哪几个命题? (2)你组成的命题是真命题还是假命题?请你选择一个真命题加以证明. 【答案】(1)见解析;(2)见解析.【解析】(1)分别以其中两个作为条件,第三个作为结论依次交换写出即可;(2)根据平行线的判定和性质对(1)题的3个命题进行证明即可判断其真假.解:(1)由//BD EC ,D C ∠=∠,得到A F ∠=∠;由//BD EC ,A F ∠=∠,得到D C ∠=∠; 由A F ∠=∠,D C ∠=∠,得到//BD EC ; 故能组成3个命题.(2)由//BD EC ,D C ∠=∠,得到A F ∠=∠,是真命题.理由如下://BD EC ,ABD C ∴∠=∠. D C ∠=∠,∠ABD D ∠=∠, //AC DF ∴,A F ∴∠=∠.由//BD EC ,A F ∠=∠,得到D C ∠=∠,是真命题.理由如下://BD EC ,ABD C ∴∠=∠. A F ∠=∠,//AC DF ∴,,D ABD ∴∠=∠D C ∴∠=∠.由A F ∠=∠,D C ∠=∠,得到//BD EC ,是真命题.理由如下: ∠A F ∠=∠,//AC DF ∴,D ABD ∴∠=∠.D C ∠=∠,ABD C ∴∠=∠,//BD EC ∴.【点睛】本题考查了命题与定理的知识和平行线的判定与性质,属于基础题型,熟练掌握平行线的判定与性质是解题的关键.7.(2020·四川前锋·初三其他)如图,点A 、F 、C 、D 在一条直线上,AB DE ∥,AB DE =,AF DC =.求证:BC EF ∥.【答案】见解析.【解析】由全等三角形的性质SAS 判定∠ABC∠∠DEF ,则对应角∠ACB=∠DFE ,故证得结论.∠AB DE ∥, ∠A D ∠=∠. ∠AF DC =, ∠AC DF =.在ABC △与DEF 中,AB DE A D AC DF =⎧⎪∠=∠⎨⎪=⎩, ∠ABC △∠DEF (SAS ). ∠ACB DFE ∠=∠.∠BC EF ∥. 【点睛】本题考查全等三角形的判定和性质、平行线的性质等知识,解题的关键是正确寻找全等三角形全等的条件. 8.(2020·广西北流·初三学业考试)如图,在Rt ABC △中,90ABC ∠=︒,点D 在边AB 上,使DB BC =,过点D 作EF AC ⊥,分别交AC 于点E ,交CB 的延长线于点F .求证:AB BF =.【答案】详见解析【解析】根据EF AC ⊥得出90F C ∠+∠=︒,再根据90A C ∠+∠=︒,故A F ∠=∠,证明FBD ∠ABC 即可证明AB BF =.∠EF AC ⊥,∠90F C ∠+∠=︒.∠90A C ∠+∠=︒,∠A F ∠=∠.在FBD 和ABC 中,90A FFBD ABC BD BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,∠FBD ∠ABC (AAS ),∠AB BF =. 【点睛】本题考查了直角三角形两锐角互余以及三角形全等的判定和性质,熟练掌握直角三角形两锐角互余以及三角形全等的判定和性质是解题的关键.9.(2019·全国初二课时练习)如图,在∠ABC 中,AB=AC ,D 点在BA 的延长线上,点E 在AC 上,且AD=AE ,DE 的延长线交BC 于点F ,求证:DF∠BC .【答案】见解析证明.【解析】试题分析:过A作AM∠BC于M,根据等腰三角形“三线合一”的性质得出∠BAC=2∠BAM,由三角形外角的性质及等边对等角的性质得出∠BAC=2∠D,则∠BAM=∠D,根据平行线的判定得出DF∠AM,进而得到DF∠BC.试题解析:证明:如图,过A作AM∠BC于M,∠AB=AC,∠∠BAC=2∠BAM,∠AD=AE,∠∠D=∠AED,∠∠BAC=∠D+∠AED=2∠D,∠∠BAC=2∠BAM=2∠D,∠∠BAM=∠D,∠DF∠AM,∠AM∠BC,∠DF∠BC.考点:等腰三角形的性质..10.(2020·玉山县南山乡中学月考)如图,点A,B,C在同一直线上,点E在BD上,且ABD EBC()1求证:AC BD ⊥;()2判断直线AD 与直线CE 的位置关系,并说明理由.【答案】(1)见解析;(2)垂直,理由见解析【解析】(1)根据全等三角形的对应角相等和平角的定义解答;(2)根据全等三角形的对应角相等和三角形内角和定理进行解答.()1证明:∠ABD EBC ≅,ABD EBC ∠=∠∴.又A ,B ,C 在同一条直线上,90EBC EBA ∴∠=∠=,即AC BD ⊥.()2解:直线AD 与直线CE 垂直.理由:延长CE 交AD 于F ,如图所示,ABD EBC ≅, D C ∴∠=∠.在Rt ABD △中,90A D ∠+∠=,则A C90∠+∠=,∠90∠=,AFC⊥.即CE AD【点睛】本题考查的是全等三角形的性质,掌握全等三角形的对应边相等,对应角相等是解答的关键.11.(2020·荆州市实验中学月考)如图,∠ABE和∠CBF有公共顶点B,且满足AB=CB,EB=FB,AB∠BC,BE∠BF,AE和CF交于点D.(1)求证:∠ABE∠∠CBF;(2)求证:AE∠CF.【答案】(1)见解析;(2)见解析【解析】(1)由已知可得:∠ABE=∠FBC,从而可得∠ABE∠∠CBF;(2)记AE与BC交于点H,则由(1)和已知可得∠A=∠C,∠CHD=∠AHB,再由三角形内角和定理可以得到∠CDH=∠CBA=90°,从而可以证得AE∠CF.(1)由AB∠BC,BF∠BE可知:∠ABC=∠EBF=90°∠∠ABC+∠CBE=∠EBF+∠CBE即∠ABE=∠FBC在∠ABE和∠CBF中:ABE CBF EB FB ⎪∠=∠⎨⎪=⎩∠∠ABE∠∠CBF (SAS ) (2)由(1)知:∠ABE∠∠CBF ∠∠A =∠C记AE 与BC 交于点H ,则:∠AHB =180°-∠ABC -∠A =90°-∠A 又∠∠CHD =∠AHB =90°-∠A ∠∠C +∠CHD =∠C +90°-∠A =90° ∠∠CDH =180°-90°=90° ∠AE∠CF 【点睛】本题考查三角形全等的应用,综合运用三角形全等的判定和性质、三角形内角和定理求证是解题关键. 12.(2020·湖南渌口·初二期末)如图,BD ∠CE 分别是ABC 的高,且BE CD =,求证:Rt BEC Rt CDB ≅∠【答案】证明见解析.【解析】根据高的定义求出∠BEC=∠CDB=90°,根据全等三角形的判定定理HL 推出即可;证明:∠BD ∠CE 分别是ABC 的高, ∠90BEC CDB ∠=∠=∠ 在Rt BEC 和Rt CDB 中,BE CD⎨=⎩∠ ∠()Rt BEC Rt CDB HL ≅∠ 【点睛】此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.13.(2020·剑阁县公兴初级中学校初二月考)如图,AD 是ABC 的角平分线,点E 在BC 的延长线上,求证:122B ∠+∠=∠.【答案】见解析【解析】根据三角形的外角性质得出∠1=∠B+∠BAC ,∠2=∠B+∠BAD ,再利用角平分线的定义转化证明即可.证明:∠∠1=∠B+∠BAC ,∠2=∠B+∠BAD , ∠AD 是∠ABC 的角平分线, ∠∠BAC=2∠BAD ,∠∠B+∠1=∠B+∠B+∠BAC=2∠B+2∠BAD=2∠2. 【点睛】此题考查三角形外角的性质,关键是根据三角形的外角性质得出∠1=∠B+∠BAC ,∠2=∠B+∠BAD . 14.(2020·安徽临泉·初二期末)如图,在ABC ∆和DEF ∆中,B 、E 、C 、F 在同一直线上,下面有四个条件:∠AB DE =;∠AC DF =;∠//AB DE ;∠BE CF =.请你从中选三个作为题设,余下的一个作为结论,写出一个真命题,并加以证明. 解:我写的真命题是:已知:____________________________________________; 求证:___________.(注:不能只填序号) 证明如下:【答案】已知:如图,在∠ABC 和∠DEF 中,B 、E 、C 、F 在同一直线上,AB=DE ,AC=DF ,BE=CF.求证:AB∠DE.证明见解析.或已知:如图,在∠ABC 和∠DEF 中,B 、E 、C 、F 在同一直线上,AB=DE ,AB∠DE ,BE=CF .求证:AC=DF .证明见解析.【解析】由BE=CF∠BC=EF ,所以,由∠∠∠,可用SSS∠∠ABC∠∠DEF∠∠ABC=∠DEF∠ AB∠DE ;由∠∠∠,可用SAS∠∠ABC∠∠DEF∠AC=DF ;由于不存在ASS 的证明全等三角形的方法,故由其它三个条件不能得到1或4.解:将∠∠∠作为题设,∠作为结论,可写出一个正确的命题,如下:已知:如图,在∠ABC 和∠DEF 中,B 、E 、C 、F 在同一直线上,AB=DE ,AC=DF ,BE=CF . 求证:AB∠DE .证明:在∠ABC 和∠DEF 中, ∠BE=CF , ∠BC=EF.又∠AB=DE ,AC=DF , ∠∠ABC∠∠DEF (SSS ) ∠∠ABC=∠DEF . ∠ AB∠DE.将∠∠∠作为题设,∠作为结论,可写出一个正确的命题,如下:已知:如图,在∠ABC 和∠DEF 中,B 、E 、C 、F 在同一直线上,AB=DE ,AB∠DE ,BE=CF . 求证:AC=DF .证明:∠AB∠DE,∠∠ABC=∠DEF. 在∠ABC 和∠DEF 中 ∠BE=CF ,∠BC=EF.又∠AB=DE,∠ABC=∠DEF,∠∠ABC∠∠DEF(SAS),∠AC=DF.【点睛】本题考查命题与定理、全等三角形的判定和性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于中考常考题型.15.(2020·上虞市实验中学初二月考)如图:AB=CD,AE=DF,CE=FB.求证:AF=DE.【答案】见解析.【解析】先根据CE=FB得到CF=BE,然后利用“边边边”证明∠ABE和∠DCF全等,根据全等三角形对应角相等可得∠B=∠C,再利用“边角边”证明∠ABF和∠DCE全等,然后根据全等三角形对应边相等得证.∠CE=FB,∠CE+EF=FB+EF,即CF=BE,在∠ABE和∠DCF中,AB CD AE DF CF BE ⎧⎪⎨⎪⎩===∠∠ABE∠∠DCF(SSS),∠∠B=∠C,在∠ABF和∠DCE中AB CDB C CE FB ⎧⎪∠∠⎨⎪⎩===∠∠ABF∠∠DCE(SAS),∠AF=DE.【点睛】本题考查了全等三角形的判定与性质,根据CE=FB证明得到CF=BE是解题的关键,注意本题需要两次证明三角形全等.16.(2020·江苏海安·月考)如图,AD=CB,AE∠BD,CF∠BD,E、F是垂足,AE=CF.求证:(1)AB=CD(2)AB//CD.【答案】(1)见解析;(2)见解析【解析】(1)利用HL得到直角三角形ADE与直角三角形CBF全等,利用全等三角形的对应边相等得到DE=BF,可得DF=BE,利用SAS得到三角形AEB与三角形CFD全等,利用全等三角形的对应边相等即可得证;(2)由全等三角形的对应角相等得到一对内错角相等,利用内错角相等两直线平行即可得证.证明:(1)⊥⊥,CF BDAE BDAEB CFD AED CF∴∠=∠=∠=∠=︒B90==,AD CBAE CF∴∆≅∆()Rt ADE CBF HL∠DE=BF∴-=-BD BD BFDE∴=BE DF=∠AEB CFD∠=∠,AE CF∠ABE CDF∆≅∆(SAS)∠AB=CD;∆≅∆(2)∠ABE CDFABE CDF∠∠=∠∴AB CD//【点睛】本题考查全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.17.(2020·上虞市实验中学初二月考)已知∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P放在射线OM上滑动,两直角边分别与OA、OB交于C、D,PC和PD有怎样的数量关系,证明你的结论.【答案】PC=PD,证明见解析【解析】作PE∠OA,PF∠OB,垂足分别为E、F,易证∠ PEO∠∠PFO,得出∠CPE=∠DPF,再证∠PEC∠∠PFD 即可.解:PC=PD证明:作PE∠OA,PF∠OB,垂足分别为E、F.则有∠PEC=∠PFD=90°即∠PEO=∠PFD=90°∠OM平分∠AOB∠∠POE=∠POF于是在∠PEO和∠PFO中∠PEO PFOPOE POFPO PO∠=∠⎧⎪∠=∠⎨⎪=⎩∠ ∠ PEO∠∠PFO(AAS)∠ PE=PF(全等三角形的对应边相等)∠ ∠CPD= 90 ° 即∠CPE+∠EPD=90°易知∠ EPF= 90 ° 即∠ DPF+∠EPD=90°∠ ∠CPE=∠DPF于是在∠PEC和∠PFD中∠PEC PFDCPE DPFPE PF∠=∠⎧⎪∠=∠⎨⎪=⎩∠ ∠PEC∠∠PFD(AAS)∠ PC=PD(全等三角形的对应边相等)18.(2020·湖北红安·初二月考)如图1,已知∠ABC中,AB=BC=1,∠ABC=90°,把一块含30°角的直角三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),将直角三角板DEF绕D点按逆时针方向旋转.(1)在图1中,DE交边AB于M,DF交边BC于N,证明:DM=DN;(2)在这一旋转过程中,直角三角板DEF与∠ABC的重叠部分为四边形DMBN,请说明四边形DMBN的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积;(3)继续旋转至如图2的位置,延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立,请给出证明;若不成立,请说明理由.【答案】(1)详情见解析;(2)四边形DMBN面积不发生变化,面积为14;(3)仍然成立,证明见解析.【解析】(1)连接BD,求出BD=DC,∠MDB=∠CDN,∠C=∠ABD,根据ASA证明∠MBD∠∠NCD,进而求证即可;(2)根据全等得出∠MBD与∠NCD面积相等,求出四边形DMBN的面积等于∠BDC的面积,进而求解即可;(3)连接BD,求出BD=DC,∠MDB=∠CDN,∠C=∠ABD,根据ASA证明∠MBD∠∠NCD,进而求证即可.(1)如图1,连接BD.∠在Rt∠ABC中,AB=BC,AD=DC,∠BD=DC=AD,∠BDC=90°,∠∠ABD=∠C=45°,∠∠MDB+∠BDN=90°,∠CDN+∠BDN=90°∠∠MDB=∠NDC,在∠MBD与∠NCD中,∠∠MDB=∠NDC,BD=DC,∠MBD=∠C,∠∠MBD∠∠NCD,∠DM=DN.(2)四边形DMBN面积不发生变化.由(1)得∠MBD∠∠NCD,∠S∠MBD=S∠NCD,∠四边形DMBN面积=S∠DMB+S∠BDN= S∠CND+ S∠BDN=12S∠ABC=14.∠3∠DM=DN仍然成立.如图2,连接BD,∠在Rt∠ABC中,AB=BC,AD=DC,∠DB=DC,∠BDC=90°,∠∠DCB=∠DBC=45°,∠∠DBM=∠DCN=135°,∠∠NDC+∠CDM=90°,∠BDM+∠CDM=90°,∠∠CDN=∠BDM,在∠CDN与∠BDM中,∠∠CDN=∠BDM,DC=DB,∠DCN=∠DBM,∠∠CDN∠∠BDM,∠DM=DN.【点睛】本题主要考查了三角形旋转问题与全等三角形的综合运用,熟练掌握相关概念是解题关键.。


19.2 证明举例(第4课时)教学目标:1、通过证明举例的学习和实践,懂得演绎推理的一般规则,初步掌握规X的表达格式;了解证明之前进行分析的基本思路。
2、能利用全等三角形的判定与性质、等腰三角形的判定与性质来证明有关线段相等、角相等的简单问题。
3、了解添置辅助线的基本方法,会添置常见的辅助线。
4、了解文字语言、图形语言、符号语言三种数学语言形态。
教学重点:分析基本思路,演绎推理的规X表达格式。
教学难点:辅助线的添加。
教学过程:1.例题讲解例题11 已知:如图,点D在边BC上,BD=CD, ∠1=∠2.求证: AB=AC.证明:延长AD到点E,使DE=AD,联结CE.在△ABD与△ECD中,BD=CD(已知)∠ADB=∠EDC(对顶角相等),AD=ED(所作),∴△ABD≌△ECD(S.A.S).得EC=AB, ∠E=∠1(全等三角形的对应边相等、对应角相等).又∵∠1=∠2(已知),∴∠E=∠2(等量代换)得EC=AC(等角对等边) ∴AB=AC(等量代换).△ACD的中线AD,这为图形的旋转提AD,可作出△ABD关于点D对称的图形.这种添辅助线的方法,在证明直角三角形斜边上的中线的定理时也要用到,本例是一个铺垫.例12 已知:如图,在Rt△ABC中, ∠BAC=90°.点D在BC上,AD=AB.求证: ∠BAD=2∠C.证明:过点A作AH⊥BC,垂足为点H∵AD=AB(已知),∴∠BAD=2∠BAH(等腰三角形的三线合一).在△ABC中,∵∠BAC+∠B+∠C=180°(三角形的内角和等于180°),又∵∠BAC=90°(已知),∴∠B+∠C=90°同理∠BAH+∠B=90°∴∠BAH=∠C(同角的余角相等).∴∠BAD=2∠C(等量代换).说明:本例要证明两角之间的倍半关系,利用了等腰三角形的三线合一这个基本图形,转化为证两角相等,而证两角相等利用了“同角的余角相等”.以前证明两个角相等,主要考虑利用全等三角形的性质,本例有助于学生拓宽思路.。
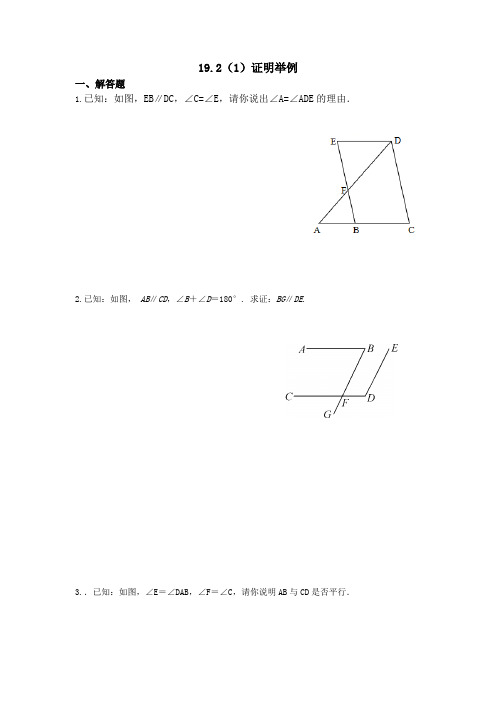
19.2(1)证明举例一、解答题1.已知:如图,EB∥DC,∠C=∠E,请你说出∠A=∠ADE的理由.2.已知:如图, AB∥CD,∠B+∠D=180°. 求证:BG∥DE.3..已知:如图,∠E=∠DAB,∠F=∠C,请你说明AB与CD是否平行.4. 已知:如图, AB=AC,AE平分∠DAB. 求证:AE∥BC.5. 已知:如图,点C、D在AB上,AC=BD,DF∥CE,DF=CE. 求证:BE∥AF.6. 已知:如图, AB∥CD,∠1=∠2. 求证:AC∥BD.二、提高题7.已知:如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.19.2(2)证明举例一、解答题1.已知:如图,点B、E、C、F在同一直线上,AB∥DE,且AB=DE,BE=CF.求证:∠A=∠D.2.已知:如图,点E在△ABC的外部,点D在BC边上,DE交AC于点F,∠1=∠2=∠3,AC=AE.求证:AB=AD.3. 已知:如图, AB=AC,BE=CD. 求证:∠B=∠C.4. 已知:如图, AB=AC,E是AC上任意一点,ED⊥BC,垂足为D,延长DE交BA的延长线于点F. 求证:AE=AF.5. 已知:如图,点D、E在BC上,AB=AC,AD=AE. 求证:BD=CE.二、提高题6.已知:如图,点E为四边形ABCD外一点,联结EB、EA、ED、EC,其中EA、ED与BC交点分别为M、N,且AD∥BC,AE=DE,BE=CE.求证:AB=DC.19.2(3)证明举例一、解答题1.已知:如图,AD是BC上的中线,且BE∥CF.求证: DF=DE.2.已知:如图,AD、BC相交于点O,OA=OD,OB=OC,点E、F在直线AD上,∠ABE=∠DCF.求证:BE‖CF.3. 如图,已知:点C在线段AB上,△ACD和△BCE都是等边三角形,AE交DC于M,BD交CE于N. 求证:MN∥AB.4. 已知:如图, E是BC上一点,AB=EC,∠B=∠C=90°,AE⊥ED. 求证:AE=DE.5. 已知:如图,∠ACB=∠DBC=90°,E是BC上一点,DE⊥AB于点F,AB=DE. 求证:△BDC是等腰直角三角形.二、提高题6. 已知:如图,在△ABC中,EF∥BC,∠1=∠2,D是EF中点。

证明举例 一、授课目的与考点分析:【知识结构框图表】证明中的分析、解题的思路证明举例 几何证明中常用的证明方法添辅助线二、授课内容:【例题1】点D 、E 在△ABC 的边BC 上,AB =AC ,AD =AE 求证:BD =CE几何证明中常用的证明方法证两直线平行——利用平行线的性质和判定;利用平行线的判断定理及其推论来证,这是证明两直线平行最基本的方法(关键是找出同位角、内错角的相等关系或同旁内角的互补关系)证两线段相等——利用三角形全等的性质和判定、利用等腰三角形的性质和判定:(1)如果两线段分别在两个三角形中,那么可证这两个三角形全等(有时可能缺少直接条件,要证两次全等)(2)有时两线段分别在两个三角形中,但这两个三角形不全等,那么可添辅助线构造全等三角形来证。
常添的辅助线有:平行线、垂线、中线、连结线段等(3)如果两线段是一个三角形的两边,可证它们所对的角相等(等角对等边)(4)证明两条线段都等于第三条线段(即以第三条线段为媒介)证两角相等——利用三角形全等的性质和判定、利用等腰三角形的性质和判定:证两直线互相垂直——利用垂直的定义、利用等腰三角形三线合一的性质*5、证一线段等于另一线段的2倍或一半——利用加倍法或拆分法,常常要作辅助线。
【例题2】如图所示,已知∠1=∠2,AB 平分∠DAB,试说明DC ∥AB.D CB A21AB C D E【例题3】已知:如图,BE和CF是△ABC的高线,BE=CF,H是CF、BE的交点.求证:HB=HC 【例题4】△ABC中,AB=AC,PB=PC.求证:BD=CD且AD⊥BC添辅助线由于证明的需要,可以在原来的图上添画一些线,即添加辅助线来完成一些几何证明,辅助线通常画成虚线。
三角形证明题中常见在辅助线做法:利用三角形的主要线段构造全等三角形○1中线:倍长中线法如图,在△ABC中,AD为BC边上的中线。
延长AD到E,使DE=AD,连接CE。
结论:△ABD≌△ECD,∠1=∠E,∠B=∠2,EC=AB,CE∥AB。