氢原子轨道的角度分布图
- 格式:pptx
- 大小:1.08 MB
- 文档页数:12

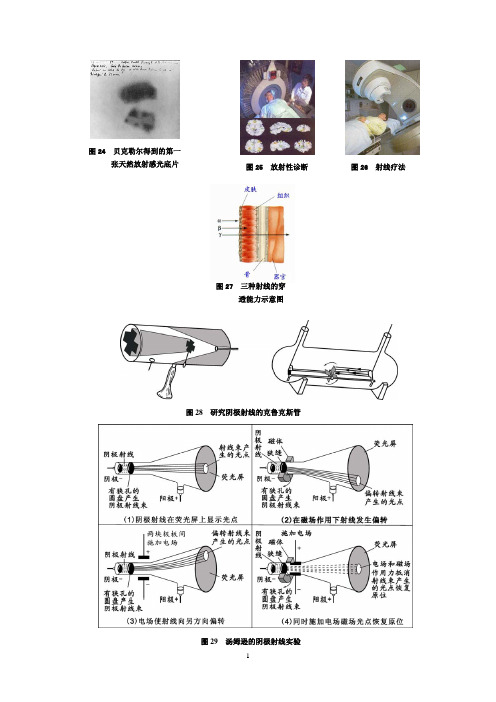
图24 贝克勒尔得到的第一张天然放射感光底片图25 放射性诊断图26 射线疗法图27 三种射线的穿透能力示意图图28 研究阴极射线的克鲁克斯管图29 汤姆逊的阴极射线实验图30密立根的油滴实图31 粒子的相对大小图32 原子核和中子的组成示意图图33 北京正负电子对撞机的电子束流输运线 图34 一种失败的原子模型 图35光电效应图36 可见光、X 射线和电子束 得到相似的衍射图图37 球极坐标与直角坐标的关系图38 氢原子波函数的径向分布 图39 p Z 轨道的角度分布图图40 s 、p 、d 状态的波函数角度分布图图41 s 、p 、d 状态的电子云角度分布图图42 氢原子光谱的产生图43 锂原子光谱图44锂原子能级图图45Herzborg能级图46 外层电子的能量与原子序数的关系图47 从各种内层轨道移去电子所需的能量与原子序数的关系图48 原子轨道能量与原子序数的关系图49 Devauit能级图图50 Latter的原子轨道能量与原子序数图51Latter 的原子轨道能量与原子序数关系图图52用改进的Slater 近似计算求出的原子轨道能量与原子序数的关系 (能量不完全按标度,但交点则按照计算结果) 图53 价层电子对内层电子壳层 的穿透示意图图54 氢原子各种状态的径向分布图图563d和4s对1s22s22p63s23p6原子实的穿透图553d和4s对1s22s2原子实的穿透图图573d和4s原子轨道的径向分布的比较图58屏蔽效应和穿透效应的关系图59Ti原子失去电子成为Ti2+离子时3d和4s能级次序的变化示意。


第二节氢原子的波函数氢原子的第二个四分之一氢原子的波函数是所有原子中最简单的原子。
它的原子核外只有一个电子。
移动到原子核外的电子的势能只取决于检查它的吸引力,它的薛定谔?丁格方程可以精确求解。
此外,类氢离子,例如氦离子和锂离子,可以被精确地解决。
2++为了方便地解决这个问题,用直角坐标表示的ψ(x,y,z)应由用球面极坐标表示的ψ(r,θ,φ)代替。
两者之间的关系如图8-3所示:r代表P点与原点之间的距离,θ、φ称为方位角。
x = r sinθcosφy = r sinθsinφz= r cosθ波函数ψn,l,m(r,θ,φ)和它们相应的氢原子能量列于表8-1图8-3笛卡儿坐标被转换成球面极坐标表8-1氢原子的一些波函数和它们的能量轨道1s ψn,l,m(r,θ,φ) R n,l (r) A1e-Br Y l,m (θ,Phi)能量/j-2.18310-18a1e-Br-2.18310-18/222 sa 2re-Br/2a 2re-Br/2-2。
量子力学借用了玻尔的“原子轨道”的概念,仍然称波函数为“原子轨道”,但是它们的含义是完全不同的。
例如,玻尔认为基态氢原子的原子轨道是半径等于52.9 pm的球形轨道在量子力学中,氢原子基态的原子轨道是波函数ψ1s(r,θ,φ) = A1e-br,其中a1和b是常数,这表明ψ1s随着离核r的距离的变化在任何方位角变化,它代表氢核外1s电子的运动状态,但并不意味着1s电子有确定的运动轨道1s电子的能量为-2.18310焦耳氢核外有许多电子激发态,如ψ2S(R,θ,φ),θ,φ)等。
,相应的能量为-5.45310焦耳-19-18(r,)要求解薛定谔方程的ψ和e,必须满足一定的条件才能使解合理。
因此,在求解过程中必须引入三个量子数n、l和m当这三个参数的值和组合固定时,就确定了波函数。
这三个量子数的极限值及其物理意义如下:主量子数通常用符号n表示。
它可以取任何非零正整数,即1,2,3?n它决定了在最有可能出现在原子核外空间的区域中,电子离原子核的距离,是决定电子能级的主要因素。

第二节氢原子的波函数波函数氢原子是所有原子中最简单的原子,它核外仅有一个电子,电子在核外运动时的势能,只决定于核对它的吸引,它的Schrödinger方程可以精确求解。
能够精确求解的还有类氢离子,如He+、Li2+离子等。
为了求解方便,要把直角坐标表示的ψ(x,y,z) 改换成球极坐标表示的ψ(r,θ,φ),二者的关系如图8-3所示:r表示P点与原点的距离,θ、φ称为方位角。
x = r sinθcosφy = r sinθsinφz = r cosθ解出的氢原子的波函数ψn,l,m(r,θ,φ)及其相应能量列于表8-1中。
图8-3 直角坐标转换成球极坐标表8-1氢原子的一些波函数及其能量轨道ψn,l,m(r,θ, φ)R n,l (r)Y l,m (θ, φ)能量/J1sA1e-B rA1e-B r-2.18×10-182sA2re-B r/2A2re-B r/2-2.18×10-18/222p zA3re-B r/2cosθA3re-B r/2cosθ-2.18×10-18/222p xA3re-B r/2sinθcosφA3re-B r/2sinθcosφ-2.18×10-18/222p yA3re-B r/2sinθsinφA3re-B r/2sinθsinφ-2.18×10-18/22* A1、A2、A3、B均为常数为了方便起见,量子力学借用Bohr N H D理论中“原子轨道”(atomic orbit)的概念,将波函数仍称为原子轨道(atomic orbital),但二者的涵义截然不同。
例如:Bohr N H D认为基态氢原子的原子轨道是半径等于52.9 pm的球形轨道。
而量子力学中,基态氢原子的原子轨道是波函数ψ1S(r,θ,φ)=A1e-Br,其中A1和B均为常数,它说明ψ1S在任意方位角随离核距离r改变而变化的情况,它代表氢原子核外1s电子的运动状态,但并不表示1s电子有确定的运动轨道。

径向分布函数、角度分布函数电子云图形的绘制1.目的要求(1) 绘制波函数及其各种分布以及电子云的图像,观察各种函数的分布情况。
(2) 了解计算机绘图方法。
2.基本原理(1) 程序原理:本程序可绘制类氢原子的径向分布函数,角度分布函数及原子轨道、杂化轨道和分子轨道等电子几率密度图,绘制过程中的各函数形式列于下列各表中。
式中 ,n 为主量子数, =0.0529nm ,为波尔半径, Z 是有效核电荷,由Slater 规则计算得到的周期表中前四个周期元素的有效核电荷列于表Ⅱ-24-1中,下面简要叙述对各类图形的处理方案。
①径向分布函数图:径向分布函数D(r)=r 2R 2(r)反映了电子的几率随半径r 的分布情况, D(r)dr 代表半径r 到r+dr 两个球壳夹层内找到电子的几率。
其中R(r)为类氢原子的径向函数,本程序所采用的径向函数R(r)分别列于表Ⅱ-24-2中。
②角度分布函数图:波函数的角度部分 以及角度分布函数 表示同一球面不同方向上 或 的相对大小,本程序所采用的角度函数分别列于表Ⅱ-24-3中。
322232,),(,,,,sp d sp yz xz z z z Y Y f f f p p 角度分布图是画的X-Z 平面的截面图,其余角度分布图都是画的X-Y 平面的截面图。
角度分布函数图中,凡轨道形状相同,而仅方向不同者,则仅绘出一个图形作为代表。
2na Zr=ρ0a ),,(φθψr nlm ),(φθψlm ),(2φθψlm ),,(φθψr nlm ),,(2φθψr nlm ),(φθψlm③等电子几率密度图:2),,(φθψr 称为电子几率密度函数,它描述在该轨道中的电子在三维空间的分布情况,为了在平面上表示出这种分布往往采用某一切面上的等值面图,程序按指定的轨道在该切面上逐点计算2ψ的值,及找出2max ψ的最大值,求出相对几率密度2max 2/ψψ=P ,该值在X-Y 平面上是位置坐标(x,y)的函数(对于23z d 轨道是在X-Z 平面),绘图时不是将取值相同的点连成曲线,而是打印一系列符号表示相对几率密度的分布区域。
第二节氢原子的波函数波函数氢原子是所有原子中最简单的原子,它核外仅有一个电子,电子在核外运动时的势能,只决定于核对它的吸引,它的Schrödinge r方程可以精确求解。
能够精确求解的还有类氢离子,如He+、Li2+离子等。
为了求解方便,要把直角坐标表示的ψ(x,y,z) 改换成球极坐标表示的ψ(r,θ,φ),二者的关系如图8-3所示:r表示P点与原点的距离,θ、φ称为方位角。
x = r sinθcosφy = r sinθsinφz = r cosθ解出的氢原子的波函数ψn,l,m(r,θ,φ)及其相应能量列于表8-1中。
图8-3 直角坐标转换成球极坐标表8-1氢原子的一些波函数及其能量轨道ψn,l,m(r,θ, φ)R n,l (r)Y l,m (θ, φ)能量/J1sA1e-B rA1e-B r-2.18×10-182sA2re-B r/2A2re-B r/2-2.18×10-18/222p zA3re-B r/2cosθA3re-B r/2cosθ-2.18×10-18/222p xA3re-B r/2sinθcosφA3re-B r/2sinθcosφ-2.18×10-18/222p yA3re-B r/2sinθsinφA3re-B r/2sinθsinφ-2.18×10-18/22* A1、A2、A3、B均为常数为了方便起见,量子力学借用Bohr N H D理论中“原子轨道” (atomic orbit)的概念,将波函数仍称为原子轨道(atomic orbital),但二者的涵义截然不同。
例如:Bohr N H D认为基态氢原子的原子轨道是半径等于52.9 pm的球形轨道。
而量子力学中,基态氢原子的原子轨道是波函数ψ1S(r,θ,φ)=A1e-Br,其中A1 和B均为常数,它说明ψ1S在任意方位角随离核距离r改变而变化的情况,它代表氢原子核外1s电子的运动状态,但并不表示1s电子有确定的运动轨道。