Wjhx-02-1 原子轨道轨道的空间分布

原子轨道原子轨道（Atomic orbital）是单电子薛定谔方程的合理解ψ（x，y，z)。

若用球坐标来描述这组解，即ψ（r，θ，φ)=R(r)·Y(θ，φ)，这里R(r)是与径向分布有关的函数，称为径向分布函数，用图形描述就是原子轨道的径向分布函数；Y(θ，φ)是与角度分布有关的函数，用图形描述就是角度分布函数。

1简介原子轨道（英语：atomic orbital），又称轨态，是以数学函数描述原子中电子似波行为[1][2]。

此波函数可用来计算在原子核外的特定空间中，找到原子中电子的机率，并指出电子在三维空间中的可能位置[1][3]。

“轨道”便是指在波函数界定下，电子在原子核外空间出现机率较大的区域。

具体而言，原子轨道是在环绕着一个原子的许多电子（电子云）中，个别电子可能的量子态，并以轨道波函数描述。

电子的原子与分子轨道，依照能阶排序现今普遍公认的原子结构是波耳氢原子模型：电子像行星，绕着原子核（太阳）运行。

然而，电子不能被视为形状固定的固体粒子，原子轨道也不像行星的椭圆形轨道。

更精确的比喻应是，大范围且形状特殊的“大气”（电子），分布于极小的星球（原子核）四周。

只有原子中存在唯一电子时，原子轨道才能精准符合“大气”的形状。

当原子中有越来越多电子时，电子越倾向均匀分布在原子核四周的空间体积中，因此“电子云”[4]越倾向分布在特定球形区域内（区域内电子出现机率较高）。

早在1904年，日本物理学家长冈半太郎首度发表电子以类似环绕轨道的方式在原子内运转的想法[5]。

1913年，丹麦物理学家尼尔斯·波耳提出理论，主张电子以固定的角动量环绕着体积极小的原子核运行[6]。

然而，一直到1926年、量子力学发展后，薛定谔方程式才解释了原子中的电子波动，定下关于新概念“轨道”的函数[1][7]。

由于这个新概念不同于古典物理学中的轨道想法，1932年美国化学家罗伯特·马利肯提出以“轨道”（orbital）取代“轨道”（orbit）一词[8]。

原子轨道原子轨道（Atomic orbital）是单电子薛定谔方程的合理解ψ（x，y，z)。

若用球坐标来描述这组解，即ψ（r，θ，φ)=R(r)·Y(θ，φ)，这里R(r)是与径向分布有关的函数，称为径向分布函数，用图形描述就是原子轨道的径向分布函数；Y(θ，φ)是与角度分布有关的函数，用图形描述就是角度分布函数。

1简介原子轨道（英语：atomic orbital），又称轨态，是以数学函数描述原子中电子似波行为[1][2]。

此波函数可用来计算在原子核外的特定空间中，找到原子中电子的机率，并指出电子在三维空间中的可能位置[1][3]。

“轨道”便是指在波函数界定下，电子在原子核外空间出现机率较大的区域。

具体而言，原子轨道是在环绕着一个原子的许多电子（电子云）中，个别电子可能的量子态，并以轨道波函数描述。

电子的原子与分子轨道，依照能阶排序现今普遍公认的原子结构是波耳氢原子模型：电子像行星，绕着原子核（太阳）运行。

然而，电子不能被视为形状固定的固体粒子，原子轨道也不像行星的椭圆形轨道。

更精确的比喻应是，大范围且形状特殊的“大气”（电子），分布于极小的星球（原子核）四周。

只有原子中存在唯一电子时，原子轨道才能精准符合“大气”的形状。

当原子中有越来越多电子时，电子越倾向均匀分布在原子核四周的空间体积中，因此“电子云”[4]越倾向分布在特定球形区域内（区域内电子出现机率较高）。

早在1904年，日本物理学家长冈半太郎首度发表电子以类似环绕轨道的方式在原子内运转的想法[5]。

1913年，丹麦物理学家尼尔斯·波耳提出理论，主张电子以固定的角动量环绕着体积极小的原子核运行[6]。

然而，一直到1926年、量子力学发展后，薛定谔方程式才解释了原子中的电子波动，定下关于新概念“轨道”的函数[1][7]。

由于这个新概念不同于古典物理学中的轨道想法，1932年美国化学家罗伯特·马利肯提出以“轨道”（orbital）取代“轨道”（orbit）一词[8]。

原子的轨道原子轨道（德语：atomorbital；英语：atomic orbital），又称轨态，是以数学函数描述原子中电子似波行为。

此波函数可用来计算在原子核外的特定空间中，找到原子中电子的概率，并指出电子在三维空间中的可能位置。

“轨道”便是指在波函数界定下，电子在原子核外空间出现概率较大的区域。

具体而言，原子轨道是在环绕着一个原子的许多电子（电子云）中，个别电子可能的量子态，并以轨道波函数描述。

现今普遍公认的原子结构是波耳氢原子模型：电子像行星，绕着原子核（太阳）运行。

然而，电子不能被视为形状固定的固体粒子，原子轨道也不像行星的椭圆形轨道。

更精确的比喻应是，大范围且形状特殊的“大气”（电子），分布于极小的星球（原子核）四周。

只有原子中存在唯一电子时，原子轨道才能精准符合“大气”的形状。

当原子中有越来越多电子时，电子越倾向均匀分布在原子核四周的空间体积中，因此“电子云”越倾向分布在特定球形区域内（区域内电子出现概率较高）。

在原子物理学的运算中，复杂的电子函数常被简化成较容易的原子轨道函数组合。

虽然多电子原子的电子并不能以“一或二个电子之原子轨道”的理想图像解释，它的波函数仍可以分解成原子轨道函数组合，以原子轨道理论进行分析；就像在某种意义上，由多电子原子组成的电子云在一定程度上仍是以原子轨道“构成”，每个原子轨道内只含一或二个电子。

历史与命名早在1904年，日本物理学家长冈半太郎首度发表电子以类似环绕轨道的方式在原子内运转的想法。

1913年，丹麦物理学家尼尔斯·波耳提出理论，主张电子以固定的角动量环绕着体积极小的原子核运行。

然而，一直到1926年、量子力学发展后，薛定谔方程式才解释了原子中的电子波动，定下关于新概念“轨道”的函数。

由于这个新概念不同于古典物理学中的轨道想法，1932年美国化学家罗伯特·马利肯提出以“轨道”（orbital）取代“轨道”（orbit）一词。

原子轨道是单一原子的波函数，使用时必须代入n（主量子数）、l（角量子数）、m（磁量子数）三个量子化参数，分别决定电子的能量、角动量和方位，三者统称为量子数。

原子轨道原子轨道（Atomic orbital）是单电子薛定谔方程的合理解ψ（x，y，z)。

若用球坐标来描述这组解，即ψ（r，θ，φ)=R(r)·Y(θ，φ)，这里R(r)是与径向分布有关的函数，称为径向分布函数，用图形描述就是原子轨道的径向分布函数；Y(θ，φ)是与角度分布有关的函数，用图形描述就是角度分布函数。

1简介原子轨道（英语：atomic orbital），又称轨态，是以数学函数描述原子中电子似波行为[1][2]。

此波函数可用来计算在原子核外的特定空间中，找到原子中电子的机率，并指出电子在三维空间中的可能位置[1][3]。

“轨道”便是指在波函数界定下，电子在原子核外空间出现机率较大的区域。

具体而言，原子轨道是在环绕着一个原子的许多电子（电子云）中，个别电子可能的量子态，并以轨道波函数描述。

电子的原子与分子轨道，依照能阶排序现今普遍公认的原子结构是波耳氢原子模型：电子像行星，绕着原子核（太阳）运行。

然而，电子不能被视为形状固定的固体粒子，原子轨道也不像行星的椭圆形轨道。

更精确的比喻应是，大范围且形状特殊的“大气”（电子），分布于极小的星球（原子核）四周。

只有原子中存在唯一电子时，原子轨道才能精准符合“大气”的形状。

当原子中有越来越多电子时，电子越倾向均匀分布在原子核四周的空间体积中，因此“电子云”[4]越倾向分布在特定球形区域内（区域内电子出现机率较高）。

早在1904年，日本物理学家长冈半太郎首度发表电子以类似环绕轨道的方式在原子内运转的想法[5]。

1913年，丹麦物理学家尼尔斯·波耳提出理论，主张电子以固定的角动量环绕着体积极小的原子核运行[6]。

然而，一直到1926年、量子力学发展后，薛定谔方程式才解释了原子中的电子波动，定下关于新概念“轨道”的函数[1][7]。

由于这个新概念不同于古典物理学中的轨道想法，1932年美国化学家罗伯特·马利肯提出以“轨道”（orbital）取代“轨道”（orbit）一词[8]。

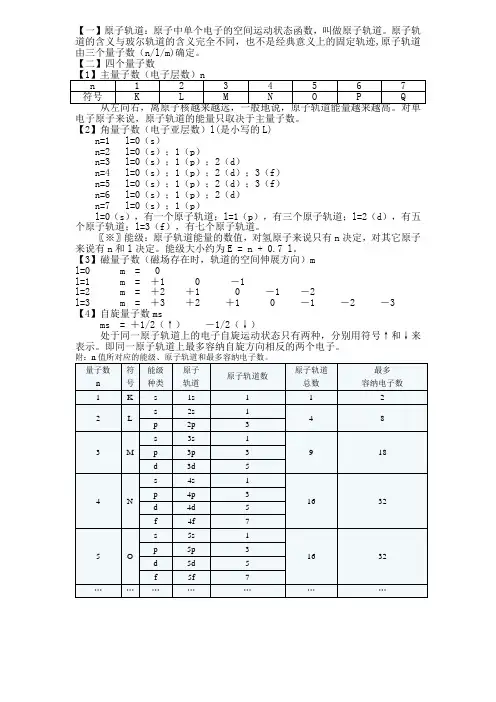
【一】原子轨道：原子中单个电子的空间运动状态函数，叫做原子轨道。

原子轨道的含义与玻尔轨道的含义完全不同，也不是经典意义上的固定轨迹,原子轨道由三个量子数（n/l/m)确定。

【二】四个量子数
电子原子来说，原子轨道的能量只取决于主量子数。

【2】角量子数（电子亚层数）l(是小写的L)
n=1 l=0（s）
n=2 l=0（s）；1（p）
n=3 l=0（s）；1（p）；2（d）
n=4 l=0（s）；1（p）；2（d）；3（f）
n=5 l=0（s）；1（p）；2（d）；3（f）
n=6 l=0（s）；1（p）；2（d）
n=7 l=0（s）；1（p）
l=0（s），有一个原子轨道；l=1（p），有三个原子轨道；l=2（d），有五个原子轨道；l=3（f），有七个原子轨道。

〖※〗能级：原子轨道能量的数值，对氢原子来说只有n决定，对其它原子来说有n和l决定。

能级大小约为E = n + 0.7 l。

【3】磁量子数（磁场存在时，轨道的空间伸展方向）m
l=0 m = 0
l=1 m = ＋1 0 －1
l=2 m = ＋2 ＋1 0 －1 －2
l=3 m = ＋3 ＋2 ＋1 0 －1 －2 －3 【4】自旋量子数ms
ms = ＋1/2（↑）－1/2（↓）
处于同一原子轨道上的电子自旋运动状态只有两种，分别用符号↑和↓来表示。

即同一原子轨道上最多容纳自旋方向相反的两个电子。

原子轨域什么是原子轨域？轨域(Orbitals)和轨道行星环绕太阳运动时，它的运动轨迹是一条明确的路径，这就是所谓的轨道。

在刚开始理解原子的概念时，我们喜欢把原子与太阳系做类比，你可能会想象电子沿着轨道环绕原子核运动。

但这不是事实，事实上电子栖息在被称做轨域的特定空间区域。

轨道和轨域这两词一字之差，但它们的意思十分不同。

明白两者之间的差异很重要。

不可能被画出来的电子运动轨迹为某个东西绘制运动的路径，你必须相对于其运动范围准确的获得它当前的位置信息(比如一个东西要运动1米，而它当前位置信息与实际位置的误差小于0.01米)，并且得到它曾经所在的位置(或它将来所在的位置)。

而对于电子，你做不到这一点。

我们获得一个运动物体位置的最简单方法，就是用眼睛看。

当光子从物体上反射过来，我们获得了物体的位置，但光子同时影响了物体的运动速率及运动方向，由于我们不能精确的得到光子的运动速率和方向，当然也就不能由此推算出其对物体运动所产生的影响。

我们将上文的光子称作测量媒介。

已知的任何测量媒介，当用作测量电子的轨迹时，其对电子运动速率和方向的影响都是显著的，以至于精确的画出电子的运动轨迹事实上是办不到的，我们做的只能是确定电子在某处出现的几率。

海森堡测不准原理不很严谨的版本:你不能同时精确的知道电子(也包括其它粒子)目前的位置和它下一刻的位置。

(原版本:你不能同时获得粒子在某一时刻的精确位置和动量)。

不能为电子绘制轨道会对我们认识世界造成阻碍吗？不，既然我们办不到某些事情，那么就让我们学会接受并找到其它解决方法。

氢的电子— 1s轨域注意：为了能看清原子核，在下面这张图(以及接下来的轨域图)中，我们将原子核放大了很多倍。

想象一个氢原子，我们在某一瞬间测量出其电子所在的位置并记录。

然后再重复测量并记录一次，你发现电子出现在新的位置上。

但我们并不知道电子是如何从原先的位置跑到现在的位置上的。

a 1s orbital一个1s轨域我们不断重复的测量并记录下电子的位置，在获得足够数据之后，将电子所出现的空间位置逐一在3维模型中标示出，我们发现，一些地方的标注要浓密一些，一些地方的标注要松稀一些。

原子排布规则一、原子排布的基本规则1. 能量最低原理- 原子的电子排布遵循能量最低原理，即电子在原子轨道上的分布要尽可能使整个原子的能量处于最低状态。

- 在多电子原子中，电子的能量不仅取决于主量子数n，还与角量子数l有关。

一般来说，n + l值越大，电子的能量越高。

当n相同时，l越大，能量越高，例如E_{ns}<E_{np}<E_{nd}<E_{nf}。

2. 泡利不相容原理- 每个原子轨道最多只能容纳两个电子，且这两个电子的自旋方向必须相反。

- 例如，在1s轨道中，最多只能容纳2个电子，一个电子的自旋量子数m_s = +(1)/(2)，另一个电子的自旋量子数m_s=-(1)/(2)。

3. 洪特规则- 电子在能量相同的轨道（简并轨道）上排布时，总是尽可能分占不同的轨道且自旋方向相同。

- 例如，碳（C）原子的电子排布式为1s^22s^22p^2，这两个2p电子会分占两个不同的2p轨道（2p_x和2p_y或其他组合），且自旋方向相同。

- 洪特规则的特例：对于能量相同的轨道，当电子排布为全充满（p^6、d^10、f^14）、半充满（p^3、d^5、f^7）、全空（p^0、d^0、f^0）时，原子的能量较低，状态较稳定。

例如，铬（Cr）原子的电子排布式为[Ar]3d^54s^1，而不是[Ar]3d^44s^2，因为3d^5是半充满状态，更稳定；铜（Cu）原子的电子排布式为[Ar]3d^104s^1，而不是[Ar]3d^94s^2，因为3d^10是全充满状态，更稳定。

二、电子层与原子轨道1. 电子层（主量子数n）- 电子层用主量子数n = 1,2,3,·s表示，n值越大，表示电子离核越远，能量越高。

- n = 1时为K层，n = 2时为L层，n = 3时为M层，以此类推。

2. 原子轨道类型（角量子数l）- 对于确定的n值，l = 0,1,·s,n - 1。

- 当l = 0时，原子轨道为s轨道，呈球形对称；当l = 1时，原子轨道为p轨道，呈哑铃形，有p_x、p_y、p_z三个等价轨道；当l = 2时，原子轨道为d轨道，形状较为复杂；当l = 3时，原子轨道为f轨道，形状更复杂。

原子轨道的界面图名词解释一、引言在化学和物理学领域中，原子轨道是描述电子在原子核周围运动的概念。

为了更好地理解和描述原子轨道的性质，科学家们通常使用界面图来进行解释和表达。

本文将从不同角度解释和解读原子轨道的界面图，以帮助读者更好地理解和掌握这一概念。

二、原子轨道的基本概念原子轨道是描述电子在原子核周围运动的概念。

根据量子力学的原理，电子具有波粒二象性，因此其运动状态可以用波函数来描述。

原子轨道实际上就是电子波函数的空间分布图，它可以预测电子在不同能级和位置上的分布情况。

三、界面图的概念及作用界面图是将原子轨道的波函数以图像的形式表示出来的工具。

它可以帮助我们更直观地理解和观察电子的运动状态和行为。

在界面图中，波函数的大小和符号用颜色的深浅和正负表示，从而展示出电子在不同位置上的概率分布。

四、s轨道的界面图s轨道是最简单的一种原子轨道，它具有球对称的空间分布。

在界面图中，s轨道通常以一个球状的云团来表示，其大小代表了电子在该位置上的概率。

s轨道一般呈现出均匀的概率分布，电子在轨道内的各个点上的概率都相等。

五、p轨道的界面图p轨道是具有双球对称的原子轨道，它包括三个不同方向上的轨道，分别表示为px、py和pz轨道。

在界面图中，p轨道通常以两个球状的云团来表示，分别代表了电子分布在不同方向上的概率。

每个p轨道都有一个主轴，沿着该轴电子的概率分布最大。

六、d轨道的界面图d轨道是具有复杂形状的原子轨道，它包括五个不同方向上的轨道，分别表示为dxy、dyz、dxz、dx2-y2和dz2轨道。

在界面图中，d轨道的形状常常被描述为带有不规则节点的云团。

这些节点将电子的概率分布切割成了不同的区域，表现出d轨道的复杂性。

七、界面图的应用界面图不仅能够用于表达和理解原子轨道的性质，还可以在化学反应和分子结构研究中发挥重要作用。

通过观察和分析界面图，化学家们可以预测不同原子或分子之间的相互作用及反应过程。

界面图的应用范围广泛，为化学领域的研究提供了重要的工具和思路。

原子轨道系数
原子轨道系数是描述电子在原子中运动的概率分布的数值。

这些数值用来构建分子轨
道和描述分子结构的性质。

由于原子轨道系数是基于量子力学的计算结果，因此不能直接
使用真实的名字或引用。

以下是一份示例的原子轨道系数表：
原子序数：1
电子组态：1s²
轨道系数：0.3605, 0.3201
原子序数：2
电子组态：1s²2s²
轨道系数：0.214, 0.193
原子序数：3
电子组态：1s²2s²2p⁶
轨道系数：0.2255, 0.2028, 0.2028, 0.2028, 0.2028, 0.2028
请注意，这只是一个示例，轨道系数的数值和组态可能会随着具体的原子而有所不同。

真实的原子轨道系数通过计算或实验来确定，而这里提供的数值仅用于演示目的。